二次函数+圆+相似

专题：二次函数+圆+相似 \(\qquad \qquad \qquad \qquad\) 难度系数：★★★★

 

【题目】

如图，已知抛物线\(y=ax^2+bx+c(ac<0)\)与\(x\)轴交于\(A\)、\(B\)（\(A\)在\(B\)的左边），与\(y\)轴交于\(C\)，且\(OB=4OA\)．

(1)若点\(A\)的坐标是\((-1,0)\)，\(C\)的坐标是\((0,-4)\)，试求抛物线的解析式；
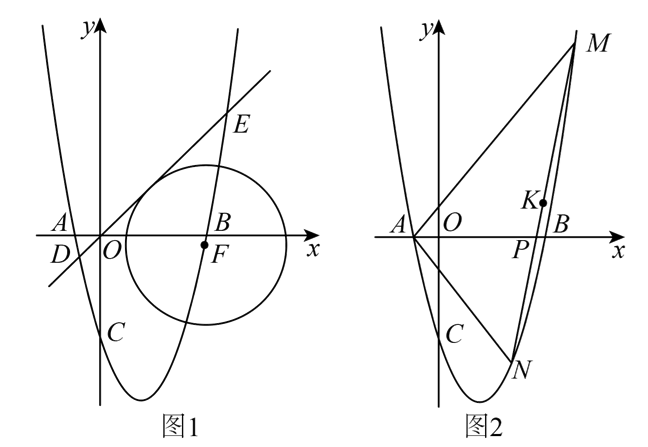
(2)在（1）的条件下，如图1，直线\(y=x\)与抛物线\(y=ax^2+bx+c\)交于\(D\)、\(E\)两点，点\(F\)在直线\(DE\)下方的抛物线上，若以\(F\)为圆心作\(⊙F\)，满足\(⊙F\)与直线\(DE\)相切，求当\(⊙F\)的半径最大时，点\(F\)的坐标；
(3)如图2，若\(OB=OC\)，\(M、N\)分别是抛物线对称轴右侧上的两点（\(M\)在\(N\)的右边），连接\(AM、AN、MN，MN\)交\(x\)轴于点\(P\)，点\(K\)是\(MN\)的中点，若\(△ANM\)的内心在\(x\)轴上，\(K\)的纵坐标为\(n\)，试探究的值是否为定值，若是，求出这个定值；若不是，请说明理由．
 
 
 
 
 

【详解】

第一问： 抛物线的解析式为\(y=x^2-3x-4\)；（待定系数法，过程略）
 

第二问： 【思考痕迹】
方法1 ： 如图一，过点\(F\)作\(FH⊥DE\)，因为\(⊙F\)与直线\(DE\)相切，所以由于\(DE\)是确定，\(FH\)取到最大值时\(S_{ΔDEF}\)最大，此时可考虑“铅垂法”求点\(F\)的坐标.
 

方法2： 如图二，过点\(F\)作\(FQ||y\)轴，由于直线\(DE：y=x\)，所以直线\(DE\)与\(x\)轴坐标轴的夹角为\(45^\circ\)，易得\(∆QFH\)是等腰直角三角形，则\(QF\)取到最大时\(FH\)取到最大值.（在初中里，要多留意一些特殊角\(30^\circ\)、$45^\circ $、$60^\circ $）

 

【解】 如图，过\(F\)作\(FH⊥DE\)于\(H\)，过\(F\)作\(FQ∥y\)轴，交直线\(DE\)于\(Q\)，

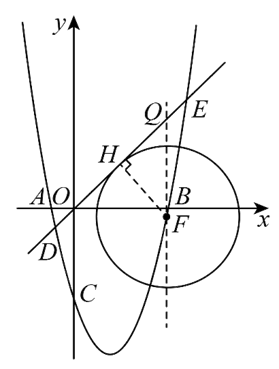
\(∵ DE\)为\(⊙F\)的切线，\(∴H\)在\(⊙F\)上，\(r=HF\)，
\(∵\)直线\(y=x\)，\(∴ ∠HOF=45^\circ\)，\(∴ QF=\sqrt{2}HF=\sqrt{2}r\)，
设\(Q(m,m)\)，\(F(m,m^2-3m-4)\)，
\(∴ QF=-m^2+4m+4=-(m-2)^2+8\)，
\(∵-1<0\)，\(∴\)当\(m=2\)时，\(QH_{max}=8\)，
\(∴ r_{max}=4\sqrt{2}\)，
\(∴y_F=2^2-3×2-4=-6\)，
\(∴F(2,-6)\)；
 

第三问： 【思考痕迹】
分析已知条件
（1）\(OB=OC\)，\(OB=4OA\)

用于求二次函数解析式，设\(A(-m,0)\)，则\(B(4m,0)\)，\(C(0,-4m)\)，易得二次函数解析式\(y=\dfrac{1}{m} x^2-3x-4m\).
（解析式求不出来，若\(\dfrac{PB}{n}\)的值为定值，即\(\dfrac{PB}{n}\)的值与\(m\)的取值无关）
（2）点\(K\)是\(MN\)的中点，\(K\)的纵坐标为\(n \)

由中点公式可得\(y_M+y_N=2n\).
（解题方法假如是代数法，条件中的中点往往想到两个点的中点公式；假如用几何法，会想到中位线、三线合一等几何性质内容）
（3）\(△ANM\)的内心在\(x\)轴上\(⇒\)想到内心的定义，由该条件易知\(∠MAP=∠NAP⇒\)进而会找相似三角形.
（遇到内心、外心之类的条件，多想到其定义与性质；两个角相等而又不知道角度，常规想到全等三角形或相似三角形等）
 

分析求证
判断\(\dfrac{PB}{n}= \dfrac{2(4m-x_P)}{y_M+y_N}\)是否为定值，用代数法证明要求出点\(P\)的坐标，则要不利用相似求解，要不设直线\(MN：y=kx+t\).则此时要设点\(M(x_1,y_1)\)，\(N(x_2,y_2)\)，变量比较多，计算量较大.

 

【解】
方法1 定值，

设\(A(-m,0)\)，
\(∵ OB=4OA\)，\(OB=OC\)，\(∴ B(4m,0)\)，\(C(0,-4m)\)，
\(∴\)设抛物线解析式为\(y=a(x+m)(x-4m)\)，
将\(C(0,-4m)\)代入得，\(am=1\)，
\(∴\)抛物线解析式为\(y=a(x+m)(x-4m)=\dfrac{1}{m} x^2-3x-4m\)，
设直线\(MN：y=kx+t\)，\(M(x_1,y_1)\)，\(N(x_2,y_2)\)，

此时\(P(-\dfrac{t}{k},0)\).
联立\(\left\{ \begin{array}{c} y=kx+t\\ y=\dfrac{1}{m} x^2-3x-4m \end{array} \right. \)得到\(\dfrac{1}{m} x^2-(3+k)x-4m-t=0\)，
（在运算过程中遇到式子\(x_1+x_2\)、\(x_1 x_2\)、\(y_1+y_2\)会想到韦达定理，则用到联立方程）
则\(x_1+x_2=3m+km\)，\(x_1 x_2=-4mt^2-mt\)，
\(∵\)点\(K\)是\(MN\)的中点，

\(∴\)\(n=\dfrac{y_1+y_2}{2}=\dfrac{k(x_1+x_2 )+2t}{2}=\dfrac{mk^2+3mk+2t}{2}\)，
\(∴\dfrac{BP}{n}=\dfrac{4m+\dfrac{t}{k}}{n}=\dfrac{8mk+2t}{mk^3+3mk^2+2tk}\)，
过点\(N\)作\(NI⊥x\)轴，过点\(M\)作\(MT⊥x\)轴，

\(∵△ANM\)的内心在\(x\)轴上，\(∴∠MAP=∠NAP\)，

易得\(△ANI\sim△AMT\)，则\(\dfrac{MT}{NI}=\dfrac{AT}{AI}\)，

即\(\dfrac{y_1}{-y_2}=\dfrac{x_1+m}{x_2+m}⟹\dfrac{kx_1+t}{-kx_1-t}=\dfrac{x_1+m}{x_2+m}⟹2x_1 x_2+(km+t)(x_1+x_2 )+2tm=0\)，
\(∴2k(-4mt^2-mt)+(km+t)(3m+km)+2tm=0\)，
化简得\((t-k)(k-5)=0\)，
\(∴k=5\)或\(k=t\)(舍去)，
\(∴\dfrac{BP}{n}=\dfrac{8mk+2t}{mk^3+3mk^2+2tk}=\dfrac{40m+2t}{200m+10t} =\dfrac{1}{5}\).
 

方法2 定值，
设\(A(-m,0)\)，\(∵ OB=4OA\)，\(OB=OC\)，\(∴ B(4m,0)\)，\(C(0,-4m)\)，
\(∴\)设抛物线解析式为\(y=a(x+m)(x-4m)\)，将\(C(0,-4m)\)代入得，\(am=1\)，
\(∵ △ANM\)的内心在\(x\)轴上，

\(∴ ∠MAB=∠NAB\)，
设直线\(AM\)解析式为：\(y=k(x+m)\)，
联立\(\left\{ \begin{array}{c} y=k(x+m)\\ y=a(x+m)(x-4m) \end{array} \right. \)，解得：\(x_M=mk+4m\)，

（没把二次函数解析式展开，计算简便些）
\(∴ M(mk+4m,mk^2+5mk)\)，
\(∵AP\)平分\(∠MAN\)，且\(P\)在\(x\)轴上，

\(∴\)直线\(AM\)与直线\(AN\)关于\(x\)轴对称，
\(∴\)同理设直线\(AN\)解析式为：\(y=-k(x+m)\)，
（两直线\(l_1\)，\(l_2\)平行，则\(k_1=k_2\)；两直线\(l_1\)，\(l_2\)垂直，则\(k_1 k_2=-1\)；两直线\(l_1\)，\(l_2\)关于\(x\)轴对称，则\(k_1=-k_2\)）
同理可求出\(N(-mk+4m,mk^2-5mk)\)，
\(∵K\)是\(MN\)的中点，
\(∴x_K=\dfrac{1}{2} (mk+4m-mk+4m)=4m\)，\(y_K=\dfrac{1}{2} (mk^2+5mk+mk^2-5mk)=mk^2\)，
\(∴ K(4m,mk^2 )\)，
设直线\(MN\)解析式为：\(y=k_1 x+b_1\)，

则有\(\left\{ \begin{array}{c} (mk+4m) k_1+b_1=mk^2+5mk\\ (-mk+4m) k_1+b_1=mk^2-5mk \end{array} \right. \)，解得：\(\left\{ \begin{array}{c} k_1=5\\ b_1=mk^2-20m \end{array} \right. \)，

（知道两点坐标可求直线方程）
\(∴\)直线\(MN\)解析式为：\(y=5x+mk^2-20m\)，
当\(y=0\)时，\(5x+mk^2-20m=0\)，解得：\(x=4m-\dfrac{1}{5} mk^2\)，
\(∴ P(4m-\dfrac{1}{5} mk^2,0)\)，\(∴OP=4m-\dfrac{1}{5} mk^2\)，
\(∴PB=OP-OB=4m-(4m-\dfrac{1}{5} mk^2 )=\dfrac{1}{5} mk^2\)，
\(∴ \dfrac{PB}{n}=\dfrac{\dfrac{1}{5} mk^2}{mk^2}=\dfrac{1}{5}\)．
【第三问总结】
1两种解法，都要设元，用其表示各量（线段长度、点坐标等）.
2 联立方程求交点或得到关于\(x\)或\(y\)的韦达定理，也是代数法求解解析几何问题的常规操作.
3 能了解一些高中的知识点或解题方法，也有助于中考题的思考.