25 年湛江一模第 11 题（抽象函数+能成立问题）

专题：函数 \(\qquad \qquad \qquad \qquad\) 题型：抽象函数+能成立问题\(\qquad \qquad \qquad \qquad\) 难度系数：★★★

题目

（25 年湛江一模第 11 题，多选题）定义在\(\mathbf{R}\)上的函数\(f(x)\)和\(g(x)\)，记\(g(x)\)的导函数为\(g^{\prime}(x)\)，且满足\(f(x)+g^{\prime}(x)=4, f(x-1)-g^{\prime}(3-\)\(x)=4\)，若\(g(x)\)为奇函数，则下列结论一定成立的有（ ）
  A．\(f(2)+f(4)=8\) \(\qquad \qquad \qquad \qquad\) B．\(f(2025)=4\)

  C．\(\sum_{n=1}^{2025} f(n)=8100\) \(\qquad \qquad \qquad \qquad\) D．\(g^{\prime}(4)=0\)
 

 

思考痕迹

题目明显是对函数性质的考核，根据已知条件，得到\(f(x)\)和\(g^{\prime}(x)\)的一些基本性质，比如对称性，单调性或周期性等。

知识储备：

1 函数周期性
（1）若\(f(x+a)=f(x+b)\)，则\(y=f(x)\)的周期是\(T=a-b\)．
（2）若\(f(x+a)=-f(x)\)，则\(y=f(x)\)的周期是\(T=2 a\)；
（3）若\(f(x+a)=\dfrac{1}{f(x)}\)，则\(y=f(x)\)的周期是\(T=2 a\)．
2 对称性

若函数\(y=f(x)\)定义域为\(R\)，则两函数\(y=f(x+a)\)与\(y=f(b-x)\)的图象关于直线\(x=\dfrac{b+a}{2}\)对称．
若函数\(y=f(x)\)定义域为\(R\)，则两函数\(y=f(a+x)\)与\(y=c-f(b-x)\)的图象关于点\(\left(\dfrac{b+a}{2}, \dfrac{c}{2}\right)\)对称．

3 综合

若函数\(y=f(x)\)关于直线\(x=a\)对称，关于点\((b, 0)\)对称，则函数\(y=f(x)\)的周期\(T=4|b-a|\).
 
 

解析

由\(f(x)+g^{\prime}(x)=4\)得\(f(x-1)+g^{\prime}(x-1)=4\)．

又\(f(x-1)-g^{\prime}(3-x)=4\)，

所以\(g^{\prime}(x-1)=-g^{\prime}(3-x)\)，即\(g^{\prime}(x)=-g^{\prime}(2-x)\)，

所以\(g^{\prime}(x)\)关于\((1,0)\)对称，\(g^{\prime}(1)=0\)。

（若\(f(x+a)+f(b-x)=c\)，则\(f(x)\)关于\(\left(\dfrac{a+b}{2}, \dfrac{c}{2}\right)\)对称）

又因为\(g(x)\)是奇函数，故\(g^{\prime}(x)\)是偶函数，

（若\(g(x)\)是奇函数，则\(g^{\prime}(x)\)是偶函数；若\(g(x)\)是偶函数，则\(g^{\prime}(x)\)是奇函数）

所以\(g^{\prime}(x)\)满足条件\(g^{\prime}(x+4)=g^{\prime}(x)\)．
（可采取数形结合的方法，把满足条件的大致图象画出，得到其对称性，单调性与周期性等，但不确定最值．）

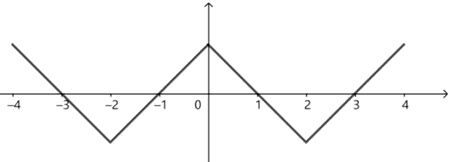
对于选项\(A\)，

因为\(g^{\prime}(4)=-g^{\prime}(-2)=-g^{\prime}(2)\)，所以\(g^{\prime}(4)+g^{\prime}(2)=0\)，

所以\(f(2)+f(4)=4-g^{\prime}(2)+4-g^{\prime}(4)=8-\left[g^{\prime}(4)+g^{\prime}(2)\right]=8\)，

选项\(A\)正确；
\(f(2025)=4-g^{\prime}(2025)=4-g^{\prime}(1)=4\)，选项 \(B\) 正确；

因为\(g^{\prime}(3)=g^{\prime}(-1)=-g^{\prime}(1)=0\)，

所以\(g^{\prime}(1)+g^{\prime}(2)+g^{\prime}(3)+g^{\prime}(4)=0\)，

所以\(\sum_{n=1}^{2025} f(n)=4 \times 2025-\sum_{n=1}^{2225} g^{\prime}(n)=8100-g^{\prime}(2025)=8100-g^{\prime}(1)=8100\)，

选项\(C\)正确；

对于选项 \(D\)，\(g^{\prime}(4)=g^{\prime}(0)\)，但不一定为 0 ，选项\(D\)错误．

故答案为\(A B C\)．