25 年湛江一模第8题(函数奇偶性+恒成立)

专题：概率+数列 \(\qquad \qquad \qquad \qquad\) 题型：马尔可夫链 \(\qquad \qquad \qquad \qquad\) 难度系数：★★★★
 

题目

（2025 年湛江一模第8题） 已知定义在\(\mathbf{R}\)上的函数\(f(x)\)为奇函数，且当\(x>0\)时，\(f(x)=e^{x}-a\)，若\(\forall x \in \mathbf{R}\)，不等式\(f(-x)+f(x-|a-1|) \leqslant 0\)恒成立，则\(a\)的值不可能是（ ）
A．\(-2025\) \(\qquad \qquad \qquad \qquad\) B． \(2025\) \(\qquad \qquad \qquad \qquad\) C．\(e^{2}\) \(\qquad \qquad \qquad \qquad\) D． 3

 
 

思考痕迹

题目明显考核的是函数的奇偶性与单调性，第一个感觉是数形结合，那就要\(a\)的分类讨论，且题中含\(|a-1|\)，故想到分\(a \geq 1\)与\(a<1\)；

当\(a \geq 1\)时，函数图象是左图；当\(a<1\)时，函数图象是右图；
\(\forall x \in \mathbf{R}\)，不等式\(f(-x)+f(x-|a-1|) \leqslant 0\)恒成立
\(\Rightarrow\)即\(f(x-|a-1|) \leqslant-f(-x)=f(x)\)恒成立（不要这就以为函数\(f(x)\)递增）

此时有两种种想法，细看解法．

 
 

解析

方法1函数平移法

若\(a \leqslant 1\)，则函数\(f(x)\)在\(\mathbf{R}\)上单调递增，

又\(x-|a-1| \leqslant x\)，

所以\(f(x-|a-1|) \leqslant f(x)=-f(-x)\)，即\(f(-x)+f(x-|a-1|) \leqslant 0\)恒成立，

故\(a \leqslant 1\)满足题意，故排除选项\(A\)；

若\(a>1\)，则\(a-1>0\)，函数\(f(x)\)在\(\mathbf{R}\)上不单调，图象如图所示，

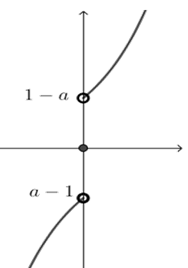
又\(f(-x)+f(x-|a-1|) \leqslant 0\)，即\(f[x-(a-1)] \leqslant f(x)\)，
可理解为函数\(f[x-(a-1)]\)的图象在函数\(f(x)\)的图象下方，
（把函数\(f[x-(a-1)]\)的图象看成由函数\(f(x)\)的图象向右平移\(a-1\)个单位）

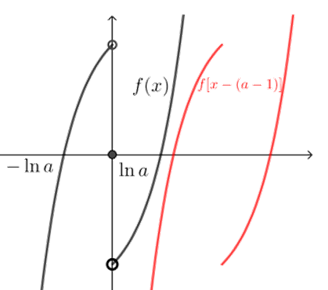
所以\(a-1 \geqslant 2 \ln a\)，即\(2 \ln a-a+1 \leqslant 0\)，

令\(g(a)=2 \ln a-a+1(a>0)\)，

则\(g(2025)=2 \ln 2025-2024<0\)，\(g(3)=2 \ln 3-2=2(\ln 3-1)>0\)
\(g\left(\mathrm{e}^{2}\right)=2 \ln \mathrm{e}^{2}-\mathrm{e}^{2}+1=5-\mathrm{e}^{2}<0\)，

故答案为\(D\)
 
 

方法 2 几何法

当\(a \leqslant 1\)时，如方法 1 ；

当\(a>1\)时，\(\forall x \in \mathbf{R}\)，不等式\(f(-x)+f(x-|a-1|) \leqslant 0\)恒成立
\(\Rightarrow\)即\(f[x-(a-1)] \leq f(x)\)恒成立\((※)\)

该不等式可以理解为任何一\(x\)对应的函数值都大于等于\(x-(a-1)\)对应的函数值，

当\(f(x)>a-1\)或\(f(x)<1-a\)时，显然都成立；

当\(1-a \leq f(x) \leq a-1\)时，如下图，\(A B \| x\)轴（\(A\)是函数在\(y\)轴右侧的一点），

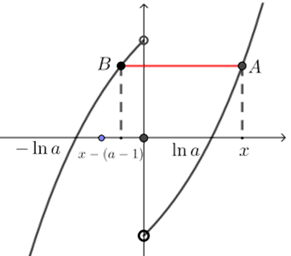
要满足\((※)\)，显然有\(x_{B} \geq x-(a-1)\)，即\(A B \leq a-1\)，

而对于指数型函数是增速越来越快的，故\(A B\)的最小值为\(2 \ln a\)(※），

即\(2 \ln a \leq a-1\)，显然当\(a=3\)时，不能满足不等式，

故答案为\(D\)。
（※ ※）这好像不够严谨，是否能证明呢？

设\(f\left(x_{A}\right)=f\left(x_{B}\right)=k\)，

则\(e^{x_{A}}-a=a-e^{-x_{B}}=k\)，

解得\(x_{A}=\ln (k+a)\)，\(x_{B}=\ln (a-k)\)，

则\(A B=\ln (a-k)-\ln (k+a)=\ln \left(a^{2}-k^{2}\right)\)，

而\(a-1 \leq k \leq 1-a\)，

所以\(a^{2}-k^{2} \leq a^{2}\)，

所以\(A B=\ln \left(a^{2}-k^{2}\right) \leq \ln a^{2}=2 \ln a\)。