5.3.1 (3) 函数的单调性（运用）
${\color{Red}{欢迎到学科网下载资料学习 }}$
[ 【基础过关系列】高二数学同步精品讲义与分层练习(人教A版2019）]
( https://www.zxxk.com/docpack/2875423.html)
\({\color{Red}{ 跟贵哥学数学，so \quad easy！}}\)
选择性第二册同步巩固，难度2颗星！
基础知识
函数单调性与导数
在某个区间\((a ，b)\)内，若\(f'(x)>0\)，则函数\(y=f(x)\)在这个区间内单调递增；
若\(f'(x)<0\) ，则函数\(y=f(x)\)在这个区间内单调递减．
解释
(1) 若函数\(y=f(x)\)在某个区间\((a ，b)\)内单调递增，则\(∀x∈(a ，b)\) ，\(f' (x)≥0\)(含等号)恒成立，但不存在一区间\((c ，d)⊆(a ，b)\)内使得\(f' (x)=0\)；
假如存在一区间\((c ，d)⊆(a ，b)\)内使得\(f' (x)=0\)，那原函数\(y=f(x)\)在区间\((c ，d)\)内恒等于一个常数，即\(f(x)=m\)(\(m\)是个常数)，则原函数不可能在\((a ，b)\)内单调递增.
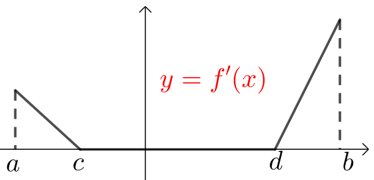\(\qquad \qquad\)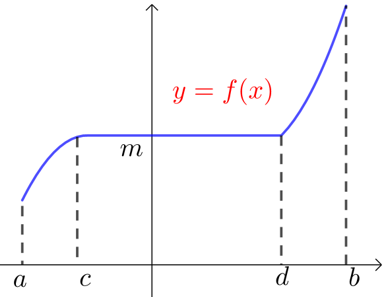 
函数\(y=f(x)\)在某个区间\((a ，b)\)内单调递减有类似结论！
(2)导函数“穿线图”与原函数“趋势图”
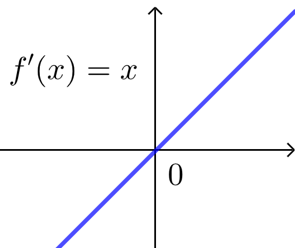
① 导函数“穿线图”关注导函数在各区间的正负，故特别注意函数与x轴的交点情况，
如\(f'(x)=x\)与\(f' (x)=e^x-1\)的“穿线图”视为一样的，它们在\((-∞，0)\)上为负，在\((0，+∞)\)上为正.
\(\qquad \qquad\) 
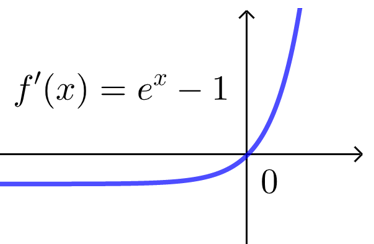
② 原函数“趋势图”仅关注函数在各区间上的单调性，没顾及其最值或曲线形状等，
如由导函数\(f' (x)=x-1\)的“穿线图”易得原函数\(y=f(x)\)在\((-∞，0)\)上递减，在\((0，+∞)\)上为递增，趋势图可如下图，
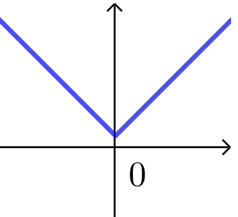
③ 后面涉及到函数单调性均可通过分析导函数“穿线图”得出原函数的单调性.
基本方法
【题型1】已知函数单调性求参数范围
【典题1】 若函数\(f(x)=x^3-3kx+1\)在区间\((1，+∞)\)上单调递增，则实数\(k\)的取值范围是( )
A．\((-∞，1)\) \(\qquad \qquad \qquad\) B．\((-∞，1]\) \(\qquad \qquad \qquad\) C．\([-1，+∞)\) \(\qquad \qquad \qquad\) D．\([1，+∞)\)
解析 因为\(f(x)=x^3-3kx+1\)，所以\(f'(x)=3x^2-3k\)，
当\(k⩽0\)时，\(f'(x)⩾0\)恒成立，\(f(x)\)在\(R\)单调递增，满足题意；
当\(k>0\)时，令\(f'(x)=3x^2-3k⩾0\)，
则 \(x \leqslant-\sqrt{k}\)或\(x⩾\sqrt{k}\)，
因为\(f(x)\)在区间\((1，+∞)\)上单调递增，
所以\(\sqrt{k}⩽1\)，即\(0<k⩽1\)，
综上所述，实数\(k\)的取值范围是\((-∞，1]\)．
故选：\(B\)．
点拨 \(f(x)\)在\((a，b)\)上递增\(⇒f'(x)≥0\)在\((a，b)\)上恒成立，等号是否成立有时需要检验； \(f(x)\)在\((a，b)\)上递减\(⇒f'(x)≤0\)在\((a，b)\)上恒成立，等号是否成立有时需要检验.
【巩固练习】
1.若函数\(f(x)=(x^2-4ax+2) e^x\)在\(R\)上单调递增，则\(a\)的取值范围是\(\underline{\quad \quad}\).
2.已知函数\(f(x)=\sin x+a\cos x\)在区间\(\left(\dfrac{\pi}{4}， \dfrac{\pi}{2}\right)\)上是减函数，则实数\(a\)的取值范围为\(\underline{\quad \quad}\) .
3.已知函数\(f(x)=(x-a)\ln x\)，\(a∈R\)．若函数\(f(x)\)在\((0，+∞)\)上为增函数，则\(a\)的取值范围\(\underline{\quad \quad}\) .
参考答案
-
答案 \(\left[-\dfrac{1}{2}， \dfrac{1}{2}\right]\)
解析 对函数求导：\(f'(x)=(x^2-4ax+2x+2-4a)⋅e^x\)，
由已知有\(f'(x)≥0\)在\(R\)上恒成立，
又因为\(e^x>0\)恒成立，故仅需\(x^2+(2-4a)x+2-4a⩾0\)恒成立，
故\(△=(2-4a)^2-4(2-4a)⩽0\)，解得\(-\dfrac{1}{2} ⩽a⩽\dfrac{1}{2}\) . -
答案 \([1，+∞)\)
解析 由题意得\(f'(x)=\cos x-a\sin x⩽0\)在区间\(\left(\dfrac{\pi}{4}， \dfrac{\pi}{2}\right)\)上恒成立，
所以 \(a \geqslant \dfrac{\cos x}{\sin x}=\dfrac{1}{\tan x}\)在区间\(\left(\dfrac{\pi}{4}， \dfrac{\pi}{2}\right)\)上恒成立，
因为当\(x \in\left(\dfrac{\pi}{4}， \dfrac{\pi}{2}\right)\)时，\(0<\dfrac{1}{\tan x}<1\)，所以\(a⩾1\)． -
答案 \(\left(-\infty，-e^{-2}\right]\)
解析 函数\(f(x)=(x-a)\ln x\)，\(a∈R\)，则\(f^{\prime}(x)=\ln x+1-\dfrac{a}{x}\)，
函数\(f(x)\)在\((0，+∞)\)上为增函数，转化为\(f'(x)⩾0\)在\((0，+∞)\)上恒成立，
即\(a⩽x\ln x+x\)在\((0，+∞)\)上恒成立，
令\(g(x)=x\ln x+x\)，\(x∈(0，+∞)\)，则\(g'(x)=\ln x+2\)，
由\(g'(x)=0\)得\(x=e^{-2}\)，由\(g'(x)>0\)得\(x>e^{-2}\)，由\(g'(x)<0\)得\(0<x<e^{-2}\)，
\(\therefore g(x)\)在\((0，e^{-2})\)上单调递减，在\((e^{-2}，+∞)\)上单调递增，
\(\therefore\)当\(x=e^{-2}\)时，\(g(x)\)取得极小值也是最小值，且\(g(e^{-2})=-e^{-2}\)，
\(\therefore a⩽-e^{-2}\)，
故实数\(a\)的取值范围为\((-∞，-e^{-2}]\).
【题型2】比较大小
【典题1】 若\(1<x<y<2\)，则( )
A．\(e^x+3y<e^y+3x\) \(\qquad \qquad \qquad \qquad \qquad \qquad\) B．\(e^x+3y>e^y+3x\)
C．\(x^3+3y^2<y^3+3x^2\) \(\qquad \qquad \qquad \qquad \qquad \qquad\) D．\(x^3+3y^2>y^3+3x^2\)
解析 令\(f(x)=e^x-3x\)，\(x∈(1，2)\)，
则\(f'(x)=e^x-3\)，由\(f'(x)=0\)，可得\(x=\ln 3\)，
所以当\(x∈(1，\ln 3)\)时，\(f'(x)<0\)，\(f(x)\)单调递减，
当\(x∈(\ln 3，2)\)时，\(f'(x)>0\)，\(f(x)\)单调递增，
所以当\(1<x<y<\ln 3\)时，\(e^x-3x>e^y-3y\)，即\(e^x+3y>e^y+3x\)，
当\(\ln 3<x<y<2\)时，\(e^x-3x<e^y-3y\)，
即\(e^x+3y<e^y+3x\)，故\(A\)，\(B\)错误；
令\(g(x)=x^3-3x^2\)，\(x∈(1，2)\)，
则\(f'(x)=3x^2-6x=3x(x-2)<0\)，
所以\(g(x)\)在\((1，2)\)上单调递减，
因为\(1<x<y<2\)，所以\(x^3+3y^2>y^3+3x^2\)，故\(C\)错误，\(D\)正确．
故选：\(D\)．
点拨 需要根据不等式构造函数，再通过函数单调性判断大小.
【巩固练习】
1.若\(x， y \in\left[-\dfrac{\pi}{2}， \dfrac{\pi}{2}\right]\)，且\(x\sin x-y\sin y>0\)，则下列不等式一定成立的是( )
A．\(x<y\) \(\qquad \qquad \qquad \qquad\) B．\(x>y\) \(\qquad \qquad \qquad \qquad\) C．\(|x|<|y|\) \(\qquad \qquad \qquad \qquad\) D．\(|x|>|y|\)
2.若对于任意的\(0<x_1<x_2<a\)，都有 \(\dfrac{\ln x_1}{x_1}-\dfrac{\ln x_2}{x_2}<\dfrac{1}{x_2}-\dfrac{1}{x_1}\)，则\(a\)的最大值为( )
A．\(2e\) \(\qquad \qquad \qquad \qquad\) B．\(e\) \(\qquad \qquad \qquad \qquad\) C．\(1\) \(\qquad \qquad \qquad \qquad\) D．\(\dfrac{1}{2}\)
3.若\(0<x_1<x_2<1\)，则下列结论正确的是( )
A．\(\ln \dfrac{x_1}{x_2}<e^{x_1}-e^{x_2}\) \(\qquad \qquad \qquad \qquad\) B． \(\ln \dfrac{x_1}{x_2}>e^{x_1}-e^{x_2}\)
C．\(\dfrac{x_1}{x_2}>\sqrt{e^{x_1-x_2}}\) \(\qquad \qquad \qquad \qquad \qquad\) D． \(\dfrac{x_1}{x_2}<\sqrt{e^{x_1-x_2}}\)
参考答案
-
答案 \(D\)
解析 令\(f(x)=x\sin x\)，\(x \in\left[-\dfrac{\pi}{2}， \dfrac{\pi}{2}\right]\)，则\(f(x)\)为偶函数，
当\(x>0\)时，\(f'(x)=\sin x+x\cos x>0\)，即\(f(x)\)在\(\left[0， \dfrac{1}{2} \pi\right]\)上单调递增，
根据偶函数的对称性可知，\(f(x)\)在\(\left[-\dfrac{1}{2} \pi， 0\right)\)上单调递减，距离对称轴越远，函数值越大，
由\(x\sin x-y\sin y>0\)，可得\(x\sin x>y\sin y\)，即\(f(x)>f(y)\)，
从而可得\(|x|>|y|\)．
故选：\(D\)． -
答案 \(C\)
解析 \(\because \dfrac{\ln x_1}{x_1}-\dfrac{\ln x_2}{x_2}<\dfrac{1}{x_2}-\dfrac{1}{x_1}\)，\(\therefore \dfrac{\ln x_1+1}{x_1}<\dfrac{\ln x_2+1}{x_2}\)，
据此可得函数\(f(x)=\dfrac{\ln x+1}{x}\)在定义域\((0，a)\)上单调递增，
其导函数：\(f^{\prime}(x)=\dfrac{1-(\ln x+1)}{x^2}=-\dfrac{\ln x}{x^2} \geq 0\)在\((0，a)\)上恒成立，
据此可得：\(0<x≤1\)，
即实数\(a\)的最大值为\(1\)．
故选：\(C\)． -
答案 \(D\)
解析 对于\(A\)：由\(\ln \dfrac{x_1}{x_2}<e^{x_1}-e^{x_2}\) ，
得\(\ln x_1-\ln x_2<e^{x_1}-e^{x_2}\)，得：\(e^{x_1}-\ln x_1>e^{x_2}-\ln x_2\)，
令\(f(x)=e^x-\ln x\)，则\(f(x_1)>f(x_2)\)，
由函数\(f(x)=e^x-\ln x\)，得：\(f'(x)=e^x-\dfrac{1}{x} \)，\(f'(x)\)在\((0，1)\)递增，
而\(f'(1)=e-1>0\)，\(x→0\)时，\(f'(x)→-∞\)，
故存在\(x_0∈(0，1)\)，使得\(f'(x_0)=0\)，
故\(f(x)\)在\((0，x_0)\)递减，在\((x_0，1)\)递增，
①若\(x_0<x_1<x_2<1\)，则\(f(x_1 )<f(x_2 )\)，
②若\(0<x_1<x_2<x_0\)，则\(f(x_1 )>f(x_2 )\)，
③若\(x_1<x_0<x_2\)，则\(f(x_1 )\)和\(f(x_2 )\)无法比较大小，故\(A\)错误；
同理\(B\)错误；
对于\(C\)：令\(g(x)=x^2 e^x\)，\((0<x<1)\)，
则\(g'(x)=e^x (x^2+2x)>0\)，
故\(g(x)\)在\((0，1)\)递增，由\(0<x_1<x_2<1\)，得\(g(x_1 )<g(x_2 )\)，
即\(x_1^2 e^{x_1}<x_2^2 e^{x_2}\)，即\(\left(\dfrac{x_1}{x_2}\right)^2<\dfrac{e^{x_2}}{e^{x_1}}\)，
故\(\dfrac{x_1}{x_2}<\sqrt{e^{x_2-x_1}}\)，
故\(C\)错误，\(D\)正确；
故选：\(D\)．
【题型3】比较数值大小
【典题1】 若 \(a=\dfrac{\ln 4}{4}\)， \(b=\dfrac{\ln 5.3}{5.3}\)， \(c=\dfrac{\ln 6}{6}\)，则\(a\)、\(b\)、\(c\)的大小是( )
A．\(a<b<c\) \(\qquad \qquad\) B．\(c<b<a\) \(\qquad \qquad\) C．\(c<a<b\) \(\qquad \qquad\) D．\(b<a<c\)
解析 设 \(f(x)=\dfrac{\ln x}{x}\)， \(f^{\prime}(x)=\dfrac{1-\ln x}{x^2}\)，
令\(f'(x)>0\)，可得\(0<x<e\)，令\(f'(x)<0\)，可得\(x>e\)，
所以\(f(x)\)在\((0，e)\)上单调递增，在\((e，+∞)\)上单调递减，
因为\(e<4<5.3<6\)，
所以\(f(4)>f(5.3)>f(6)\)，
即 \(\dfrac{\ln 4}{4}>\dfrac{\ln 5.3}{5.3}>\dfrac{\ln 6}{6}\)，即\(a>b>c\)．
故选：\(B\)．
点拨 需要数值的结构特点构造函数，再通过函数单调性判断大小.
【典题2】 已知 \(a=e^{0.1}-1\)，\(b=\sin 0.1\)，\(c=\ln 1.1\)，则( )
A．\(a<b<c\) \(\qquad \qquad\) B．\(b<c<a\) \(\qquad \qquad\) C．\(c<a<b\) \(\qquad \qquad\) D．\(c<b<a\)
解析 令\(f(x)=e^x-x-1\)，则\(f'(x)=e^x-1\)，
当\(x∈(0，+∞)\)时，\(f'(x)>0\)，故\(f(x)\)在\((0，+∞)\)上是增函数，
故\(f(0.1)>f(0)\)，即 \(e^{0.1}-0.1-1>0\)，故\(a=e^{0.1}-1>0.1\)，
令\(g(x)=\sin x-x\)，则\(g'(x)=\cos x-1<0\)在\((0，1)\)上恒成立，
故\(g(x)=\sin x-x\)在\((0，1)\)上单调递减，
故\(g(0.1)<g(0)\)，即\(\sin 0.1-0.1<0\)，即\(b=\sin 0.1<0.1\)，
令\(h(x)=\ln (x+1)-\sin x\)，
则 \(h^{\prime}(x)=\dfrac{1}{x+1}-\cos x=\dfrac{1-(x+1) \cos x}{x+1}\)，
令\(m(x)=1-(x+1)\cos x\)，
则\(m'(x)=-\cos x+(x+1)\sin x\)，
易知\(m'(x)\)在\(\left(0， \dfrac{\pi}{6}\right)\)上是增函数，
且\(m^{\prime}\left(\dfrac{\pi}{6}\right)=-\dfrac{\sqrt{3}}{2}+\left(1+\dfrac{\pi}{6}\right) \dfrac{1}{2}=\dfrac{-6 \sqrt{3}+6+\pi}{12}<0\)，
故\(m'(x)<0\)在\(\left(0， \dfrac{\pi}{6}\right)\)上恒成立，故\(m(x)\)在\(\left(0， \dfrac{\pi}{6}\right)\)上是减函数，
又\(\because m(0)=1-1=0\)，故\(m(x)<0\)在\(\left(0， \dfrac{\pi}{6}\right)\)上恒成立，
故\(h'(x)<0\)在\(\left(0， \dfrac{\pi}{6}\right)\)上恒成立，故\(h(x)\)在\(\left(0， \dfrac{\pi}{6}\right)\)上是减函数，
故\(h(0.1)<h(0)=0\)，即\(\ln 1.1-\sin 0.1<0\)，即\(c<b\)，
故\(c<b<a\)，
故选：\(D\)．
【巩固练习】
1.已知 \(a=\dfrac{\ln \sqrt{2}}{4}\)， \(b=\dfrac{1}{e^2}\)， \(c=\dfrac{\ln \pi}{2 \pi}\)，则\(a\)、\(b\)、\(c\)的大小关系为( )
A.\(a<c<b\) \(\qquad \qquad\) B. \(b<a<c\) \(\qquad \qquad\) C. \(a<b<c\) \(\qquad \qquad\) D. \(c<a<b\)
2.已知\(a=\dfrac{3}{\ln 3}\)，\(b=e\)， \(c=\dfrac{e^2}{2}\)(\(e\)为然对数的底数)，则\(a\)、\(b\)、\(c\)的大小关系为( )
A．\(c>a>b\) \(\qquad \qquad\) B．\(c>b>a\) \(\qquad \qquad\) C．\(a>c>b\) \(\qquad \qquad\) D．\(b>c>a\)
3.设\(a=e^{-1}\) ， \(b=\dfrac{1}{2} e^{-\frac{1}{2}}\)，\(c=\ln 2\)，则\(a\)、\(b\)、\(c\)的大小关系为( )
A.\(b<c<a\) \(\qquad \qquad\) B.\(a<b<c\) \(\qquad \qquad\) C. \(b<a<c\) \(\qquad \qquad\) D. \(c<a<b\)
4.设 \(a=\dfrac{10}{11}\)， \(b=\dfrac{1}{e^{0.1}}\)，\(c=0.9\)，则( )
A．\(c<b<a\) \(\qquad \qquad\) B．\(c<a<b\) \(\qquad \qquad\) C．\(b<c<a\) \(\qquad \qquad\) D．\(a<c<b\)
参考答案
-
答案 \(C\)
解析 因为\(a=\dfrac{\ln \sqrt{2}}{4}=\dfrac{\ln 2}{8}=\dfrac{2 \ln 2}{16}=\dfrac{\ln 4}{16}\)，\(b=\dfrac{1}{e^2}=\dfrac{\ln e}{e^2}\)，\(c=\dfrac{\ln \pi}{2 \pi}=\dfrac{\ln \sqrt{\pi}}{\pi}\)，
所以构造函数 \(f(x)=\dfrac{\ln x}{x^2}\)，
则 \(f^{\prime}(x)=\dfrac{x-2 x \ln x}{x^4}=\dfrac{1-2 \ln x}{x^3}\)，
令\(f'(x)>0\)得\(0<x<\sqrt{e}\)；令\(f'(x)<0\)得\(x>\sqrt{e}\)；
所以函数\(f(x)\)在\((0，\sqrt{e})\)上单调递增，在\((\sqrt{e}，+∞)\)上单调递减，
因为\(\sqrt{e}<\sqrt{\pi}<e<4\)，
所以\(f(\sqrt{\pi})>f(e)>f(4)\)，即\(c>b>a\).
故选：\(C\)． -
答案 \(A\)
解析 \(\because a=\dfrac{3}{\ln 3}\)， \(b=e=\dfrac{e}{\ln e}\)， \(c=\dfrac{e^2}{2}=\dfrac{e^2}{\ln e^2}\)，
\(\therefore\)令\(f(x)=\dfrac{x}{\ln x}\)，则 \(f^{\prime}(x)=\dfrac{\ln x-1}{(\ln x)^2}\)，
\(\therefore\)当\(x∈(e，+∞)\)时，\(f'(x)>0\)，
\(\therefore f(x)\)在\([e，+∞)\)上是增函数，
而\(a=\dfrac{3}{\ln 3}=f(3)\)，\(b=e=\dfrac{e}{\ln e}=f(\mathrm{e})\)，\(c=\dfrac{e^2}{2}=\dfrac{e^2}{\ln e^2}=f\left(e^2\right)\)，
且\(e<3<e^2\)，则\(c>a>b\)，
故选：\(A\)． -
答案 \(C\)
解析 设\(\text { 没 } f(x)=x e^{-x}\) ，则 \(f^{\prime}(x)=(1-x) e^{-x}\)，
当\(x≤1\)时，\(f'(x)≥0\)，\(f(x)\)单调递增，
当\(x>1\)时，\(f'(x)<0\)，\(f(x)\)单调递减，
\(\therefore f(1)>f(\dfrac{1}{2} )\)，即\(a>b\)，
\(\because c=\ln 2>\ln \sqrt{e}=\dfrac{1}{2}>\dfrac{1}{e}=a\)，\(\therefore b<a<c\)，
故选：\(C\)． -
答案 \(A\)
解析 令\(f(x)=e^x-(x+1)\)，则\(f'(x)=e^x-1\)，
当\(x>0\)时，\(f'(x)>0\)，当\(x<0\)时，\(f'(x)<0\)，
\(\therefore\)当\(x=0\)时，\(f(x)\)取得最小值，即\(f(x)⩾f(0)=0\)，
\(\therefore e^x⩾x+1\)，\(\therefore e^{0.1}>0.1+1=1.1\)，
\(\therefore \dfrac{1}{e^{0.1}}<\dfrac{1}{1.1}=\dfrac{10}{11}\)，即\(b<a\)，
\(\therefore \dfrac{1}{e^{0.1}}=e^{-0.1}>-0.1+1=0.9\)，即\(b>c\)，
综上，可得\(c<b<a\)．
故选：\(A\)．
分层练习
【A组---基础题】
1.已知函数\(f(x)=(x^2-4x+a) e^x\)在区间\([-2，3]\)上单调递减，则实数\(a\)的取值范围是( )
A．\((-∞，-4]\) \(\qquad \qquad\) B．\((-∞，5]\) \(\qquad \qquad\) C．\((-∞，1]\) \(\qquad \qquad\) D．\((-∞，-8]\)
2.已知\(a=\dfrac{\ln 3}{3}\)，\(b=\dfrac{1}{e}\)，\(c=\dfrac{\ln 5}{5}\)，则以下不等式正确的是( )
A．\(c>b>a\) \(\qquad \qquad\) B．\(a>b>c\) \(\qquad \qquad\) C．\(b>a>c\) \(\qquad \ \qquad\) D．\(b>c>a\)
3.已知\(a=\dfrac{1}{e}\)，\(b=\dfrac{\ln 5}{5}\)，\(c=\dfrac{2}{5}\)，则\(a\)、\(b\)、\(c\)的大小关系为( )
A．\(b<c<a\)\(\qquad \qquad\) B．\(c<a<b\) \(\qquad \qquad\) C．\(c<b<a\) \(\qquad \qquad\) D．\(b<a<c\)
4.下列不等式正确的是( )
A．\(\dfrac{\ln 2}{2}>\dfrac{\ln 4}{4}\) \(\qquad \qquad\) B．\(\dfrac{2 \ln 3}{3}>\ln 2\) \(\qquad \qquad\) C．\(e\ln 10>10\) \(\qquad \qquad\) D． \(2^{\sqrt{6}}>6\)
5.设\(a=e^{0.5}\)，\(b=\dfrac{3}{e}\)，\(c=\ln 3\)，其中\(e\)为自然对数的底数，则\(a\)、\(b\)、\(c\)的大小关系是( )
A.\(c<a<b\) \(\qquad \qquad\) B. \(b<c<a\) \(\qquad \qquad\) C. \(a<c<b\) \(\qquad \qquad\) D. \(c<b<a\)
6.已知\(a=\ln \sqrt[3]{3}\)，\(b=e^{-1}\)，\(c=\ln (e+1)-1\)，则( )
A.\(a<b<c\) \(\qquad \qquad\) B. \(c<a<b\) \(\qquad \qquad\) C. \(a<c<b\) \(\qquad \qquad\) D. \(b<c<a\)
7.若\(\ln x-\ln y<\dfrac{1}{\ln x}-\dfrac{1}{\ln y}(x>1， y>1)\)，则( )
A． \(e^{y-x}>1\) \(\qquad \qquad\) B． \(e^{y-x}<1\) \(\qquad \qquad\) C． \(e^{y-x-1}>1\) \(\qquad \qquad\) D． \(e^{y-x-1}<1\)
8.若\(\alpha， \beta \in\left[-\dfrac{\pi}{2}， \dfrac{\pi}{2}\right]\)，且\(α\sin α-β\sin β>\cos α-\cos β\)，则下列结论中必定成立的是( )
A．\(α>β\) \(\qquad \qquad \qquad\) B．\(α>-β\) \(\qquad \qquad \qquad\) C．\(α<β\) \(\qquad \qquad \qquad\) D．\(|α|>|β|\)
9.已知 \(0<\alpha<\beta<\dfrac{\pi}{2}\)，则下列不等式中恒成立的是( )
A．\(α^α<β^β\)\(\qquad \qquad \qquad\) B．\(α^α≤β^β\) \(\qquad \qquad \qquad\) C．\(α^β>β^α\) \(\qquad \qquad \qquad\) D．\(α^β<β^α\)
10.已知函数\(f(x)=\dfrac{1}{2} x^2+2ax-\ln x\)，若\(f(x)\)在区间\([1，3]\)上单调递增，则实数\(a\)的范围为\(\underline{\quad \quad}\) .
参考答案
-
答案 \(A\)
解析 因为函数\(f(x)=(x^2-4x+a) e^x\)在\([-2，3]\)上单调递减，
所以\(f'(x)=(x^2-2x+a-4) e^x⩽0\)在\([-2，3]\)上恒成立，
则\(x^2-2x+a-4⩽0\)在\([-2，3]\)上恒成立，
即\(a \leqslant\left(-x^2+2 x+4\right)_{\text {min }}\)，
又\(-x^2+2x+4\)的最小值为\(-4\)，所以\(a⩽-4\)，
故选：\(A\)． -
答案 \(C\)
解析 令 \(f(x)=\dfrac{\ln x}{x}\)，则 \(f^{\prime}(x)=\dfrac{1-\ln x}{x^2}\)，
当\(x>e\)时，\(f'(x)<0\)，函数单调递减，
因为\(5>3>e\)，所以\(f(5)<f(3)<f(e)\)，
即 \(\dfrac{\ln 5}{5}<\dfrac{\ln 3}{3}<\dfrac{\ln e}{e}\)，即\(b>a>c\)．
故选：\(C\)． -
答案 \(D\)
解析 \(\because a-c=\dfrac{1}{e}-\dfrac{2}{5}=\dfrac{5-2 e}{5 e}<0\)，\(\therefore a<c\)，
令 \(f(x)=\dfrac{\ln x}{x}\)，则\(f^{\prime}(x)=\dfrac{1-\ln x}{x^2}\)，
故当\(x∈(e，+∞)\)时， \(f^{\prime}(x)=\dfrac{1-\ln x}{x^2}<0\)，
故\(f(x)\)在\([e，+∞)\)上是减函数，
而 \(a=\dfrac{1}{e}=f(\mathrm{e})\)， \(b=\dfrac{\ln 5}{5}=f(5)\)，
故\(b<a\)，故\(b<a<c\)，
故选：\(D\)． -
答案 \(B\)
解析 因为 \(\dfrac{\ln 4}{4}=\dfrac{2 \ln 2}{4}=\dfrac{\ln 2}{2}\)，\(A\)错误；
\(2\ln 3=\ln 9\)，\(3\ln 2=\ln 8\)，\(\ln 9>\ln 8\)，故\(2\ln 3>3\ln 2\)，
所以 \(\dfrac{2 \ln 3}{3}>\ln 2\)，\(B\)正确；
令 \(f(x)=\dfrac{\ln x}{x}\)，则 \(f^{\prime}(x)=\dfrac{1-\ln x}{x^2}\)，
易得，当\(0<x<e\)时，\(f'(x)>0\)，函数单调递增，
当\(x>e\)时，\(f'(x)<0\)，函数单调递减，
故\(f(10)<f(e)\)，
所以 \(\dfrac{\ln 10}{10}<\dfrac{1}{e}\)，即\(e\ln 10<10\)，\(C\)错误；
根据二次函数与幂函数性质可知，当\(2<x<4\)时，\(2^x<x^2\)，
所以 \(2^{\sqrt{6}}<\sqrt{6}^2=6\)，\(D\)错误．
故选：\(B\)． -
答案 \(D\)
解析 易知\(a=e^{0.5}>\left(\dfrac{9}{4}\right)^{0.5}=1.5\)，\(b=\dfrac{3}{e}<\dfrac{3}{2}=1.5\)，\(c=\ln 3<\ln \sqrt{e^3}=1.5\)，
令\(f(x)=\ln x-\dfrac{x}{e}\)，则\(f^{\prime}(x)=\dfrac{1}{x}-\dfrac{1}{e}\)，
故当\(x∈(e，+∞)\)时，\(f'(x)<0\)，
故\(f(x)\)在\((e，+∞)\)上是减函数，
而\(f(e)=0\)，故\(f(3)<0\)，
即\(\ln 3-\dfrac{3}{e}<0\)，即 \(\ln 3<\dfrac{3}{e}\)，
故\(c<b<a\)，
故选：\(D\)． -
答案 \(B\)
解析 令 \(f(x)=\dfrac{\ln x}{x}(x \geq e)\)，
则\(f^{\prime}(x)=\dfrac{1-\ln x}{x^2}<0\)，即\(f(x)\)在\([e，+∞)\)上单调递减，
所以\(a=\ln \sqrt[3]{3}=\dfrac{1}{3} \ln 3=f(3)\)，\(b=e^{-1}=\dfrac{1}{e}=f(e)\)，所以\(a<b\)，
因为\(c=\ln (e+1)-1=\ln \dfrac{e+1}{e}=\ln \left(1+\dfrac{1}{e}\right)\)，
因为\(\sqrt[3]{3}>1+\dfrac{1}{e}\)，所以 \(\ln \sqrt[3]{3}>\ln \left(1+\dfrac{1}{e}\right)\)，即\(a>c\)，
综上，\(b>a>c\).
故选：\(B\)． -
答案 \(A\)
解析 依题意， \(\ln x-\dfrac{1}{\ln x}<\ln y-\dfrac{1}{\ln y}\)，
令\(f(t)=t-\dfrac{1}{t}\)，则 \(f^{\prime}(t)=1+\dfrac{1}{t^2}>0\)，
\(\therefore\)函数\(f(t)\)在\(R\)上单调递增，
\(\because \ln x-\dfrac{1}{\ln x}<\ln y-\dfrac{1}{\ln y}\)，即 \(f(\ln x)<f(\ln y)\)，
\(\therefore \ln x<\ln y\)，
\(\therefore 1<x<y\)，
\(\therefore y-x>0\)，
\(\therefore e^{y-x}>e^0=1\)．
故选：\(A\)． -
答案 \(D\)
解析 不等式\(α\sin α-β\sin β>\cos α-\cos β\)，可整理为\(α\sin α-\cos α>β\sin β-\cos β\)，
令\(f(x)=x\sin x-\cos x\)， \(x \in\left[-\dfrac{\pi}{2}， \dfrac{\pi}{2}\right]\)，
上述不等式等价于\(f(α)>f(β)\)，
\(\because f(-x)=(-x)\sin (-x)-\cos (-x)=x\sin x-\cos x=f(x)\)，
\(\therefore f(x)\)为偶函数．
又\(f'(x)=2\sin x+x\cos x\)，
\(\therefore\)当\(0<x≤\dfrac{\pi}{2} \)时，\(\sin x>0\)，\(x\cos x≥0\)，\(\therefore f'(x)>0\)，
\(\therefore f(x)\)在 \(\left(0， \dfrac{\pi}{2}\right]\)上单调递增，在 \(\left[-\dfrac{\pi}{2}， 0\right)\)上单调递减．
结合\(f(x)\)的单调性和奇偶性可作出函数\(f(x)\)的大致草图如下：
\(\because f(α)>f(β)\)， \(\therefore |α|>|β|\)．
故选：\(D\)． -
答案 \(D\)
解析 构造函数 \(f(x)=\dfrac{\ln x}{x}\)，则 \(f^{\prime}(x)=\dfrac{1-\ln x}{x}\)，
令\(f'(x)>0\)，解得\(0<x<e\)，令\(f'(x)<0\)，解得\(x>e\)，
\(\therefore\)函数\(f(x)\)在(0，e)上单调递增，在(e，+∞)上单调递减，
\(\therefore\)函数\(f(x)\)在 \(\left(0， \dfrac{\pi}{2}\right)\)上单调递增，
\(\therefore f(α)<f(β)\)，即 \(\dfrac{\ln \alpha}{\alpha}<\dfrac{\ln \beta}{\beta}\)，
\(\therefore β\ln α<α\ln β\)，即\(\ln α^β<\ln β^α\)，
\(\therefore α^β<β^α\)，
故选：\(D\)． -
答案 \([0，+∞)\)
解析 由题意知，\(f'(x)=x+2a-\dfrac{1}{x} ⩾0\)在\([1，3]\)上恒成立，
即\(2a⩾\dfrac{1}{x} -x\)，
又函数\(y=\dfrac{1}{x} -x\)在\([1，3]\)上单调递减，
所以当\(x=1\)时，函数\(y\)取得最大值，为\(0\)，
所以\(2a≥0\)，即\(a≥0\)．
【B组---提高题】
1.若\(x，y∈(0，+∞)\)，\(x+\ln x=e^y+\sin y\)，则( )
A．\(\ln (x-y)<0\) \(\qquad \qquad\) B．\(\ln (y-x)>0\) \(\qquad \qquad\) C．\(x<e^y\) \(\qquad \qquad\) D．\(y<\ln x\)
2.已知\(a=8^{10}\)，\(b=9^9\)，\(c=10^8\)，则\(a\)，\(b\)，\(c\)的大小关系为( )
A．\(b>c>a\) \(\qquad \qquad\) B．\(b>a>c\) \(\qquad \qquad\) C．\(a>c>b\) \(\qquad \qquad\) D．\(a>b>c\)
参考答案
-
答案 \(C\)
解析 设\(f(x)=x-\sin x(x>0)\)，则\(f'(x)=1-\cos x⩾0\)(不恒为零)，
故\(f(x)\)在\((0，+∞)\)上为增函数，故\(f(x)>f(0)=0\)，
所以\(x>\sin x\)，故\(y>\sin y\)在\((0，+∞)\)上恒成立，
所以\(x+\ln x<e^y+y=e^y+\ln e^y\)，
但\(g(x)=x+\ln x\)为\((0，+∞)\)上的增函数，
故\(x<e^y\)，即\(\ln x<y\)，
所以\(C\)成立，\(D\)错误．
取\(x=e\)，考虑\(1+e=e^y+\sin y\)的解，若\(y⩾e+1\)，
则\(e^y⩾e^{e+1}>5>e+2⩾1+e-\sin y\)，矛盾，
故\(y<e+1\)，即\(y-x<1\)，
此时\(\ln (y-x)<0\)，故\(B\)错误．
取\(y=1\)，考虑\(x+\ln x=e+\sin 1\)，
若\(x⩽2\)，则\(x+\ln x⩽2+\ln 2<3<e+\dfrac{1}{2}<e+\sin 1\)，矛盾，
故\(x>2\)，此时\(x-y>1\)，此时\(\ln (x-y)>0\)，故\(A\)错误，
故选：\(C\)． -
答案 \(D\)
解析 令\(f(x)=(18-x)\ln x\)，
则\(f^{\prime}(x)=-\ln x+\dfrac{18}{x}-1\)在\(x⩾8\)时单调递减，
又\(f^{\prime}(8)=\dfrac{5}{4}-\ln 8<\dfrac{5}{4}-\ln e^2<0\)，
所以\(f'(x)<0\)在\(x⩾8\)时恒成立，
故\(f(x)\)在\(x⩾8\)时单调递减，所以\(f(8)>f(9)>f(10)\)．
所以\(10\ln 8>9\ln 9>8\ln 10\)，故 \(8^{10}>9^9>10^8\)．
故\(a>b>c\)．
故选：\(D\)．
【C组---拓展题】
1.若 \(x+\dfrac{3}{2} y-2=e^x+3 \ln \dfrac{y}{2}\)，其中\(x>2\)，\(y>2\)，则( )
A．\(e^x<y\) \(\qquad \qquad\) B．\(2x>y\) \(\qquad \qquad\) C． \(4 e^{\frac{x}{2}}>y\) \(\qquad \qquad\) D．\(2e^x>y\)
2.若实数\(a\)，\(b\)满足 \(2 \ln a+\ln (2 b) \geq \dfrac{a^2}{2}+4 b-2\)，则( )
A．\(a+b=\sqrt{2}+\dfrac{1}{4}\) \(\qquad \qquad\) B．\(a-2b=\sqrt{2}-\dfrac{1}{4} \) \(\qquad \qquad\) C．\(a^2+b>3\) \(\qquad \qquad\) D．\(a^2-4b<1\)
参考答案
-
答案 \(D\)
解析 因为 \(x+\dfrac{3}{2} y-2=e^x+3 \ln \dfrac{y}{2}\)，
所以 \(e^x-x=\dfrac{3}{2} y-2-3 \ln \dfrac{y}{2}=2\left(\dfrac{y}{2}-1-\ln \dfrac{y}{2}\right)+\dfrac{y}{2}-\ln \dfrac{y}{2}\)，
令\(f(x)=x-1-\ln x\)，则 \(f^{\prime}(x)=1-\dfrac{1}{x}=\dfrac{x-1}{x}\)，
当\(x>1\)时，\(f'(x)>0\)，\(f(x)\)为增函数，
所以\(f(x)>f(1)=0\)，
因为\(y>2\)，所以 \(\dfrac{y}{2}-1-\ln \dfrac{y}{2}>0\)，
所以 \(e^x-x>\dfrac{y}{2}-\ln \dfrac{y}{2}=e^{\ln \dfrac{y}{2}}-\ln \dfrac{y}{2}\)，\(x>2\)， \(\ln \dfrac{y}{2}>0\)，
令\(g(x)=e^x-x\)，则\(g'(x)=e^x-1\)，
当\(x>0\)时，\(g'(x)>0\)，\(g(x)\)单调递增，
所以 \(\text { 以 } e^x-x>\dfrac{y}{2}-\ln \dfrac{y}{2}=e^{\ln \dfrac{y}{2}}-\ln \dfrac{y}{2}\)，等价于 \(x>\ln \dfrac{y}{2}\)，
所以 \(e^x>\dfrac{y}{2}\)，即\(2e^x>y\)．
故选：\(D\)． -
答案 \(A\)
解析 根据题意，若实数\(a\)，\(b\)满足 \(2 \ln a+\ln (2 b) \geq \dfrac{a^2}{2}+4 b-2\)，
则\(a>0\)且\(b>0\)，
又由 \(\dfrac{a^2}{2}+4 b-2 \geq 2 \times \sqrt{\dfrac{a^2}{2} \times 4 b}-2=2 \sqrt{2 a^2 b}-2\)，当且仅当\(a^2=8b\)时等号成立，
则有 \(2 \ln a+\ln (2 b) \geq 2 \sqrt{2 a^2 b}-2\)，变形可得 \(\ln \left(2 a^2 b\right)-2 \sqrt{2 a^2 b}+2 \geq 0\)，
设 \(g(x)=\ln x-2 \sqrt{x}+2\)，
则其导数 \(g^{\prime}(x)=\dfrac{1}{x}-\dfrac{1}{\sqrt{x}}=\dfrac{1-\sqrt{x}}{x}\)，
当\(0<x≤1\)时，\(g'(x)≥0\)，则\(g(x)\)在区间\((0，1]\)上为增函数，
当\(x≥1\)时，\(g'(x)≤0\)，则\(g(x)\)在区间\([1，+∞)\)上为减函数，
则有\(g(x)≤g(1)=0\)，
若\(\ln \left(2 a^2 b\right)-2 \sqrt{2 a^2 b}+2 \geq 0\)，
即\(g(2a^2 b)≥0\)，必有\(2a^2 b=1\)，
又\(a^2=8b\)，所以\(a=\sqrt{2}\)，\(b=\dfrac{1}{4} \) ，
据此分析选项：对于\(A\)，\(a+b=\sqrt{2}+\dfrac{1}{4} \)，\(A\)正确；
对于\(B\)，\(a-2b=\sqrt{2}-\dfrac{1}{2} \)，\(B\)错误；
对于\(C\)， \(a^2+b=\dfrac{9}{4}\)，\(C\)错误；
对于\(D\)，\(a^2-4b=1\)，\(D\)错误；
故选：\(A\)．
浙公网安备 33010602011771号