5.2.1 三角函数的概念
${\color{Red}{欢迎到学科网下载资料学习 }}$
【基础过关系列】2022-2023学年高一数学上学期同步知识点剖析精品讲义(人教A版2019)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第一册同步巩固,难度2颗星!
基础知识
任意角的三角函数的概念
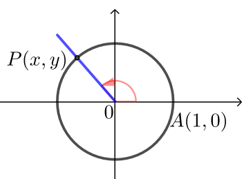
设\(α\)是一个任意角,\(α∈R\),它的终边\(OP\)与单位圆相交于点\(P(x,y)\).
① 把点\(P\)的纵坐标\(y\)叫做\(α\)的正弦函数,记作\(\sinα\),即\(y=\sinα\);
② 把点\(P\)的纵坐标\(x\)叫做\(α\)的余弦函数,记作\(\cosα\),即\(x=\cosα\);
③ 把点\(P\)的纵坐标 \(\dfrac{y}{x}\)叫做\(α\)的正切函数,记作\(\tanα\),即 \(\dfrac{y}{x}=\tan \alpha(x \neq 0)\).
正弦函数\(f(x)=\sin x\),\(x∈R\);余弦函数\(f(x)=\cos x\),\(x∈R\);
正切函数\(f(x)=\tan x\), \(x \neq \dfrac{\pi}{2}+k \pi(k \in Z)\),它们统称三角函数.
解释
(1) 一般地,任意给定一个角\(α∈R\),它的终边\(OP\)与单位圆的交点是确定的,则点\(P\)的横坐标\(x\)、纵坐标\(y\)都是角\(α\)的函数;
(2) 当\(α=\dfrac{\pi}{2}+kπ(k∈Z)\)时,\(α\)的终边在\(y\)轴上,这时点\(P\)横坐标\(x=0\),此时 \(\dfrac{y}{x}=\tan \alpha\)没意义.
(3) 设\(α\)是一个任意角,它的终边上任意一点\(P\)(不与原点\(O\)重合)的坐标为\((x,y)\),点\(P\)与原点的距离为\(r\),
则\(\sin \alpha=\dfrac{y}{r}\),\(\cos \alpha=\dfrac{x}{r}\),\(\tan \alpha=\dfrac{y}{x}\).显然其中\(r=\sqrt{x^2+y^2}\).
【例】 求\(\sin \dfrac{2 \pi}{3}\), \(\cos \dfrac{2 \pi}{3}\), \(\tan \dfrac{2 \pi}{3}\).
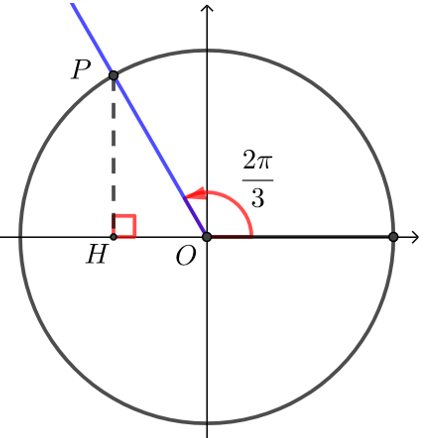
解析 下图中,\(\dfrac{2 \pi}{3}\)的终边\(OP\)与单位圆交于点\(P\),过点\(P\)作\(PH⊥x\)轴,
在\(Rt∆OPH\)中,\(OP=1\), \(\angle P O H=\dfrac{\pi}{3}\),
则\(O H=\dfrac{1}{2}\), \(P H=\dfrac{\sqrt{3}}{2}\),即\(P\left(-\dfrac{1}{2}, \dfrac{\sqrt{3}}{2}\right)\),
则\(\sin \dfrac{2 \pi}{3}=\dfrac{\sqrt{3}}{2}\),\(\cos \dfrac{2 \pi}{3}=-\dfrac{1}{2}\),\(\tan \dfrac{2 \pi}{3}=-\sqrt{3}\).
三角函数在各个象限的符号
判断三角函数在各个象限的符号的方法
(1) 三角函数定义
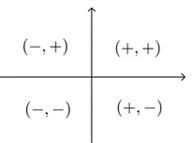
设\(α\)的终边上一点\(P(x,y)\),\(\sinα\)符号看\(y\),\(\cos α\)符号看\(x\),\(\tan α\)符号看 \(\dfrac{y}{x}\).
| 各象限点坐标的符号 | $α$ | 第一象限 | 第二象限 | 第三象限 | 第四象限 |
 | $\sinα$ | $+$ | $+$ | $-$ | $-$ |
| $\cos α$ | $+$ | $-$ | $-$ | $+$ | |
| $\tan α$ | $+$ | $-$ | $+$ | $-$ |
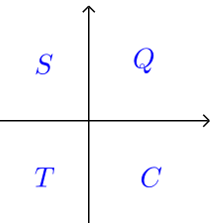
(2) 巧记方法: \(QSRC\)--全是天才
如下图,第一象限是\(Q\),第二象限是\(S\),第一象限是\(T\),第一象限是\(C\);\(QSRC\)是“全是天才”各字拼音首字母.\(S\)代表"\(\sin\)",\(T\)代表"\(\tan\) ",\(C\)代表"\(\cos\) ",\(Q\)代表全部三种函数.
则第一象限中三个函数符号都是正,第二象限中只有\(\sinα\)的符号是正,第三象限中只有\(\tan α\)的符号是正,第四象限只有\(\cos α\)的符号是正.
PS 建议学数学还是要有“逻辑性”地系统建立起知识体系,方法1好;方法2这种“取巧” 的分式不太建议,但挺佩服想到这方法那个人的想象能力.
特殊角的三角函数值表
| \(α\) | \(0\) | \(\dfrac{π}{6}\) | \(\dfrac{π}{4}\) | \(\dfrac{π}{3}\) | \(\dfrac{π}{2}\) | \(\dfrac{2π}{3}\) | \(\dfrac{3π}{4}\) | \(\dfrac{5π}{6}\) | \(π\) | \(\dfrac{3π}{2}\) | \(2π\) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| \(\sin α\) | \(0\) | \(\dfrac{1}{2}\) | \(\dfrac{\sqrt{2}}{2}\) | \(\dfrac{\sqrt{3}}{2}\) | \(1\) | \(\dfrac{\sqrt{3}}{2}\) | \(\dfrac{\sqrt{2}}{2}\) | \(\dfrac{1}{2}\) | \(0\) | \(-1\) | \(0\) |
| \(\cos α\) | \(1\) | \(\dfrac{\sqrt{3}}{2}\) | \(\dfrac{\sqrt{2}}{2}\) | \(\dfrac{1}{2}\) | \(0\) | \(-\dfrac{1}{2}\) | \(-\dfrac{\sqrt{2}}{2}\) | \(-\dfrac{\sqrt{3}}{2}\) | \(1\) | \(0\) | \(1\) |
| \(\tan α\) | \(0\) | \(\dfrac{\sqrt{3}}{3}\) | \(1\) | \(\sqrt{3}\) | 无 | \(-\sqrt{3}\) | \(-1\) | \(-\dfrac{\sqrt{3}}{3}\) | \(0\) | 无 | \(0\) |
利用三角函数的定义求\(α=0\)、 \(\dfrac{π}{2}\) 、\(π\)、\(2π\)时对应的三角函数值.
PS 对特殊角的三角函数值,要理解切忌死记,后面学到诱导公式也可理解.
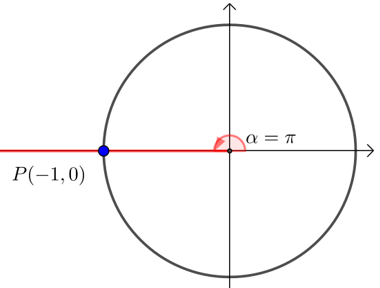
【例】 如图所示,\(α=π\)的终边在\(x\)轴的负半轴,与\(x\)轴交点为\(P(-1,0)\),
则\(\sinπ=0\),\(\cos π=-1\),\(\tan π=0\).
终边相等的角的三角函数值
由三角函数的定义,易得:终边相等的角的同一三角函数的值相等.
即\(\sin (α+k⋅2π)=\sinα\),\(\cos (α+k⋅2π)=\cos α\),\(\tan (α+k⋅2π)=\tan α\),其中\(k∈Z\).
这组公式属于诱导公式的公式一,后面我们还会学其他的公式二至六.
【例】 求 \(\cos \dfrac{9 \pi}{4}\), \(\tan \left(-\dfrac{11 \pi}{3}\right)\).
解 \(\cos \dfrac{9 \pi}{4}==\cos \left(\dfrac{\pi}{4}+2 \pi\right)=\cos \dfrac{\pi}{4}=\dfrac{\sqrt{2}}{2}\), \(\tan \left(-\dfrac{11 \pi}{3}\right)=\tan \left(-4 \pi+\dfrac{\pi}{3}\right)=\tan \dfrac{\pi}{3}=\dfrac{\sqrt{3}}{3}\).
基本方法
【题型1】利用定义求角的三角函数值
【典题1】 已知点\(M\)是单位圆\(x^2+y^2=1\)上的点,以射线\(OM\)为终边的角\(α\)的正弦值为\(-\dfrac{\sqrt{2}}{2}\),
求\(\cos α\)和\(\tan α\)的值.
解析 设点\(M\)的坐标为\((x_1,y_1)\).
由题意可知,\(\sin \alpha=-\dfrac{\sqrt{2}}{2}\),即\(y_1=-\dfrac{\sqrt{2}}{2}\).
\(∵\)点\(M\)是圆\(x^2+y^2=1\)上的点,
\(∴x_1^2+y_1^2=1\),即\(x_1^2+\left(-\dfrac{\sqrt{2}}{2}\right)^2=1\),解得\(x_1= \dfrac{\sqrt{2}}{2}\),或 \(x_1=-\dfrac{\sqrt{2}}{2}\).
即\(M\left(\dfrac{\sqrt{2}}{2},-\dfrac{\sqrt{2}}{2}\right)\)或\(M\left(-\dfrac{\sqrt{2}}{2},-\dfrac{\sqrt{2}}{2}\right)\),
\(\therefore \cos \alpha=\dfrac{\sqrt{2}}{2}\), \(\tan \alpha=-1\),或 \(\cos \alpha=-\dfrac{\sqrt{2}}{2}\), \(\tan \alpha=1\).
点拨 注意三角函数的定义,点\(M\)是否在单位圆上,若不是,则\(\sin \alpha=\dfrac{y}{\sqrt{x^2+y^2}}\),
\(\cos \alpha=\dfrac{x}{\sqrt{x^2+y^2}}\),\(\tan \alpha=\dfrac{y}{x}\).
【典题2】 求\(\sin \dfrac{3 \pi}{4}\),\(\cos \dfrac{3 \pi}{4}\),\(\tan \dfrac{3 \pi}{4}\).
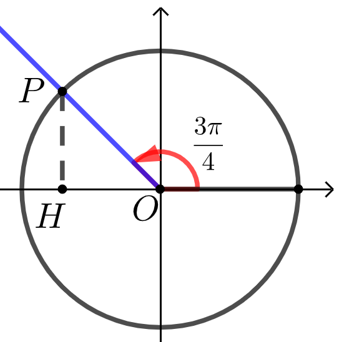
解析 \(\dfrac{3 \pi}{4}\)的终边\(OP\)与单位圆交于点\(P\),过点\(P\)作\(PH⊥x\)轴,
在\(Rt∆OPH\)中,\(OP=1\), \(\angle P O H=\dfrac{\pi}{4}\),
则\(O H=\dfrac{\sqrt{2}}{2}\), \(P H=\dfrac{\sqrt{2}}{2}\),即\(P\left(-\dfrac{\sqrt{2}}{2}, \dfrac{\sqrt{2}}{2}\right)\),
则\(\sin \dfrac{3 \pi}{4}=\dfrac{\sqrt{2}}{2}\),\(\cos \dfrac{3 \pi}{4}=-\dfrac{\sqrt{2}}{2}\),\(\tan \dfrac{3 \pi}{4}=-1\).
【巩固练习】
1.求 \(\sin \dfrac{\pi}{2}=\) \(\underline{\quad \quad}\), \(\cos \dfrac{\pi}{2}=\) \(\underline{\quad \quad}\) ,
2.已知角\(α\)的终边过点\(P(-4m,3m)(m≠0)\),则\(2\sinα+\cos α\)的值是( )
A.\(1\)或\(-1\) \(\qquad \qquad\) B. \(\dfrac{2}{5}\)或 \(-\dfrac{2}{5}\) \(\qquad \qquad\) C.\(1\)或 \(-\dfrac{2}{5}\) \(\qquad \qquad\) D.\(-1\)或 \(\dfrac{2}{5}\)
3.求\(\sin \left(-\dfrac{\pi}{4}\right)\),\(\cos \left(-\dfrac{\pi}{4}\right)\),\(\tan \left(-\dfrac{\pi}{4}\right)\).
参考答案
-
答案 \(1\),\(0\)
解析 利用单位圆,得到\(\sin \dfrac{\pi}{2}=1\),\(\cos \dfrac{\pi}{2}=0\). -
答案 \(B\)
解析 \(r=\sqrt{(-4 m)^2+(3 m)^2}=5|m|\), \(\therefore \sin \alpha=\dfrac{3 m}{5|m|}\), \(\cos \alpha=\dfrac{-4 m}{5|m|}\),
\(\therefore 2 \sin \alpha+\cos \alpha=\dfrac{6 m-4 m}{5|m|}=\dfrac{2 m}{5|m|}=-\dfrac{2}{5}\)或 \(\dfrac{2}{5}\),故选\(B\). -
答案 \(\sin \left(-\dfrac{\pi}{4}\right)=-\dfrac{\sqrt{2}}{2}\), \(\cos \left(-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\), \(\tan \left(-\dfrac{\pi}{4}\right)=-1\).
解析 \(-\dfrac{\pi}{4}\)的终边\(OP\)与单位圆交于点\(P\),过点\(P\)作\(PH⊥x\)轴,
在\(Rt∆OPH\)中,\(OP=1\), \(\angle P O H=\dfrac{\pi}{4}\),
则\(O H=\dfrac{\sqrt{2}}{2}\), \(P H=\dfrac{\sqrt{2}}{2}\),即\(P\left(\dfrac{\sqrt{2}}{2},-\dfrac{\sqrt{2}}{2}\right)\),
则\(\sin \left(-\dfrac{\pi}{4}\right)=-\dfrac{\sqrt{2}}{2}\),\(\cos \left(-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\),\(\tan \left(-\dfrac{\pi}{4}\right)=-1\).
【题型2】三角函数值的符号问题
【典题1】 判断下列各式的符号:
(1) \(\sinα⋅\tan α\),其中\(α\)是第四象限角;(2) \(\sin 3 \cdot \cos 4 \cdot \tan \left(-\dfrac{23 \pi}{4}\right)\).
解析 (1)\(∵α\)是第四象限角,\(∴\sinα<0\),\(\tan α<0\),
\(∴\sinα·\tan α>0\).
(2) \(\because \dfrac{\pi}{2}<3<\pi\), \(\pi<4<\dfrac{3 \pi}{2}\),\(∴\sin3>0\),\(\cos 4<0\).
\(\because-\dfrac{23 \pi}{4}=-6 \pi+\dfrac{\pi}{4}\), \(\therefore-\dfrac{23 \pi}{4}\)的终边与\(\dfrac{\pi}{4}\)的终边相同,
\(\because \tan \dfrac{\pi}{4}>0\), \(\therefore \tan \left(-\dfrac{23 \pi}{4}\right)>0\)
\(\therefore \sin 3 \cdot \cos 4 \cdot \tan \left(-\dfrac{23 \pi}{4}\right)<0\).
点拨 判断角\(α\)的三角函数的符号,先确定\(α\)终边在第几象限;设\(α\)的终边所在象限点坐标\((x,y)\),
\(\sinα\)符号看\(y\),\(\cos α\)符号看\(x\),\(\tan α\)符号看 \(\dfrac{y}{x}\).
【巩固练习】
1.已知\(\sin4\cdot \tan 2\)的值 ( )
A.不大于\(0\) \(\qquad \qquad \qquad\) B.大于\(0\) \(\qquad \qquad \qquad\) C.不小于\(0\) \(\qquad \qquad \qquad\) D.小于\(0\)
2.已知\(\{x∣x≠\dfrac{kπ}{2},k∈Z\}\),则函数\(y=\dfrac{|\sin x|}{\sin x}+\dfrac{|\cos x|}{\cos x}-\dfrac{2|\tan x|}{\tan x}\) 的值可能是( )
A.\(1\) \(\qquad \qquad \qquad \qquad\) B.\(-4\) \(\qquad \qquad \qquad \qquad\) C.\(4\) \(\qquad \qquad \qquad \qquad\) D.\(-2\)
3.若\(\cos θ<0\)且\(\tan θ<0\),则\(\dfrac{θ}{2}\)终边在( )
A.第一象限 \(\qquad \qquad\) B.第二象限 \(\qquad \qquad\) C.第一或第三象限 \(\qquad \qquad\) D.第三或第四象限
参考答案
-
答案 \(B\)
解析 \(4rad\)在第三象限,\(\sin4<0\);\(2rad\)在第二象限,\(\tan 2<0\),则\(\sin4\tan 2>0\).故选\(B\). -
答案 \(B\)
解析 当\(x\)在第一象限时: \(y=\dfrac{|\sin x|}{\sin x}+\dfrac{|\cos x|}{\cos x}-\dfrac{2|\tan x|}{\tan x}=1+1-2=0\);
当\(x\)在第二象限时: \(y=\dfrac{|\sin x|}{\sin x}+\dfrac{|\cos x|}{\cos x}-\dfrac{2|\tan x|}{\tan x}=1-1+2=2\) ;
当\(x\)在第三象限时: \(y=\dfrac{|\sin x|}{\sin x}+\dfrac{|\cos x|}{\cos x}-\dfrac{2|\tan x|}{\tan x}=-1-1-2=-4\);
当\(x\)在第四象限时: \(y=\dfrac{|\sin x|}{\sin x}+\dfrac{|\cos x|}{\cos x}-\dfrac{2|\tan x|}{\tan x}=-1+1+2=2\).
故选:\(B\). -
答案 \(C\)
解析 \(∵\cos θ<0\) ,\(∴θ\)是第二或三象限,
\(∵\tan θ<0\),\(∴θ\)是第二或四象限,
\(∴θ\)是第二象限,即 \(2 k \pi+\dfrac{\pi}{2}<\theta<2 k \pi+\pi\),
\(\therefore k \pi+\dfrac{\pi}{4}<\dfrac{\theta}{2}<k \pi+\dfrac{\pi}{2}\),
\(∴\)可得 \(\dfrac{θ}{2}\)终边在第一或第三象限.
故选:\(C\).
【题型3】诱导公式一的应用
【典题1】 求值 \(\cos \dfrac{7 \pi}{3}+\sin \dfrac{25 \pi}{6}+\tan \left(-\dfrac{15 \pi}{4}\right)\).
解析 \(\cos \dfrac{7 \pi}{3}+\sin \dfrac{25 \pi}{6}+\tan \left(-\dfrac{15 \pi}{4}\right)=\cos \left(2 \pi+\dfrac{\pi}{3}\right)+\sin \left(4 \pi+\dfrac{\pi}{6}\right)+\tan \left(-4 \pi+\dfrac{\pi}{4}\right)\)
\(=\cos \dfrac{\pi}{3}+\sin \dfrac{\pi}{6}+\tan \dfrac{\pi}{4}=\dfrac{1}{2}+\dfrac{1}{2}+1=2\).
点拨 \(\sin (α+k⋅2π)=\sinα\),\(\cos (α+k⋅2π)=\cos α\),\(\tan (α+k⋅2π)=\tan α\),
其中\(k∈Z\). 即终边相等的角的同一三角函数的值相等.
【典题2】 角\(α\)终边与单位圆交于点 \(A\left(-\dfrac{3}{5}, \dfrac{4}{5}\right)\),则 \(\sin (\alpha+4 \pi)+2 \tan (-2 \pi+\alpha)=\) \(\underline{\quad \quad}\) .
解析 \(∵\)角\(α\)终边与单位圆交于点 \(A\left(-\dfrac{3}{5}, \dfrac{4}{5}\right)\),
\(\therefore \sin \alpha=\dfrac{4}{5}\), \(\tan \alpha=-\dfrac{4}{3}\),
\(\therefore \sin (\alpha+4 \pi)+2 \tan (-2 \pi+\alpha)=\sin \alpha+2 \tan \alpha=\dfrac{4}{5}+2 \cdot\left(-\dfrac{4}{3}\right)=-\dfrac{28}{15}\).
【巩固练习】
1.求值 \(\cos \dfrac{13 \pi}{6}+\sin \dfrac{7 \pi}{3}+\tan \left(-\dfrac{7 \pi}{4}\right)\).
2.已知角\(α\)终边上点\(P\)的坐标为\(\left(\dfrac{4}{5},-\dfrac{3}{5}\right)\),则 \(3 \sin (\alpha-2 \pi)-2 \cos (6 \pi+\alpha)=\) \(\underline{\quad \quad}\) .
参考答案
-
答案 \(\sqrt{3}+1\)
解析 \(\cos \dfrac{13 \pi}{6}+\sin \dfrac{7 \pi}{3}+\tan \left(-\dfrac{7 \pi}{4}\right)=\cos \left(2 \pi+\dfrac{\pi}{6}\right)+\sin \left(2 \pi+\dfrac{\pi}{3}\right)+\tan \left(-2 \pi+\dfrac{\pi}{4}\right)\)\(=\cos \dfrac{\pi}{6}+\sin \dfrac{\pi}{3}+\tan \dfrac{\pi}{4}=\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{3}}{2}+1=\sqrt{3}+1\). -
答案 \(-\dfrac{17}{5}\)
解析 \(∵\)角\(α\)终边上点\(P\)的坐标为\(\left(\dfrac{4}{5},-\dfrac{3}{5}\right)\),
\(\therefore x=\dfrac{4}{5}\), \(y=-\dfrac{3}{5}\),\(r=|OA|=1\).
\(\therefore \sin \alpha=-\dfrac{3}{5}\),\(\cos \alpha=\dfrac{4}{5}\),
\(\therefore 3 \sin (\alpha-2 \pi)-2 \cos (6 \pi+\alpha)=3 \sin \alpha-2 \cos \alpha=-\dfrac{9}{5}-\dfrac{8}{5}=-\dfrac{17}{5}\).
分层练习
【A组---基础题】
1.有下列命题,其中正确的个数是( )
①终边相同的角的同名三角函数值相等;
②同名三角函数值相等的角也相等;
③终边不相同,它们的同名三角函数值一定不相等;
④不相等的角,同名三角函数值也不相等.
A.\(0\) \(\qquad \qquad \qquad \qquad\) B.\(1\) \(\qquad \qquad \qquad \qquad\) C.\(2\) \(\qquad \qquad \qquad \qquad\) D.\(3\)
2.已知角\(α\)的项点与坐标原点重合,始边与\(x\)轴的非负半轴重合,若点\(P(2,-1)\)在角\(α\)的终边上,则\(\tan α=\)( )
A.\(2\) \(\qquad \qquad \qquad \qquad\) B. \(\dfrac{1}{2}\) \(\qquad \qquad \qquad \qquad\) C. \(-\dfrac{1}{2}\) \(\qquad \qquad \qquad \qquad\) D.\(-2\)
3.已知\(\sin \alpha=\dfrac{3}{5}\), \(\cos \alpha=-\dfrac{4}{5}\),则角\(α\)所在的象限是( )
A.第一象限 \(\qquad \qquad \qquad\) B.第二象限 \(\qquad \qquad \qquad\) C.第三象限 \(\qquad \qquad \qquad\) D.第四象限
4.已知\(\alpha=\dfrac{16 \pi}{5}\),则下列结论正确的是( )
A. \(\sin α<0\),\(\cos α>0\) $ \qquad \qquad \qquad \qquad$ B. \(\sin α<0\),\(\cos α<0\)
C.\(\sin α<0\),\(\cos α<0\) \(\qquad \qquad \qquad \qquad\) D.\(\sin α>0\),\(\cos α>0\)
5.若\(\sinα·\cos α<0\),则\(α\)的终边在( )
A.第一或第二象限 \(\qquad \qquad\) B.第一或第三象限 \(\qquad \qquad\) C.第一或第四象限 \(\qquad \qquad\) D.第二或第四象限
6.\(\sin495°=\)( )
A.\(1\) \(\qquad \qquad \qquad \qquad\) B. \(-\dfrac{1}{2}\) \(\qquad \qquad \qquad \qquad\) C. \(\dfrac{\sqrt{3}}{2}\) \(\qquad \qquad \qquad \qquad\) D. \(\dfrac{\sqrt{2}}{2}\)
7.已知角\(α\)的终边与单位圆的交点为\(P\left(-\dfrac{4}{5}, \dfrac{3}{5}\right)\),则\(2\cos α+\tan α=\)\(\underline{\quad \quad}\).
8.已知\(P\left(\sin \dfrac{5 \pi}{4}, \cos \dfrac{3 \pi}{4}\right)\)落在角\(θ\)的终边上,且\(θ∈[0,2π)\),则\(θ\)是第\(\underline{\quad \quad}\)象限角.
9.已知函数\(f(x)=a \sin (\pi x+\alpha)+b \cos (\pi x+\beta)\),且\(f(2)=2\),则\(f(2020)\)的值为\(\underline{\quad \quad}\).
10.求值\(\sin \left(-\dfrac{11 \pi}{6}\right)+\cos \dfrac{7 \pi}{3}+\tan \left(-\dfrac{5 \pi}{3}\right)\).
11.已知角\(α\)终边上点\(P\)的坐标为\((2,-1)\),求\(3 \tan (\alpha+2 \pi)+\sin (-4 \pi+\alpha)\).
参考答案
-
答案 \(B\)
解析 对于①,由诱导公式一可得正确;
对于②,由 \(\sin 30^{\circ}=\sin 150^{\circ}=\dfrac{1}{2}\),但\(30°≠150°\),所以②错误;
对于③,如\(α=60°\),\(β=120°\)的终边不相同,但 \(\sin 60^{\circ}=\sin 120^{\circ}=\dfrac{\sqrt{3}}{2}\),
所以③错误;对于④,由③中的例子可知④错误. -
答案 \(C\)
解析 \(∵\)点\(P(2,-1)\)在角\(α\)的终边上, \(\therefore \tan \alpha=\dfrac{-1}{2}=-\dfrac{1}{2}\),故选:\(C\). -
答案 \(B\)
解析 由 \(\sin \alpha=\dfrac{3}{5} >0\)得角\(α\)的终边在第一或第二象限;
由 \(\cos \alpha=-\dfrac{4}{5}<0\)得角\(α\)的终边在第二或第三象限.
综上,角\(α\)所在的象限是第二象限. -
答案 \(C\)
解析 \(\because \alpha=\dfrac{16 \pi}{5}=2 \pi+\pi+\dfrac{\pi}{5}\),终边落在第三象限,
\(∴\sin α<0\),\(\cos α<0\),故选:\(C\). -
答案 \(D\)
解析 \(∵\sinα·\cos α<0\),\(∴\sinα\)与\(\cos α\)异号,
\(∴α\)的终边在第二或第四象限. -
答案 \(D\)
解析 \(\sin 495^∘=\sin (360^∘+135^∘ )=\sin 135^∘=\dfrac{\sqrt{2}}{2}\),故选\(D\). -
答案 \(\dfrac{9}{20}\)
解析 角\(α\)的终边与单位圆的交点为\(P\left(-\dfrac{4}{5}, \dfrac{3}{5}\right)\),则 \(\cos \alpha=-\dfrac{4}{5}\),
则 \(2 \sin \alpha+\tan \alpha=\dfrac{6}{5}+\dfrac{\frac{3}{5}}{-\frac{4}{5}}=\dfrac{9}{20}\). -
答案 三
解析 \(\because \sin \dfrac{5 \pi}{4}<0\), \(\cos \dfrac{3 \pi}{4}<0\),\(∴P\)在第三象限,\(∴θ\)在第三象限角. -
答案 \(2\)
解析 \(∵f(2)=a \sin (2π+α)+b \cos (2π+β)=a\sin α+b\cos β\),\(∴a \sin α+b \cos β=2\)
\(f(2020)=a \sin (2020x+α)+b \cos (2020x+β)=a \sin α+b \cos β=2\). -
答案 \(\sqrt{3}+1\)
解析 \(\sin \left(-\dfrac{11 \pi}{6}\right)+\cos \dfrac{7 \pi}{3}+\tan \left(-\dfrac{7 \pi}{3}\right)=\sin \left(-2 \pi+\dfrac{\pi}{6}\right)+\cos \left(2 \pi+\dfrac{\pi}{3}\right)+\tan \left(-2 \pi+\dfrac{\pi}{3}\right)\)
\(=\sin \dfrac{\pi}{6}+\cos \dfrac{\pi}{3}+\tan \dfrac{\pi}{3}=\dfrac{1}{2}+\dfrac{1}{2}+\sqrt{3}=\sqrt{3}+1\). -
答案 \(-\dfrac{3}{2}-\dfrac{\sqrt{5}}{5}\)
解析 \(∵\)角\(α\)终边上点\(P\)的坐标为\((2,-1)\),
\(∴x=2\),\(y=-1\), \(r=|O A|=\sqrt{5}\),
\(\therefore \sin \alpha=\dfrac{y}{r}=-\dfrac{\sqrt{5}}{5}\), \(\tan \alpha=\dfrac{y}{x}=-\dfrac{1}{2}\),
\(\therefore 3 \tan (\alpha+2 \pi)+\sin (-4 \pi+\alpha)=3 \tan \alpha+\sin \alpha=-\dfrac{3}{2}-\dfrac{\sqrt{5}}{5}\).
【B组---提高题】
1.若\(θ\)为第二象限角,则下列结论一定成立的是( )
A. \(\sin \dfrac{\theta}{2}>0\) \(\qquad \qquad \qquad\) B.\(\cos \dfrac{\theta}{2}>0\) \(\qquad \qquad \qquad\) C.\(\tan \dfrac{\theta}{2}>0\) \(\qquad \qquad \qquad\) D.\(\sin \dfrac{\theta}{2} \cos \dfrac{\theta}{2}<0\)
2.若\(\sin \left(-\dfrac{7 \pi}{3}+\theta\right)=-\dfrac{3}{5}\),则\(\sin \left(\theta-\dfrac{\pi}{3}\right)=\) \(\underline{\quad \quad}\) .
参考答案
-
答案 \(C\)
解析 \(∵θ\)为第二象限角, \(\therefore \dfrac{\pi}{2}+2 k \pi<\theta<\pi+2 k \pi\),\(k∈Z\).
则 \(\dfrac{\pi}{4}+k \pi<\dfrac{\theta}{2}<\dfrac{\pi}{2}+k \pi\),\(k∈Z\),
\(∴θ\)为一或三象限角,得 \(\tan \dfrac{\theta}{2}>0\).
故选:\(C\). -
答案 \(-\dfrac{3}{5}\)
解析 \(\sin \left(\theta-\dfrac{\pi}{3}\right)=\sin \left[2 \pi+\left(-\dfrac{7 \pi}{3}+\theta\right)\right]=\sin \left(-\dfrac{7 \pi}{3}+\theta\right)=-\dfrac{3}{5}\).
【C组---拓展题】
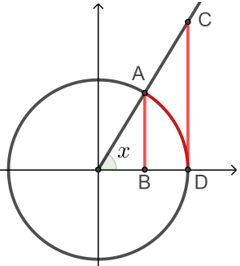
1.若 \(0<x<\dfrac{\pi}{2}\),证明 \(\sin x<x<\tan x\).
参考答案
- 解析 如上图,在单位圆中,\(\sin x=AB\),\(\tan x=CD\), \(x=\widehat{A D}\),
显然\(\sin x<x<\tan x\).


 浙公网安备 33010602011771号
浙公网安备 33010602011771号