5.1.2 弧度制
${\color{Red}{欢迎到学科网下载资料学习 }}$
【基础过关系列】2022-2023学年高一数学上学期同步知识点剖析精品讲义(人教A版2019)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第一册同步巩固,难度2颗星!
基础知识
弧度的定义
弧长等于半径时,所对的圆心角为\(1\)弧度的圆心角,记作\(1\mathrm{rad}\).
即:半径为\(r\)的圆中,弧长为\(l\)的弧所对的圆心角为\(\alpha \mathrm{rad}\),那么\(|\alpha|=\dfrac{l}{r}\).
解释
(1) 如下图,设\(α=n^{\circ}\),\(OP=r\),圆弧\(\widehat{P P}_1\) ̂的长为\(l\),\(OQ=r_1\),圆弧\(\widehat{Q Q}_1\)的长为\(l_1\).
由初中所学的弧长公式\(l=\dfrac{n \pi r}{180}\),可得\(\dfrac{l}{r}=n \dfrac{\pi}{180}\).
同理\(\dfrac{l_1}{r_1}=n \dfrac{\pi}{180}\),则\(\dfrac{l_1}{r_1}=\dfrac{l}{r}\),即圆心角\(α\)所对的弧长与半径的比值,只与\(α\)的大小有关.
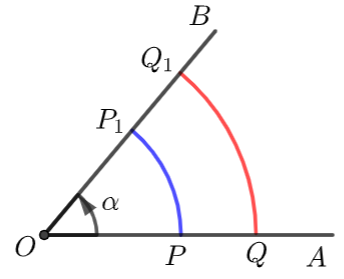
(2) \(|\alpha|=\dfrac{l}{r}\),其中\(α\)的正负由角\(α\)的终边旋转方向决定,即逆时针旋转为正,顺时针旋转为负.
角度与弧度的转化
(1) \(180^{\circ}=\pi \mathrm{rad} \Rightarrow 1^{\circ}=\dfrac{\pi}{180} \approx 0.01745 \mathrm{rad}\), \(1 \mathrm{rad}=\left(\dfrac{180}{\pi}\right)^{\circ} \approx 57.30^{\circ}\).
(2) 特殊角的角度与弧度对应表
| 角度 | \(0^∘\) | \(30^∘\) | \(45^∘\) | \(60^∘\) | \(90^∘\) | \(120^∘\) | \(135^∘\) | \(150^∘\) | \(180^∘\) | \(270^∘\) | \(360^∘\) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 弧度 | \(0\) | \(\dfrac{\pi}{6}\) | \(\dfrac{\pi}{4}\) | \(\dfrac{\pi}{3}\) | \(\dfrac{\pi}{2}\) | \(\dfrac{2\pi}{3}\) | \(\dfrac{3\pi}{4}\) | \(\dfrac{5\pi}{6}\) | \(\pi\) | \(\dfrac{3\pi}{2}\) | \(2\pi\) |
注 在弧度制下,角的集合与实数集之间建立一一对应关系;以后弧度制单位\(\mathrm{rad}\)可省略不写.
【例】 \(\dfrac{2\pi}{5}\)化成角度为\(\underline{\quad \quad}\).
解 \(\dfrac{2 \pi}{5}=\dfrac{2}{5} \cdot 180^{\circ}=72^{\circ}\).
弧长与扇形面积计算公式
弧长\(l=α\cdot R\); 扇形面积\(S=\dfrac{1}{2} l R=\dfrac{1}{2} \alpha R^2\), 其中\(R\)是圆的半径,\(α(0<α<2π)\)为圆心角.
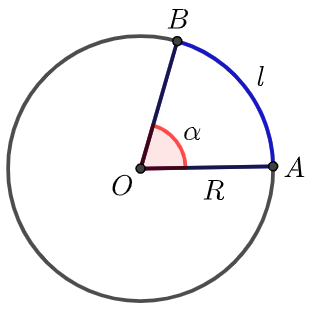
证明
由公式\(|\alpha|=\dfrac{l}{r}\)可得\(l=αR\),
由于初中所学可知\(l=\dfrac{n \pi R}{180}\),\(S=\dfrac{n \pi R^2}{360}\),
所以\(S=\dfrac{n \pi R^2}{360}=\dfrac{1}{2} \cdot \dfrac{n \pi R}{180} \cdot R=\dfrac{1}{2} l R=\dfrac{1}{2} \cdot \alpha R \cdot R=\dfrac{1}{2} \alpha R^2\).
【例】 一扇形中,圆心角为\(\dfrac{π}{3}\),半径\(r=2\),求圆心角所对的弧长和扇形面积.
解 \(l=2\cdot \dfrac{π}{3}=\dfrac{2π}{3}\),\(S=\dfrac{1}{2} αR^2=\dfrac{1}{2} \cdot \dfrac{π}{3}\cdot 4=\dfrac{2π}{3}\).
基本方法
【题型1】弧度制的概念
【典题1】 圆弧长度等于其圆内接正三角形的边长,则其圆心角的弧度数为( )
A. \(\dfrac{\pi}{3}\) \(\qquad \qquad\) B. \(\dfrac{2\pi}{3}\) \(\qquad \qquad\) C.\(\sqrt{3}\) \(\qquad \qquad\) D.\(2\)
解析 设圆的半径为\(R\),则圆的内接正三角形的边长为\(\sqrt{3}R\),
所以圆心角的弧度数为\(\dfrac{\sqrt{3} R}{R}=\sqrt{3}\).
点拨 考核弧度的定义:半径为r的圆中,弧长为l的弧所对的圆心角为\(α rad\),那么 \(|\alpha|=\dfrac{l}{r}\).
【巩固练习】
1.在圆心角均为\(1\)弧度的若干个圆中,下列结论正确的是( )
A.所对的弧长相等 \(\qquad \qquad \qquad \qquad\) B.所对的弦长相等
C.所对的弧长等于各自圆的半径 \(\qquad \qquad\) D.所对的弦长等于各自圆的半径
2.下面各命题中,是假命题的为( ).
A.“度”与“弧度”是度量 角的两种不同的度量单位;
B.\(1\)度的角是周角的\(\dfrac{1}{360}\),\(1\)弧度的角是周角的\(\dfrac{1}{2 \pi}\);
C.根据弧度的定义,\(180°\)一定等于\(π\)弧度;
D.不论是用角度制 还是用弧度制度量角,它们均与所在圆的半径长短有关.
3.圆弧长度等于其圆内接正四边形的边长,则其圆心角的弧度数为( )
A.\(\dfrac{\pi}{4}\) \(\qquad \qquad \qquad \qquad\) B.\(\dfrac{\pi}{2}\) \(\qquad \qquad \qquad \qquad\) C. \(\sqrt{2}\) \(\qquad \qquad \qquad \qquad\) D.\(2\)
参考答案
-
答案 \(C\)
解析 \(∵l=θR\),\(θ=1\),\(∴l=R\),故选\(C\). -
答案 \(D\)
解析 根据角度和弧度的定义,可知无论是角度制还是弧度制,角的大小与所在圆的半径长短无关,
而是与弧长和半径的比值有关,所以\(D\)是假命题. -
答案 \(C\)
【题型2】弧度制与角度制的换算
【典题1】 设\(α_1=510^{\circ}\),\(α_2=-750^{\circ}\), \(\beta_1=\dfrac{4}{5} \pi\), \(\beta_2=-\dfrac{11}{6} \pi\).
(1)将\(α_1\),\(α_2\)用弧度表示出来,并指出它们各自终边所在的象限;
(2)将\(β_1\),\(β_2\)用角度表示出来,并在\([-2π,2π)\)内找出与它们终边相同的所有的角.
解析 (1) \(\because 1^{\circ}=\dfrac{\pi}{180} \mathrm{rad}\),
\(\therefore \alpha_1=510^{\circ}=510 \times \dfrac{\pi}{180}=\dfrac{17}{6} \pi=2 \pi+\dfrac{5}{6} \pi\);
\(\alpha_2=-750^{\circ}=-750 \times \dfrac{\pi}{180}=-\dfrac{25}{6} \pi=-3 \times 2 \pi+\dfrac{11}{6} \pi\).
\(∴α_1\)的终边在第二象限,\(α_2\)的终边在第四象限.
(2) \(\beta_1=\dfrac{4}{5} \pi=\dfrac{4 \pi}{5} \times\left(\dfrac{180}{\pi}\right)^{\circ}=144^{\circ}\).
设\(θ_1=k·360^{\circ}+144^{\circ}(k∈Z)\).
\(∵-360^{\circ}≤θ_1<360^{\circ}\),
\(∴-360^{\circ}≤k·360^{\circ}+144^{\circ}<360^{\circ}\).
\(∴k=-1\)或\(k=0\).
\(∴\)在\([-2π,2π)\)内与\(β_1\)终边相同的角是\(-216^{\circ}\)角.
\(\beta_2=-\dfrac{11}{6} \pi=-\dfrac{11 \pi}{6} \times\left(\dfrac{180}{\pi}\right)=-330^{\circ}\).
设\(θ_2=k·360^{\circ}-330^{\circ}(k∈Z)\).
\(∵-360^{\circ}≤θ_2<360^{\circ}\),
\(∴-360^{\circ}≤k·360^{\circ}-330^{\circ}<360^{\circ}\).
\(∴k=0\)或\(k=1\).
\(∴\)在\([-2π,2π)\)内与\(β_2\)终边相同的角是\(30^{\circ}\)角.
【巩固练习】
1.下列各式中正确的是 ( )
A.\(\dfrac{\pi}{6} \mathrm{rad}=60^{\circ}\) \(\qquad \qquad\) B.\(\dfrac{3 \pi}{4} \mathrm{rad}=120^{\circ}\) \(\qquad \qquad\) C.\(150^{\circ}=\dfrac{5 \pi}{6} \mathrm{rad}\) \(\qquad \qquad\) D.\(180^∘=2π \mathrm{rad}\)
2.\(3\)弧度的角终边在( )
A.第一象限 \(\qquad \qquad \qquad\) B.第二象限 \(\qquad \qquad \qquad\) C.第三象限 \(\qquad \qquad \qquad\) D.第四象限
3.已知角\(α=1200^{\circ}\)
(1)将\(α\)改写成\(β+2kπ(k∈Z,0≤β≤2π)\)的形式,并指出\(α\)是第几象限的角;
(2)在区间\([-4π,π]\)上找出与\(α\)终边相同的角.
参考答案
-
答案 \(C\)
解析 \(\therefore \pi \mathrm{rad}=180^{\circ}\), \(\therefore \dfrac{\pi}{6} \mathrm{rad}=\dfrac{1}{6} \times 180^{\circ}=30^{\circ}\), \(\dfrac{3 \pi}{4} \mathrm{rad}=\dfrac{3}{4} \times 180^{\circ}=135^{\circ}\),
\(\dfrac{5 \pi}{6} \mathrm{rad}=\dfrac{5}{6} \times 180^{\circ}=150^{\circ}\),故选:\(C\). -
答案 \(B\)
解析 因为\(\dfrac{\pi}{2}<3<\pi\),所以\(3\)弧度的角终边在第二象限.故选:\(B\). -
答案 (1) \(\alpha=3 \times 2 \pi+\dfrac{2 \pi}{3}\), 第二象限角; (2) \(-\dfrac{10 \pi}{3},-\dfrac{4 \pi}{3}\).
解析 (1) \(\because \alpha=1200^{\circ}=1200 \times \dfrac{\pi}{180} \mathrm{rad}=\dfrac{20 \pi}{3}=3 \times 2 \pi+\dfrac{2 \pi}{3} \mathrm{rad}\),
又 \(\because \dfrac{\pi}{2}<\dfrac{2 \pi}{3}<\pi\),
\(∴\)角\(α\)与\(\dfrac{2 \pi}{3}\)的终边相同,角\(α\)是第二象限角.
(2)\(∵\)与角\(α\)终边相同的角(含角\(α\)在内)为 \(2 k \pi+\dfrac{2 \pi}{3}\),\(k∈Z\),
\(∴\)由 \(-4 \pi \leq 2 k \pi+\dfrac{2 \pi}{3} \leq \pi\),得 \(-\dfrac{14 \pi}{3} \leq 2 k \pi \leq-\dfrac{\pi}{3}\),
\(k=-2\),\(k=-1\)时,不等式成立.
\(∴\)在区间\([-4π,π]\)上与角\(α\)终边相同的角是\(-\dfrac{10 \pi}{3},-\dfrac{4 \pi}{3}\).
【题型3】扇形的弧长与面积公式的应用
【典题1】 半径为\(12cm\)的轮子,每\(3\)分钟转\(1000\)圈,试求:
(1)它的平均角速度(\(1\)秒钟转过的弧度数);
(2)轮沿上一点\(1\)秒经过的距离;
(3)轮沿上一点转过\(1000°\)所经过的距离.
解析 (1)每\(3\)分钟转\(1000\)圈,则它的平均角速度为 \(\omega=\dfrac{1000 \times 2 \pi}{3 \times 60}=\dfrac{100 \pi}{9}\) (弧度/秒);
(2)轮沿上一点\(1\)秒经过的距离为 \(s=v t=\omega r t=\dfrac{100 \pi}{9} \times 12 \times 1=\dfrac{400 \pi}{3}(\mathrm{~cm})\);
(3)轮沿上一点转过\(1000°\)所经过的距离为 \(1000 \times \dfrac{2 \pi}{360} \times 12=\dfrac{200 \pi}{3}(\mathrm{~cm})\).
【典题2】已知扇形\(AOB\)的圆心角为\(α\),周长为\(14\).
(1)若这个扇形面积为\(10\),且\(α\)为锐角,求\(α\)的大小;
(2)求这个扇形的面积取得最大值时圆心角\(α\)的大小和弦长\(AB\).
解析 设扇形\(AOB\)的半径为\(r\),弧长为\(l\),圆心角为\(α\),
(1)由题意知 \(\left\{\begin{array}{l}
2 r+l=14 \\
\dfrac{1}{2} l r=10
\end{array}\right.\),解得: \(\left\{\begin{array}{l}
r=5 \\
l=4
\end{array}\right.\),或 \(\left\{\begin{array}{l}
r=2 \\
l=10
\end{array}\right.\),
\(\therefore \alpha=\dfrac{l}{r}=\dfrac{4}{5}\)或\(5\);
\(∵α\)为锐角, \(\therefore \alpha=\dfrac{4}{5}\).
(2)\(∵2r+l=14\),
\(\therefore S=\dfrac{1}{2} l r=\dfrac{1}{4} \cdot l \cdot 2 r \leq \dfrac{1}{4}\left(\dfrac{l+2 r}{2}\right)^2=\dfrac{1}{4} \times 7^2=\dfrac{49}{4}\),
当且仅当\(2r=l\),即 \(\alpha=\dfrac{l}{r}=2\)时,面积取得最大值 \(\dfrac{49}{4}\),
\(\therefore r=\dfrac{7}{2}\), \(\therefore\)弦长 \(A B=\dfrac{7}{2} \sin 1 \times 2=7 \sin 1\).
【巩固练习】
1.已知圆锥的侧面展开图是一个半径为\(2cm\),圆心角为\(\dfrac{2 \pi}{3}\)的扇形,则此圆锥的高为\(\underline{\quad \quad}\)\(cm\).
2.若扇形\(OAB\)的面积是\(1 cm^2\),它的周长是\(4 cm\),求扇形圆心角的弧度数.
3.已知\(2rad\)的圆心角所对的弦长为\(2\),求这个圆心角所对的弧长.
4.已知扇形\(AOB\)的周长为\(8\).
(1)若这个扇形的面积为\(3\),求圆心角的大小;
(2)求这个扇形的面积取得最大值时圆心角的大小和弦长\(AB\).

参考答案
-
答案 \(\dfrac{4 \sqrt{2}}{3}\)
解析 设此圆的底面半径为\(r\),高为\(h\),母线为\(l\),
∵圆锥的侧面展开图是一个半径为\(2cm\),圆心角为\(\dfrac{2 \pi}{3}\)的扇形,
\(∴l=2\),得 \(2 \pi r=\dfrac{2 \pi}{3} \times l=\dfrac{4 \pi}{3}\),解之得 \(r=\dfrac{2}{3}\),
因此,此圆锥的高 \(h=\sqrt{l^2-r^2}=\sqrt{2^2-\left(\dfrac{2}{3}\right)^2}=\dfrac{4 \sqrt{2}}{3} \mathrm{~cm}\).
故答案为: \(\dfrac{4 \sqrt{2}}{3}\).

-
答案 \(2\)
解析 设扇形的半径为\(R\),弧长为\(l\),
由已知得\(\left\{\begin{array}{l} \dfrac{1}{2} l R=1 \\ 2 R+l=4 \end{array}\right.\)解得\(\left\{\begin{array}{l} l=2 \\ R=1 \end{array}\right.\),
\(∴\)扇形圆心角的弧度数是\(\dfrac{l}{R}=2\). -
答案 \(\dfrac{2}{\sin 1}\)
解析 如图,

\(∠AOB=2\),过\(O\)点作\(OC⊥AB\)于\(C\),并延长\(OC\)交于\(D\).\(∠AOD=∠BOD=1\),
且\(AC= AB=1.\)在\(Rt△AOC\)中, \(A O=\dfrac{A C}{\sin \angle A O C}=\dfrac{1}{\sin 1}\),
从而弧\(AB\)的长为 \(l=|\alpha| \cdot r=\dfrac{2}{\sin 1}\). -
答案 (1) \(θ=6\)或 \(\dfrac{2}{3}\); (2) \(θ=2\),\(AB=4\sin1\).
解析 设扇形的半径为\(r\),中心角为\(θ\),则\(2r+θr=8\),\(θ∈[0,2π]\).
(1)由题意可得:\(S=\dfrac{1}{2} \theta r^2=3\),
又\(2r+θr=8\),
联立解得 \(θ=6\)或 \(\dfrac{2}{3}\).
(2) \(S=\dfrac{1}{2} \theta r^2=\dfrac{1}{2} \times \dfrac{8-2 r}{r} \times r^2=(4-r) r \leq\left(\dfrac{4-r+r}{2}\right)^2=4\),
当且仅当\(r=2\),\(θ=2\).
\(∴AB=2×2\sin1=4\sin1\).
分层练习
【A组---基础题】
- \(\dfrac{7}{12} \pi=\)( )
A.\(70^{\circ}\) \(\qquad \qquad\qquad \qquad\) B.\(75^{\circ}\) \(\qquad \qquad\qquad \qquad\) C.\(80^{\circ}\) \(\qquad \qquad\qquad \qquad\) D.\(105^{\circ}\)
2.若\(α=5 rad\),则角\(α\)的终边所在的象限为( )
A.第一象限 \(\qquad \qquad \qquad\) B.第二象限 \(\qquad \qquad \qquad\) C.第三象限 \(\qquad \qquad \qquad\) D.第四象限
3.终边在\(y\)轴的非负半轴上的角的集合是( )
A.\(\{α|α=kπ,k∈Z\}\) \(\qquad \qquad \qquad \qquad\) B.\(\left\{\alpha \mid \alpha=k \pi+\dfrac{\pi}{2}, k \in Z\right\}\)
C.\(\{α|α=2kπ,k∈Z\}\) \(\qquad \qquad \qquad \qquad\) D. \(\left\{\alpha \mid \alpha=2k \pi+\dfrac{\pi}{2}, k \in Z\right\}\)
4.若弧度为\(2 \alpha\left(0<\alpha<\dfrac{\pi}{2}\right)\)的圆心角所对弦长为\(m\),则该圆心角所对的弧长为( )
A. \(\dfrac{a m}{\sin \alpha}\) \(\qquad \qquad \qquad\) B. \(\dfrac{a m}{\cos \alpha}\) \(\qquad \qquad \qquad\) C.\(\dfrac{a m}{2\sin \alpha}\) \(\qquad \qquad \qquad\) D. \(\dfrac{a m}{2\cos \alpha}\)
5.已知圆\(O\)与直线\(l\)相切于点\(A\),点\(P,Q\)同时从\(A\)点出发,\(P\)沿着直线\(l\)向右、\(Q\)沿着圆周按逆时针以相同的速度运动,当\(Q\)运动到点\(A\)时,点\(P\)也停止运动,连接\(OQ\),\(OP\)(如图),则阴影部分面积\(S_1\),\(S_2\)的大小关系是( )

A.\(S_1=S_2\)
B.\(S_1≤S_2\)
C.\(S_1≥S_2\)
D.先\(S_1<S_2\),再\(S_1=S_2\),最后\(S_1>S_2\)
6.在直径为\(20cm\)的圆中,圆心角为\(150^{\circ}\)时所对的弧长为\(\underline{\quad \quad}\).
7.若\(α\)角与\(-\dfrac{8 \pi}{5}\)角终边相同,则在\([0,2π]\)内终边与\(-\dfrac{\alpha}{4}\)角终边相同的角是\(\underline{\quad \quad}\) .
8.(1)把\(-1480^{\circ}\)写成\(α+2kπ(k∈Z)\)的形式,其中\(0≤α<2π\);
(2)若\(β∈[-4π,0]\),且\(β\)与(1)中\(α\)的终边相同,求\(β\).
9.已知相互啮合的两个齿轮,大轮有\(60\)齿,小轮有\(45\)齿.
(1)当小轮转动一周时,求大轮转动的弧度数;
(2)当小轮的转速是 \(120 \mathrm{r} / \mathrm{min}\)时,大轮上每\(1s\)转过的弧长是\(60πcm\),求大轮的半径.
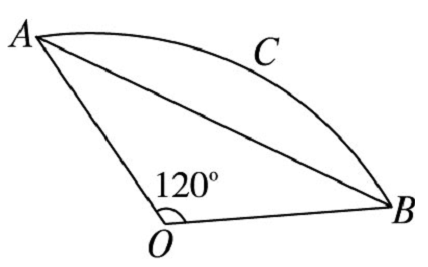
10.如下图所示,已知扇形\(AOB\)的圆心角为\(120^{\circ}\),半径长为\(6\),求弓形\(ACB\)的面积.
参考答案
-
答案 \(D\)
解析 \(\dfrac{7}{12} \pi=\dfrac{7}{12} \times 180^{\circ}=105^{\circ}\).故选:\(D\). -
答案 \(D\)
-
答案 \(D\)
解析 \(A\)选项表示的角的终边在\(x\)轴上;\(B\)选项表示的角的终边在\(y\)轴上;
\(C\)选项表示的角的终边在\(x\)轴非负半轴上;\(D\)选项表示的角的终边在\(y\)轴非负半轴上,
故选\(D\). -
答案 \(A\)
解析 设圆的半径为\(r\),由弧度为\(2 \alpha\left(0<\alpha<\dfrac{\pi}{2}\right)\)的圆心角所对弦长为\(m\),
则\(\sin \alpha=\dfrac{\dfrac{m}{2}}{r}=\dfrac{m}{2 r}\),\(r=\dfrac{m}{2 \sin \alpha}\);
该圆心角所对的弧长为\(l=2 \alpha r=\dfrac{m \alpha}{\sin \alpha}\).
故选:\(A\). -
答案 \(A\)
解析 如图所示,

\(∵\)直线\(l\)与圆\(O\)相切,\(∴OA⊥AP\),
\(\therefore S_{\text {扇形 } A O Q}=\dfrac{1}{2} \cdot \widehat{A Q} \cdot r=\dfrac{1}{2} \cdot \widehat{A Q} \cdot O A\), \(S_{\triangle A O P}=\dfrac{1}{2} \cdot O A \cdot A P\),
\(\because \widehat{A Q}=A P\),
\(\therefore S_{\text {扇形 } \mathrm{AOQ}}=S_{\triangle A O P}\),即 \(S_{\text {扇形 } \mathrm{AOQ}}-S_{\text {扇形 } \mathrm{AOB}}=S_{\triangle A O P}-S_{\text {扇形 AOB }}\),
\(∴S_1=S_2\).
故选:\(A\). -
答案 \(\dfrac{25 \pi}{3} \mathrm{~cm}\)
解析 \(150^{\circ}=150 \times \dfrac{\pi}{180}=\dfrac{5 \pi}{6}, \quad \therefore l=\dfrac{5 \pi}{6} \times 10=\dfrac{25 \pi}{3} \mathrm{~cm}\). -
答案 \(\dfrac{2 \pi}{5}, \dfrac{9 \pi}{10}, \dfrac{7 \pi}{5}, \dfrac{19 \pi}{10}\)
解析 依题意, \(\alpha=2 k \pi+\dfrac{8 \pi}{5}, k \in z\), \(\therefore \dfrac{\alpha}{4}=\dfrac{k \pi}{2}+\dfrac{2 \pi}{5}, k \in z\),
又 \(\dfrac{\alpha}{4} \in[0,2 \pi]\), \(\therefore k=0, \alpha=\dfrac{2 \pi}{5}\); \(k=1, \alpha=\dfrac{9 \pi}{10}\); \(k=2, \alpha=\dfrac{7 \pi}{5}\); \(k=3, \alpha=\dfrac{19 \pi}{10}\);
故 答案为 \(\dfrac{2 \pi}{5}, \dfrac{9 \pi}{10}, \dfrac{7 \pi}{5}, \dfrac{19 \pi}{10}\). -
答案 (1) \(-1480^{\circ}=\dfrac{16}{9} \pi-2 \times 5 \pi\) (2)\(-\dfrac{2 \pi}{9},-\dfrac{20}{9} \pi\)
解析 (1) \(\because-1480^{\circ}=-\dfrac{74}{9} \pi=-8 \pi-\dfrac{2}{9} \pi=-10 \pi+\dfrac{16}{9} \pi\),
又 \(\because 0 \leq \dfrac{16}{9} \pi<2 \pi\),
故 \(-1480^{\circ}=\dfrac{16}{9} \pi-2 \times 5 \pi\).
(2)\(∵β\)与\(α\)终边相同,
\(\therefore \beta=\alpha+2 k \pi=\dfrac{16}{9} \pi+2 k \pi\),\(k∈Z\).
又\(∵β∈[-4π,0]\),
\(\therefore \beta_1=\dfrac{16}{9} \pi-2 \pi=-\dfrac{2 \pi}{9}\),\(\beta_2=\dfrac{16}{9} \pi-4 \pi=-\dfrac{20}{9} \pi\). -
答案 (1)\(\dfrac{3 \pi}{2}\); (2)\(20\)
解析 (1)当小轮转动一周时,求大轮转动的周数为\(x\),
则\(45=60x\),即 \(x=\dfrac{3}{4}\),
大轮转动的弧度数 \(\dfrac{3}{4} \times 2 \pi=\dfrac{3 \pi}{2}\);
(2)设大轮的半径为\(R\),则大轮的速度为\(120 \times \dfrac{45}{60}=90(\mathrm{r} / \mathrm{min})\),
所以大轮上每\(1s\)转过的周数为\(\dfrac{90}{60}=1.5\),
大轮上每\(1s\)转过的弧长是\(1.5×2πR=60πcm\),
所以\(R=20\),
故大轮的半径为\(20\). -
答案 \(12 \pi-9 \sqrt{3}\)
解析 \(S_{\text {扇形 } A O B}=\dfrac{1}{2} \times \dfrac{120}{180} \pi \times 6^2=12 \pi\), \(S_{\triangle A O B}=\dfrac{1}{2} \times 6^2 \times \sin 120^{\circ}=9 \sqrt{3}\),
\(\therefore S_{\text {弓形 } A C B}=S_{\text {扇形 } A O B}-S_{\triangle A O B}=12 \pi-9 \sqrt{3}\).
【B组---提高题】
1.已知扇形的周长为\(C\),当该扇形面积取得最大值时,圆心角为( )
A. \(\dfrac{1}{2} r a d\) \(\qquad \qquad \qquad \qquad\) B.\(1rad\) \(\qquad \qquad \qquad \qquad\) C. \(\dfrac{3}{2} r a d\) \(\qquad \qquad \qquad \qquad\) D.\(2rad\)
参考答案
- 答案 \(D\)
解析 设扇形的圆心角大小为\(α(rad)\),半径为\(r\),
根据扇形的面积为\(S_{\text {扇形 }}=\dfrac{1}{2} a r^2\),周长为\(2r+αr=C\),
得到\(r=\dfrac{C}{2+\alpha}\),且\(0<α<2π\),
\(\therefore S_{\text {扇形 }}=\dfrac{1}{2} \alpha\left(\dfrac{C}{2+\alpha}\right)^2=\dfrac{C^2 \alpha}{2 \alpha^2+8 \alpha+8}=\dfrac{C^2}{8+\left(2 \alpha+\dfrac{8}{\alpha}\right)}\),
又\(2 \alpha+\dfrac{8}{\alpha} \geq 2 \sqrt{2 \alpha \cdot \dfrac{8}{\alpha}}=8\),当且仅当\(2 \alpha=\dfrac{8}{\alpha}\),即\(α=2\)时,\(“=”\)成立,
此时\(S_{\text {扇形 }}\)取得最大值为 \(\dfrac{C^2}{16}\),对应圆心角为\(α=2\).
故选:\(D\).


 浙公网安备 33010602011771号
浙公网安备 33010602011771号