3.3.2 抛物线的简单几何性质(1)
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
【基础过关系列】2022-2023学年高二数学上学期同步知识点剖析精品讲义(人教A版2019)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
选择性必修第一册同步巩固,难度2颗星!
基础知识
几何性质
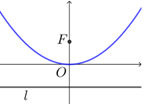
| 标准方程 | $y^2=2px$ | $y^2=-2px$ | $x^2=2py$ | $x^2=-2py$ |
| 图形 | 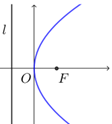
| 
| 
| 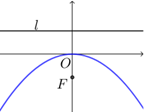 |
| 顶点 | $(0,0)$ | |||
| 对称轴 | $x$轴 | $x$轴 | $y$轴 | $y$轴 |
| 焦点 | $F\left(\dfrac{p}{2}, 0\right)$ | $F\left(-\dfrac{p}{2}, 0\right)$ | $F\left(0, \dfrac{p}{2}\right)$ | $F\left(0,- \dfrac{p}{2}\right)$ |
| 准线方程 | $x=-\dfrac{p}{2}$ | $x= \dfrac{p}{2}$ | $y=-\dfrac{p}{2}$ | $y= \dfrac{p}{2}$ |
| 离心率 | $e=1$ | |||
离心率:抛物线上的点\(M\)与焦点\(F\)的距离和点\(M\)到准线的距离\(d\)的比 \(\dfrac{|M F|}{d}\),叫做离心率.
一些常见结论
① 过抛物线的焦点作垂直于对称轴且交抛物线于\(A\) ,\(B\)两点的线段\(AB\),称为抛物线的“通径”,即\(|AB|=2p\).
证明 抛物线 \(y^2=2px\),设 \(A\left(\dfrac{p}{2}, y_0\right)\),则 \(y_0^2=2 p \cdot \dfrac{p}{2}=p^2\),\(y_0=p\),所以\(|AB|=2p\).
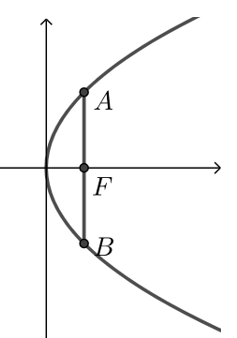
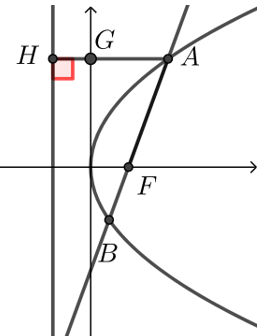
② 若\(A\)、\(B\)在抛物线\(y^2=2px\)上,\(F\)是焦点,则\(A F=x_A+\dfrac{p}{2}\),\(AB=x_A+x_B+p\).
证明 抛物线的定义, \(A F=A H=A G+G H=x_A+\dfrac{p}{2},\),
\(A B=x_A+\dfrac{p}{2}+x_B+\dfrac{p}{2}=x_A+x_B+p\).
基本方法
【题型1】抛物线的简单性质
【典题1】 以原点为顶点,坐标轴为对称轴,并且经过点\(P(-2,-4)\)的抛物线方程是\(\underline{\quad \quad}\) .
解析 ① 当焦点在\(x\)轴上时,设抛物线方程为\(x^2=2py\),
代入\(P(-2,-4)\),\(4=-8p\),解得 \(p=-\dfrac{1}{2}\),所以\(x^2=-y\);
② 当焦点在\(y\)轴上时,设抛物线方程为\(y^2=2px\),
代入\(P(-2,-4)\),\(16=-4p\),解得\(p=-4\),所以\(y^2=-8x\);
点拨 注意抛物线焦点位置.
【典题2】过抛物线\(y^2=4x\)的焦点作直线交抛物线于\(A(x_1,y_1)\),\(B(x_2,y_2)\)两点,若\(|AB|=12\),那么\(x_1+x_2=\)\(\underline{\quad \quad}\) .
解析 由题意,\(p=2\),故抛物线的准线方程是\(x=-1\),
\(∵\)过抛物线\(y^2=4x\)的焦点的直线交抛物线于\(A(x_1,y_1)\),\(B(x_2,y_2)\)两点,
\(∴|AB|=x_1+x_2+2=12\),解得\(x_1+x_2=10\),
故答案为:\(10\).
点拨 若\(A\)、\(B\)在抛物线\(y^2=2px\)上,\(F\)是焦点,则 \(A F=x_A+\dfrac{p}{2}\),\(AB=x_A+x_B+p\).
【典题3】(多选)已知抛物线 \(x^2=\dfrac{1}{2} y\)的焦点为\(F\),\(M(x_1,y_1)\),\(N(x_2,y_2)\)是抛物线上两点,则下列结论正确的是( )
A.点\(F\)的坐标为 \(\left(\dfrac{1}{8}, 0\right)\)
B.若直线\(MN\)过点\(F\),则 \(x_1 x_2=-\dfrac{1}{16}\)
C.若 \(\overrightarrow{M F}=\lambda \overrightarrow{N F}\),则\(|MN|\)的最小值为 \(\dfrac{1}{2}\)
D.若 \(|M F|+|N F|=\dfrac{3}{2}\),则线段\(MN\)的中点\(P\)到\(x\)轴的距离为 \(\dfrac{5}{8}\)
解析 抛物线 \(x^2=\dfrac{1}{2} y\)的焦点为 \(F\left(0, \dfrac{1}{8}\right)\),所以\(A\)不正确;
根据抛物线的性质可得:\(MN\)过\(F\)时,则 \(x_1 x_2=-\dfrac{1}{16}\),所以\(B\)正确;
若 \(\overrightarrow{M F}=\lambda \overrightarrow{N F}\),则\(|MN|\)的最小值为抛物线的通径长,为 \(2 p=\dfrac{1}{2}\),所以\(C\)正确;
抛物线 \(x^2=\dfrac{1}{2} y\)的焦点为 \(F\left(0, \dfrac{1}{8}\right)\),准线方程为 \(y=-\dfrac{1}{8}\),
过点\(M\)、\(N\)、\(P\)分别作准线的垂线\(MM'\),\(NN'\),\(PP'\),
则\(|MM'|=|MF|\),\(|NN'|=|NF|\), \(\left|M M^{\prime}\right|+\left|N N^{\prime}\right|=|M F|+|N F|=\dfrac{3}{2}\),
所以 \(\left|P P^{\prime}\right|=\dfrac{\left|M M^{\prime}\right|+\left|N N^{\prime}\right|}{2}=\dfrac{3}{4}\),

所以线段\(MN\)的中的\(P\)到\(x\)轴的距离为 \(\left|P P^{\prime}\right|-\dfrac{1}{8}=\dfrac{3}{4}-\dfrac{1}{8}=\dfrac{5}{8}\),所以\(D\)正确;
故选:\(BCD\).
【典题4】已知点\(A(0,4)\),抛物线\(C:x^2=2py(0<p<4)\)的准线为\(1\),点\(P\)在\(C\)上,作\(PH⊥l\)于\(H\),且\(|PH|=|PA|\),\(∠APH=120°\),则抛物线方程为\(\underline{\quad \quad}\).
解析 设抛物线的焦点为 \(F\left(0, \dfrac{p}{2}\right)\), \(|A F|=4-\dfrac{p}{2}\),由抛物线的定义可知,\(|PH|=|PF|\),

\(∵|PH|=|PA|\),\(∴|PA|=|PF|\),
不妨设点\(P\)在第一象限,过点\(P\)作\(PQ⊥y\)轴于点\(Q\),
则\(Q\)为\(AF\)的中点, \(|A Q|=|F Q|=\dfrac{1}{2}|A F|=\dfrac{1}{2}\left(4-\dfrac{p}{2}\right)\),
\(∵∠APH=120°\),\(∴∠APQ=120°-90°=30°\),
\(\therefore|P Q|=\sqrt{3}|A Q|=\dfrac{\sqrt{3}}{2}\left(4-\dfrac{p}{2}\right)\), \(|O Q|=|F Q|+|O F|=\dfrac{1}{2}\left(4-\dfrac{p}{2}\right)+\dfrac{p}{2}=2+\dfrac{p}{4}\),
\(∴\)点\(P\)的坐标为 \(\left(\dfrac{\sqrt{3}}{2}\left(4-\dfrac{p}{2}\right), 2+\dfrac{p}{4}\right)\),
\(∵\)点\(P\)在抛物线\(C\)上, \(\therefore\left[\dfrac{\sqrt{3}}{2}\left(4-\dfrac{p}{2}\right)\right]^2=2 p \times\left(2+\dfrac{p}{4}\right)\),
化简得\(5p^2+112p-192=0\),解之得 \(p=\dfrac{8}{5}\)或\(-24\)(舍负),
\(∴\)抛物线方程为 \(x^2=\dfrac{16}{5} y\).
巩固练习
1.顶点在原点,对称轴为\(y\)轴,顶点到准线的距离为\(4\)的抛物线方程是( )
A.\(x^2=16y\) \(\qquad \qquad\) B.\(x^2=8y\) \(\qquad \qquad\) C.\(x^2=±8y\) \(\qquad \qquad\) D .\(x^2=±16y\)
2.已知过点\((0,1)\)的直线与抛物线\(x^2=4y\)交于\(A(x_1,y_1)\),\(B(x_2,y_2)\)两点,若 \(y_1+y_2=\dfrac{9}{4}\),则\(|AB|=\)( )
A. \(\dfrac{25}{4}\) \(\qquad \qquad\) B. \(\dfrac{17}{4}\) \(\qquad \qquad\) C. \(\dfrac{13}{4}\) \(\qquad \qquad\) D. \(\dfrac{9}{4}\)
3.在直角坐标系\(xOy\)中,动圆\(C\)经过点\((0,2)\),且圆心\(C(x_0,y_0)\)在抛物线 \(y=\dfrac{1}{4} x^2\)上.记圆\(C\)被\(x\)轴所截得的弦长为\(|PQ|\),则随着\(y_0\)的增大,\(|PQ|\)的变化情况是( )
A.恒为定值 \(\qquad \qquad\) B.一直减小 \(\qquad \qquad\) C.一直增大 \(\qquad \qquad\) D.先减小,再增大
4.如图,点\(A\)是曲线 \(y=\sqrt{x^2+2}(y \leq 2)\)上的任意一点,\(P(0,-2)\),\(Q(0,2)\),射线\(QA\)交曲线 \(y=\dfrac{1}{8} x^2\)于\(B\)点,\(BC\)垂直于直线\(y=3\),垂足为点\(C\).则下列判断:①\(|AP|-|AQ|\)为定值 \(2 \sqrt{2}\);②\(|QB|+|BC|\)为定值\(5\).其中正确的说法是( )

A.①②都正确 \(\qquad \qquad\) B.①②都错误 \(\qquad \qquad\) C.①正确,②错误 \(\qquad \qquad\) D.①都错误,②正确
5.过抛物线\(y^2=2px\)的焦点\(F\)的直线与抛物线交于\(A\),\(B\)两点,若\(A\),\(B\)在准线上的射影为\(A_1\),\(B_1\),则\(∠A_1 FB_1\)等于\(\underline{\quad \quad}\).
6.设抛物线\(C:y^2=8x\)的焦点为\(F\),\(A\)是\(C\)上的一点且在第一象限,以\(F\)为圆心,以\(FA\)为半径的圆交\(C\)的准线于\(B\),\(D\)两点,且\(A\),
\(F\),\(B\)三点共线,则点\(A\)的横坐标为\(\underline{\quad \quad}\) .
参考答案
-
答案 \(D\)
解析 根据顶点在原点,对称轴为\(y\)轴,可设抛物线方程为\(x^2=±2py\).
\(∵\)顶点到准线的距离为\(4\), \(\therefore \dfrac{p}{2}=4\),\(∴2p=16\),
\(∴\)所求抛物线方程为\(x^2=±16y\).
故选:\(D\). -
答案 \(B\)
解析 由题意可知点\((0,1)\)为抛物线的焦点,
则由抛物线的定义可得 \(|A B|=y_1+y_2+2=\dfrac{9}{4}+2=\dfrac{17}{4}\),
故选:\(B\). -
答案 \(A\)
解析 如图所示,
设\(PQ\)的中点为\(D\),圆心\(C(x_0,y_0)\)在抛物线 \(y=\dfrac{1}{4} x^2\)上,
则 \(|C D|=y_0=\dfrac{1}{4} x_0^2\),
\(\therefore|C P|=|C A|=\sqrt{\left(x_0-0\right)^2+\left(\dfrac{1}{4} x_0^2-2\right)^2}\);
由勾股定理得, \(|P Q|=2|P D|=2 \sqrt{|C P|^2-|C D|^2}=2 \sqrt{x_0^2+\left(\dfrac{1}{4} x_0^2-2\right)^2-\left(\dfrac{1}{4} x_0^2\right)^2}=4\),
\(∴\)圆\(C\)被\(x\)轴所截得的弦长\(|PQ|\)为定值.
故选:\(A\).

-
答案 \(A\)
解析 曲线 \(y=\sqrt{x^2+2}(y \leq 2)\)两边平方,得 \(y^2-x^2=2\),
为双曲线 \(\dfrac{y^2}{2}-\dfrac{x^2}{2}=1\)的 \(\sqrt{2} \leq y \leq 2\)的部分,\(P(0,-2)\),\(Q(0,2)\)恰为该双曲线的两焦点,
由双曲线定义知,\(||AP|-|AQ||=2\sqrt{2}\),
又\(|AP|>|AQ|\),\(∴|AP|-|AQ|=2\sqrt{2}\),①正确;
曲线 \(y=\dfrac{1}{8} x^2\)即抛物线 \(x^2=8y\),其焦点为\(Q(0,2)\),准线方程为\(y=-2\),
过\(B\)作\(BD\)垂直直线\(y=-2\)于\(D\),
由抛物线定义,知\(|QB|+|BC|=|BD|+|BC|=|CD|=5\),②正确;
故选:\(A\).

-
答案 \(90^∘\)
解析 如图,由抛物线定义知\(|AA_1 |=|AF|\),\(|BB_1 |=|BF|\),所以\(∠AA_1 F=∠AFA_1\).

又\(∠AA_1 F=∠A_1 FO\),所以\(∠AFA_1=∠A_1 FO\).
同理\(∠BFB_1=∠B_1 FO\).
于是\(∠AFA_1+∠BFB_1=∠A_1 FO+∠B_1 FO=∠A_1 FB_1\).
故\(∠A_1 FB_1=90^∘\). -
答案 \(6\)
解析 \(∵A\),\(F\),\(B\)三点共线,\(∴AB\)为圆\(F\)的直径,则\(AD⊥BD\).
由抛物线定义知 \(|A D|=|A F|=\dfrac{1}{2}|A B|\),
又抛物线\(C:y^2=8x\)的 \(\dfrac{p}{2}=2\),
\(∴\)在\(Rt△ADB\)中,可得\(|AD|=4|OF|=8\).
设\(A\)的横坐标为\(x_0\),则\(|AD|=x_0+2=8\),
即\(x_0=6\).

【题型2】最值问题
【典题1】 已知点\(P\)是抛物线\(y^2=2x\)上的动点,点\(P\)在\(y\)轴上的射影是\(M\),点 \(A\left(\dfrac{7}{2}, 4\right)\),则\(|PA|+|PM|\)的最小值是 .
解析 依题意可知焦点 \(F\left(\dfrac{1}{2}, 0\right)\),准线 \(x=-\dfrac{1}{2}\),延长\(PM\)交准线于\(H\)点.则\(|PF|=|PH|\)\(\underline{\quad \quad}\).
\(|P M|=|P H|-\dfrac{1}{2}=|P F|-\dfrac{1}{2}\), \(|P M|+|P A|=|P F|+|P A|-\dfrac{1}{2}\),
我们只有求出\(|PF|+|PA|\)最小值即可.
由三角形两边长大于第三边可知,\(|PF|+|PA|⩾|FA|\),
当\(A\),\(P\),\(F\)三点共线时,\(|PF|+|PA|\)可取得最小值\(|FA|=5\).
则所求为 \(|P M|+|P A|=5-\dfrac{1}{2}=\dfrac{9}{2}\).

点拨 本题属于几何法求最值,结合图象与抛物线的定义分析,注意点\(A\)在抛物线外还是抛物线内!
【典题2】已知点\(M(2,0)\),点\(P\)在曲线\(y^2=4x\)上运动,点\(F\)为抛物线的焦点,则 \(\dfrac{|P M|^2}{|P F|-1}\)的最小值为( )
A. \(\sqrt{3}\) \(\qquad \qquad\) B. \(2(\sqrt{5}-1)\) \(\qquad \qquad\) C. \(4 \sqrt{5}\) \(\qquad \qquad\) D.\(4\)
解析 设\(P(x,y)\),可得 \(\dfrac{|P M|^2}{|P F|-1}=\dfrac{(x-2)^2+y^2}{x}=\dfrac{x^2+4}{x}=x+\dfrac{4}{x} \geq 2 \sqrt{x \cdot \dfrac{4}{x}}=4\).
当且仅当\(x=2\)时取得最小值\(4\).
故选:\(D\).
点拨 本题解题思路属于代数法,设元\(P(x,y)\),把 \(\dfrac{|P M|^2}{|P F|-1}\)转化为代数式,再利用基本不等式或函数的方法求其最值.
巩固练习
1.已知点 \(Q(2 \sqrt{2}, 0)\)及抛物线 \(y=\dfrac{x^2}{4}\)上一动点\(P(x_0,y_0 )\),则\(y_0+|PQ|\)的最小值为\(\underline{\quad \quad}\).
2.设\(P\)是抛物线\(y^2=4x\)上的一个动点,若\(B(3,2)\),则\(|PB|+|PF|\)的最小值为 \(\underline{\quad \quad}\) .
3.若点\(A\)为抛物线\(y^2=4x\)上一点,\(F\)是抛物线的焦点,\(|AF|=6\),点\(P\)为直线\(x=-1\)上的动点,则\(|PA|+|PF|\)的最小值为\(\underline{\quad \quad}\) .
4.过点\(Q(2,0)\)的直线与抛物线\(C:y^2=2x\)的一个交点是\(A\),与\(y\)轴交于\(D\)点,且 \(\overrightarrow{D A}=2 \overrightarrow{D Q}\),\(P\)为抛物线\(C\)上一动点,则 \(\overrightarrow{P A} \cdot \overrightarrow{P D}\)的最小值是\(\underline{\quad \quad}\).
参考答案
-
答案 \(2\)
解析 用抛物线的定义:焦点\(F(0,1)\),准线\(y=-1\),
设\(P\)到准线的距离为\(d\),
\(y_0+|PQ|=d-1+|PQ|=|PF|+|PQ|-1⩾|FQ|-1=2\)
(当且仅当\(F,Q,P\)共线时取等号)
故\(y_0+|PQ|\)的最小值是\(2\). -
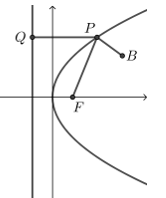
答案 \(4\)
解析 如图, 过点\(B\)作\(BQ\)重直准线于点\(Q\), 交拋物线于点\(P_1\), 则\(|P_1 Q|=|P_1 F|\),
则有\(|PB|+|PF|⩾|P_1 B|+|P_1 Q|=|BQ|=4\), 即\(|PB|+|PF|\)的最小值为\(4\).
-
答案 \(2 \sqrt{21}\)
解析 由题意可知,\(p=2\),\(F(1,0)\),
由抛物线的定义可知, \(|A F|=x_A+\dfrac{p}{2}=x_A+1=6\),\(∴x_A=5\),
代入抛物线方程,得 \(y_A{ }^2=20\),不妨取点\(A\)为 \((5,2 \sqrt{5})\),

设点\(F\)关于\(x=-1\)的对称点为\(E\),则\(E(-3,0)\),
\(\therefore|P A|+|P F|=|P A|+|P E| \geq|A E|=\sqrt{(5+3)^2+(2 \sqrt{5})^2}=2 \sqrt{21}\). -
答案 \(-9\)
解析 由题 \(\overrightarrow{D A}=2 \overrightarrow{D Q}\), \(\therefore \overrightarrow{D Q}=\overrightarrow{Q A}\)
\(∵Q(2,0)\),易知\(A\)点的横坐标为\(4\),
抛物线\(C:y^2=2x\)中,\(x=4\), \(y=\pm 2 \sqrt{2}\),
设 \(A(4,2 \sqrt{2})\),则对应的 \(D(0,-2 \sqrt{2})\).
\(∵P\)为抛物线\(C\)上一动点,设 \(P\left(\dfrac{y_1^2}{2}, y_1\right)\),
\(\overrightarrow{P A}=\left(4-\dfrac{y_1^2}{2}, 2 \sqrt{2}-y_1\right)\), \(\overrightarrow{P D}=\left(-\dfrac{y_1^2}{2},-2 \sqrt{2}-y_1\right)\),
则 \(\overrightarrow{P A} \cdot \overrightarrow{P D}=\left(4-\dfrac{y_1^2}{2}\right)\left(-\dfrac{y_1^2}{2}\right)+\left(2 \sqrt{2}-y_1\right)\left(-2 \sqrt{2}-y_1\right)\)\(=\dfrac{y_1^4}{4}-y_1^2-8=\dfrac{1}{4}\left(y_1^2-2\right)^2-9\).
\(\therefore(\overrightarrow{P A} \cdot \overrightarrow{P D})_{\min }=-9\).
分层练习
【A组---基础题】
1.顶点在原点,关于\(x\)轴对称,并且经过点\(M(-1,2)\)的抛物线方程为( )
A.\(y^2=4x\) \(\qquad \qquad\) B.\(y^2=-4x\) \(\qquad \qquad\) C. \(x^2=\dfrac{1}{2} y\) \(\qquad \qquad\) D. \(x^2=-\dfrac{1}{2} y\)
2.如图过抛物线\(y^2=2px(p>0)\)的焦点F的直线依次交拋物线及准线于点\(A\),\(B\),\(C\),若\(|BC|=2|BF|\),且\(|AF|=3\),则\(p=\)( )

A.\(2\) \(\qquad \qquad\) B. \(\dfrac{3}{2}\) \(\qquad \qquad\) C.\(3\) \(\qquad \qquad\) D.\(6\)
3.设点\(M\)为抛物线\(C:y^2=4x\)的准线上一点(不同于准线与\(x\)轴的交点),过抛物线\(C\)的焦点\(F\),且垂直于\(x\)轴的直线与\(C\)交于\(A\)、\(B\)两点,设\(MA\)、\(MF\)、\(MB\)的斜率分别为\(k_1\) 、\(k_2\)、\(k_3\),则 \(\dfrac{k_1+k_3}{k_2}\)的值为( )
A.\(2\) \(\qquad \qquad\) B. \(2 \sqrt{2}\) \(\qquad \qquad\) C.\(4\) \(\qquad \qquad\) D. \(4 \sqrt{2}\)
4.已知\(F\)为抛物线\(C:x^2=2py(1<p<2)\)的焦点,\(F\)关于原点的对称点为\(F'\),点\(M\)在抛物线\(C\)上,给出下列三个结论:
①使得\(△MFF'\)为等腰三角形的点\(M\)有且仅有\(6\)个:
②使得 \(\left|\overrightarrow{M F^{\prime}}\right|+|\overrightarrow{M F}|=1 \mid\)的点\(M\)有且仅有\(2\)个:
③使得 \(\left|\overrightarrow{M F^{\prime}}\right|=\sqrt{2}|\overrightarrow{M F}|\)点\(M\)有且仅有\(4\)个.
其中正确结论的个数为( )
A.\(0\) \(\qquad \qquad\) B.\(1\) \(\qquad \qquad\) C.\(2\) \(\qquad \qquad\) D.\(3\)
5.(多选)抛物线有如下光学性质:由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出.已知抛物线\(y^2=4x\)的焦点为\(F\),一束平行于\(x\)轴的光线\(l_1\)从点\(M(3,1)\)射入,经过抛物线上的点\(P(x_1,y_1)\)反射后,再经抛物线上另一点\(Q(x_2,y_2)\)反射后,沿直线\(l_2\)射出,则下列结论中正确的是( )
A.\(x_1 x_2=1\) \(\qquad \qquad\) \(\qquad \qquad\) B. \(k_{P Q}=-\dfrac{4}{3}\) \(\qquad \qquad\) C. \(|P Q|=\dfrac{25}{4}\) \(\qquad \qquad\) D.\(l_1\)与\(l_2\)之间的距离为\(4\)
6.设抛物线\(x^2=12y\)的焦点为\(F\),经过点\(P(2,1)\)的直线\(l\)与抛物线相交于\(A\)、\(B\)两点,若点\(P\)恰为线段\(AB\)的中点,则\(|AF|+|BF|=\)\(\underline{\quad \quad}\).
7.已知抛物线\(C:y^2=4x\)的焦点为\(F\),准线为\(l\),\(P\)为\(C\)上一点,\(PQ\)垂直\(l\)于点\(Q\),\(M\),\(N\)分别为\(PQ\),\(PF\)的中点,\(MN\)与\(x\)轴相交于点\(R\),若\(∠NRF=60°\),则\(|FR|\)等于\(\underline{\quad \quad}\).
8.点\(P\)是抛物线\(y^2=4x\)上一动点,则点\(P\)到点\(A(0,-1)\)的距离与点\(P\)到直线\(x=-2\)的距离和的最小值是\(\underline{\quad \quad}\) .
9.已知抛物线\(C:y^2=4x\)的焦点为\(F\),\(M(x_1,y_1)\),\(N(x_2,y_2)\)是抛物线\(C\)上的两个动点,若\(x_1+x_2+2=2|MN|\),则\(∠MFN\)的最大值为\(\underline{\quad \quad}\).
10.已知点\(P\)在抛物线 \(y^2=12x\)上,点\(Q\)在圆 \((x-3)^2+y^2=1\)上,点\(M(6,0)\),令 \(t=\dfrac{|M P|^2}{|P Q|}\),则\(t\)的最小值为\(\underline{\quad \quad}\),此时点\(P\)的横坐标为\(\underline{\quad \quad}\).
参考答案
-
答案 \(B\)
解析 设抛物线解析式为\(y^2=-2px\),
把\((-1,2)\)代入得\(4=2p\),解得\(p=2\),
所以抛物线标准方程为\(y^2=-4x\),
故选:\(B\). -
答案 \(B\)
解析 过\(A\),\(B\)分别作准线的垂线,垂足为\(N\),\(M\),
\(|BC|=2|BF|=2BM\),\(∠MCB=30°\).\(|AF|=3=AN\),\(AC=2AN=6\),
所以\(F\)为\(AC\)的中点, \(p=\dfrac{1}{2} A N=\dfrac{3}{2}\),
故选:\(B\).

-
答案 \(A\)
解析 如图,
由抛物线方程可得,\(F(1,0)\),则\(A(1,-2)\),\(B(1,2)\),
设\(M(-1,m)(m≠0)\),则 \(k_1=\dfrac{m+2}{-2}\), \(k_2=\dfrac{m}{-2}\), \(k_3=\dfrac{m-2}{-2}\).
\(\therefore \dfrac{k_1+k_3}{k_2}=\dfrac{\dfrac{m+2}{-2}+\dfrac{m-2}{-2}}{\dfrac{m}{-2}}=2\).
故选:\(A\).

-
答案 \(A\)
解析 抛物线的焦点 \(F\left(0, \dfrac{p}{2}\right)\),准线方程为 \(y=-\dfrac{p}{2}\),
由\(△MFF'\)为等腰三角形,若\(F'F=MF\),则\(M\)有两个点;
若\(MF'=MF\),则不存在,若\(MF'=FF'\),则\(M\)有两个点,
则使得\(△MFF'\)为等腰三角形的点\(M\)有且仅有\(4\)个,即①错误;
设\(M(m,n)\),可得 \(m^2=2 p n\), \(|M F|=|M K|=n+\dfrac{p}{2}\),
\(\left|\overrightarrow{M F^{\prime}}\right|+|\overrightarrow{M F}|=1\)即为 \(\sqrt{m^2+\left(n+\dfrac{p}{2}\right)^2}+n+\dfrac{p}{2}=1\),
移项平方可得 \(n=\dfrac{1-p}{2+2 p}<0\),与\(n≥0\)矛盾,即②错误;
\(\left|\overrightarrow{M F^{\prime}}\right|=\sqrt{2}|\overrightarrow{M F}|\)即 \(\left|\overrightarrow{M F^{\prime}}\right|=\sqrt{2}|M K|\),可得\(△MKF'\)为等腰直角三角形,
由 \(\left\{\begin{array}{l} |m|=n+\dfrac{p}{2} \\ m^2=2 p n \end{array}\right.\)可得 \(n=\dfrac{p}{2}\),\(m=±p\),可得\(M\)有且只有两个,即③错误.
故选:\(A\).

-
答案 \(ABC\)
解析 如图所示,

由题意可得,点\(P\)的坐标为 \(\left(\dfrac{1}{4}, 1\right)\),点\(Q\)的坐标为\((4,-4)\),
\(∴x_1 x_2=1\),即选项\(A\)正确;
\(\therefore k_{P Q}=\dfrac{-4-1}{4-\dfrac{1}{4}}=-\dfrac{4}{3}\),即选项\(B\)正确;
由抛物线的定义可知, \(|P Q|=x_1+x_2+p=\dfrac{1}{4}+4+2=\dfrac{25}{4}\),即选项\(C\)正确;
\(∵l_1\)与\(l_2\)平行,
\(∴l_1\)与\(l_2\)之间的距离 \(d=\left|y_1-y_2\right|=5\),即选项\(D\)错误;
故选:\(ABC\). -
答案 \(8\)
解析 过点\(A\),\(B\),\(P\)分别作抛物线准线\(y=-3\)的垂线,
垂足为\(C\),\(D\),\(Q\),据抛物线定义,
得\(|AF|+|BF|=|AC|+|BD|=2|PQ|=8\). -
答案 \(2\)
解析 如图所示:连接\(MF\),\(QF\),

\(∵y^2=4x\)的焦点为\(F\),准线为\(l\),\(P\)为\(C\)上一点
\(∴FH=2\),\(PF=PQ\)
\(∵M\),\(N\)分别为\(PQ\),\(PF\)的中点,\(∴MN∥QF\),
\(∵PQ\)垂直\(l\)于点\(Q\),\(∴PQ∥OR\),
\(∴\)四边形\(MQFR\)是平行四边形,\(∴FR=MQ\)
\(∵PQ=PF\),\(∠NRF=60°\),\(∴△PQF\)为等边三角形,
\(∴MF⊥PQ\),
\(∴\)四边形\(MQHF\)是矩形,\(∴MQ=HF=2\)
\(∴FR=MQ=2\),
故答案为:\(2\). -
答案 \(\sqrt{2}+1\)
解析 由题可知,焦点\(F(1,0)\),准线为\(x=-1\),过\(P\)作\(PN⊥\)准线于\(N\),连接\(PF\)、\(AF\),

由抛物线的定义可知,\(|PN|=|PF|\),\(|FA|≤|PA|+|PF|\),
所以当\(P\)为\(AF\)与抛物线的交点时,点\(P\)到点\(A\)的距离与点\(P\)到直线\(x=-1\)的距离之和的最小值为 \(|F A|=\sqrt{2}\),
所以点\(P\)到点\(A\)的距离与\(P\)到直线\(x=-2\)的距离和的最小值是 \(\sqrt{2}+1\). -
答案 \(\dfrac{\pi}{3}\)
解析 如图,依抛物线的定义,可得\(|MF|=x_1+1\),\(|NF|=x_2+1\),
\(∴x_1+x_2+2=2|MN|⇔|MF|+|NF|=2|MN|\),
由余弦定理得 \(\cos \angle M F N=\dfrac{M F^2+N F^2-M N^2}{2 M F \cdot N F}\)\(=\dfrac{M F^2+N F^2-\dfrac{1}{4}(M F+N F)^2}{2 M F \cdot N F}\)
\(=\left(\dfrac{3}{4} M F^2+\dfrac{3}{4} N F^2-\dfrac{1}{2} M F \cdot N F\right) \div 2 M F \cdot N F\)\(\geq \dfrac{\dfrac{3}{2} M F \cdot N F-\dfrac{1}{2} M F \cdot N F}{2 M F \cdot N F}=\dfrac{1}{2}\)
\(\therefore 0<\angle M F N \leq \dfrac{\pi}{3}\),
故答案为: \(\dfrac{\pi}{3}\).

-
答案 \(4 \sqrt{13}-8\), \(2 \sqrt{13}-4\)
解析 如图,

设抛物线的焦点\(F(3,0)\),点\(P(x_0,y_0)\),则\(y_0^2=12x_0\),
\(\therefore|M P|^2=\left(x_0-6\right)^2+y_0^2=x_0^2+36\),
又抛物线的焦点与圆心重合,故要使t取得最小值,则\(|PQ|\)应取最大值,
由抛物线的定义可知, \(|P Q|_{\max }=|P F|+1=x_0+4\),
\(\therefore t=\dfrac{x_0^2+36}{x_0+4}=\dfrac{\left(x_0+4\right)^2-8\left(x_0+4\right)+52}{x_0+4}\)\(=\left(x_0+4\right)+\dfrac{52}{x_0+4}-8 \geq 4 \sqrt{13}-8\),
当且仅当 \(x_0+4=\dfrac{52}{x_0+4}\),即 \(x_0=2 \sqrt{13}-4 \mid\)时,等号成立.
故答案为 \(4 \sqrt{13}-8\), \(2 \sqrt{13}-4\).
【B组---提高题】
1.(多选)已知\(O\)是坐标原点,\(A\),\(B\)是抛物线\(y=x^2\)上不同于\(O\)的两点,且\(OA⊥OB\),下列结论中正确的是( )
A.\(|OA|⋅|OB|≥2\) \(\qquad \qquad \qquad \qquad \qquad \qquad\) B. \(|O A|+|O B| \geq 2 \sqrt{2}\)
C.直线\(AB\)过抛物线\(y=x^2\)的焦点 \(\qquad \qquad\) D.\(O\)到直线\(AB\)的距离小于或等于\(1\)
2.已知抛物线\(C:y^2=2px(p>0)\)的焦点为\(F\),点\(M\),\(N\)在抛物线上,且\(M\),\(N\),\(F\)三点共线点\(P\)在准线上,若 \(\overrightarrow{P N}=\overrightarrow{N M}\),则 \(\dfrac{p}{|M F|}=\)\(\underline{\quad \quad}\).
参考答案
- 答案 \(ABD\)
解析 设\(A(x_1,x_1^2 )\),\(B(x_2,x_2^2 )\),\((x_1≠0,x_2≠0 )\)
\(∵OA⊥OB\), \(\therefore \overrightarrow{O A} \cdot \overrightarrow{O B}=0\),
\(\therefore \overrightarrow{O A} \cdot \overrightarrow{O B}=\left(x_1, x_1^2\right) \cdot\left(x_2, x_2^2\right)=x_1 x_2+x_1^2 x_2^2=x_1 x_2\left(1+x_1 x_2\right)=0\),
\(∴1+x_1 x_2=0\), \(\therefore x_2=-\dfrac{1}{x_1}\),
\(\therefore|O A| \cdot|O B|=\sqrt{\left(x_1{ }^2+x_1^4\right) \cdot\left(x_2{ }^2+x_2^4\right)}=\sqrt{\left(x_1^2+x_1^4\right)\left(\dfrac{1}{x_1{ }^2}+\dfrac{1}{x_1^4}\right)}\) \(=\sqrt{1+x_1^2+\dfrac{1}{x_1^2}+1} \geq \sqrt{2+2 \sqrt{x_1^2 \cdot \dfrac{1}{x_1{ }^2}}}=2\),
当且仅当 \(x_1^2=\dfrac{1}{x_1^2}\),即\(x_1=±1\)时等号成立,故选项\(A\)正确,
又 \(|O A|+|O B| \geq 2 \sqrt{|O A| \cdot|O B|} \geq 2 \sqrt{2}\),故选项\(B\)正确,
\(∵\)直线\(AB\)的斜率为 \(\dfrac{x_2^2-x_1^2}{x_2-x_1}=x_2+x_1=x_1-\dfrac{1}{x_1}\) ,
\(∴\)直线\(AB\)的方程为 \(y-x_1^2=\left(x_1-\dfrac{1}{x_1}\right)\left(x-x_1\right)\),
当\(x=0\)时,\(y=1\),焦点坐标 \(\left(0, \dfrac{1}{4}\right)\)不满足直线\(AB\)的方程,故选项\(C\)错误,
原点\((0,0)\)到直线 \(A B:\left(x_1-\dfrac{1}{x_1}\right) x-y+1=0\)的距离 \(d=\dfrac{1}{\sqrt{\left(x_1-\dfrac{1}{x_1}\right)^2+1^2}} \leq 1\),故选项\(D\)正确,
故选:\(ABD\). - 答案 \(\dfrac{2}{3}\)
解析 如图,

分别过\(M\),\(N\)作\(ME\),\(NG\)垂直于抛物线的准线于\(E\),\(G\),
由 \(\overrightarrow{P N}=\overrightarrow{N M}\),得\(PN=NM\),
由抛物线定义可知\(NF=NG\),\(FM=ME\),
再由\(△PNG∽△PME\),得 \(\dfrac{P N}{N G}=\dfrac{P N}{N F}=\dfrac{P M}{M E}=\dfrac{P M}{M F}\),
\(\therefore \dfrac{P N}{N F}=\dfrac{P M}{M F}\),即 \(\dfrac{M F}{P M}=\dfrac{N F}{P N}=\dfrac{N F}{\dfrac{1}{2} P M}\),
\(∴MF=2NF\),则 \(N F=\dfrac{1}{3} N M=\dfrac{1}{6} P M\), \(P F=P N+N F=\dfrac{1}{2} P M+\dfrac{1}{6} P M=\dfrac{2}{3} P M\).
\(\therefore \dfrac{p}{|M F|}=\dfrac{F K}{M E}=\dfrac{P F}{P M}=\dfrac{2}{3}\).
故答案为: \(\dfrac{2}{3}\).
【C组---拓展题】
1.已知抛物线\(C\)的顶点为坐标原点,焦点\(F\)在\(x\)轴上,其准线为\(l\),过\(F\)的直线交抛物线于\(M\),\(N\)两点,作\(MS⊥l\),\(NT⊥l\),垂足分别为\(S\),\(T\).若 \(\overrightarrow{M F}=3 \overrightarrow{F N}\),且\(△STF\)的面积为 \(\dfrac{8 \sqrt{3}}{3}\),则抛物线\(C\)的方程为( )
A.\(y^2=±x\) \(\qquad \qquad\) B.\(y^2=±2x\) \(\qquad \qquad\) C.\(y^2=±3x\) \(\qquad \qquad\) D.\(y^2=±4x\)
2.若点\(P\)是曲线\(C_1:y2=16x\)上的动点,点\(Q\)是曲线\(C_2:(x-4)^2+y^2=9\)上的动点,点\(O\)为坐标原点,则 \(| \dfrac{P Q}{O P} \mid\)的最小值是\(\underline{\quad \quad}\).
参考答案
-
答案 \(D\)
解析 如图所示,过点\(N\)作\(NH∥l\)交直线\(MS\)于点\(H\),交\(x\)轴于点\(P\).

设点\(M(x_1,y_1)\)、\(N(x_2,y_2)\),
当焦点在\(x\)轴的正半轴时,设抛物线\(C:y^2=2px(p>0)\),
\(\because \overrightarrow{M F}=3 \overrightarrow{F N}\),且 \(F\left(\dfrac{p}{2}, 0\right)\),
\(\therefore\left(\dfrac{p}{2}-x_1,-y_1\right)=3\left(x_2-\dfrac{p}{2}, y_2\right)\),
\(\therefore \dfrac{p}{2}-x_1=3\left(x_2-\dfrac{p}{2}\right) \Rightarrow x_1+3 x_2=2 p\) ①
\(\therefore-y_1=3 y_2 \Rightarrow y_1^2=9 y_2^2 \Rightarrow 2 p x_1=18 p x_2 \Rightarrow x_1=9 x_2\) ②.
由①②可解得 \(x_1=\dfrac{3 p}{2}\), \(x_2=\dfrac{p}{6}\).
\(\therefore y_1^2=2 p x_1=3 p^2 \Rightarrow y_1=\sqrt{3} p\); \(y_2^2=2 p x_2=\dfrac{p^2}{3} \Rightarrow y_2=-\dfrac{\sqrt{3}}{3} p\),
\(\therefore|S T|=y_1-y_2=\dfrac{4 \sqrt{3}}{3} p\)
\(\therefore S_{\triangle S T F}=\dfrac{1}{2} \cdot \dfrac{4 \sqrt{3}}{3} p \cdot p=\dfrac{8 \sqrt{3}}{3}\),解得\(p=2\),
此时抛物线\(C\)的方程为\(y^2=4x\).
同理,当焦点在\(x\)轴的负半轴时,可得\(p=-2\),此时抛物线\(C\)的方程为\(y^2=-4x\).
综上所述,抛物线\(C\)的方程为\(y^2=±4x\).
故选:\(D\). -
答案 \(\dfrac{\sqrt{15}}{8}\)
解析 设\(P\)的坐标\((x,y)\),由抛物线的方程\(y^2=16x\),
可得焦点\(F(4,0)\),恰好为圆 \((x-4)^2+y^2=9\)的圆心,
因为\(P\)在抛物线上,所以 \(|O P|=\sqrt{x^2+y^2}=\sqrt{x^2+16 x}\),
\(|PQ|\)的最小值为\(P\)到圆心的距离减半径\(3\),即\(P\)到准线的距离减\(3\),
所以\(|PQ|=x+4-3=x+1\),
所以 \(\left|\dfrac{P Q}{O P}\right|=\dfrac{x+1}{\sqrt{x^2+16 x}}\),设\(t=x+1\),\(x=t-1\),
所以 \(\left|\dfrac{P Q}{O P}\right|=\sqrt{\dfrac{t^2}{(t-1)^2+16(t-1)}}=\sqrt{\dfrac{1}{-\dfrac{15}{t^2}+\dfrac{14}{t}+1}}\),令 \(a=\dfrac{1}{t}\),
\(\sqrt{\dfrac{1}{-\dfrac{15}{t^2}+\dfrac{14}{t}+1}}=\sqrt{\dfrac{1}{-15 a^2+14 a+1}}=\sqrt{\dfrac{1}{-15\left(a-\dfrac{7}{15}\right)^2+\dfrac{64}{15}}}\) ,
当 \(a=\dfrac{7}{15}\)时, \(\left|\dfrac{P Q}{O P}\right|\)最小,且为\(\dfrac{\sqrt{15}}{8}\),
所以 \(\left|\dfrac{P Q}{O P}\right|\)的最小值为 \(\dfrac{\sqrt{15}}{8}\).


 浙公网安备 33010602011771号
浙公网安备 33010602011771号