3.2.2 双曲线的简单几何性质(2)
${\color{Red}{欢迎到学科网下载资料学习 }}$
【基础过关系列】2022-2023学年高二数学上学期同步知识点剖析精品讲义(人教A版2019)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
选择性必修第一册同步巩固,难度3颗星!
基础知识
直线与双曲线的位置关系
设直线\(l:Ax+By+C=0\),双曲线\(C:f(x,y)=0\),把两者方程联立得到方程组,消元\(y(\)或\(x)\)得到一个关于\(x(\)或\(y)\)的方程 \(ax^2+bx+c=0\)(或 \(ay^2+by+c=0\)).
① 当\(a≠0\)时,
\(∆>0⇔\)方程有两个不同的实数解,即直线与双曲线有两个交点\(⇔\)相交;
\(∆=0⇔\)方程有两个相同的实数解,即直线与双曲线有一个交点\(⇔\)相切;
\(∆<0⇔\)方程无实数解,即直线与双曲线无交点\(⇔\)相离.
② 当\(a=0\),\(b≠0\)时,即得到一个一次方程,则只有一个交点,此时直线\(l\)与双曲线的渐*线*行.
直线与圆锥曲线的弦长公式
(1)直线\(y=kx+b\)与双曲线相交于\(A(x_1,y_1 )\),\(B(x_2,y_2)\),则
\(A B=\sqrt{1+k^2} \cdot\left|x_1-x_2\right|=\sqrt{1+k^2} \cdot \sqrt{\left(x_1+x_2\right)^2-4 x_1 x_2}=\sqrt{1+k^2} \cdot \dfrac{\sqrt{\Delta}}{|a|}\)
或
\(A B=\sqrt{1+\dfrac{1}{k^2}} \cdot\left|y_1-y_2\right|=\sqrt{1+\dfrac{1}{k^2}} \cdot \sqrt{\left(y_1+y_2\right)^2-4 y_1 y_2}=\sqrt{1+\dfrac{1}{k^2}} \cdot \dfrac{\sqrt{\Delta}}{|a|}\),
(\(∆=b^2-4ac\),注意对公式推导的理解,其本质是两点距离公式)
中点弦
① 涉及到中点弦问题可用点差法求解,在处理双曲线的中点弦问题要注意检验!
② “点差法”的常见题型:求中点弦方程、求(过定点、*行弦)弦中点轨迹、垂直*分线问题.
双曲线常见的结论
(选学内容,证明可见另一专题《圆锥曲线常见二级结论》)
(1)双曲线点\(P\)处的切线\(PT\)*分\(△PF_1 F_2\)在点\(P\)处的内角.
\(\qquad\)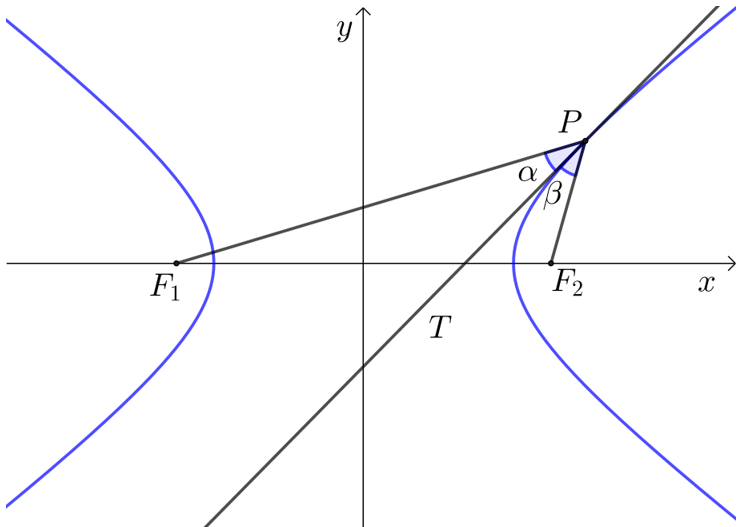
(2) 双曲线 \(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)的焦半径公式:
\(\qquad\)当\(M(x_0,y_0)\)在右支上时, \(MF_1=ex_0+a\), \(MF_2=ex_0-a\).
\(\qquad\)当\(M(x_0,y_0)\)在左支上时, \(MF_1=-ex_0+a\), \(MF_2=-ex_0-a\).
(3) \(AB\)是双曲线 \(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)的不*行于对称轴的弦, \(M(x_0,y_0)\)为\(AB\)的中点,
\(\qquad\)则 \(k_{O M} \cdot k_{A B}=\dfrac{b^2}{a^2}\),即 \(k_{A B}=\dfrac{b^2 x_0}{a^2 y_0}\).
(4) 已知双曲线\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\),\(O\)为坐标原点,\(P\)、\(Q\)为双曲线上两动点,且\(OP⊥OQ\).
\(\qquad\)(i) \(\dfrac{1}{O P^2}+\dfrac{1}{O Q^2}=\dfrac{1}{a^2}-\dfrac{1}{b^2}\) ; \(\qquad \qquad\) (ii) \(O P^2+O Q^2\)的最小值为 \(\dfrac{4 a^2 b^2}{b^2-a^2}\)(或\(\dfrac{4 a^2 b^2}{a^2-b^2}\)).
(5) 若\(P_0 (x_0,y_0)\)在双曲线\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)上,则过\(P_0\)的双曲线的切线方程是 \(\dfrac{x_0 x}{a^2}-\dfrac{y_0 y}{b^2}=1\).
(6) 过双曲线\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)上任意一点\(P\)(不是其顶点)作椭圆切线\(PA\),则有\(k_{P A} \cdot k_{O P}=e^2-1\) .
(7) 过直线\(mx+ny=1(m≠0)\)且在双曲线\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)外一点\(M\)向双曲线引两条切线,切点分别为\(A\),\(B\),
\(\qquad\)则直线\(AB\)必过定点 \(N\left(m a^2, n b^2\right)\).
基本方法
【题型1】直线与双曲线的位置关系与弦长问题
【典题1】已知双曲线 \(x^2-\dfrac{y^2}{4}=1\),过点\(P(1,1)\)的直线\(l\)与双曲线只有一个公共点,求直线\(l\)的方程.
解析 方法1 代数法
(1)当直线\(l\)的斜率不存在时,直线\(l\)的方程为\(x=1\),与双曲线 \(x^2-\dfrac{y^2}{4}=1\)只有一个交点,满足题意;
(2)当直线\(l\)的斜率存在时,设直线\(l\)方程为\(y=k(x-1)+1\),
联立方程得 \(\left\{\begin{array}{c}
y=k(x-1)+1 \\
x^2-\dfrac{y^2}{4}=1
\end{array}\right.\)得 \((4-k^2 ) x^2+(2k^2-2k)x-k^2+2k-5=0 (*)\),
(i)当\(4-k^2=0\)时,\(k=±2\),方程\((*)\)变成\(4x-5=0\)或\(12x-13=0\),方程只有一个根,
即直线\(l\)与双曲线只有一个交点,满足题意,
此时直线\(l\)的方程为\(2x-y-1=0\)或\(2x+y-3=0\);
(ii) 当\(4-k^2≠0\),即\(k≠±2\)时,要满足题意则要\(△=0\),解得 \(k=\dfrac{5}{2}\),
此时直线方程为 \(y=\dfrac{5}{2} x-\dfrac{3}{2}\),即\(5x-2y-3=0\).
综上所述,直线\(l\)的方程为\(x=1\)或\(2x-y-1=0\)或\(2x+y-3=0\)或\(5x-2y-3=0\).
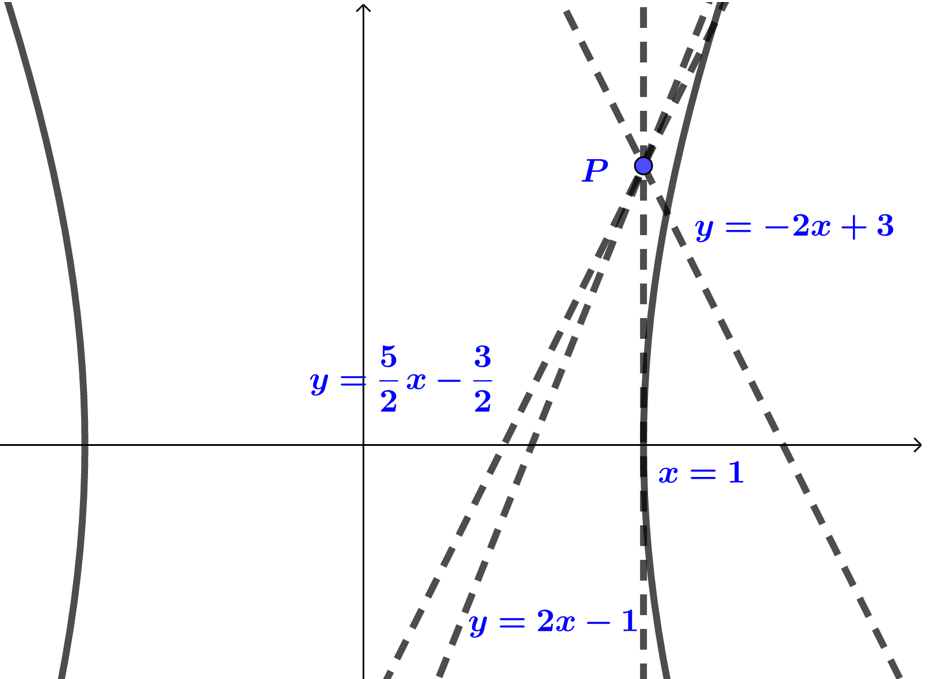
方法2 几何法
双曲线 \(x^2-\dfrac{y^2}{4}=1\)的渐*线方程为\(y=±2x\),
(1)直线\(l:x=1\)与双曲线只有一个公共点;
(2) 直线\(l\)*行于渐*线\(y=±2x\)时,直线\(l\)与双曲线只有一个公共点,
方程为\(y-1=±2(x-1)\),即\(2x-y-1=0\)或\(2x+y-3=0\);
(3) 直线\(l\)不*行于渐*线\(y=±2x\)时,设过\(P\)的直线方程为\(y-1=k(x-1)\),\((k≠±2)\)
由 \(\left\{\begin{array}{c}
y=k(x-1)+1 \\
x^2-\dfrac{y^2}{4}=1
\end{array}\right.\)得 \((4-k^2 ) x^2+(2k^2-2k)x-k^2+2k-5=0\),
只有一个交点,即\(△=0\),解得 \(k=\dfrac{5}{2}\),
此时直线方程为 \(y=\dfrac{5}{2} x-\dfrac{3}{2}\),即\(5x-2y-3=0\).
故直线\(l\)的方程为\(x=1\)或\(2x-y-1=0\)或\(2x+y-3=0\)或\(5x-2y-3=0\).
点拨 从几何的角度看,直线与双曲线\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)的位置关系与渐*线 \(y=\dfrac{b}{a} x\)有关,
(1) 当点\(P\)在双曲线上或内,
当 \(k=\dfrac{b}{a}\)或 \(k=-\dfrac{b}{a}\)时,只有\(1\)个交点;当 \(k \neq \pm \dfrac{b}{a}\)时,只有\(2\)个交点;
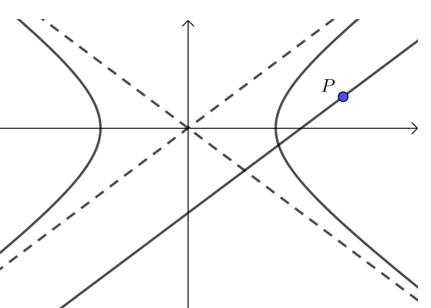
(2) 当点\(P\)在双曲线外,
当 \(k=\dfrac{b}{a}\)或 \(k=-\dfrac{b}{a}\)时,只有\(0\)或\(1\)个交点;
当 \(k>\dfrac{b}{a}\)或 \(k<-\dfrac{b}{a}\)时,只有\(0\)或\(2\)个交点;
当 \(0<k<\dfrac{b}{a}\)或 \(-\dfrac{b}{a}<k<0\)时,只有\(2\)个交点.
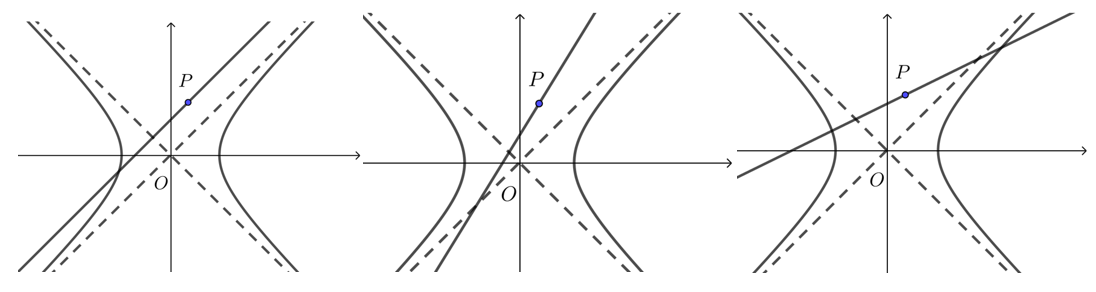
做题时注意特殊情况:斜率\(k\)不存在的直线.
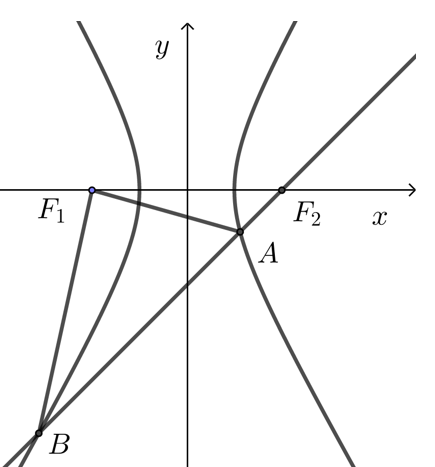
【典题2】已知双曲线\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)的离心率为\(2\),焦点到渐*线的距离等于\(\sqrt{3},\),过右焦点\(F_2\)的直线\(l\)交双曲线于\(A\)、\(B\)两点,\(F_1\)为左焦点.
(1) 求双曲线的方程;
(2) 若\(△F_1 AB\)的面积等于 \(6 \sqrt{2}\),求直线\(l\)的方程.
解析 (1)\(∵\)双曲线\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)的渐*线方程为\(bx±ay=0\),
\(∴\)双曲线焦点\((±c,0)\)到渐*线的距离为 \(\dfrac{|b c|}{\sqrt{b^2+a^2}}=b=\sqrt{3}\),
又\(∵\)双曲线离心率 \(e=\dfrac{c}{a}=2\)
\(∴c=2a\),*方得 \(c^2=a^2+b^2=a^2+3=4a^2\),解得\(a=1\),
因此双曲线的方程为 \(x^2-\dfrac{y^2}{3}=1\).
(2) 方法1 设\(A(x_1,y_1 )\),\(B(x_2,y_2 )\),
当直线\(l\)的斜率不存在,则直线\(l\)的方程\(x=2\),此时易得 \(S_{\triangle F_1 A B}=12 \neq 6 \sqrt{2}\),
故可设直线\(l\)的方程为\(y=k(x-2)\)
由 \(\left\{\begin{array}{c}
y=k(x-2) \\
x^2-\dfrac{y^2}{3}=1
\end{array}\right.\),消元得 \((k^2-3) x^2-4k^2 x+4k^2+3=0\),
\(∵\)有两个交点, \(\therefore k \neq \pm \sqrt{3}\),且 \(x_1+x_2=\dfrac{4 k^2}{k^2-3}\), \(x_1 x_2=\dfrac{4 k^2+3}{k^2-3}\),
\(\therefore|A B|=\sqrt{1+k^2} \cdot \sqrt{\left(x_1+x_2\right)^2-4 x_1 x_2}=\sqrt{1+k^2} \cdot \dfrac{6 \sqrt{k^2+1}}{k^2-3}=\dfrac{6\left(k^2+1\right)}{k^2-3}\),
\(∵F_1 (-2,0)\)到直线\(l\)的距离为: \(d=\dfrac{4|k|}{\sqrt{1+k^2}}\),
\(∴△F_1 AB\)的面积 \(S=\dfrac{1}{2} \cdot d \cdot|A B|=\dfrac{1}{2} \cdot \dfrac{4|k|}{\sqrt{1+k^2}} \cdot \dfrac{6\left(k^2+1\right)}{k^2-3}=12|k| \cdot \dfrac{\sqrt{k^2+1}}{k^2-3}=6 \sqrt{2}\),
\(∴k^4+8k^2-9=0\),解得\(k=±1\),
\(∴\)所以直线\(l\)的方程为\(y=±(x-2)\).
方法2 设\(A(x_1,y_1 )\),\(B(x_2,y_2 )\),
同方法1可得: \(k \neq \pm \sqrt{3}\),且 \(x_1+x_2=\dfrac{4 k^2}{k^2-3}\), \(x_1 x_2=\dfrac{4 k^2+3}{k^2-3}\),
\(∴y_1-y_2=k(x_1-x_2)\),
\(∴△F_1 AB\)的面积 \(S=\dfrac{1}{2}\left|F_1 F_2\right|\left|y_1-y_2\right|=2|k|\left|x_1-x_2\right|\)\(=2|k| \dfrac{\sqrt{\left(4 k^2\right)^2-4\left(k^2-3\right)\left(4 k^2+3\right)}}{\left|k^2-3\right|}=12|k| \dfrac{\sqrt{k^2+1}}{\left|k^2-3\right|}=6 \sqrt{2}\),
两边去分母并且*方整理,得 \(k^4+8k^2-9=0\),解之得\(k^2=1\),
\(∴k=±1\),得直线\(l\)的方程为\(y=±(x-2)\).
点拨
1.过一定点设直线方程为\(y=kx+m\),但要注意斜率是否存在,也设直线方程为\(x=ty+m\);
2.求三角形面积可以用 \(S_{\triangle}=\dfrac{1}{2} \cdot A B \cdot d\)_,_其中\(AB\)为弦长,\(d\)为\(F_2\)到直线\(AB\)的距离;或用\(S_△= \dfrac{1}{2}\left|F_1 F_2\right|\left|y_1-y_2\right|\).
巩固练习
1.双曲线 \(x^2-y^2=1\)与直线\(x-y=1\)交点的个数为( )
A.\(0\) \(\qquad \qquad\) B.\(1\) \(\qquad \qquad\) C.\(2\) \(\qquad \qquad\) D.\(4\)
2.已知双曲线 \(\dfrac{x^2}{12}-\dfrac{y^2}{4}=1\)的右焦点为\(F\),若过点\(F\)的直线与双曲线的右支有且只有一个交点,则该直线斜率的取值范围是( )
A. \(\left(-\dfrac{\sqrt{3}}{3}, \dfrac{\sqrt{3}}{3}\right)\) \(\qquad \qquad\) B. \((-\sqrt{3}, \sqrt{3})\) \(\qquad \qquad\) C. \(\left[-\dfrac{\sqrt{3}}{3}, \dfrac{\sqrt{3}}{3}\right]\) \(\qquad \qquad\) D. \([-\sqrt{3}, \sqrt{3}]\)
3.已知双曲线 \(C:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)的离心率为 \(\sqrt{5}\),虚轴长为\(4\).
(1)求双曲线的标准方程;
(2)过点\((0,1)\),倾斜角为\(45°\)的直线\(l\)与双曲线\(C\)相交于\(A\)、\(B\)两点,\(O\)为坐标原点,求\(∆OAB\)的面积.
4.已知双曲线 \(C:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)的右焦点\(F(2,0)\),一条渐*线的倾斜角为 \(30^∘\).
(1)求双曲线\(C\)的方程;
(2)经过点\(F\)的直线与双曲线的右支交于\(A\),\(B\)两点,与\(y\)轴交于\(P\)点,点\(P\)关于原点的对称点为点\(Q\),求证: \(S_{\triangle Q A B}>\dfrac{4 \sqrt{3}}{3}\).
参考答案
- 答案 \(B\)
解析 联立方程可得 \(\left\{\begin{array}{l} x^2-y^2=1 \\ x-y=1 \end{array}\right.\),消\(y\)可得 \(x^2-(x-1)^2=1\),
即\(2x-1=1\),故\(x=1\),
故方程组有且只有一组解,
故双曲线 \(x^2-y^2=1\)与直线\(x-y=1\)有且只有一个交点;
故选:\(B\). - 答案 \(C\)
解析 渐*线方程 \(y=\pm \dfrac{\sqrt{3}}{3} x\),
当过焦点的两条直线与两条渐*线*行时,
这两条直线与双曲线右支分别只有一个交点(因为双曲线正在与渐*线无限接*中),
那么在斜率是 \(\left[-\dfrac{\sqrt{3}}{3}, \dfrac{\sqrt{3}}{3}\right]\)两条直线之间的所有直线中,
都与双曲线右支只有一个交点.
此直线的斜率的取值范围 \(\left[-\dfrac{\sqrt{3}}{3}, \dfrac{\sqrt{3}}{3}\right]\).
故选:\(C\). - 答案 (1) \(x^2-\dfrac{y^2}{4}=1\) (2) \(\dfrac{4}{3}\)
解析 (1)依题意可得 \(\left\{\begin{array}{c} \dfrac{c}{a}=\sqrt{5} \\ 2 b=4 \\ c^2=a^2+b^2 \end{array}\right.\) ,解得\(a=1\),\(b=2\), \(c=\sqrt{5}\),
\(∴\)双曲线的标准方程为 \(x^2-\dfrac{y^2}{4}=1\).
(2)直线\(l\)的方程为\(y=x+1\),
设\(A(x_1,y_1)\),\(B(x_2,y_2)\),
由 \(\left\{\begin{array}{c} y=x+1 \\ x^2-\dfrac{y^2}{4}=1 \end{array}\right.\)可得\(3x^2-2x-5=0\),
由韦达定理可得 \(x_1+x_2=\dfrac{2}{3}, x_1 x_2=-\dfrac{5}{3}\)
即 \(|A B|=\sqrt{1+k^2} \cdot \sqrt{\left(x_1+x_2\right)^2-4 x_1 x_2}=\sqrt{2} \cdot \sqrt{\dfrac{4}{9}+\dfrac{20}{3}}=\dfrac{8 \sqrt{2}}{3}\)
原点到直线\(l\)的距离为 \(d=\dfrac{\sqrt{2}}{2}\),
于是 \(S_{\triangle O A B}=\dfrac{1}{2} \cdot|A B| \cdot d=\dfrac{1}{2} \cdot \dfrac{8 \sqrt{2}}{3} \cdot \dfrac{\sqrt{2}}{2}=\dfrac{4}{3}\),
\(∴∆OAB\)的面积为 \(\dfrac{4}{3}\). - 答案 (1) \(\dfrac{x^2}{3}-y^2=1\) (2)略
解析 (1)由题意得\(c=2\), \(\dfrac{b}{a}=\tan 30^{\circ}=\dfrac{\sqrt{3}}{3}\),\(c^2=a^2+b^2\)
解得 \(a^2=3\),\(b^2=1\)
所以双曲线\(C\)的方程为 \(\dfrac{x^2}{3}-y^2=1\).
(2)证明:由题意知直线的斜率存在,设直线方程为\(y=k(x-2)\),得\(P(0,-2k)\),\(Q(0,2k)\),
设\(A(x_1,y_1 )\),\(B(x_2,y_2 )\),
联立 \(\left\{\begin{array}{l} \dfrac{x^2}{3}-y^2=1 \\ y=k(x-2) \end{array}\right.\),整理可得 \((3k^2-1) x^2-12k^2 x+12k^2+3=0\),
\(x_1+x_2=\dfrac{12 k^2}{3 k^2-1}\), \(x_1 \cdot x_2=\dfrac{12 k^2+3}{3 k^2-1}\),
所以 \(S_{\triangle Q A B}=\left|S_{\triangle Q P B}-S_{\triangle Q P A}\right|=\dfrac{1}{2}\left|P Q \| x_1-x_2\right|=2|k|\left|x_1-x_2\right|\)
所以 \(S_{\triangle Q A B}^2=4 k^2\left[\left(x_1+x_2\right)^2-4 x_1 x_2\right]\)\(=4 k^2\left[\left(\dfrac{12 k^2}{3 k^2-1}\right)^2-\dfrac{4\left(12 k^2+3\right)}{3 k^2-1}\right]=\dfrac{48 k^2\left(k^2+1\right)}{\left(3 k^2-1\right)^2}\),
直线与双曲线右支有两个交点,
所以 \(x_1+x_2=\dfrac{12 k^2}{3 k^2-1}>0\), \(x_1 \cdot x_2=\dfrac{12 k^2+3}{3 k^2-1}>0\)
所以\(3k^2>1\),
设\(t=3k^2-1>0\),
\(S_{\triangle Q A B}^2=48 \dfrac{\dfrac{(t+1)}{3} \cdot\left(\dfrac{t+1}{3}+1\right)}{t^2}=\dfrac{16}{3}\left(\dfrac{4}{t^2}+\dfrac{5}{t}+1\right)=\dfrac{64}{3}\left(\dfrac{1}{t}+\dfrac{5}{8}\right)^2-3\)\(>\dfrac{64}{3} \times \dfrac{25}{64}-3=\dfrac{16}{3}\),
所以 \(S_{\triangle Q A B}>\dfrac{4 \sqrt{3}}{3}\).
【题型2】直线与双曲线的综合题型
【典题1】 动点\(M(x,y)\)与定点\(F(4,0)\)的距离和\(M\)到定直线 \(l:x=\dfrac{9}{4}\)的距离的比是常数 \(\dfrac{4}{3}\),求动点\(M\)的轨迹,
解析 如图,设\(d\)是点\(M\)直线 \(l:x=\dfrac{9}{4}\)的距离,
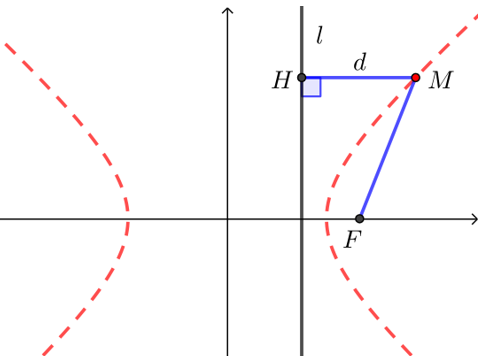
根据题意,得 \(\dfrac{\sqrt{(x-4)^2+y^2}}{\left|x-\dfrac{9}{4}\right|}=\dfrac{4}{3}\),化简得 \(7x^2-9y^2=63\),即 \(\dfrac{x^2}{9}-\dfrac{y^2}{7}=1\),
所以动点\(M\)的轨迹是焦点在\(x\)轴上,实轴长为\(6\)、虚轴长为 \(2 \sqrt{7}\)的双曲线.
点拨 这是双曲线的第二定义,其中直线 \(l:x=\dfrac{9}{4}\)叫做准线,距离之比 \(\dfrac{4}{3}\)为双曲线离心率.
【典题2】已知双曲线\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)渐*线方程为 \(y=\pm \sqrt{3} x\),\(O\)为坐标原点,点 \(M(-\sqrt{3}, \sqrt{3})\)在双曲线上.
(1)求双曲线的方程;
(2)已知\(P\),\(Q\)为双曲线上不同两点,点\(O\)在以\(PQ\)为直径的圆上,求 \(\dfrac{1}{|O P|^2}+\dfrac{1}{|O Q|^2}\)的值.
解析 (1)∵\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)渐*线方程为 \(y=\pm \sqrt{3} x\),
\(∴\)设双曲线方程为 \((y+\sqrt{3} x)(y-\sqrt{3} x)=\lambda\),\(λ≠0\),即 \(y^2-3x^2=λ\),
\(∵O\)为坐标原点,点 \(M(-\sqrt{3}, \sqrt{3})\)在双曲线上,
\(\therefore(\sqrt{3})^2-3(-\sqrt{3})^2=\lambda\),解得\(λ=-6\),
\(∴\)双曲线方程为 \(y^2-3x^2=-6\),即 \(\dfrac{x^2}{2}-\dfrac{y^2}{6}=1\),
(2)\(∵\)直线\(l\)与双曲线交于\(P\)、\(Q\)两点,以弦\(PQ\)为直径的圆经过原点\(O\),
\(∴OP⊥OQ\),
设直线\(OP\)的方程为\(y=kx,(k≠0)\)
代入 \(\lambda^{x^2}-\dfrac{y^2}{6}=1\)中,得 \(\left\{\begin{array}{l}
x^2=\dfrac{6}{3-k^2} \\
y^2=\dfrac{6 k^2}{3-k^2}
\end{array}\right.\),
\(\therefore|O P|^2=x^2+y^2=\dfrac{6\left(k^2+1\right)}{3-k^2}\),同理,得 \(|O Q|^2=\dfrac{6\left(k^2+1\right)}{3 k^2-1}\),
\(\therefore \dfrac{1}{|O P|^2}+\dfrac{1}{|O Q|^2}=\dfrac{1}{3}\) .
点拨 这是定值问题,引入变量表示所求量,最后确定所求值与变量无关,这是常见解题思路.比如本题用\(k\)表示 \(|O P|^2\)与 \(|O Q|^2\),最后通过运算确定 \(\dfrac{1}{|O P|^2}+\dfrac{1}{|O Q|^2}\)的值与\(k\)无关.
【典题3】已知双曲线\(C\)过点 \((4, \sqrt{3})\),且渐*线方程为 \(y=\pm \dfrac{1}{2} x\),直线\(l\)与曲线\(C\)交于点\(M\)、\(N\)两点.
(1)求双曲线\(C\)的方程;
(2)若直线\(l\)过点\((1,0)\),问在\(x\)轴上是否存在定点\(Q\),使得 \(\overrightarrow{Q M} \cdot \overrightarrow{Q N}\)为常数?若存在,求出点坐标及此常数的值;若不存在,说明理由.
解析 (1)因为双曲线\(C\)过点 \((4, \sqrt{3})\),且渐*线方程为 \(y=\pm \dfrac{1}{2} x\),
所以 \(\left\{\begin{array}{l}
\dfrac{16}{a^2}-\dfrac{3}{b^2}=1 \\
\dfrac{b}{a}=\dfrac{1}{2}
\end{array}\right.\),解得 \(b^2=1\),\(a^2=4\)
所以双曲线的方程为 \(\dfrac{x^2}{4}-y^2=1\).
(2)设直线\(l\)的方程为\(x=my+1\),设定点\(Q(t,0)\),
联立方程组 \(\left\{\begin{array}{l}
\dfrac{x^2}{4}-y^2=1 \\
x=m y+1
\end{array}\right.\),消\(x\)可得\((m^2-4) y^2+2my-3=0\),
所以 \(m^2-4≠0\),且 \(△=4m^2+12(m^2-4)>0\),解得 \(m^2>3\)且\(m^2≠4\).
设\(M(x_1,y_1 )\),\(N(x_2,y_2 )\),
所以 \(y_1+y_2=-\dfrac{2 m}{m^2-4}\), \(y_1 y_2=-\dfrac{3}{m^2-4}\),
所以 \(x_1+x_2=m\left(y_1+y_2\right)+2=-\dfrac{2 m^2}{m^2-4}+2=\dfrac{-8}{m^2-4}\)
\(x_1 x_2=\left(m y_1+1\right)\left(m y_2+1\right)=m^2 y_1 y_2+m\left(y_1+y_2\right)+1\)
\(=-\dfrac{3}{m^2-4}-\dfrac{2 m}{m^2-4}+1=-\dfrac{4 m^2+4}{m^2-4}=-4-\dfrac{20}{m^2-4}\)
所以 \(\overrightarrow{Q M} \cdot \overrightarrow{Q N}=\left(x_1-t, y_1\right)\left(x_2-t, y_2\right)=\left(x_1-t\right)\left(x_2-t,\right)+y_1 y_2\)
\(=x_1 x_2-t\left(x_1+x_2\right)+y_1 y_2=x_1 x_2-t\left(x_1+x_2\right)+t^2+y_1 y_2\)
\(=-4-\dfrac{20}{m^2-4}+t \cdot \dfrac{8}{m^2-4}-\dfrac{3}{m^2-4}+t^2\)
\(=-4+t^2+\dfrac{8 t-23}{m^2-4}\)为常数,与\(m\)无关,
所以\(8t-23=0\),解得 \(t=\dfrac{23}{8}\),
此时 \(\overrightarrow{Q M} \cdot \overrightarrow{Q N}=\dfrac{273}{64}\).
点拨 这是定点问题,先设元(设定点坐标)再根据已知条件求出其元的值,从而确定定点.
巩固练习
1.双曲线\(E:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)被斜率为\(4\)的直线截得的弦\(AB\)的中点为\((2,1)\),则双曲线\(E\)的离心率为( )
A. \(\sqrt{2}\) \(\qquad \qquad\) B. \(\sqrt{3}\) \(\qquad \qquad\) C.\(2\) \(\qquad \qquad\) D. \(\sqrt{5}\)
2.已知双曲线\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)的渐*线为 \(y=\pm \sqrt{3} x\),过右焦点\(F\)的直线\(l\)与双曲线交于\(A\),\(B\)两点且 \(\overrightarrow{A F}=3 \overrightarrow{F B}\),则直线\(l\)的斜率为( )
A. \(\pm \sqrt{3}\) \(\qquad \qquad\) B. \(\pm \sqrt{15}\) \(\qquad \qquad\) C.\(±1\) \(\qquad \qquad\) D. \(\pm \sqrt{5}\)
3.已知双曲线 \(Γ:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\),\(O\)为坐标原点.
(1)若\(Γ\)为等轴双曲线,且\(Γ\)的右焦点\(F\)到点\(O\)的距离为\(2\),求\(Γ\)的方程;
(2) \(a=\sqrt{2}\), \(b=\sqrt{3}\),设斜率为\(1\)的直线\(l\)交\(Γ\)于\(P\)、\(Q\)两点,且\(OP⊥OQ\),若\(l\)与圆 \(x^2+y^2=r^2 (r>0)\)相切,求\(r\)的值.
4.已知双曲线的方程 \(C:2x^2-y^2=1\).
(1)求点\(P(0,1)\)到双曲线\(C\)上点的距离的最小值;
(2)已知圆 \(M:x^2+y^2=1\)的切线\(l\)(直线\(l\)的斜率存在)与双曲线\(C\)交于\(A\)、\(B\)两点,那么\(∠AOB\)是否为定值?如果是,求出定值;如果不是,请说明理由.
参考答案
- 答案 \(B\)
解析 设\(A(x_1,y_1 )\),\(B(x_2,y_2 )\)代入双曲线方程作差有 \(\dfrac{\left(x_1-x_1\right)\left(x_1+x_2\right)}{a^2}=\dfrac{\left(y_1-y_2\right)\left(y_1+y_2\right)}{b^2}\),
双曲线 \(E:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)被斜率为\(4\)的直线截得的弦\(AB\)的中点为\((2,1)\),
所以\(x_1+x_2=4\),\(y_1+y_2=2\),
有 \(\dfrac{b^2}{a^2}=\dfrac{\left(y_1-y_2\right)\left(y_1+y_2\right)}{\left(x_1-x_2\right)\left(x_1+x_2\right)}=2\),所以 \(\dfrac{c^2}{a^2}=3\), \(e=\sqrt{3}\),
故选:\(B\). - 答案
解析 双曲线\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)的渐*线为 \(y=\pm \sqrt{3} x\),可得 \(b=\sqrt{3} a\),\(c=2a\),
双曲线的方程即为 \(3x^2-y^2=3a^2\),
由 \(\overrightarrow{A F}=3 \overrightarrow{F B}\),可得\(A,F,B\)三点共线,且\(A,B\)均在双曲线的右支上,
设\(A,B\)的纵坐标分别为\(y_1\),\(y_2\),可得\(-y_1=3y_2\),①
可设直线\(l\)的方程为\(x=my+c\),即\(x=my+2a\),
联立双曲线的方程 \(3x^2-y^2=3a^2\),可得 \((3m^2-1) y^2+12amy+9a^2=0\),
可得 \(y_1+y_2=-\dfrac{12 a m}{3 m^2-1}\), \(y_1 y_2=\dfrac{9 a^2}{3 m^2-1}\),②
联立①②可得 \(-3 \cdot \dfrac{36 a^2 m^2}{\left(3 m^2-1\right)^2}=\dfrac{9 a^2}{3 m^2-1}\),
化为\(15m^2=1\),解得 \(m=\pm \dfrac{\sqrt{15}}{15}\),
则直线\(l\)的斜率为 \(\pm \sqrt{15}\).
故选:\(B\). - 答案 (1) \(\dfrac{x^2}{2}-\dfrac{y^2}{2}=1\) (2) \(\sqrt{6}\)
解析 (1)\(Γ\)为等轴双曲线,可得\(a=b\),
由\(Γ\)的右焦点\(F(c,0)\)到点\(O\)的距离为\(2\),可得\(c=2\),即 \(a^2+b^2=4\),
解得 \(a=b=\sqrt{2}\),
则双曲线的方程为 \(\dfrac{x^2}{2}-\dfrac{y^2}{2}=1\);
(2)由题意可得 \(\Gamma: \dfrac{x^2}{2}-\dfrac{y^2}{3}=1,\),设直线\(l:y=x+m\),\(P(x_1,y_1 )\),\(Q(x_2,y_2 )\),
将直线方程代入双曲线方程,并化简得 \(x^2-4mx-(2m^2+6)=0\),
则 \(△=16m^2-4(2m^2+6)>0\),解得 \(m>\sqrt{3}\)或 \(m<-\sqrt{3}\),
且\(x_1+x_2=4m\),\(x_1 x_2=-2m^2-6\),\((*)\)
\(∵OP⊥OQ\),
\(∴x_1 x_2+y_1 y_2=x_1 x_2+(x_1+m)(x_2+m)=2x_1 x_2+m(x_1+x_2)+m^2=0\),
将\((*)\)代入,得\(m^2=12\),
\(\therefore m=\pm 2 \sqrt{3}\),
又直线\(l\)与圆相切,可得 \(r=d=\dfrac{|m|}{\sqrt{2}}=\sqrt{6}\). - 答案 (1) \(\dfrac{\sqrt{30}}{6}\) (2) \(90°\)
解析 (1)设\(Q(a,b)\)为双曲线上的点,则 \(2a^2-b^2=1\),
则 \(|P Q|=\sqrt{a^2+(b-1)^2}=\sqrt{\dfrac{3}{2} b^2-2 b+\dfrac{3}{2}}=\sqrt{\dfrac{3}{2}\left(b-\dfrac{2}{3}\right)^2+\dfrac{5}{6}}\),
当 \(b=\dfrac{2}{3}\)时\(|PQ|\)最小,且为 \(\dfrac{\sqrt{30}}{6}\),
所以点\(P(0,1)\)到双曲线\(C\)上点的距离的最小值为 \(\dfrac{\sqrt{30}}{6}\);
(2)设直线\(l\)的方程为\(y=kx+t\),
由直线\(l\)与圆相切,可得 \(d=\dfrac{|t|}{\sqrt{1+k^2}}=1\),即 \(t^2=1+k^2\),
设\(A(x_1,y_1 )\),\(B(x_2,y_2 )\),联立 \(\left\{\begin{array}{l} y=k x+t \\ 2 x^2-y^2=1 \end{array}\right.\),
可得 \((2-k^2 ) x^2-2ktx-t^2-1=0\),
则 \(2-k^2≠0\), \(x_1+x_2=\dfrac{2 k t}{2-k^2}\),\(x_1 x_2=-\dfrac{t^2+1}{2-k^2}=-\dfrac{2+k^2}{2-k^2}\)
所以 \(y_1 y_2=\left(k x_1+t\right)\left(k x_2+t\right)=k^2 x_1 x_2+k t\left(x_1+x_2\right)+t^2\)
\(=\dfrac{-k^2 t^2-k^2+2 k^2 t^2+2 t^2-k^2 t^2}{2-k^2}=\dfrac{2 t^2-k^2}{2-k^2}=\dfrac{2+k^2}{2-k^2}\),
所以 \(\overrightarrow{O A} \cdot \overrightarrow{O B}=x_1 x_2+y_1 y_2=-\dfrac{2+k^2}{2-k^2}+\dfrac{2+k^2}{2-k^2}=0\),
所以\(∠AOB\)为定值\(90°\).
分层练习
【A组---基础题】
1.直线\(y=kx(k>0)\)与双曲线 \(\dfrac{x^2}{2}-\dfrac{y^2}{6}=1\)没有交点,则\(k\)的取值范围为( )
A. \(\left[\dfrac{\sqrt{3}}{3},+\infty\right)\) \(\qquad \qquad\) B.\((2,+∞)\) \(\qquad \qquad\) C. \([\sqrt{3},+\infty)\) \(\qquad \qquad\) D. \((0, \sqrt{3})\)
2.过双曲线 \(\dfrac{x^2}{3}-y^2=1\)的右焦点\(F\),作倾斜角为\(60°\)的直线\(l\),交双曲线的渐*线于点\(A\)、\(B\),\(O\)为坐标原点,则\(△OAB\)的面积为( )
A. \(\sqrt{3}\) \(\qquad \qquad\) B.\(3\) \(\qquad \qquad\) C. \(\dfrac{3 \sqrt{3}}{2}\) \(\qquad \qquad\) D.\(6\)
3.已知倾斜角为 \(\dfrac{\pi}{4}\)的直线与双曲线 \(C:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)相交于\(A\),\(B\)两点,\(M(4,2)\)是弦\(AB\)的中点,则双曲线的离心率为\(\underline{\quad \quad}\) .
4.已知曲线 \(C:x^2-y^2=1\)及直线\(l:y=kx-1\).且直线\(l\)与双曲线\(C\)有两个不同的交点\(A\),\(B\).
(1)求实数\(k\)的取值范围;
(2)\(O\)是坐标原点,且\(△AOB\)的面积为 \(\sqrt{2}\),求实数k的值.
5.已知双曲线 \(C:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)的焦距为 \(2 \sqrt{5}\),且过点 \(A(2 \sqrt{2},-1)\),直线\(l\)与曲线\(C\)右支相切(切点不为右项点),且\(l\)分别交双曲线\(C\)的两条渐*线与\(M\),\(N\)两点,\(O\)为坐标原点.
(1)求双曲线\(C\)的方程;
(2)求证:\(△MON\)面积为定值,并求出该定值.

6.已知\(F_1 (-2,0)\),\(F_2 (2,0)\),点\(P\)满足\(|PF_1 |-|PF_2 |=2\),记点\(P\)的轨迹为\(E\).
(1)求轨迹\(E\)的方程;
(2)若直线\(l\)过点\(F_2\)且与轨迹\(E\)交于\(P\)、\(Q\)两点.无论直线\(l\)绕点\(F_2\)怎样转动,在\(x\)轴上总存在定点\(M(m,0)\),使\(MP⊥MQ\)恒成立,求实数\(m\)的值.
参考答案
-
答案 \(C\)
解析 双曲线 \(\dfrac{x^2}{2}-\dfrac{y^2}{6}=1\)的渐*线方程为: \(y=\pm \sqrt{3} x\),
根据双曲线的性质可知直线\(y=kx(k>0)\)与双曲线 \(\dfrac{x^2}{2}-\dfrac{y^2}{6}=1\)没有交点,满足 \(k \geq \sqrt{3}\).
故选:\(C\). -
答案 \(C\)
解析 不妨设点\(A\)在第一象限,点\(B\)在第四象限,因为\(∠OFB=60°\),
双曲线 \(\dfrac{x^2}{3}-y^2=1\)的渐*线方程 \(y=\pm \dfrac{\sqrt{3}}{3} x\),
所以\(∠AOF=30°\),所以\(∠FOB=30°\),
所以\(∠OBA=∠OBF=90°\),所以 \(|O B|=|O F| \cos 30^{\circ}=\sqrt{3}\).
又\(∠AOB=60°\),则\(∠OAB=30°\),所以 \(|O A|=2|O B|=2 \sqrt{3}\),所以\(|AB|=3\),
从而\(△OAB\)的面积为: \(\dfrac{1}{2} \cdot|O A||O B| \sin 60^{\circ}=\dfrac{3 \sqrt{3}}{2}\).
故选:\(C\).

-
答案 \(\dfrac{\sqrt{6}}{2}\)
解析 设\(A\)、\(B\)的坐标分别为\((x_1,y_1 )\),\((x_2,y_2 )\),
则 \(\left\{\begin{array}{l} \dfrac{x_1^2}{a^2}-\dfrac{y_1^2}{b^2}=1 \\ \dfrac{x_2^2}{a^2}-\dfrac{y_2^2}{b^2}=1 \end{array}\right.\),两式相减,整理得, \(\dfrac{y_1-y_2}{x_1-x_2}=\dfrac{b^2\left(x_1+x_2\right)}{a^2\left(y_1+y_2\right)}\),
\(∵\)直线\(AB\)的倾斜角为 \(\dfrac{\pi}{4}\),且弦\(AB\)的中点为\(M(4,2)\),
\(\therefore \tan \dfrac{\pi}{4}=\dfrac{b^2 \times 4}{a^2 \times 2}\),得 \(\dfrac{b^2}{a^2}=\dfrac{1}{2}\),
\(∴\)离心率 \(e=\sqrt{\dfrac{c^2}{a^2}}=\sqrt{1+\dfrac{b^2}{a^2}}=\sqrt{1+\dfrac{1}{2}}=\dfrac{\sqrt{6}}{2}\). -
答案 (1) \(\{k \mid-\sqrt{2}<k<\sqrt{2} \text {, 且 } k \neq \pm 1\}\) (2) \(\pm \dfrac{\sqrt{6}}{2}\)
解析 (1)设\(A(x_1,y_1 )\),\(B(x_2,y_2 )\),
联立 \(\left\{\begin{array}{l} y=k x-1 \\ x^2-y^2=1 \end{array}\right.\),整理可得\((1-k^2 ) x^2+2kx-2=0\),
当 \(\left\{\begin{array}{l} 1-k^2 \neq 0 \\ \Delta=4 k^2-4\left(1-k^2\right)(-2)>0 \end{array}\right.\)时,直线\(l\)与双曲线由两个不同的交点,
即 \(\left\{\begin{array}{l} k \neq 1 \text { 且 } k \neq-1 \\ -\sqrt{2}<k<\sqrt{2} \end{array}\right.\),
所以\(k\)的取值范围为 \(\{k \mid-\sqrt{2}<k<\sqrt{2} \text {, 且 } k \neq \pm 1\}\);
(2)由(1)可知 \(x_1+x_2=\dfrac{-2 k}{1-k^2}\), \(x_1 x_2=-\dfrac{2}{1-k^2}\),
所以弦长\(|A B|=\sqrt{1+k^2} \cdot \sqrt{\left(x_1+x_2\right)^2-4 x_1 x_2}=\sqrt{1+k^2} \cdot \sqrt{\dfrac{4 k^2}{\left(1-k^2\right)^2}-4 \cdot \dfrac{-2}{1-k^2}}\)
\(=\sqrt{1+k^2} \cdot \dfrac{\sqrt{8-4 k^2}}{\left|1-k^2\right|}\) ,
原点\(O\)到直线\(AB\)的距离 \(d=\dfrac{1}{\sqrt{1+k^2}}\),
所以 \(S_{\triangle A O B}=\dfrac{1}{2} \cdot|A B| \cdot d=\dfrac{1}{2} \cdot \sqrt{1+k^2} \cdot \dfrac{\sqrt{8-4 k^2}}{\left|1-k^2\right|} \cdot \dfrac{1}{\sqrt{1+k^2}}=\sqrt{\dfrac{2-k^2}{\left(1-k^2\right)^2}}\),
由题意 \(\sqrt{2}=\sqrt{\dfrac{2-k^2}{\left(1-k^2\right)^2}}\),解得: \(k=\pm \dfrac{\sqrt{6}}{2}\)符合题意,
所以实数\(k\)的值为 \(\pm \dfrac{\sqrt{6}}{2}\).

-
答案 (1) \(\dfrac{x^2}{4}-y^2=1\) (2) \(2\)
解析 (1)设双曲线的焦距为\(2c\),由题意可得 \(\left\{\begin{array}{l} 2 c=2 \sqrt{5} \\ c^2=a^2+b^2 \\ \dfrac{8}{a^2}-\dfrac{1}{b^2}=1 \end{array}\right.\),解得 \(a^2=4\),\(b^2=1\)
所以双曲线的方程为 \(\dfrac{x^2}{4}-y^2=1\);
(2)证明:设直线\(l\)的方程:\(y=kx+m\),直线与曲线的右支相切(切点表示右顶点)
则 \(\left\{\begin{array}{l} y=k x+m \\ \dfrac{x^2}{4}-y^2=1 \end{array}\right.\),整理可得: \((4k^2-1) x^2+8kmx+4m^2+4=0\),
\(△=64k^2 m^2-4(4k^2-1)(4m^2+4)=0\),可得 \(4k^2=m^2+1\),①
设直线\(l\)与\(x\)轴交于一点\(D\),则 \(O D=-\dfrac{m}{k}\),
\(S_{\triangle O M N}=S_{\triangle M O D}+S_{\triangle N O D}=\dfrac{1}{2}|O D|\left|y_M-y_N\right|=\dfrac{-m}{2 k}|k|\left|x_M-x_N\right|\),
双曲线的渐*线的方程为 \(y=\pm \dfrac{1}{2} x\),
联立 \(\left\{\begin{array}{l} y=\dfrac{1}{2} x \\ y=k x+m \end{array}\right.\),可得 \(M\left(\dfrac{2 m}{1-2 k}, \dfrac{m}{1-2 k}\right)\),
同理可得 \(N\left(\dfrac{-2 m}{1+2 k}, \dfrac{m}{1+2 k}\right)\),
则 \(S_{\triangle M O N}=\dfrac{-m}{2 k}|k|\left|\dfrac{2 m}{1-2 k}+\dfrac{2 m}{1+2 k}\right|=\dfrac{-m}{2 k}|k|\left|\dfrac{4 m}{1-4 k^2}\right|\),
由①及直线\(l\)与曲线\(C\)右支相切,\(m\)与\(k\)异号,
则 \(S_{\triangle M O N}=2\). -
答案 (1) \(x^2-\dfrac{y^2}{3}=1(x \geq 1)\) (2) \(-1\)
解析 (1)由\(|PF_1 |-|PF_2 |=2<|F_1 F_2 |\)知,点\(P\)的轨迹\(E\)是以\(F_1\)、\(F_2\)为焦点的双曲线右支,
由\(c=2\),\(2a=2\), \(∴b^2=3\),故轨迹\(E\)的方程为 \(x^2-\dfrac{y^2}{3}=1(x \geq 1)\).
(2)当直线\(l\)的斜率存在时,设直线方程为\(y=k(x-2)\),\(P(x_1,y_1 )\),\(Q(x_2,y_2 )\),
与双曲线方程联立消\(y\)得 \((k^2-3) x^2-4k^2 x+4k^2+3=0\),
\(\therefore\left\{\begin{array}{l} k^2-3 \neq 0 \\ \Delta>0 \\ x_1+x_2=\dfrac{4 k^2}{k^2-3}>0 \\ x_1 \cdot x_2=\dfrac{4 k^2+3}{k^2-3}>0 \end{array}\right.\),解得 \(k^2>3\).
\(\because \overrightarrow{M P} \cdot \overrightarrow{M Q}=\left(x_1-m\right)\left(x_2-m\right)+y_1 y_2\)
\(=\left(x_1-m\right)\left(x_2-m\right)+k^2\left(x_1-2\right)\left(x_2-2\right)\)
\(=\left(k^2+1\right) x_1 x_2-\left(2 k^2+m\right)\left(x_1+x_2\right)+m^2+4 k^2\)
\(=\dfrac{\left(k^2+1\right)\left(4 k^2+3\right)}{k^2-3}-\dfrac{4 k^2\left(2 k^2+m\right)}{k^2-3}+m^2+4 k^2\)
\(=\dfrac{3-(4 m+5) k^2}{k^2-3}+m^2\).
\(∵MP⊥MQ\), \(\therefore \overrightarrow{M P} \cdot \overrightarrow{M Q}=0\),
故得\(3(1-m^2 )+k^2 (m2-4m-5)=0\)对任意的 \(k^2>3\)恒成立,
\(\therefore\left\{\begin{array}{l} 1-m^2=0 \\ m^2-4 m-5=0 \end{array}\right.\),解得\(m=-1\).
\(∴\)当\(m=-1\)时,\(MP⊥MQ\).
当直线\(l\)的斜率不存在时,由\(P(2,3)\),\(Q(2,-3)\)及\(M(-1,0)\)知结论也成立,
综上,当\(m=-1\)时,\(MP⊥MQ\).

【B组---提高题】
1.已知\(F_1\),\(F_2\)为双曲线 \(C: x^2-\dfrac{y^2}{b^2}=1(b>0)\)的左、右焦点,过\(F_2\)作垂直于\(x\)轴的垂线,在\(x\)轴上方交双曲线\(C\)于点\(M\),且\(∠MF_1 F_2=30°\).
(1)求双曲线\(C\)的两条渐*线的夹角\(θ\)的正切值;
(2)过点\(F_2\)的直线\(l\)和双曲线\(C\)的右支交于\(A\),\(B\)两点,求\(△AF_1 B\)的面积最小值;
(3)过双曲线\(C\)上任意一点\(Q\)分别作该双曲线两条渐*线的*行线,它们分别交两条渐*线于\(Q_1\),\(Q_2\)两点,求*行四边形\(OQ_1 QQ_2\)的面积.
参考答案
- 答案 (1) \(2 \sqrt{2}\) (2) \(4 \sqrt{3}\) (3) \(\dfrac{\sqrt{2}}{2}\)
解析 (1)双曲线 \(C: x^2-\dfrac{y^2}{b^2}=1(b>0)\)的\(a=1\), \(c=\sqrt{1+b^2}\),
可令\(x=c\),解得 \(y=b \sqrt{c^2-1}=b^2\),设\(M(c,b^2)\),
由\(∠MF_1 F_2=30°\),可得 \(b^2=2 \operatorname{ctan} 30^{\circ}=\dfrac{2 \sqrt{3}}{3} \sqrt{1+b^2}\),解得 \(b=\sqrt{2}\),
则双曲线的方程为 \(x^2-\dfrac{y^2}{2}=1\),
可得双曲线的方程为 \(y=\pm \sqrt{2} x\),
即有 \(\tan \theta=\left|\dfrac{\sqrt{2}+\sqrt{2}}{1-\sqrt{2} \times \sqrt{2}}\right|=2 \sqrt{2}\),
(2)当直线\(AB\)的斜率不存在,可得 \(A(\sqrt{3}, 2), B(\sqrt{3},-2)\),
可得\(△AF_1 B\)的面积为 \(\dfrac{1}{2} \times 2 \sqrt{3} \times 4=4 \sqrt{3}\);
直线\(AB\)的斜率存在,设过点\(F_2\)的直线\(l\)设为 \(y=k(x-\sqrt{3})\),
联立双曲线方程 \(2x^2-y^2=2\),
可得\((2-k^2 ) x^2+2√3 k^2 x-3k^2-2=0\),设\(A(x_1,y_1 )\),\(B(x_2,y_2 )\),
又 \(x_1+x_2=-\dfrac{2 \sqrt{3} k^2}{2-k^2}>0\), \(x_1 x_2=-\dfrac{3 k^2+2}{2-k^2}>0\),可得\(k^2>2\),
可得\(△AF_1 B\)的面积为 \(S=\dfrac{1}{2} \cdot 2 c \cdot\left|y_1-y_2\right|=\sqrt{3} \cdot\left|k\left(x_1-x_2\right)\right|\)
\(=\sqrt{3} \cdot|k| \cdot \sqrt{\left(-\dfrac{2 \sqrt{3} k^2}{2-k^2}\right)^2+4 \cdot \dfrac{3 k^2+2}{2-k^2}}=\sqrt{3}|k| \cdot \dfrac{4 \sqrt{1+k^2}}{k^2-2}\),
设 \(t=k^2-2(t>0)\),可得 \(S=4 \sqrt{3} \cdot \dfrac{\sqrt{(2+t)(3+t)}}{t}=4 \sqrt{3} \cdot \sqrt{1+\dfrac{5}{t}+\dfrac{6}{t^2}}>4 \sqrt{3}\),
综上可得\(△AF_1 B\)的面积的最小值为 \(4 \sqrt{3}\);
(3)设\(Q(m,n)\),可得 \(2m^2-n^2=2\),
双曲线的渐*线方程为 \(y=\pm \sqrt{2} x\),
\(Q\)到直线 \(y= \sqrt{2} x\)的距离为 \(d=\dfrac{|\sqrt{2} m-n|}{\sqrt{3}}\),
由*行于直线 \(y=- \sqrt{2} x\)的直线 \(y=-\sqrt{2}(x-m)+n\),
联立直线 \(y= \sqrt{2} x\),可得 \(Q_2\left(\dfrac{n+\sqrt{2} m}{2 \sqrt{2}}, \dfrac{n+\sqrt{2} m}{2}\right)\),
\(\left|O Q_2\right|=\dfrac{\sqrt{6}}{4}|n+\sqrt{2} m|\),
即有行四边形\(OQ_1 QQ_2\)的面积为
\(d \cdot\left|O Q_2\right|=\dfrac{\sqrt{6}}{4}|n+\sqrt{2} m| \cdot \dfrac{|\sqrt{2} m-n|}{\sqrt{3}}=\dfrac{\sqrt{2}}{4} \cdot\left|2 m^2-n^2\right|=\dfrac{\sqrt{2}}{4} \cdot 2=\dfrac{\sqrt{2}}{2}\).
【C组---拓展题】
1.在*面直角坐标系\(xOy\)中,已知点 \(F_1(-\sqrt{17}, 0)\), \(F_2(\sqrt{17}, 0)\),点\(M\)满足\(|MF_1 |-|MF_2 |=2\).记\(M\)的轨迹为\(C\).
(1)求\(C\)的方程;
(2)设点\(T\)在直线 \(x=\dfrac{1}{2}\)上,过\(T\)的两条直线分别交\(C\)于\(A\),\(B\)两点和\(P\),\(Q\)两点,且\(|TA|\cdot|TB|=|TP|\cdot |TQ|\),求直线\(AB\)的斜率与直线\(PQ\)的斜率之和.
参考答案
- 答案 (1) \(x^2-\dfrac{y^2}{16}=1(x \geq 1)\) (2) \(0\)
解析 (1)由双曲线的定义可知,\(M\)的轨迹\(C\)是双曲线的右支,
设\(C\)的方程为 \(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\),\(x≥1\),
根据题意 \(\left\{\begin{array}{l} c=\sqrt{17} \\ 2 a=2 \\ c^2=a^2+b^2 \end{array}\right.\),解得 \(\left\{\begin{array}{l} a=1 \\ b=4 \\ c=\sqrt{17} \end{array}\right.\),
\(∴C\)的方程为 \(x^2-\dfrac{y^2}{16}=1(x \geq 1)\);
(2)(法一)设 \(T\left(\dfrac{1}{2}, m\right)\),直线\(AB\)的参数方程为 \(\left\{\begin{array}{l} x=\dfrac{1}{2}+t \cos \theta \\ y=m+t \sin \theta \end{array}\right.\),
将其代入\(C\)的方程并整理可得,
\(\left(16 \cos ^2 \theta-\sin ^2 \theta\right) t^2+(16 \cos \theta-2 m \sin \theta) t-\left(m^2+12\right)=0\),
由参数的几何意义可知,\(|TA|=t_1\),\(|TB|=t_2\),则 \(t_1 t_2=\dfrac{m^2+12}{\sin ^2 \theta-16 \cos ^2 \theta}=\dfrac{m^2+12}{1-17 \cos ^2 \theta}\),
设直线\(PQ\)的参数方程为 \(\left\{\begin{array}{l} x=\dfrac{1}{2}+\lambda \cos \beta \\ y=m+\lambda \sin \beta \end{array}\right.\), \(|T P|=\lambda_1,|T Q|=\lambda_2\),
同理可得, \(\lambda_1 \lambda_2=\dfrac{m^2+12}{1-17 \cos ^2 \beta}\),
依题意, \(\dfrac{m^2+12}{1-17 \cos ^2 \theta}=\dfrac{m^2+12}{1-17 \cos ^2 \beta}\),则 \(\cos ^2 \theta=\cos ^2 \beta\),
又\(θ≠β\),故\(cosθ=-cosβ\),则\(cosθ+cosβ=0\),
即直线\(AB\)的斜率与直线\(PQ\)的斜率之和为\(0\).
(法二)设 \(T\left(\dfrac{1}{2}, t\right)\),直线\(AB\)的方程为 \(y=k_1\left(x-\dfrac{1}{2}\right)+t\),
\(A(x_1,y_1 )\),\(B(x_2,y_2 )\),设 \(\dfrac{1}{2}<x_1<x_2\),
将直线\(AB\)方程代入\(C\)的方程化简并整理可得
\(\left(16-k_1^2\right) x^2+\left(k_1^2-2 t k_1\right) x-\dfrac{1}{4} k_1^2+k_1 t-t^2-16=0\),
由韦达定理有, \(x_1+x_2=\dfrac{k_1^2-2 k_1 t}{k_1^2-16}\), \(x_1 x_2=\dfrac{-\dfrac{1}{4} k_1^2+k_1 t-t^2-16}{16-k_1^2}\),
又由 \(A\left(x_1, k_1 x_1-\dfrac{1}{2} k_1+t\right)\), \(T\left(\dfrac{1}{2}, t\right)\)可得 \(\mid A T \mid=\sqrt{1+k_1^2}\left(x_1-\dfrac{1}{2}\right)\),
同理可得 \(|B T|=\sqrt{1+k_1^2}\left(x_2-\dfrac{1}{2}\right)\),
\(\therefore|A T||B T|=\left(1+k_1^2\right)\left(x_1-\dfrac{1}{2}\right)\left(x_2-\dfrac{1}{2}\right)=\dfrac{\left(1+k_1{ }^2\right)\left(t^2+12\right)}{k_1{ }^2-16}\),
设直线\(PQ\)的方程为 \(y=k_2\left(x-\dfrac{1}{2}\right)+t\),\(P(x_3,y_3)\),\(Q(x_4,y_4)\),设 \(\dfrac{1}{2}<x_3<x_4\),
同理可得 \(|P T||Q T|=\dfrac{\left(1+k_2^2\right)\left(t^2+12\right)}{k_2^2-16}\),
又 \(|A T||B T|=|P T||Q T|\),则 \(\dfrac{1+k_1^2}{k_1^2-16}=\dfrac{1+k_2^2}{k_2^2-16}\),化简可得 \(k_1^2=k_2^2\),
又\(k_1≠k_2\),则\(k_1=﹣k_2\),即\(k_1+k_2=0\),即直线\(AB\)的斜率与直线\(PQ\)的斜率之和为\(0\).


 浙公网安备 33010602011771号
浙公网安备 33010602011771号