3.2.1 双曲线及其标准方程

${\color{Red}{欢迎到学科网下载资料学习 }}$  

【基础过关系列】2022-2023学年高二数学上学期同步知识点剖析精品讲义(人教A版2019）
\({\color{Red}{ 跟贵哥学数学，so \quad easy！}}\)

选择性必修第一册同步巩固，难度2颗星！

基础知识

双曲线的定义

平面内与两个定点 \(F_1\)，\(F_2\)的距离之差的绝对值等于常数(小于\(F_1 F_2\))的点的轨迹称为双曲线．这两个定点称为双曲线的焦点，两焦点的距离称为双曲线的焦距．
如图，\(P\)是双曲线上一点，\(|PF_1-PF_2 |=2a<F_1 F_2\).

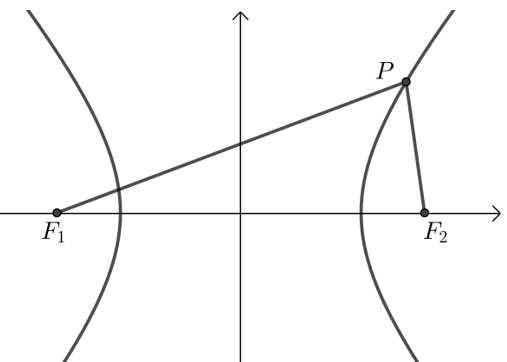
解释
当\(PF_1-PF_2=2a<F_1 F_2\)时，轨迹仅表示双曲线的右支；
当\(PF_2-PF_1=2a<F_1 F_2\)时，轨迹仅表示双曲线的左支；
当\(|PF_1-PF_2 |=2a=F_1 F_2\)时，轨迹是一直线上以\(F_1\)，\(F_2\)为端点向外的两条射线；
当\(|PF_1-PF_2 |=2a>F_1 F_2\)时，轨迹不存在.
 

【例】点\(P\)到两定点\(F_1 (-2,0)\)，\(F_2 (2,0)\)的距离之差为\(2\)，则动点\(P\)的轨迹是什么？
解析 依题意\(PF_1-PF_2=2\)是定值，且小于两定点距离\(F_1 F_2=4\)，
由双曲线定义可知，动点\(P\)的轨迹是双曲线的右支.

 

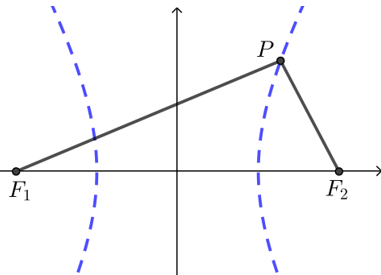
双曲线的标准方程

焦点在\(x\)轴上的双曲线方程为 \(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)；
焦点在\(y\)轴上的双曲线方程为 \(\dfrac{y^2}{a^2}-\dfrac{x^2}{b^2}=1(a>0, \quad b>0)\).
解释
  (1) 双曲线标准方程的证明
双曲线具有对称性，以经过双曲线两焦点的直线为x轴，线段\(F_1 F_2\)的中垂线为\(y\)轴，建立平面直角坐标系，

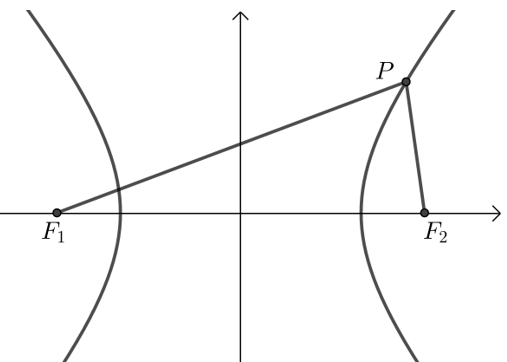
设\(P(x,y)\)是双曲线上任意一点，双曲线的焦距为\(2c(c>0)\)，那么焦点\(F_1 (-c,0)\)，\(F_2 (c,0)\)，根据双曲线定义可得\(|PF_1-PF_2 |=2a\)，则 \(\sqrt{\mid(x+c)^2+y^2}-\sqrt{(x-c)^2+y^2} \mid=2 a\)，
化简得\((c^2-a^2 ) x^2-a^2 y^2=a^2 (c^2-a^2 )\)，
两边同除以\(a^2 (c^2-a^2 )\)得 \(\dfrac{x^2}{a^2}-\dfrac{y^2}{c^2-a^2}=1\)，
即动点\(P\)的轨迹双曲线对应的方程是 \(\dfrac{x^2}{a^2}-\dfrac{y^2}{c^2-a^2}=1\).
由双曲线定义可知\(2c>2a>0\)，即\(c>a>0\)，所以\(c^2-a^2>0\).
令\(b^2=c^2-a^2\)，则我们称 \(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, \quad b>0)\)为双曲线的标准方程.
(焦点在\(y\)轴上的双曲线类似证明)
 

【例】点\(P\)到两定点\(F_1 (-2,0)\)，\(F_2 (2,0)\)的距离之差为\(2\)，求动点\(P\)轨迹方程.
解析 由双曲线的定义可知，动点\(P\)的轨迹是双曲线的右支，且\(2a=2\)，\(c=2\)，
即\(a^2=1\)，\(b^2=c^2-a^2=3\)，则动点\(P\)轨迹方程为 \(x^2-\dfrac{y^2}{3}=1(x>0)\).
(2) 对于方程 \(\dfrac{x^2}{m}+\dfrac{y^2}{n}=1\)，
当\(mn<0\)时，方程表示的轨迹为双曲线；
当\(m>0\),\(n<0\)时，方程表示的轨迹为焦点在\(x\)轴的双曲线；
当\(n>0\),\(m<0\)时，方程表示的轨迹为焦点在\(y\)轴的双曲线；
(由双曲线方程判断焦点的位置与\(a\)的值，我们看分母\(m\),\(n\)的正负)
 

【例】双曲线方程 \(\dfrac{x^2}{9}-\dfrac{y^2}{3}=1\)，其焦点在x轴还是y轴，\(a\)，\(b\)，\(c\)的值又是多少呢？
解析 焦点在\(x\)轴，且\(a=3\)， \(b=\sqrt{3}\)， \(c=2 \sqrt{3}\).
 

焦点三角形

\(F_1\)，\(F_2\)是双曲线 \(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)的焦点，点\(P\)在双曲线上，且与\(F_1\)、\(F_2\)不共线，则三角形\(∆F_1 PF_2\)叫做焦点三角形.

在题目出现焦点三角形\(∆F_1 PF_2\)，可想到双曲线定义\(|PF_1-PF_2 |=2a\)和解三角形的相关知识.
 

基本方法

【题型1】双曲线的定义

【典题1】 若点\(F_1 (-c,0)\)，\(F_2 (c,0)\)(\(c>0\)且为常数)为两个不同的定点，且动点\(M\)满足\(|MF_1 |-|MF_2 |=2a\)(\(2a≥0\)且\(a\)为常数)．求动点\(M\)的轨迹．
解析 若\(2a>2c>0\)，则点\(M\)的轨迹不存在．
若\(2a=2c>0\)，则点\(M\)的轨迹是以点\(F_2\)为端点，且与\(x\)轴正方向同向的射线，方程为\(y=0(x≥c)\)．
若\(0<2a<2c\)，则点\(M\)的轨迹是以\(F_1\),\(F_2\)为焦点的双曲线的右支，其方程为\(\dfrac{x^2}{a^2}-\dfrac{y^2}{c^2-a^2}=1(x≥a)\)．
若\(2a=0\)，则点\(M\)的轨迹是线段\(F_1 F_2\)的垂直平分线，方程为\(x=0\)．
点拨
1.轨迹是满足要求的所有点的集合，注意结合图象理解；
2.轨迹是双曲线，要强调\(|PF_1-PF_2 |\)是定值，且小于\(F_1 F_2\)，绝对符号不能丢.
 

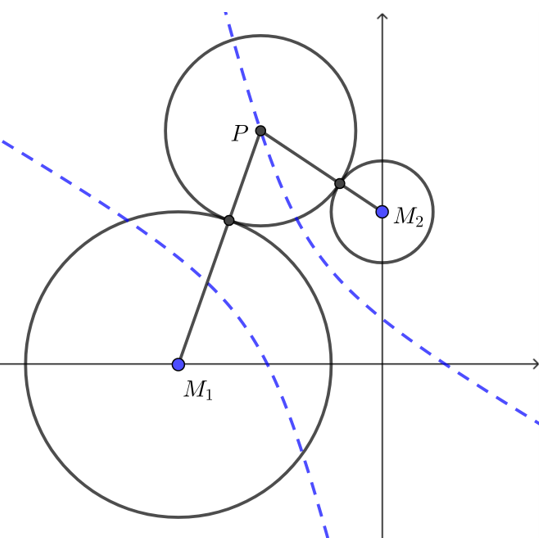
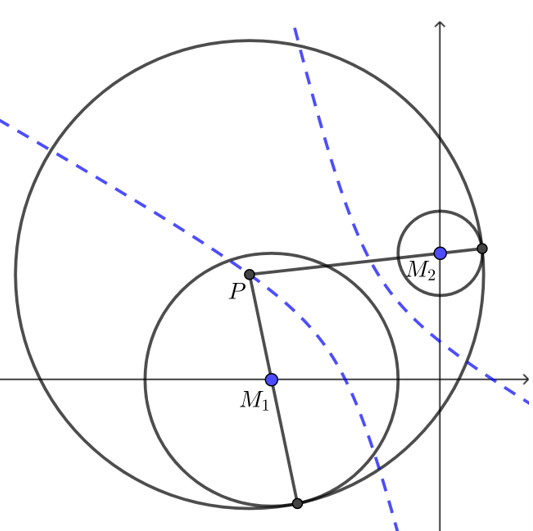
【典题2】已知圆\(M_1:(x+4)^2+y^2=4\)，圆\(M_2:x^2+(y-3)^2=1\)，一动圆\(P\)与这两个圆都外切，试求动圆圆心\(P\)的轨迹方程．
解析 设动圆的圆心为\(P\)，半径为\(r\)，
而圆\(M_1:(x+4)^2+y^2=9\)的圆心为\(O(-4,0)\)，半径为\(3\)；
圆\(M_2:x^2+(y-3)^2=1\)的圆心为\(F(0,3)\)，半径为\(1\)．
依题意得\(\left|P M_1\right|=3+r\),\(\left|P M_2\right|=1+r\)，
则 \(\left|P M_1\right|-\left|P M_2\right|=(3+r)-(1+r)=2<\left|M_1 M_2\right|=5\)，
所以点\(P\)的轨迹是双曲线中靠近焦点\(M_2 (0,3)\)的一支．

 

巩固练习

1.动点\(P\)到点\(M(1,0)\)及点\(N(3,0)\)的距离之差为\(2\)，则点\(P\)的轨迹是(　　)
  A．双曲线 \(\qquad \qquad\) B．双曲线的一支 \(\qquad \qquad\) C．两条射线 \(\qquad \qquad\) D．一条射线
 

2.已知定点\(F_1 (-2,0)\),\(F_2 (2,0)\)在满足下列条件的平面内，动点\(P\)的轨迹为双曲线的是(　　)
 A．\(||PF_1 |-|PF_2∥=3\) \(\qquad \qquad\) B．\(||PF_1 |-|PF_2 ||=4\)
 C．\(||PF_1 |-|PF_2 ||=5\) \(\qquad \qquad\) D．\(|PF_1 |^2-|PF_2 |^2=±4\)
 

3.已知两定点\(F_1 (5,0)\)，\(F_2 (-5,0)\)，曲线\(C\)上的点\(P\)到\(F_1\)，\(F_2\)的距离之差的绝对值是\(8\)，则曲线\(C\)的方程为\(\underline{\quad \quad}\) .
 

4.已知圆\(M_1:(x+3)^2+y^2=4\)，圆\(M_2:x^2+(y-2)^2=1\)，一动圆\(P\)与这两个圆都内切，试求动圆圆心\(P\)的轨迹．
 
 

参考答案

1. 答案 \(D\)
解析 依题意\(|PM|-|PN|=2=|MN|\)，
所以点\(P\)的轨迹不是双曲线，而是一条射线．

2. 答案 \(A\)
解析 根据双曲线定义知\(P\)到\(F_1\)，\(F_2\)的距离之差的绝对值要小于\(|F_1 F_2 |\)，故选\(A\)．

3. 答案 \(\dfrac{x^2}{16}-\dfrac{y^2}{9}=1\)
解析 据双曲线的定义知：\(P\)的轨迹是以\(F_1 (5,0)\)，
\(F_2 (-5,0)\)为焦点，以实轴长为\(8\)的双曲线．
所以\(c=5\)，\(a=4\)，\(b^2=c^2-a^2=9\)，
所以双曲线的方程为： \(\dfrac{x^2}{16}-\dfrac{y^2}{9}=1\).

4. 答案 双曲线中靠近焦点\((-3,0)\)的一支
解析 设动圆的圆心为\(P\)，半径为\(r\)，
而圆\(M_1:(x+3)^2+y^2=4\)的圆心为\(O(-3,0)\)，半径为\(2\)；
圆\(M_2:x^2+(y-2)^2=1\)的圆心为\(F(0,2)\)，半径为\(1\)．
依题意得 \(\left|P M_1\right|=r-2\), \(\left|P M_2\right|=r-1\)，
则 \(\left|P M_2\right|-\left|P M_1\right|=(r-2)-(r-1)=1<\left|M_1 M_2\right|=\sqrt{13}\)，
所以点\(P\)的轨迹是双曲线中靠近焦点\((-3,0)\)的一支．

 

【题型2】双曲线的标准方程

【典题1】 讨论 \(\dfrac{x^2}{25-k}+\dfrac{y^2}{k-9}=1\)表示何种曲线？
解析 由题意可知\(k≠25\)且\(k≠9\)．
当\(k>25\)时，有\(25-k<0\)，\(k-9>0\)，方程表示焦点在\(y\)轴上的双曲线；
当\(k<9\)时，有\(25-k>0\)，\(k-9<0\)，方程表示焦点在\(x\)轴上的双曲线；
当\(9<k<17\)时，\(25-k>0\)，\(k-9>0\)且\(25-k>k-9\)，方程表示焦点在\(x\)轴上的椭圆；
当\(17<k<25\)时，\(25-k>0\)，\(k-9>0\)且\(k-9>25-k\)，方程表示焦点在\(y\)轴上的椭圆；
当\(k=17\)时，\(25-k=k-9=8\)，所给方程表示以原点为圆心，\(2 \sqrt{2}\)为半径的圆．
点拨 对于方程 \(\dfrac{x^2}{m}+\dfrac{y^2}{n}=1\)，判断双曲线的焦点位置和\(a\)值，看分母\(m\),\(n\)的正负；而椭圆看分母\(m\),\(n\)的大小.
 

【典题2】求满足下列条件的双曲线的标准方程：
(1) 已知双曲线的焦点在\(y\)轴上，并且双曲线过点 \((3,-4 \sqrt{2})\)和 \(\left(\dfrac{9}{4}, 5\right)\)；
(2) 已知双曲线的焦点为 \((-\sqrt{5}, 0)\)， \((\sqrt{5}, 0)\)，且过点 \((2 \sqrt{5}, 2)\)；
(3) 与双曲线 \(\dfrac{x^2}{16}-\dfrac{y^2}{4}=1\)有公共焦点，且过点\((3 \sqrt{2}, 2)\)．
解析 (1)设所求双曲线方程为 \(\dfrac{y^2}{a^2}-\dfrac{x^2}{b^2}=1(a>0, b>0)\)，
则 \(\left\{\begin{array}{l} \dfrac{32}{a^2}-\dfrac{9}{b^2}=1 \\ \dfrac{25}{a^2}-\dfrac{81}{16 b^2}=1 \end{array}\right.\)，解得 \(\left\{\begin{array}{l} a^2=16 \\ b^2=9 \end{array}\right.\)，
\(∴\)双曲线的方程为 \(\dfrac{y^2}{16}-\dfrac{x^2}{9}=1\)．
(2) 设所求双曲线方程为 \(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)，
则 \(2 a=\sqrt{(2 \sqrt{5}+\sqrt{5})^2+2^2}-\sqrt{(2 \sqrt{5}-\sqrt{5})^2+2^2}=7-3=4\)，
\(∴a=2\)，又 \(c=\sqrt{5}\)，\(∴b^2=c^2-a^2=1\)，
\(∴\)双曲线的方程为 \(\dfrac{x^2}{4}-y^2=1\)．
(3)方法1 设双曲线方程为 \(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\)，
由题意知 \(c=2 \sqrt{5}\)， \(\therefore a^2+b^2=(2 \sqrt{5})^2=20\)，
\(∵\)双曲线过点 \((3 \sqrt{2}, 2)\)， \(: \dfrac{18}{a^2}-\dfrac{4}{b^2}=1\)，
\(∴a^2=12\),\(b^2=8\)，
故所求双曲线的方程为 \(\dfrac{x^2}{12}-\dfrac{y^2}{8}=1\)．
方法2 设双曲线方程为 \(\dfrac{x^2}{16-k}-\dfrac{y^2}{4+k}=1(-4<k<16)\)，
将点 \((3 \sqrt{2}, 2)\)代入得\(k=4\)，
\(∴\)所求双曲线的方程为 \(\dfrac{x^2}{12}-\dfrac{y^2}{8}=1\)．
点拨
1.求双曲线方程，主要用定义和待定系数法，要注意确定焦点的位置.
2.与双曲线 \(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\)有公共焦点的双曲线的方程为 \(\dfrac{x^2}{a^2-k}-\dfrac{y^2}{b^2+k}=1\left(-b^2<k<a^2\right)\).
 

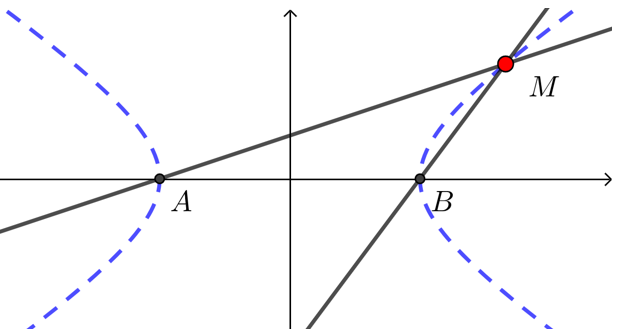
【典题3】点\(A\)，\(B\)的坐标分别是\((-5,0)\)，\((5,0)\)，直线\(AM\)，\(BM\)相交于点\(M\)，且它们斜率之积是 \(\dfrac{4}{9}\)，求点\(M\)的轨迹方程，并判断轨迹的形状.
解析 设点\(M(x,y)\)，
由题意可知 \(k_{A M} \cdot k_{B M}=\dfrac{4}{9}\)，
当\(x≠±5\)时，得 \(\dfrac{y}{x+5} \cdot \dfrac{y}{x-5}=\dfrac{4}{9}\)，化简得 \(\dfrac{x^2}{25}-\dfrac{9 y^2}{100}=1\)，
即点\(M\)的轨迹方程为 \(\dfrac{x^2}{25}-\dfrac{9 y^2}{100}=1(x \neq \pm 5)\)，其轨迹是去掉两个顶点\(A\)，\(B\)的双曲线.

 

巩固练习

1.若\(k∈R\)，则\(k>-3\)是方程 \(\dfrac{x^2}{k-3}+\dfrac{y^2}{k+3}=1\)表示双曲线的 (　　)
  A．充分不必要条件 \(\qquad \qquad\) B．必要不充分条件 \(\qquad \qquad\) C．充要条件 \(\qquad \qquad\) D．既不充分也不必要条件
 

2.若双曲线以椭圆 \(\dfrac{x^2}{16}+\dfrac{y^2}{9}=1\)的两个顶点为焦点，且经过椭圆的两个焦点，则双曲线的标准方程为\(\underline{\quad \quad}\)．
 

3.求与椭圆 \(\dfrac{x^2}{25}+\dfrac{y^2}{5}=1\)有相同焦点，且经过点 \(P(3 \sqrt{2}, 2)\)的双曲线的标准方程．
 

4.已知\(A\),\(B\)两地相距\(800m\)，在\(A\)地听到炮弹爆炸声比在\(B\)地晚\(2s\)，且声速为\(340m/s\)，求炮弹爆炸点的轨迹方程.
 

参考答案

1. 答案 \(B\)
   解析 方程 \(\dfrac{x^2}{k-3}+\dfrac{y^2}{k+3}=1\)表示双曲线，
   可得\((k-3)(k+3)<0\)，解得：\(-3<k<3\)，
   方程 \(\dfrac{x^2}{k-3}+\dfrac{y^2}{k+3}=1\)表示双曲线，可知\(k>-3\)，反之不成立，
   所以\(k∈R\)，则\(k>-3\)是方程 \(\dfrac{x^2}{k-3}+\dfrac{y^2}{k+3}=1\)表示双曲线的必要不充分条件．
   故选：\(B\)．

2. 答案 \(\dfrac{x^2}{7}-\dfrac{y^2}{9}=1\)
   解析 椭圆 \(\dfrac{x^2}{16}+\dfrac{y^2}{9}=1\)的焦点在x轴上，且\(a=4\)，\(b=3\)， \(c=\sqrt{7}\)，
   所以焦点为\((±\sqrt{7},0)\)，顶点为\((±4,0)\)．
   于是双曲线经过点(±√7,0)，焦点为(±4,0)，
   于是 \(a^{\prime}=\sqrt{7}\)， \(c^{\prime}=4\)，所以 \(b^{\prime 2}=9\)，
   所以双曲线的标准方程为 \(\dfrac{x^2}{7}-\dfrac{y^2}{9}=1\)．

3. 答案 \(\dfrac{x^2}{12}-\dfrac{y^2}{8}=1\)
   解析 椭圆 \(\dfrac{x^2}{25}+\dfrac{y^2}{5}=1\)的焦点为 \((\pm 2 \sqrt{5}, 0)\)，
   设所求双曲线方程为 \(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\)，
   由题意知 \(\left\{\begin{array}{l} c^2=a^2+b^2=20 \\ \dfrac{18}{a^2}-\dfrac{4}{b^2}=1 \end{array}\right.\)，即得\(a^2=12\)或\(a^2=30\)(舍)，
   \(∴b^2=c^2-a^2=8\)．
   \(∴\)双曲线标准方程为 \(\dfrac{x^2}{12}-\dfrac{y^2}{8}=1\)．

4. 答案 \(\dfrac{x^2}{115600}-\dfrac{y^2}{44400}=1(x \geqslant 340)\)
   解析 如图，建立平面直角坐标系\(Oxy\)，使\(A\),\(B\)两点在\(x\)轴上，并且原点\(O\)与线段\(AB\)中点重合，
   
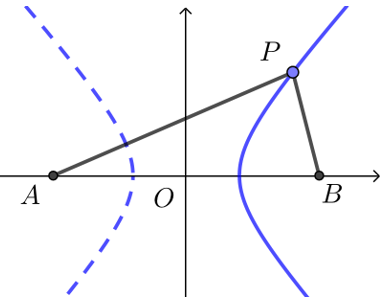
   设炮弹爆炸点\(P\)的坐标为\((x,y)\)，则\(PA-PB=340×2=680\)，
   即\(2a=680\)，\(a=340\)，
   又\(AB=800\)，所以\(2c=800\)，\(c=400\)，\(b^2=c^2-a^2=44400\)，
   因为\(PA-PB=680>0\)，所以点\(P\)的轨迹是双曲线的右支，因此\(x≥340\)，
   所以炮弹爆炸点的轨迹方程为 \(\dfrac{x^2}{115600}-\dfrac{y^2}{44400}=1(x \geqslant 340)\).

【题型3】双曲线的焦点三角形

【典题1】 已知\(F_1\),\(F_2\)是双曲线 \(\dfrac{x^2}{4}-y^2=1\)的两个焦点，\(P\)是双曲线上一点，且\(∠F_1 PF_2=90°\)，则\(△F_1 PF_2\)的面积是\(\underline{\quad \quad}\) ．

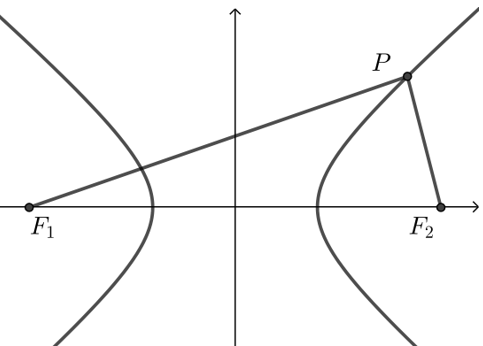
解析 方法1 设\(|PF_1 |=d_1\)，\(|PF_2 |=d_2\)，
由双曲线的定义可知\(|d_1-d_2 |=4\)．又\(∠F_1 PF_2=90°\)，
于是有\(d_1^2+d_2^2=|F_1 F_2 |^2=20\)，
因此， \(S_{\Delta F_1 P F_2}=\dfrac{1}{2} d_1 d_2=\dfrac{1}{4}\left(d_1+d_2-\left|d_1-d_2\right|^2\right)=1\)．
方法2 由 \(\dfrac{x^2}{4}-y^2=1\)，知 \(\left|F_1 F_2\right|=2 \sqrt{5}\)．
设\(P\)点的纵坐标为\(y_P\)，由于\(∠F_1 PF_2=90^∘\)，
则\(P\)在以\(|F_1 F_2 |\)为直径的圆上，即在\(x^2+y^2=5\)上．
由 \(\left\{\begin{array}{l} x^2+y^2=5 \\ x^2-4 y^2=4 \end{array}\right.\)消去\(x\)得 \(\left|y_P\right|=\dfrac{\sqrt{5}}{5}\)，
故\(△F_1 PF_2\)的面积 \(S=\dfrac{1}{2}\left|F_1 F_2\right| \cdot\left|y_P\right|=1\)．
点拨
1.在题目出现焦点三角形\(∆F_1 PF_2\)，可想到双曲线定义\(|PF_1-PF_2 |=2a\)和解三角形的相关知识；
2.双曲线中的焦点三角形面积为 \(S=\dfrac{b^2}{\tan \frac{\angle F_1 P F_2}{2}}\)，本题使用公式得 \(S=\dfrac{b^2}{\tan \frac{\angle F_1 P F_2}{2}}=\dfrac{1}{\tan 45^{\circ}}=1\).
 

【典题2】已知双曲线 \(\dfrac{x^2}{4}-\dfrac{y^2}{b^2}=1(b>0)\)的左右焦点分别为\(F_1\)，\(F_2\)，过点\(F_2\)的直线交双曲线右支于\(A\)、\(B\)两点，若\(△ABF_1\)是等腰三角形，且\(∠A=120°\)，则\(△ABF_1\)的周长为\(\underline{\quad \quad}\) ．

解析 由双曲线\(\dfrac{x^2}{4}-\dfrac{y^2}{b^2}=1(b>0)\)，可得\(a=2\)，
如图所示，设\(|AF_2 |=m\)，\(|BF_2 |=n\)，
可得\(|AF_1 |=4+m\)，\(|BF_1 |=4+n\)，
\(∴4+m=m+n\)．解得\(n=4\)．
作\(AD⊥BF_1\)，垂足为\(D\)，\(D\)为线段\(BF_1\)的中点，\(∠F_1 AD=60°\)．
\(\therefore\left|D F_1\right|=\dfrac{\sqrt{3}}{2}(4+m)\)，
\(\therefore \dfrac{\sqrt{3}}{2}(4+m) \times 2=4+n\)，即 \(\sqrt{3}(4+m)=4+n\)．
又\(n=4\)，代入解得： \(m=\dfrac{8 \sqrt{3}}{3}-4\)．
\(∴△ABF_1\)的周长 \(=4+m+m+n+4+n=8+2(m+n)=8+\dfrac{16 \sqrt{3}}{3}\)．
 

巩固练习

1.双曲线 \(\dfrac{x^2}{25}-\dfrac{y^2}{9}=1\)上的点到一个焦点的距离为\(12\)，则到另一个焦点的距离为(　 )
  A．\(22\)或\(2\) \(\qquad \qquad\) B．\(7\) \(\qquad \qquad\) C．\(22\) \(\qquad \qquad\) D．\(2\)
 

2.已知\(F_1\)、\(F_2\)为双曲线 \(C: \dfrac{x^2}{3}-y^2=1\)的左、右焦点，点\(P\)在\(C\)上，\(∠F_1 PF_2=60°\)，则\(△PF_1 F_2\)的面积为(　　)
 A．\(\sqrt{3}\) \(\qquad \qquad\) B．\(\dfrac{\sqrt{3}}{3}\) \(\qquad \qquad\) C．\(\dfrac{\sqrt{3}}{2}\) \(\qquad \qquad\) D．\(2 \sqrt{3}\)
 

3.设点\(F_1\)，\(F_2\)分别为双曲线 \(C: \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)的左、右焦点，点\(A\)、\(B\)分别在双曲线\(C\)的左、右支上，若 \(\overrightarrow{F_1 B}=6 F_1 A\)， \(\overrightarrow{A F}_2^2=\overrightarrow{A B} \cdot \overrightarrow{A F_2}\)，且 \(\left|\overrightarrow{A F_2}\right|<\left|\overrightarrow{B F_2}\right|\)，则 \(\dfrac{b}{a}=\) \(\underline{\quad \quad}\) .
 

参考答案

1. 答案 \(A\)
解析 \(a^2=25\)，所以\(a=5\)，\(2a=10\)，
由双曲线的定义知双曲线上的点到两焦点距离差的绝对值为\(10\)，
故到另一焦点的距离为\(22\)或\(2\)．

2. 答案 \(A\)
解析 双曲线 \(C: \dfrac{x^2}{3}-y^2=1\)，可得 \(a=\sqrt{3}\)，\(b=1\)，则\(c=2\)，
设\(|PF_1 |=m\)，\(|PF-2 |=n\)，
由双曲线的定义可得： \(|m-n|=2 a=2 \sqrt{3}\)，则有\(m^2+n^2－2mn=12\)，①
又由\(∠F_1 PF_2=60^∘\)，则有\(m^2+n^2-2mncos⁡60^∘=4c^2=16\)，②
联立①②解可得\(mn=4\)，
则\(△PF_1 F_2\)的面积 \(S=\dfrac{1}{2} m n \sin 60^{\circ}=\sqrt{3}\)；
故选：\(A\)．

3. 答案 \(\dfrac{2 \sqrt{10}}{5}\)
解析 \(\because \overrightarrow{F_1 B}=6 \overrightarrow{F_1 A}\)，\(∴F_1,A,B\)共线，且 \(|\overrightarrow{A B}|=5\left|\overrightarrow{A F_1}\right|\)，
\(\because \overrightarrow{A F}_2^2=\overrightarrow{A B} \cdot \overrightarrow{A F_2}=\left(\overrightarrow{A F_2}+\overrightarrow{F_2 B}\right) \cdot \overrightarrow{A F_2}=\overrightarrow{A F}_2^2+\overrightarrow{F_2 B} \cdot \overrightarrow{A F_2}\)，
\(\therefore \overrightarrow{F_2 B} \cdot \overrightarrow{A F_2}=0\)，则 \(\overrightarrow{F_2} B \perp \overrightarrow{A F_2}\)．故有 \(\left|\overrightarrow{A F_2}\right|^2+\left|\overrightarrow{B F_2}\right|^2=|\overrightarrow{A B}|^2\)，
设 \(\left|\overrightarrow{A F_1}\right|=m\)，则 \(|\overrightarrow{A B}|=5 m,\left|\overrightarrow{B F_1}\right|=6 m\)，
由双曲线的定义可得 \(\left|\overrightarrow{A F_2}\right|-m=2 a\), \(6 m-\left|\overrightarrow{B F_2}\right|=2 a\)，且有 \(\left|\overrightarrow{A F}_2\right|^2+\left|\overrightarrow{B F}_2\right|^2=25 m^2\)，
解得\(m=a\)或 \(m=\dfrac{2}{3} a\)．
若\(m=a\)，则 \(| \overrightarrow{A F}_2|=3 a<| \overrightarrow{B F}_2 \mid=4 a\)，舍去；
若 \(m=\dfrac{2}{3} a\)，则 \(\left|\overrightarrow{A F}_2\right|=\dfrac{8}{3} a\), \(\left|\overrightarrow{B F}_2\right|=2 a\), \(\left|\overrightarrow{B F}_1\right|=4 a\)，\(|\overrightarrow{A B}|=\dfrac{10}{3} a\).
\(\cos \angle A B F_2=\dfrac{\left|\overrightarrow{A F_2}\right|}{|\overrightarrow{A B}|}=\dfrac{2 a}{\dfrac{10}{3} a}=\dfrac{3}{5}\)．
在\(△F_1 BF_2\)中， \(4 c^2=4 a^2+16 a^2-2 \times 2 a \times 4 a \times \dfrac{3}{5}\)，得到 \(\dfrac{c^2}{a^2}=\dfrac{13}{5}\)，
即 \(c^2=\dfrac{13}{5} a^2\)，所以 \(b^2=c^2-a^2=\dfrac{13}{5} a^2-a^2=\dfrac{8}{5} a^2\)．
所以 \(\dfrac{b}{a}=\sqrt{\dfrac{\dfrac{8}{5} a^2}{a^2}}=\dfrac{2 \sqrt{10}}{5}\).

 

分层练习

【A组---基础题】

1.已知两定点\(F_1 (-5,0)\),\(F_2 (5,0)\)，动点\(P\)满足\(|PF_1 |-|PF_2 |=2a\)，则当\(a=3\)和\(5\)时，\(P\)点的轨迹分别是(　　)．
  A．双曲线和一条直线 \(\qquad \qquad\) B．双曲线和一条射线 \(\qquad \qquad\) C．双曲线的一支和一条射线\(\qquad \qquad\) D．双曲线的一支和一条直线
 

2.已知方程 \(\dfrac{x^2}{1+k}-\dfrac{y^2}{1-k}=1\)表示双曲线，则\(k\)的取值范围是(　　)．
 A．\(-1<k<1\) \(\qquad \qquad\) B．\(k>0\) \(\qquad \qquad\) C．\(k≥0\) \(\qquad \qquad\) D．\(k>1\)或\(k<-1\)
 

3.设双曲线 \(C: \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)，的左、右焦点分别为\(F_1\) 、\(F_2\)，离心率为 \(\sqrt{3}\)．\(P\)是\(C\)上一点，且\(∠F_1 PF_2=60°\)，若\(△F_1 PF_2\)的面积为 \(4 \sqrt{3}\)，则\(a=\)(　　)
 A．\(1\) \(\qquad \qquad\) B．\(2\) \(\qquad \qquad\) C．\(4\) \(\qquad \qquad\) D． \(\sqrt{2}\)
 

4.设双曲线 \(C: \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>b>0)\)的左、右焦点分别为\(F_1\) 、\(F_2\)，过\(F_1\)的直线\(l\)与双曲线左右两支交于\(M\)，\(N\)两点，以\(MN\)为直径的圆过\(F_2\)，且 \(\overrightarrow{M N}^2=2 \overrightarrow{M F_2} \cdot \overrightarrow{M N}\)，则 \(\dfrac{c}{a}=\) (　　)
 A． \(\sqrt{2}\) \(\qquad \qquad\) B． \(\sqrt{3}\) \(\qquad \qquad\) C．\(2\) \(\qquad \qquad\) D． \(\sqrt{5}\)
 

5.一动圆\(P\)过定点\(M(－4,0)\)，且与已知圆\(N：(x-4)^2+y^2=16\)相切，则动圆圆心\(P\)的轨迹方程是\(\underline{\quad \quad}\) .
 

6.设椭圆\(C_1\)的离心率为 \(\dfrac{5}{13}\)，焦点在\(x\)轴上且长轴长为\(26\)，若曲线\(C_2\)上的点到椭圆\(C_1\)的两焦点的距离差的绝对值等于\(8\)，则曲线\(C_2\)的标准方程为\(\underline{\quad \quad}\) .
 

7.如图所示，已知双曲线 \(C: \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)的右焦点为\(F\)，双曲线\(C\)的右支上一点\(A\)，它关于原点\(O\)的对称点为\(B\)，满足\(∠AFB=120^°\)，且\(|BF|=2|AF|\)，则 \(\dfrac{c}{a}=\) .

 

8.在下列条件下求双曲线标准方程．
(1) 经过两点 \((4, \sqrt{3})\)、 \(\left(3, \dfrac{\sqrt{5}}{2}\right)\)；
(2) \(a=2 \sqrt{5}\)，经过点\((2,-5)\)，焦点在\(y\)轴上．
 
 

. 参考答案

1. 答案 \(B\)
解析 当\(a=3\)时，\(|PF_1 |-|PF_2 |=6<|F_1 F_2 |\)，
所以\(P\)点轨迹是双曲线的一支；
当\(a=5\)时，\(|PF_1 |-|PF_2 |=10=|F_1 F_2 |\)，
所以\(P\)点轨迹是以\(F_2\)为起点的一条射线．

2. 答案 \(A\)
解析 方程 \(\dfrac{x^2}{1+k}-\dfrac{y^2}{1-k}=1\)表示双曲线，则\((1+k)(1-k)>0\)，
\(∴(k+1)(k-1)<0\)，\(∴-1<k<1\)．

3. 答案 \(D\)
解析 根据题意，几何关系如图所示．设\(|PF_2 |=m\)，\(|PF_1 |=n\)，
若\(△F_1 PF_2\)的面积为 \(4 \sqrt{3}\)，
可得\(n-m=2a\)，\(4c^2=m^2+n^2-2mncos60°\)， \(\dfrac{1}{2} m n \sin 60^{\circ}=4 \sqrt{3}\)，
\(∴4c^2=4a^2+2mn-mn=4a^2+mn=4a^2+16\)，
离心率为 \(\sqrt{3}\)．可得 \(\dfrac{c}{a}=\sqrt{3}\)，代入上式，可得\(a=\sqrt{2}\)．
故选：\(D\)．

4. 答案 \(B\)
解析 由\(MN\)为直径的圆过\(F_2\)，可得\(MF_2⊥NF_2\)，
由 \(\overrightarrow{M N}{ }^2=2 \overrightarrow{M F_2} \cdot \overrightarrow{M N}\)，得 \(|\overrightarrow{M N}|^2=2\left|\overrightarrow{M F_2}\right| \cdot|\overrightarrow{M N}| \cdot \cos \angle F_2 M N\)，
即 \(\dfrac{1}{2}|\overrightarrow{M N}|=\left|\overrightarrow{M F_2}\right| \cdot \cos \angle F_2 M N\)，可知\(F_2\)在线段\(MN\)上的投影为\(MN\)的中点，
则\(|MF_2 |=|NF_2 |\)，
设\(|MF_2 |=|NF_2 |=m\)，则 \(|M N|=\sqrt{2} m\)，
由\(|MF_2 |－|MF_1 |=2a\)，\(|NF_2 |－|NF_1 |=2a\)，两式相减可得\(|NF_1 |－|MF_1 |=|MN|=4a\)，
即有 \(m=2 \sqrt{2} a\)，
设\(H\)为\(MN\)的中点，在直角三角形\(HF_1 F_2\)中，
可得 \(4c^2=4 a^2+(2 a+2 \sqrt{2} a-2 a)^2\)，化为\(c^2=3a^2\)，
即 \(\dfrac{c}{a}=\sqrt{3}\)，
故选：\(B\)．

5. 答案 \(\dfrac{x^2}{4}-\dfrac{y^2}{12}=1\)
解析 动圆圆心为\(P\)，半径为\(r\)，已知圆圆心为\(N\)，半径为\(4\)
由题意知：\(PM=r\)，PN=r+4，
所以\(|PN|-PM|=4\)，
即动点\(P\)到两定点的距离之差为常数\(4\)，
\(P\)在以\(M\)、\(C\)为焦点的双曲线上，且\(2a=4\)，\(2c=8\)，
\(\therefore b=2 \sqrt{3}\)，
\(∴\)动圆圆心\(M\)的轨迹方程为： \(\dfrac{x^2}{4}-\dfrac{y^2}{12}=1\)．

6. 答案 \(\dfrac{x^2}{16}-\dfrac{y^2}{9}=1\)
解析 在椭圆\(C_1\)中，由 \(\left\{\begin{array}{l} 2 a=26 \\ \dfrac{c}{a}=\dfrac{5}{13} \end{array}\right.\)得 \(\left\{\begin{array}{l} a=13 \\ c=5 \end{array}\right.\)，
椭圆\(C_1\)的焦点\(F_1 (-5,0)\),\(F_2 (5,0)\)，曲线\(C_2\)是以\(F_1\)，\(F_2\)为焦点，实轴长为\(8\)的双曲线，
故\(C_2\)的标准方程为 \(\dfrac{x^2}{16}-\dfrac{y^2}{9}=1\)．

7. 答案 \(\sqrt{3}\)
解析 连接\(AF'\)，\(BF'\)，由条件可得\(|BF|-|AF|=|AF'|-|AF|=|AF|=2a\)，
则\(|AF|=2a\)，\(|BF|=4a\)，\(∠F'BF=60°\)，
所以\(F'F^2=AF^2+BF^2-2AF⋅BFcos60°\)，可得 \(4 c^2=4 a^2+16 a^2-16 a^2 \times \dfrac{1}{2}\)，
即\(4c^2=12a^2\)，
所以双曲线的离心率为 \(\dfrac{c}{a}=\sqrt{3}\)．

8. 答案 (1) \(\dfrac{x^2}{4}-y^2=1\) (2) \(\dfrac{y^2}{20}-\dfrac{x^2}{16}=1\)
解析 (1) 由题意，设双曲线方程为\(mx^2+ny^2=1\)，代入点 \((4, \sqrt{3})\)、 \(\left(3, \dfrac{\sqrt{5}}{2}\right)\)，
得 \(\left\{\begin{array}{l} 16 m+3 n=1 \\ 9 m+\dfrac{5}{4} n=1 \end{array}\right.\)，解得 \(m=\dfrac{1}{4}\),\(n=-1\)．
\(∴\)双曲线的标准方程为 \(\dfrac{x^2}{4}-y^2=1\)；
(2)根据题意， \(a=2 \sqrt{5}\)，其焦点在\(y\)轴上，
设双曲线的标准方程为： \(\dfrac{y^2}{20}-\dfrac{x^2}{b^2}=1\)，
又由双曲线经过点\((2,-5)\)，则 \(\dfrac{25}{20}-\dfrac{4}{b^2}=1\)，解可得\(b^2=16\)，
则双曲线的标准方程为： \(\dfrac{y^2}{20}-\dfrac{x^2}{16}=1\)．
 

【B组---提高题】

1.已知双曲线 \(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\)，\(P\)为双曲线上除\(x\)轴上之外的一点且\(∠F_1 PF_2=θ\)，求\(△PF_1 F_2\)的面积．
 
 

2.已知双曲线 \(\dfrac{x^2}{4}-\dfrac{y^2}{3}=1\)的左、右焦点分别为\(F_1\) 、\(F_2\)，\(O\)为双曲线的中心，\(P\)是双曲线右支上的点，\(△PF_1 F_2\)的内切圆的圆心为\(I\)，且圆\(I\)与\(x\)轴相切于点\(A\)，过\(F_2\)作直线\(PI\)的垂线，垂足为\(B\)，则 \(\dfrac{|O B|}{|O A|}=\) \(\underline{\quad \quad}\) .
 
 

参考答案

1. 答案 \(\dfrac{b^2}{\tan \dfrac{\angle F_1 P F_2}{2}}\)
解析 由面积公式知 \(S_{\triangle P F_1 F_2}=\dfrac{1}{2}\left|P F_1\right| \cdot\left|P F_2\right| \cdot \sin \angle F_1 P F_2\)，
首 先用余弦定理求出\(|PF_1 |⋅|PF_2 |\)的值，
因为 \(\cos \angle F_1 P F_2=\dfrac{\left|P F_1\right|^2+\left|P F_2\right|^2-\left|F_1 F_2\right|^2}{2\left|P F_1\right| \cdot\left|P F_2\right|}=\dfrac{\left(\left|P F_1\right|-\left|P F_2\right|\right)^2-\left|F_1 F_2\right|^2+2\left|P F_1\right| \cdot\left|P F_2\right|}{2\left|P F_1\right| \cdot\left|P F_2\right|}\)
\(=\dfrac{4 a^2-4 c^2+2\left|P F_1\right| \cdot\left|P F_2\right|}{2\left|P F_1\right| \cdot\left|P F_2\right|}=\dfrac{-4 b^2+2\left|P F_1\right| \cdot\left|P F_2\right|}{2\left|P F_1\right| \cdot\left|P F_2\right|}=\dfrac{-2 b^2}{\left|P F_1\right| \cdot\left|P F_2\right|}+1\)．
\(\therefore\left|P F_1\right| \cdot\left|P F_2\right|=\dfrac{2 b^2}{1-\cos \angle F_1 P F_2}\)，
从而得 \(S_{\triangle P F_1 F_2}=\dfrac{b^2}{\tan \dfrac{\angle F_1 P F_2}{2}}\)．

2. 答案 \(1\)
解析 根据题意得 \(F_1(-\sqrt{7}, 0)\)、 \(F_2(\sqrt{7}, 0)\)，
设\(△PF_1 F_2\)的内切圆分别与\(PF_1\) 、\(PF_2\)切于点\(A_1\) 、\(B_1\)，与\(F_1 F_2\)切于点\(A\)，
则\(|PA_1 |=|PB_1 |\)，\(|F_1 A_1 |=|F_1 A|\)，\(|F_2 B_1 |=|F_2 A|\)，
又点\(P\)在双曲线右支上，
\(∴|PF_1 |－|PF_2 |=4\)，故\(|F_1 A|－|F_2 A|=4\)，而 \(\left|F_1 A\right|+\left|F_2 A\right|=2 \sqrt{7}\)，
设\(A\)点坐标为\((x,0)\)，
则由\(|F_1 A|-|F_2 A|=4\)可得 \((x+\sqrt{7})-(\sqrt{7}-x)=4\)，解得\(x=2\)，
故\(|OA|=2\)，
则\(△PF_1 F_2\)的内切圆的圆心在直线\(x=3\)上，
延长\(F_2 B\)交\(PF_1\)于\(C\)，在三角形\(PCF_2\)中，
由题意得，三角形\(PCF_2\)是一个等腰三角形，\(PC=PF_2\)，
\(∴\)在三角形\(F_1 CF_2\)中，有 \(|O B|=\dfrac{1}{2}\left|C F_1\right|=\dfrac{1}{2}\left(\left|P F_1\right|-|P C|\right)=\dfrac{1}{2}\left(\left|P F_1\right|-\left|P F_2\right|\right)=2\)，
\(\therefore \dfrac{|O B|}{|O A|}=1\)．

 

【C组---拓展题】

1.点\(P\)到图形\(C\)上每一个点的距离的最小值称为点\(P\)到图形\(C\)的距离，那么平面内到定圆\(C\)的距离与到定点\(A\)的距离相等的点的轨迹不可能是（　　）
 A．圆 \(\qquad \qquad\) B．椭圆 \(\qquad \qquad\) C．双曲线的一支 \(\qquad \qquad\) D．直线
 

2.(多选)已知\(F_1\)、\(F_2\)分别为双曲线 \(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)的左右焦点，且 \(\left|F_1 F_2\right|=\dfrac{2 b^2}{a}\)，点\(P\)为双曲线右支上一点，\(I\)为\(△PF_1 F_2\)的内心，过原点\(O\)作\(PI\)的平行线交\(PF_1\)于\(K\)，若 \(S_{\triangle I P F_1}=S_{\triangle I P F_2}+\lambda S_{\triangle I F_1 F_2}\)成立，则下列结论正确的有(　　)
A． \(\lambda=\dfrac{\sqrt{5}-1}{2}\) B． \(\lambda=\dfrac{\sqrt{5}+1}{2}\) C．点\(I\)的横坐标为\(a\) D．\(PK=a\)
 

参考答案

1. 答案 \(D\)
解析 排除法：设动点为\(Q\)，

(1)当点\(A\)在圆内不与圆心\(C\)重合，连接\(CQ\)并延长，交于圆上一点\(B\)，由题意知\(QB=QA\)，
又\(QB+QC=R\)，所以\(QA+QC=R\)，即\(Q\)的轨迹为一椭圆；如图．
(2)如果是点\(A\)在圆\(C\)外，由\(QC-R=QA\)，得\(QC-QA=R\)，为一定值，即\(Q\)的轨迹为双曲线的一支；
(3)当点\(A\)与圆心\(C\)重合，要使\(QB=QA\)，则\(Q\)必然在与圆\(C\)的同心圆，即\(Q\)的轨迹为一圆；
则本题选\(D\)．

2. 答案 \(ACD\)
解析 \(\because\left|F_1 F_2\right|=\dfrac{2 b^2}{a}\)，\(\therefore 2 c=\dfrac{2 b^2}{a}=\dfrac{2 c^2-2 a^2}{a}\)，整理得\(e^2-e-1=0\)，

\(∵e>1\)， \(\therefore e=\dfrac{1+\sqrt{5}}{2}\)．
设\(△PF_1 F_2\)的内切圆半径为\(r\)，
由双曲线的定义得\(|PF_1 |-|PF_2 |=2a\)，\(|F_1 F_2 |=2c\)，
\(S_{\triangle I P F_1}=\dfrac{1}{2}\left|P F_1\right| \cdot r\)， \(S_{\triangle I P F_2}=\dfrac{1}{2}\left|P F_2\right| \cdot r\)， \(S_{\triangle I F_1 F_2}=\dfrac{1}{2} \cdot 2 c \cdot r=c r\)，
\(\because S_{\triangle I P F_1}=S_{\triangle I P F_2}+\lambda S_{\triangle I F_1 F_2}\)， \(\therefore \dfrac{1}{2}\left|P F_1\right| \cdot r=\dfrac{1}{2}\left|P F_2\right| \cdot r+\lambda c r\)，
故 \(\lambda=\dfrac{\left|P F_1\right|-\left|P F_2\right|}{2 c}=\dfrac{a}{c}=\dfrac{1}{\dfrac{1+\sqrt{5}}{2}}=\dfrac{\sqrt{5}-1}{2}\)，所以\(A\)正确，\(B\)错误．
设内切圆与\(PF_1\) 、\(PF_2\) 、\(F_1 F_2\)的切点分别为\(M\)，\(N\)，\(T\)，
可得\(|PM|=|PN|\)．\(|F_1 M|=|F_1 T|\)，\(|F_2 N|=|F_2 T|\)．
由\(|PF_1 |-|PF_2 |=|F_1 M|-|F_2 N|=|F_1 T|-|F_2 T|=2a\)，\(|F_1 F_2 |=|F_1 T|+|F_2 T|=2c\)，
可得\(|F_2 T|=c-a\)，可得\(T\)的坐标为\((a,0)\)，即I的横坐标为\(a\)，故\(C\)正确；
设\(PI\)延长线与\(F_1 F_2\)交于\(H\)，可得\(\dfrac{\left|P F_2\right|}{\left|P F_1\right|}=\dfrac{\left|F_2 H\right|}{\left|F_1 H\right|}\)，由\(|PF_1 |－|PF_2 |=2a\)，
可得 \(\dfrac{2 a}{\left|P F_1\right|}=\dfrac{2|O H|}{\left|F_1 H\right|}\)，①
由三角形的相似的性质可得 \(\dfrac{|P K|}{|O H|}=\dfrac{\left|P F_1\right|}{\left|H F_1\right|}\)，②
由①②可得\(|PK|=a\)．故\(D\)正确．
故选：\(ACD\)．