4.5.3 函数模型的应用
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
【基础过关系列】2022-2023学年高一数学上学期同步知识点剖析精品讲义(人教A版2019)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第一册同步巩固,难度2颗星!
基础知识
各种函数的增速
1 一次函数的增长速度
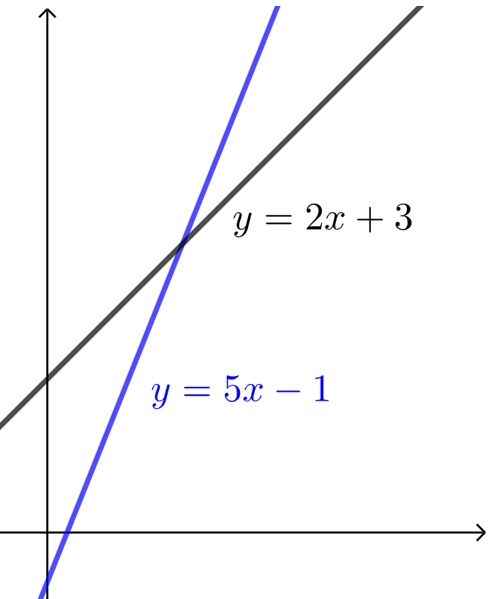
一次函数\(y=kx+b(k>0)\)在区间\((0,+∞)\)上是增函数,其增长的速度不变,\(k\)越大,其增长得越快.
当\(k<0\)时,\(|k|\)越大,其增长得越快.
如 \(y=5x-1\)比\(y=2x+3\)增长得快.
2 幂函数的增长速度
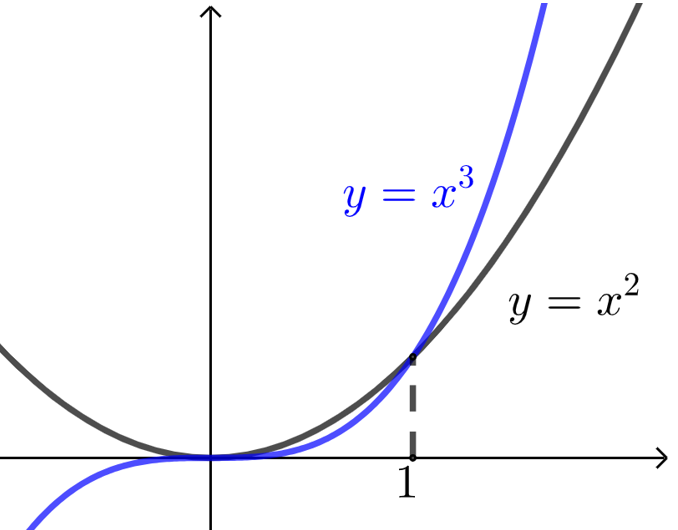
幂函数\(y=x^n (n>0)\)在区间\((0, +∞)\)上是增函数,其增长速度较快,指数\(n\)越大,增长速度越快.
如 \(y=x^3\)比\(y=x^2\)的增长速度更快.当\(0<x<1\)时, \(y=x^3\)的函数值比 \(y=x^2\)小;
当\(x>1\)时,\(y=x^3\)的函数值比 \(y=x^2\)大,并且越来越大.
3 对数函数的增长速度
对数函数\(y=log_ax(a>1)\)在区间\((0,+∞)\)上是增函数,其增长的速度较慢,
随着\(x\)的增大,\(y=log_ax\)的图象类似于与\(x\)轴“平行”一样.
其底数\(a\)越小,增长的速度越快.
如 \(y=log_2x\)比\(y=log_4x\)的增长速度更快.当\(0<x<1\)时,\(y=log_4x\)的函数值比\(y=log_2x\)大;
当\(x>1\)时,\(y=log_4x\)的函数值比\(y=log_2x\)小,并且越来越小.
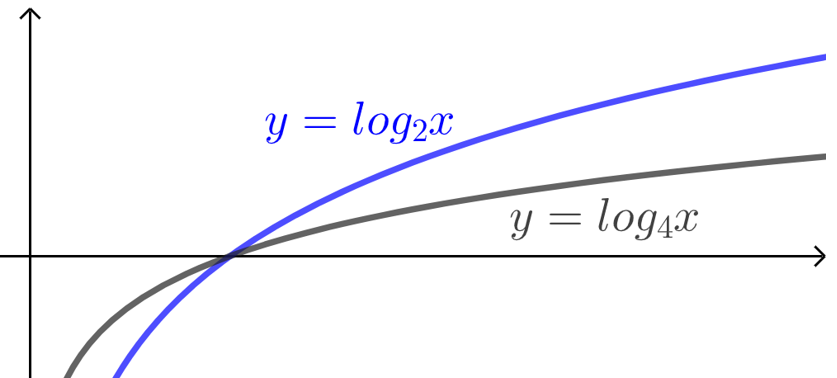
4 指数函数的增长速度
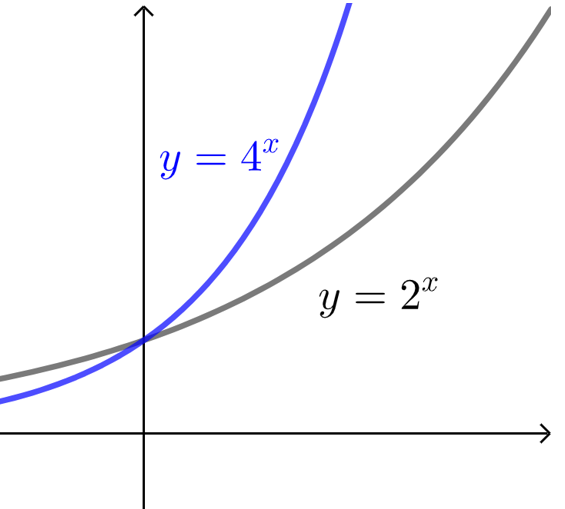
指数函数\(y=a^x (a>1)\)在区间\((0,+∞)\)上是增函数,其增长速度最快.
其底数\(a\)越大,增长的速度越快.
如 \(y=4^x\)比\(y=2^x\)的增长速度更快.当\(x<0\)时, \(y=4^x\)的函数值比 \(y=2^x\)小;
当\(x>0\)时, \(y=4^x\)的函数值比 \(y=2^x\)大,并且越来越大.
5 几类不同增长的函数模型的比较
(1)指数函数、对数函数、幂函数的增长趋势比较
| \(y=a^x (a>1)\) | \(y=log_ax (a>1)\) | \(y=x^n (n>0)\) | |
|---|---|---|---|
| 在区间\((0,+∞)\)的单调性 | 增函数 | 增函数 | 增函数 |
| 增长速度 | 先慢后快 | 先快后慢 | 相对平稳 |
| 图象变化 | 随\(x\)的增大逐渐加快增大 | 随\(x\)的增大逐渐减慢增大 | 随\(n\)的不同而不同 |
如 \(y=2^{x}, y=x^{2}, y=\log _{2} x\),
三个函数在\((0,+∞)\)上都是增函数,但它们的增速不一样,
我们列表看看,
| \(x\) | \(\dfrac{1}{4}\) | \(\dfrac{1}{2}\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) |
|---|---|---|---|---|---|---|---|---|---|
| \(y=2^x\) | \(≈1.2\) | \(≈1.4\) | \(2\) | \(4\) | \(8\) | \(16\) | \(32\) | \(64\) | \(128\) |
| \(y=x^2\) | \(≈0.06\) | \(≈0.25\) | \(1\) | \(4\) | \(9\) | \(16\) | \(25\) | \(36\) | \(49\) |
| \(y=log_2 x\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(≈1.6\) | \(2\) | \(≈2.3\) | \(≈2.6\) | \(≈2.8\) |
在同一坐标系内,作出函数图象,如下图,
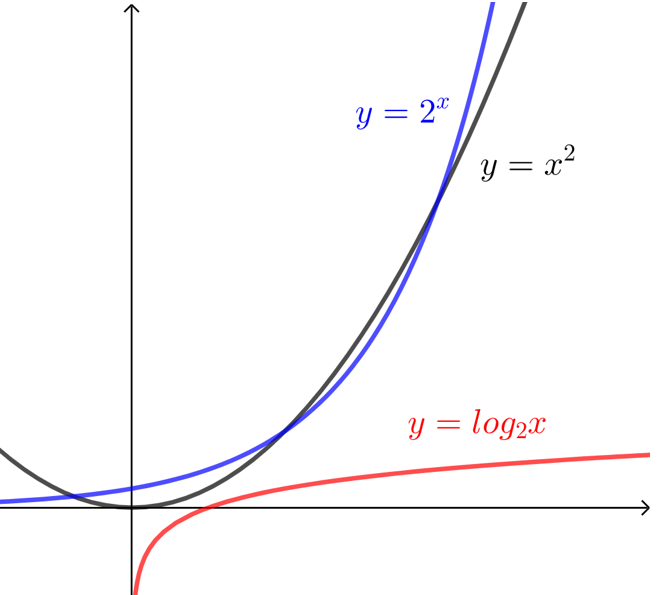
由图和表,易知对数函数\(y=log_2 x\)增长得很慢,指数函数\(y=2^x\)增长得很快,比幂函数\(y=x^2\)更快.而当0\(<x<4\)时, \(y=2^x\)的函数值有些比 \(y=x^2\)小;当\(x>4\)时, \(y=2^x\)的函数值比 \(y=x^2\)大,且相差越来越大.
综上所述,在区间\((0,+∞)\)上,尽管函数\(y=a^x (a>1)\),\(y=log_ax(a>1)\)和\(y=x^n (n>0)\)都是增函数,但它们的增长速度不同,而且不在同一个“档次”上.随着\(x\)的增大,\(y=a^x (a>1)\)的增长速度越来越快,会超过并远远大于\(y=x^n (n>0)\)的增长速度,而\(y=log_ax(a>1)\)的增长速度则会越来越慢,总会存在一个\(x_0\),当 \(x>x_0\),就有 \(\log _{a} x<x^{n}<a^{x}\).
【例】当\(x\)越来越大时,下列函数中,增长速度最快的应该是( )
A.\(y=100x\) \(\qquad \qquad\) B.\(y=\log_{100}x\) \(\qquad \qquad\) C. \(y=x^{100}\) \(\qquad \qquad\) D.\(y=100^x\)
解析 由于指数型函数的增长是爆炸式增长,则当\(x\)越来越大时,函数 \(y=100^x\)增长速度最快.
故选\(D\).
函数模型
1 函数模型
| 函数类型 | 解析式 |
|---|---|
| 一次函数 | \(y=ax+b(a≠0)\) |
| 二次函数 | \(y=ax^2+bx+ c (a≠0)\) |
| 指数函数 | \(y=a^x (a>0\)且\(a≠1)\) |
| 指数型函数 | \(y=k\cdot a^x (a>0\)且\(a≠1)\) |
| 对数函数 | \(y=log_a x (a>0\)且\(a≠1)\) |
| 对数型函数 | \(y=k\cdot log_a x (a>0\)且\(a≠1)\) |
| 幂函数 | \(y=x^n (n∈ N^*)\) |
| 幂函数型 | \(y=k⋅x^n (n∈ N^*)\) |
2 函数模型解决实际问题
通过收集数据直接去解决问题的一般过程如下:
第一步:收集数据.
第二步:根据收集到的数在平面直角坐标系内画出散点图.
第三步:根据点的分布特征,选择一个能刻画散点图特征的函数模型.
第四步:选择其中的几组数据求出函数模型.
第五步:将已知数据代入所求出的函数模型进行检验,看其是否符合实际.若不符合实际,则重复第三、四、五步;若符合实际,则进入下一步.
第六步:用求得的函数模型去解释实际问题.
基本方法
【题型1】不同函数模型的认识
【典题1】 某市某学校物理兴趣小组在实验测试中收集到一组数据如表所示:
| \(t\) | \(1.99\) | \(3.0\) | \(4.0\) | \(5.1\) | \(6.12\) |
|---|---|---|---|---|---|
| \(v\) | \(1.5\) | \(4.04\) | \(7.5\) | \(12\) | \(18.01\) |
用下列函数中的一个近似地表示这些数据满足的规律,其中最接近的一个是( )
A.\(v=log_2t\) \(\qquad \qquad\) B. \(v=\log _{\frac{1}{2}} t\) \(\qquad \qquad\) C. \(v=\dfrac{t^{2}-1}{2}\) \(\qquad \qquad\) D.\(v=2t-2\)
解析 方法1 由表可知:\(v\)是关于\(t\)的增函数;且增幅随\(t\)的增大而增大,故只有\(C\)满足要求.故选\(C\).
方法2 作出散点图,如图,
由函数拟合可知只有\(C\)满足要求.故选\(C\).

方法3 由表可知:\(v\)是关于\(t\)的增函数;故\(B\)不适合;
对于\(A\): \(\log _{2} 1.99 \approx 2, \log _{2} 3 \approx 0.3, \log _{2} 4=2\);故\(A\)不接近;
对于\(C\): \(\dfrac{1.99^{2}-1}{2} \approx 1.5, \quad \dfrac{3^{2}-1}{2}=4, \quad \dfrac{4^{2}-1}{2}=7.5\).故\(C\)接近;
对于\(D\):\(2×1.99-2=1.98\),\(2×3-2=4\),\(2×4-2=6\),\(2×5.1-2=8.2\),\(2×6.12-2=10.24\),故\(D\)不接近.
故选\(C\).
点拨
判断最佳函数模型,方法如下
① 根据数据的增减性和增幅,排除不符合的函数;
② 根据表格描点做出散点图,结合常见函数模型进行判断;
③ 代点法,把数值代入函数中,若数值偏离较远则排除.
巩固练习
1.试探究下列三个函数,当\(x\)足够大后,其增长速度最快的是\(\underline{\quad \quad}\) .
①\(y=10x^3\) \(\qquad \qquad\) ②\(y=100\cdot lgx\) \(\qquad \qquad\) ③ \(y=\dfrac{1}{100} \cdot 10^{x}\).
2.在一次数学实验中,运用图形计算器采集到如下一组数据:
| \(x\) | \(-2.0\) | \(-1.0\) | \(0\) | \(1.00\) | \(2.00\) | \(3.00\) |
|---|---|---|---|---|---|---|
| \(y\) | \(0.24\) | \(0.51\) | \(1\) | \(2.02\) | \(3.98\) | \(8.02\) |
则\(x,y\)的函数关系与下列哪类函数最接近?(其中\(a,b\)为待定系数)( )
A.\(y=a+bx\) \(\qquad \qquad\) B.\(y=b^x\) \(\qquad \qquad\) C. \(y=\dfrac{a}{x^{2}}+b\) \(\qquad \qquad\) D. \(y=\dfrac{b}{x}\)
3.某校为了规范教职工绩效考核制度,现准备拟定一函数用于根据当月评价分数\(x\)(正常情况\(0≤x≤100\),且教职工平均月评价分数在\(50\)分左右,若有突出贡献可以高于\(100\)分)计算当月绩效工资\(y\)元.要求绩效工资不低于\(500\)元,不设上限且让大部分教职工绩效工资在\(600\)元左右,另外绩效工资越低、越高人数要越少.则下列函数最符合要求的是( )
A.\(y=(x-50)^2+500\) \(\qquad \qquad \qquad\) B. \(y=10^{\frac{x}{25}}+500\)
C. \(y=\dfrac{1}{1000}(x-50)^{3}+625\) \(\qquad \qquad\) D. \(y=50[10+\lg (2 x+1)]\)
参考答案
-
答案 ③
解析 当\(x\)足够大时,函数\(y=10x^3\),是幂函数,其增长速度相比较不是最快的;
函数 \(y=100\cdot lgx\),是对数函数,其增长速度相比较是最慢的;
函数 \(y=\dfrac{1}{100} \cdot 10^{x}\),是指数函数,且底数大于\(1\),其增长速度相比较是最快的.
故答案为:③. -
答案 \(B\)
解析 散点图如图所示:

由散点图可知,此函数图象不是直线,排除\(A\)选项;此函数图象是“上升”的,
因此该函数为增函数,排除\(C,D\)选项,故选择\(B\). -
答案 \(C\)
解析 由题意知:
拟定函数应满足①是单调增函数,且先慢后快;
②在\(x=50\)左右增长缓慢,最小值为\(500\);
\(A\)中,\(y=(x-50)^2+500\)是先递减后增加,不符合要求;
\(B\)中, \(y=10^{\dfrac{x}{25}}+500\)是指数函数类型,是增长越来越快的,不符合要求;
\(C\)中, \(y=\dfrac{1}{1000}(x-50)^{3}+625\)是\(y=x^3\)的平移和伸缩变换而得,最符合题目要求
\(D\)中, \(y=50[10+\lg (2 x+1)]\)是对数函数类型,增长速度越来越慢,不符合要求;
故选:\(C\).
【题型2】不同函数模型的应用
【典题1】 牛顿冷却定律描述物体在常温环境下的温度变化:如果物体的初始温度为\(T_0\),则经过一定时间\(t\)分钟后的温度\(T\)满足 \(T-T_{a}=\left(\dfrac{1}{2}\right)^{\frac{t}{h}}\left(T_{0}-T_{a}\right)\), 称为半衰期,其中\(T_a\)是环境温度.若\(T_a=25^∘ C\),现有一杯\(80^∘ C\)的热水降至\(75^∘ C\)大约用时\(1\)分钟,那么水温从\(75^∘ C\)降至\(45^∘ C\),大约还需要( )(参考数据:\(lg2≈0.30\),\(lg11≈1.04\))
A.\(8\)分钟 \(\qquad \qquad\) B.\(9\)分钟 \(\qquad \qquad\) C.\(10\)分钟 \(\qquad \qquad\) D.\(11\)分钟
解析 由题意可得 \(75-25=\left(\dfrac{1}{2}\right)^{\frac{1}{h}}\), \(\therefore\left(\dfrac{1}{2}\right)^{\frac{1}{h}}=\dfrac{10}{11}\),
\(\therefore 45-25=\left(\dfrac{1}{2}\right)^{\frac{t}{h}}\) ,\(\therefore 20=50 \times\left[\left(\dfrac{1}{2}\right)^{\frac{1}{h}}\right]^{t}\)
\(\therefore\left(\dfrac{10}{11}\right)^{t}=\dfrac{2}{5}\),两边取常用对数得 \(\operatorname{tg} \dfrac{10}{11}=\lg \dfrac{2}{5}\),
\(\therefore t=\dfrac{\lg \dfrac{2}{5}}{\lg \dfrac{10}{11}}=\dfrac{\lg 2-\lg 5}{1-\lg 11}=\dfrac{2 \lg 2-1}{1-\lg 11} \approx \dfrac{2 \times 0.3-1}{1-1.04}=10\),
\(∴\)水温从\(75^∘ C\)降至\(45^∘ C\),大约还需要\(10\)分钟,
故选:\(C\).
点拨 求解指数幂的方程,两边取对数是常用方法.
【典题2】 假设有一套住房从2002年的\(20\)万元上涨到2012年的\(40\)万元.如表给出了两种价格增长方式,其中\(P_1\)是按直线上升的房价,\(P_2\)是按指数增长的房价,\(t\)是2002年以来经过的年数.
| \(t\) | \(0\) | \(5\) | \(10\) | \(15\) | \(20\) |
|---|---|---|---|---|---|
| \(P_1/\)万元 | \(20\) | \(40\) | |||
| \(P_2/\)万元 | \(20\) | \(40\) |
(1)求函数\(P_1=f(t)\)的解析式;
(2)求函数\(P_2=g(t)\)的解析式;
(3)完成上表空格中的数据,并在同一直角坐标系中画出两个函数的图象,然后比较两种价格增长方式的差异.
解析 (1)由题意可设\(P_1=f(t)=mt+n,(m≠0)\),
\(∵\)当\(t=0\)时,\(P_1=20\);当\(t=10\)时,\(P_1=40\),
\(\therefore\left\{\begin{array}{l}
n=20 \\
10 m+n=40
\end{array}\right.\),解得 \(\left\{\begin{array}{l}
m=2 \\
n=20
\end{array}\right.\),
\(∴P_1=f(t)=2t+20\);
(2)由题意可设\(P_2=g(t)=20(1+a\%)^t\),
\(∵\)当\(t=10\)时,\(P_2=40\),\(∴20(1+a\%)10=40\), \(\therefore 1+a \%=2^{\frac{1}{10}}\),
\(\therefore P_{2}=g(t)=20 \times 2^{\frac{t}{10}}\);
(3)表中数据如下:
| \(t\) | \(0\) | \(5\) | \(10\) | \(15\) | \(20\) |
|---|---|---|---|---|---|
| \(P_1/\)万元 | \(20\) | \(30\) | \(40\) | \(50\) | \(60\) |
| \(P_2/\)万元 | \(20\) | \(20 \sqrt{2}\) | \(40\) | \(40 \sqrt{2}\) | \(80\) |
在同一直角坐标系中画出两个函数的图象,如图所示:
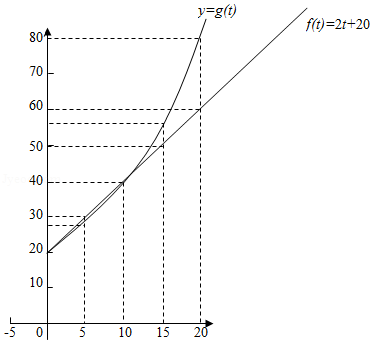
有图象可知,\(P_1=f(t)=2t+20\)呈直线增长,增长速度较慢;
\(P_{2}=g(t)=20 \times 2^{\frac{t}{10}}\)呈指数型增长,增长速度较快.
【典题3】某地为践行绿水青山就是金山银山的理念,大力开展植树造林.假设一片森林原来的面积为\(a\)亩,计划每年种植一些树苗,且森林面积的年增长率相同,当面积是原来的\(2\)倍时,所用时间是\(10\)年.
(1)求森林面积的年增长率;
(2)到今年为止,森林面积为原来的 \(\sqrt{2}\)倍,则该地已经植树造林多少年?
(3)为使森林面积至少达到\(6a\)亩至少需要植树造林多少年?
(参考数据:\(lg2=0.3010\),\(lg3=0.4771\))
解析 (1)设森林面积的年增长率为\(x\),则\(a(1+x)^{10}=2a\),解得 \(x=2^{\frac{1}{10}}-1\),
\(∴\)森林面积的年增长率为 \(2^{\frac{1}{10}}-1\);
(2)设已经植树造林\(n\)年,则由题意可知 \(a(1+x)^{n}=\sqrt{2} a\),
\(\therefore a \times 2^{\frac{n}{10}}=\sqrt{2} a\),\(∴n=5\),
\(∴\)已经植树造林\(5\)年;
(3)设为使森林面积至少达到\(6a\)亩至少需要植树造林\(m\)年,则 \(a(1+x)^{m} \geq 6 a\),
\(\therefore 2^{\frac{m}{10}} \geq 6\), \(\therefore \dfrac{m}{10} \geq \log _{2} 6=\dfrac{\lg 6}{\lg 2}=\dfrac{\lg 2+\lg 3}{\lg 2}\),
\(\therefore m \geq 10 \times \dfrac{\lg 2+\lg 3}{\lg 2} \approx 26\),
故为使森林面积至少达到\(6a\)亩至少需要植树造林\(26\)年.
巩固练习
1.(多选)边际函数是经济学中一个基本概念,在国防、医学、环保和经济管理等许多领域都有十分广泛的应用.函数\(f(x)\)的边际函数\(Mf(x)\)定义为\(Mf(x)=f(x+1)-f(x)\).某公司每月最多生产\(75\)台报警系统装置,生产\(x\)台\((x∈N^* )\)的收入函数\(R(x)=3000x-20x^2\) (单位:元),其成本函数为\(C(x)=500x+4000\) (单位,元),利润是收入与成本之差,设利润函数为\(P(x)\),则以下说法正确的是( )
A.\(P(x)\)取得最大值时每月产量为\(63\)台
B.边际利润函数的表达式为\(MP(x)=2480-40x(x∈N^* )\)
C.利润函数\(P(x)\)与边际利润函数\(MP(x)\)不具有相同的最大值
D.边际利润函数\(MP(x)\)说明随着产量的增加,每台利润与前一台利润差额在减少
2.(多选)为预防流感病毒,我校每天定时对教室进行喷洒消毒.当教室内每立方米药物含量超\(0.25mg\)时能有效杀灭病毒.已知教室内每立方米空气中的含药量\(y\)(单位:\(mg\))随时间\(x\)(单位:\(h\))的变化情况如图所示:在药物释放过程中,\(y\)与\(x\)成正比:药物释放完毕后,\(y\)与\(x\)的函数关系式为: \(y=\dfrac{a}{x}\)(\(a\)为常数),则下列说法正确的是 ( )
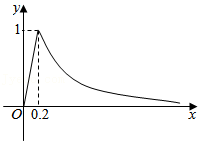
A.当\(0⩽x⩽0.2\)时,\(y=5x\)
B.当\(x>0.2\)时, \(y=\dfrac{1}{5 x}\)
C.教室内持续有效杀灭病毒时间为\(0.85\)小时
D.喷洒药物\(3\)分钟后才开始有效灭杀病毒
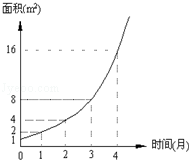
3.某地野生微甘菊的面积与时间的函数关系的图象,如图所示假设其关系为指数函数,并给出下列说法
①此指数函数的底数为\(2\);
②在第\(5\)个月时,野生微甘菊的面积就会超过\(30m^2\);
③设野生微甘菊蔓延到 \(2 m^{2}, 3 m^{2}, 6 m^{2}\)所需的时间分别为\(t_1,t_2,t_3\),则有\(t_1+t_2=t_3\);
④野生微甘菊在第\(1\)到第\(3\)个月之间蔓延的平均速度等于在第2到第4个月之间蔓延的平均速度
其中正确的说法有 \(\underline{\quad \quad}\)(请把正确说法的序号都填在横线上).
4.某地区今年1月,2月,3月患某种传染病的人数分别为\(42,48,52\).为了预测以后各月的患病人数,甲选择了模型\(y=ax^2+bx+c\),乙选择了模型\(y=pq^x+r\),其中\(y\)为患病人数,\(x\)为月份数,\(a,b,c,p,q,r\)都是常数.结果4月,5月,6月份的患病人数分别为\(54,57,58\).
(1)求\(a,b,c,p,q,r\)的值; \(\qquad \qquad\) (2)你认为谁选择的模型好.
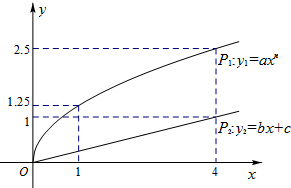
5.某企业拟共用\(10\)万元投资甲、乙两种商品.已知各投入\(x\)万元,甲、乙两种商品可分别获得\(y_1,y_2\)万元的利润,利润曲线\(P_1,P_2\)如图,仔细观察图象,为使投资获得最大利润,应怎样分配投资额,才能获最大利润.
参考答案
- 答案 \(BCD\)
解析 对于\(A\),\(P(x)=R(x)-C(x)=-20x^2+2500x-4000\),
二次函数\(P(x)\)的图象开口向下,对称轴为直线 \(x=\dfrac{2500}{40}=62.5\),
\(∵x∈N^*\),
\(∴P(x)\)取得最大值时每月产量为\(63\)台或\(62\)台,故\(A\)错误,
对于\(B\), \(M P(x)=P(x+1)-P(x)\)
\(=\left[-20(x+1)^{2}+2500(x+1)-4000\right]\)\(-\left(-20 x^{2}+2500 x-4000\right) =2480-40 x\left(x \in N^{*}\right)\),
故\(B\)正确,
对于\(C\), \(P(x)_{\max }=P(62)=P(63)=74120\),
\(∵\)函数\(MP(x)=2480-40x\)为减函数,则 \(M P(x)_{\max }=M P(1)=2440\),故\(C\)正确,
对于\(D\),因为函数\(MP(x)=2480-40x\)为减函数,
说明边际函数\(MP(x)\)说明随着产量的增加,每台利润与前一台利润差额在减少,故D正确.
故选:\(BCD\). - 答案 \(ABD\)
解析 对于\(A\),在药物释放过程中,设\(y=kx(k≠0)\),
将点\((0.2,1)\)代入\(y=kx\),解得\(k=5\),
故当\(0⩽x⩽0.2\)时,\(y=5x\),故\(A\)正确,
对于\(B\),\(∵\)药物释放完毕后,\(y\)与\(x\)的函数关系式为: \(y=\dfrac{a}{x}\)(\(a\)为常数),
\(∴\)将点\((0.2,1)\)代入 \(y=\dfrac{a}{x}\)(\(a\)为常数),解得\(a=0.2\),
故\(x>0.2\)时, \(y=\dfrac{1}{5 x}\),故\(B\)正确,
对于\(C\),令 \(y=\dfrac{1}{5 x} \geqslant \dfrac{1}{4}\),解得\(x \leqslant \dfrac{4}{5}<0.85\),故\(C\)错误,
对于\(D\),令\(5x=0.25\),解得\(x=0.05\)小时,即\(x=3\)分钟,故\(D\)正确,
故选:\(ABD\). - 答案 ①②③
解析 \(∵\)其关系为指数函数,图象过\((4,16)\)点,
\(∴\)指数函数的底数为\(2\),故①正确,
当\(t=5\)时,\(s=32>30\),故②正确
\(∵t_1=1\),\(t_2=log_23\),\(t_3=log_26\),
\(∴\)有\(t_1+t_2=t_3\),故③正确,
根据图象的变化快慢不同知④不正确,
综上可知①②③正确. - 答案 (1) \(a=-1\),\(b=9\),\(c=34\), \(p=-27\), \(q=\dfrac{2}{3}\),\(r=60\). (2) 乙模型
解析 (1)由甲模型:令\(y=f(x)=ax^2+bx+c\),
可得:\(a+b+c=42\),\(4a+2b+c=48\),\(9a+3b+c=52\),
解得 \(a=-1\),\(b=9\),\(c=34\).
由乙模型:设\(y=pq^x+r\),
可得:\(g(1)=pq+r=42\), \(g(2)=pq^2+r=48\),\(g(3)=pq^3+r=52\)
解得 \(p=-27\), \(q=\dfrac{2}{3}\),\(r=60\).
(2)由 (1)可得:\(f(x)=-x^2+9x+34\),
\(∴f(4)=-4^2+9×4+34=54\),
\(f(5)=-5^2+9×5+34=54<57\),
\(f(6)=-6^2+9×6+34=52<58\);
由乙模型可得: \(g(x)=-27 \cdot\left(\dfrac{2}{3}\right)^{x}+60\),
\(\because g(4)=54+\dfrac{2}{3} \approx 54\), \(g(5)=56+\dfrac{4}{9} \approx 56\), \(g(6)=57+\dfrac{17}{27} \approx 57\).
可得:\(g(4)、g(5)、g(6)\)比\(f(4)、f(5)、f(6)\)更接近真实值. - 答案 对甲产品投资 \(\dfrac{25}{4}\)万元,对乙产品投资 \(\dfrac{15}{4}\)万元时,可获最大利润 \(\dfrac{65}{16}\)万元
解析 投资为\(x\)万元,
甲、乙两产品获得的利润分别为\(g(x)、f(x)\)万元,
由题意,\(g(x)=k_1 x\), \(f(x)=k_{2} \sqrt{x}\),\((k_1,k_2≠0;x≥0)\)
又由图知\(g(1)=1.25\),\(f(4)=2.5\);
解得 \(\mathrm{k}_{1}=\dfrac{1}{4}\), \(k_{2}=\dfrac{5}{4}\),
\(\therefore g(x)=\dfrac{1}{4} x(x \geq 0)\);\(f(x)=\dfrac{5}{4} \sqrt{x}(x \geq 0)\)
再设对甲产品投资\(x\)万元,则对乙产品投资\((10-x)\)万元,
记企业获取的利润为\(y\)万元,
则 \(y=\dfrac{1}{4}(10-x)+\dfrac{5}{4} \sqrt{x}(x \geq 0)\)
设 \(\sqrt{x}=t\),则 \(x=t^{2},(0 \leq t \leq \sqrt{10})\)
\(\therefore y=-\dfrac{1}{4}\left(t-\dfrac{5}{2}\right)^{2}+\dfrac{65}{16}\),
当 \(t=\dfrac{5}{2}\)也即 \(x=\dfrac{25}{4}\)时,\(y\)取最大值 \(\dfrac{65}{16}\)
答:对甲产品投资 \(\dfrac{25}{4}\)万元,对乙产品投资 \(\dfrac{15}{4}\)万元时,可获最大利润 \(\dfrac{65}{16}\)万元.
分层练习
【A组---基础题】
1.下列函数中,随\(x\)的增大,其增大速度最快的是( )
A.\(y=0.001e^x\) \(\qquad \qquad\) B.\(y=1000\ln x\) \(\qquad \qquad\) C.\(y=x^{1000}\) \(\qquad \qquad\) D.\(y=1000 \cdot 2^x\)
2.下图所示的是一份统计图表,根据此图表得到的以下说法中,正确的有 ( )
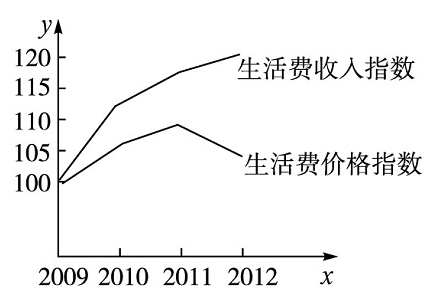
(1)这几年人民生活水平逐年得到提高;
(2)人民生活费收入增长最快的一年是\(2009\)年;
(3)生活费价格指数上涨速度最快的一年是\(2010\)年;
(4)虽然\(2011\)年生活费收入增长是缓慢的,但由于生活费价格指数也略有降低,因而人民生活有较大的改善.
A.\(1\)项 \(\qquad \qquad\) B.\(2\)项 \(\qquad \qquad\) C.\(3\)项 \(\qquad \qquad\) D.\(4\)项
3.下列函数关系中,可以看着是指数型函数\(y=ka^x (k∈R,a>0\)且\(a≠1)\)模型的是( )
A.竖直向上发射的信号弹,从发射到落回地面,信号弹的高度与时间的关系(不计空气阻力).
B.我国人口年自然增长率为\(1\%\),这样我国人口总数随年份的变化关系.
C.如果某人\(ts\)内骑车行进了\(1km\),那么此人骑车的平均速度\(v\)与时间\(t\)的函数关系.
D.信件的邮资与其重量间的函数关系.
4.2003年至2015年北京市电影放映场次(单位:万次)的情况如图所示,将年份作为自变量\(x\),当年电影放映场次作为函数值\(y\),下列函数模型中,最不适合近似描述这13年间电影放映场次逐年变化规律的函数是( )

A.\(f(x)=ax^2+bx+c\) \(\qquad \qquad\) B.\(f(x)=ax+b\) \(\qquad \qquad\) C.\(f(x)=e^{a x+b}\) \(\qquad \qquad\) D. \(f(x)=\dfrac{b}{a x}\)
5.(多选)某市出租车收费标准如下:起步价为\(8\)元,起步里程为\(3km\)(不超过\(3km\)按起步价付费);超过\(3km\)但不超过\(8km\)时,超过部分按每千米\(2.15\)元收费;超过\(8km\)时,超过部分按每千米\(2.85\)元收费,另每次乘坐需付燃油附加费\(1\)元.下列结论正确的是 ( )
A.出租车行驶\(2km\),乘客需付费\(8\)元
B.出租车行驶\(10km\),乘客需付费\(25.45\)元
C.某人乘出租车行驶\(5km\)两次的费用超过他乘出租车行驶\(10km\)一次的费用
D.某人乘坐一次出租车付费\(22.6\)元,则此次出租车行驶了\(9km\)
6.(多选)某医药研究机构开发了一种新药,据监测,如果患者每次按规定的剂量注射该药物,注射后每毫升血液中的含药量\(y\) (微克)与时间\(t\)(小时)之间的关系近似满足如图所示的曲线.据进一步测定,当每毫升血液中含药量不少于\(0.125\)微克时,治疗该病有效,则 ( )

A.\(a=3\)
B.注射一次治疗该病的有效时间长度为\(6\)小时
C.注射该药物 \(\dfrac{1}{8}\)小时后每毫升血液中的含药量为\(0.4\)微克
D.注射一次治疗该病的有效时间长度为 \(5 \dfrac{31}{32}\)小时
7.某科研小组研究了一种常见树的生长周期中前\(10\)年生长规律,统计显示,生长\(3\)年的树高为 \(\dfrac{7}{3}\)米,如图所示的散点图记录了样本树的生长时间\(t\)(年 与树高y (米 之间的关系.请你据此判断,在下列函数模型:① \(y=\sqrt{t}+a\),②\(y=2^t-a\),③\(y=a+log_3t\)中(其中\(a\)为正的常数),拟合生长年数与树高的关系最好的是\(\underline{\quad \quad}\) (填写序号),估计该树生长\(9\)年后的树高为\(\underline{\quad \quad}\) 米.

8.生物入侵是指生物由原生存地侵入到另一个新的环境,从而对入侵地的生态系统造成危害的现象.若某入侵物种的个体平均繁殖数量为 ,一年四季均可繁殖,繁殖间隔 为相邻两代间繁殖所需的平均时间.在物种入侵初期,可用对数模型\(K(n)=λ\cdot \ln n(λ\)为常数)来描述该物种累计繁殖数量\(n\)与入侵时间\(K\) (单位:天)之间的对应关系,且 \(Q=\dfrac{T}{\lambda}+1\),在物种入侵初期,基于现有数据得出\(Q=6,T=50\).据此估计该物种累计繁殖数量比初始累计繁殖数量增加11倍所需要的时间为 \(\underline{\quad \quad}\) 天.\((ln2≈0.69,ln3≈1.10)\)
9.某工厂生产一种产品,根据预测可知,该产品的产量平稳增长,记2015年为第1年,第\(x\)年与年产量\(f(x)\)(万件)之间的关系如表所示:
| \(x\) | \(1\) | \(2\) | \(3\) | \(4\) |
|---|---|---|---|---|
| \(f(x)\) | \(4.00\) | \(5.52\) | \(7.00\) | \(8.49\) |
现有三种函数模型:\(f(x)=ax+b\),\(f(x)=a×2^x+b\),\(f(x)=log_{0.5}x+a\)
(1)找出你认为最适合的函数模型,并说明理由,然后选取\(x=1,3\)这两年的数据求出相应的函数解析式;
(2)因受市场环境的影响,2020年的年产量估计要比预计减少\(30\%\),试根据所建立的函数模型,估计2020年的年产量.
10.1766年;人类已经发现的太阳系中的行星有金星、地球、火星、木星和土星.德国的一位中学教师戴维一提丢斯在研究了各行星离太阳的距离(单位:AU,AU是天文学中计量天体之间距离的一种单位)的排列规律后,预测在火星和木星之间应该还有一颗未被发现的行星存在,并按离太阳的距离从小到大列出了如表所示的数据:
| 行星编号\((x)\) | 1(金星) | 2(地球) | 3(火星) | 4 (谷神星) | 5(木星) | 6(土星) |
|---|---|---|---|---|---|---|
| 离太阳的距离\((y)\) | \(0.7\) | \(1.0\) | \(1.6\) | \(5.2\) | \(10.0\) |
受他的启发,意大利天文学家皮亚齐于\(1801\)年终于发现了位于火星和木星之间的谷神星.
(1)为了描述行星离太阳的距离\(y\)与行星编号之间的关系,根据表中已有的数据画出散点图,并根据散点图的分布状况,从以下三种模型中选出你认为最符合实际的一种函数模型(直接给出结论即可);
①\(y=ax+b\);②\(y=a\cdot b^x+c(b>1)\);③\(y=a\cdot log_bx+c(b>1)\).
(2)根据你的选择,依表中前几组数据求出函数解析式,并用剩下的数据检验模型的吻合情况;
(3)请用你求得的模型,计算谷神星离太阳的距离.
参考答案
- 答案 \(A\)
解析 在对数函数,幂函数,指数函数中,指数函数的增长速度最快,
故排除\(B,C\);指数函数中,底数越大,增长速度越快,故选:\(A\). - 答案 \(C\)
解析 由题意,“生活费收入指数”减去“生活费价格指数”的差是逐年增大的,故(1)正确;
“生活费收入指数”在\(2009~2010\)年最陡,故(2)正确;
“生活费价格指数”在\(2010~2011\)年最平缓,故(3)不正确;
由于“生活费价格指数”略呈下降,而“生活费收入指数”曲线呈上升趋势,故(4)正确.
故选\(C\). - 答案 \(B\)
解析 \(A\):竖直向上发射的信号弹,从发射到落回地面,信号弹的高度与时间的关系,
是二次函数关系;
\(B\):我国人口年自然增长率为\(1\%\),这样我国人口总数随年份的变化关系,是指数型函数关系;
\(C\):如果某人\(ts\)内骑车行进了\(1km\),那么此人骑车的平均速度\(v\)与时间\(t\)的函数关系,是反比例函数关系;
\(D\):信件的邮资与其重量间的函数关系,是正比例函数关系.
故选\(B\). - 答案 \(D\)
解析 由图象可知在第一象限内,\(y\)是关于\(x\)的增函数,
当 \(\dfrac{b}{a}>0\)时, \(f(x)=\dfrac{b}{a x}\)在第一象限内是减函数,
当 \(\dfrac{b}{a}<0\)时, \(f(x)=\dfrac{b}{a x}\)在第一象限内没有图象,
故 \(f(x)=\dfrac{b}{a x}\)最不适合.
故选:\(D\). - 答案 \(BCD\)
解析 对于\(A\),出租车行驶\(2km\),乘客需付起步价\(8\)元和燃油附加费1元,共\(9\)元,故\(A\)错误,
对于\(B\),出租车行驶 ,乘客需付费\(8+2.15×5+2.85×(10-8)+1=25.45\)元,故\(B\)正确,
对于\(C\),乘出租车行驶 ,乘客需付费\(8+2×2.15+1=13.3\) 元 ,
乘坐两次需付费\(26.6\)元,\(26.6>25.45\),故\(C\)正确,
对于\(D\),设出租车行驶\(xkm\)时,付费\(y\)元,由\(8+5×2.15+1=19.75<22.6\),
则\(x>8\),
故\(y=8+2.15×5+2.85(x-8)+1=22.6\),解得\(x=9\),,故\(D\)正确.
故选:\(BCD\). - 答案 \(AD\)
解析 由函数图像可知 \(y=\left\{\begin{array}{l} 4 t(0 \leqslant t<1) \\ \left(\dfrac{1}{2}\right)^{t-a}(1 \leqslant t) \end{array}\right.\),
当\(t=1\)时,\(y=4\),即 \(\left(\dfrac{1}{2}\right)^{1-a}=4\),解得\(a=3\),
\(\therefore y=\left\{\begin{array}{l} 4 t(0 \leqslant t<1) \\ \left(\dfrac{1}{2}\right)^{t-3}(1 \leqslant t) \end{array}\right.\),故\(A\)正确,
药物刚好起效的时间,当\(4t⩾0.125\),即 \(t \geqslant \dfrac{1}{32}\),
且药物刚好失效的时间 \(\left(\dfrac{1}{2}\right)^{t-3} \geqslant 0.125\),解得\(t⩽6\),
故药物的有效时间不到\(6\)个小时,故\(B\)错误,
注射该药物 \(\dfrac{1}{8}\)小时后每毫升血液含药量为 \(4 \times \dfrac{1}{8}=0.5\)微克,故\(C\)错误,
由B选项的分析可知,药物有效时长为 \(6-\dfrac{1}{32}=5 \dfrac{31}{32}\)小时,故\(D\)正确,
故选:\(AD\). - 答案 ③; \(\dfrac{10}{3}\)
解析 由三种函数的函数性质,以及散点图的特征,拟合生长年数与树高的关系最好的是③,
又因为生长3年的树高为 \(\dfrac{7}{3}\)米,所以 \(\dfrac{7}{3}=a+\log _{3} 3\),解得 \(a=\dfrac{4}{3}\),
所以拟合函数为 \(y=\dfrac{4}{3}+\log _{3} t\),当\(t=9\)时, \(y=\dfrac{4}{3}+\log _{3} 9=\dfrac{10}{3}\).
故答案为:③; \(\dfrac{10}{3}\). - 答案 \(24.8\)
解析 \(∵Q=\frac{T}{\lambda}+1\),\(Q=6\),\(T=50\),
\(\therefore 6=\dfrac{50}{\lambda}+1\),\(∴λ=10\),
设初始时间为\(K_1\),初始累计繁殖数量为\(n\),累计繁殖数量增加\(11\)倍后的时间为\(K_2\),
则 \(K_{2}-K_{1}=\lambda \ln (12 n)-\lambda \ln n=10(2 \ln 2+\ln 3) \approx 24.8\)(天) ,
故答案为:\(24.8\). - 答案 (1) \(f(x)=\dfrac{3}{2} x+\dfrac{5}{2}\) (2) \(8.05\)
解析 (1)最适合的函数模型是:\(f(x)=ax+b\),理由如下:
若模型为\(f(x)=a×2^x+b\),把点\((1,4)\),\((3,7)\)代入可求 \(a=\dfrac{1}{2}\),\(b=3\),
\(∴f(x)=2^{x-1}+3\),当\(x=4\)时,\(f(4)=11\),与已知相差太大,不符合,
若模型为 \(f(x)=log_{0.5}x+a\),则\(f(x)\)是减函数,与已知不符合,
由已知得 \(\left\{\begin{array}{l} a+b=4 \\ 3 a+b=7 \end{array}\right.\),解得 \(\left\{\begin{array}{l} a=\dfrac{3}{2} \\ b=\dfrac{5}{2} \end{array}\right.\),
\(\therefore f(x)=\dfrac{3}{2} x+\dfrac{5}{2}\);
(2)2020年的预计年产量为\(f(6)=11.5\),
∴2020年的实际年产量为:\(11.5×(1-0.3)=8.05\). - 答案 (1) ② \(\qquad\) (2) \(y=\dfrac{3}{20} \times 2^{x}+\dfrac{2}{5}\) \(\qquad\) (3)\(2.8\)
解析 (1)散点图如图所示:
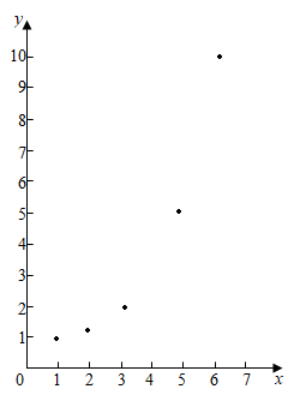
根据散点图的分布状况,选函数模型;②\(∵y=a\cdot b^x+c(b>1)\),最符合实际;
(2)\(∵y=a\cdot b^x+c(b>1)\),带入数据\((1,0.7)\),\((2,1)\),\((3,1.6)\),
得 \(\left\{\begin{array}{l} a \cdot b+c=0.7 \\ a \cdot b^{2}+c=1 \\ a \cdot b^{3}+c=1.6 \end{array}\right.\),解得 \(\left\{\begin{array}{l} a=\dfrac{3}{20} \\ b=2 \\ c=\dfrac{2}{5} \end{array}\right.\),
\(∴\)函数解析式为 \(y=\dfrac{3}{20} \times 2^{x}+\dfrac{2}{5}\),
当\(x=5\)时,\(y=5.2\);当\(x=6\)时,\(y=10\),刚好符合;
(3)\(∵\)函数解析式为 \(y=\dfrac{3}{20} \times 2^{x}+\dfrac{2}{5}\),
\(∴\)当\(x=4\)时,\(y=2.8\),
\(∴\)谷神星离太阳的距离为\(2.8\)天文单位.
【B组---提高题】
1.(多选)小明从家里到学校行走的路程\(S\)与时间\(t\)的函数关系表示如图,记\(t\)时刻的瞬时速度为\(V(t)\),区间\([0,t_1 ]\),\([0,t_2 ]\),\([t_1, t_2]\)上的平均速度分别为\(V_1\),\(V_2\),\(V_3\),则下列判断正确的有( )

A.\(V_1<V_2<V_3\)
B. \(\dfrac{V_1+V_3}{2}>V_2\)
C.对于\(V_i (i=1,2,3)\),存在\(m_i∈(0,t_2 )\),使得\(V(m_i )=V_i\)
D.整个过程小明行走的速度一直在加快
2.函数\(y=x^2\)与函数\(y=x\lg x\)在区间\((0,+∞)\)上增长较快的一个是\(\underline{\quad \quad}\).
3.某同学从\(A\)地跑步到\(B\)地,随路程的增加速度减小.若以\(y\)表示该同学离\(B\)地的距离,\(x\)表示出发后的时间,则下列图象中较符合该同学走法的是\(\underline{\quad \quad}\).(填序号)
 \(\qquad\)
\(\qquad\) 
4.商品批发市场中,某商品的定价每天随市场波动,甲乙两名采购员在每月的同一天去该市场购买同一种商品,甲每次购买\(a\)公斤,乙每次购买\(b\)元(\(a,b\)互不相等),该方案实施\(2\)次后\(\underline{\quad \quad}\)的购买方案平均价格更低(填“甲”或“乙”
5.某厂家拟在\(2008\)年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量) 万件与年促销费用\(m\)万元\((m⩾0)\)满足 \(x=3-\dfrac{k}{m+1}\)(\(k\)为常数),如果不搞促销活动,则该产品的年销售量只能是\(1\)万件,已知2008年生产该产品的固定投入为\(8\)万元,每生产\(1\)万件该产品需要再投入\(16\)万元.厂家将每件产品的销售价格定为每件产品年平均成本的\(1.5\)倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
(1)将\(2008\)年该产品的利润\(y\)万元表示为年促销费用\(m\)万元的函数;
(2)该厂家\(2008\)年的促销费用投入多少万元时,厂家的利润最大?
参考答案
-
答案 \(ABC\)
解析 由题意可知; \(V_1=\dfrac{\dfrac{s_0}{2}-0}{t_1-0}=\dfrac{s_0}{2 t_1}\), \(V_2=\dfrac{s_0-0}{t_2-0}=\dfrac{s_0}{t_2}\), \(V_3=\dfrac{s_0-\dfrac{s_0}{2}}{t_2-t_1}=\dfrac{s_0}{2\left(t_2-t_1\right)}\),
由图像可知\(t_1<t_2\)且\(2t_1>t_2\),
因此 \(V_1=\dfrac{S_0}{2 t_1}<V_2=\dfrac{S_0}{t_2}\) ,\(t_2-2(t_2-t_1 )=2t_1-t_2>0\),
所以\(t_2>2(t_2-t_1 )\),因此 \(V_2=\dfrac{S_0}{t_2}<V_3=\dfrac{S_0}{2\left(t_2-t_1\right)}\) ,此时\(V_1<V_2<V_3\),故\(A\)正确;
由 \(V_1+V_3-2 V_3=S_0\left(\dfrac{1}{2 t_1}+\dfrac{1}{2\left(t_2-t_1\right)}-\dfrac{2}{t_2}\right)\),
可化为 \(\dfrac{t_2}{2 t_1\left(t_2-t_1\right)}-\dfrac{2}{t_2}=\dfrac{t_2^2-4 t_1\left(t_2-t_1\right)}{2 t_1 t_2\left(t_2-t_1\right)}=\dfrac{\left(t_2-t_1\right)^2}{2 t_1 t_2\left(t_2-t_1\right)}>0\),故 \(\dfrac{V_1+V_3}{2}>V_2\),故\(B\)正确;
由图像可知,直线与曲线的交点为 \(\left(t_1, \dfrac{S_0}{2}\right)\),
故存在\(m_i∈(0,t_2 )\),使得\(V(m_i )=V_i\),即当\(m_i=t_1\)时,\(V(V_1 )=V_1\),故\(C\)正确;
\(t\)时刻的瞬时速度为\(V(t)\),判断平均速度的快慢,可以看整个曲线在各点处的切线方程的斜率,
由图像可知,当\(t=t_1\)时,切线方程的斜率最大,故而在此时,平均速度最快,故\(D\)不正确.
故选:\(ABC\). -
答案 \(y=x^2\)
解析 幂函数的增长速度要比对数函数快,故答案为:\(y=x^2\). -
答案 ③
解析 高一的学生的讲解思路:取一段固定时间内的路程变化就是速度变化了;学了导数后,可知图像的切线斜率绝对值就是速度了. -
答案 乙
解析 设每次购买时商品的价格分别为\(x\)元 公斤、\(y\)元 公斤\((x,y>0)\),
则甲的平均价格为 \(\dfrac{a x+a y}{2 a}=\dfrac{x+y}{2}\);乙的平均价格为 \(\dfrac{2 b}{\dfrac{b}{x}+\dfrac{b}{y}}=\dfrac{2 x y}{x+y}\),
因为\(x\),\(y>0\),所以 \(\dfrac{x+y}{2} \geq \dfrac{2 \sqrt{x y}}{2}=\sqrt{x y}\);
\(\dfrac{2 x y}{x+y} \leqslant \dfrac{2 x y}{2 \sqrt{x y}}=\sqrt{x y}\) (当\(x=y\)时取"\(=\)"号),
所以 \(\dfrac{x+y}{2} \geqslant \dfrac{2 x y}{x+y}\)(当\(x=y\)时取"\(=\)"号),
故乙的平均价格更低.故答案为:乙. -
答案 (1) \(y=-\left[\dfrac{16}{m+1}+(m+1)\right]+29(m \geqslant 0)\) \(\qquad\) (2) \(3\)
解析 (1)由题意可知当\(m=0\)时,\(x=1\) (万件),\(∴1=3-k\),即\(k=2\),
\(\therefore x=3-\dfrac{2}{m+1}\),
每件产品的销售价格为 \(1.5 \times \dfrac{8+16 x}{x}\)(元) ,
\(∴2008\)年的利润 \(y=x\left[1.5 \times \dfrac{8+16 x}{x}\right]-(8+16 x+m)\)
\(=4+8 x-m=4+8\left(3-\dfrac{2}{m+1}\right)-m\)\(=-\left[\dfrac{16}{m+1}+(m+1)\right]+29(m \geqslant 0)\);
(2)当\(m⩾0\)时, \(\dfrac{16}{m+1}+(m+1) \geqslant 2 \sqrt{\dfrac{16}{m+1} \cdot(m+1)}=8\),
\(∴y⩽-8+29=21\),
当且仅当 \(\dfrac{16}{m+1}=m+1\),即\(m=3\)(万元)时, \(y_{\max }=21\) (万元).
答:该厂家2008年的促销费用投入\(3\)万元时,厂家的利润最大,最大为\(21\)万元.
【C组---拓展题】
1.新冠肺炎疫情造成医用防护服短缺,某地政府决定为防护服生产企业\(A\)公司扩大生产提供\(x(x∈[0,10])\)(万元)的专项补贴,并以每套\(80\)元的价格收购其生产的全部防护服.\(A\)公司在收到政府\(x\)(万元)补贴后,防护服产量将增加到 \(t=k \cdot\left(6-\dfrac{12}{x+4}\right)\)(万件),其中\(k\)为工厂工人的复工率\((k∈[0,5.1])\).\(A\)公司生产\(t\)万件防护服还需投入成本\((20+8x+50t)\)(万元).
(1)将\(A\)公司生产防护服的利润\(y\)(万元)表示为补贴\(x\)(万元)的函数;
(2)对任意的 \(x∈[0,10]\),当复工率\(k\)达到多少时,\(A\)公司才能不产生亏损?(精确到\(0.01\)).
参考答案
- 答案 (1) \(y=180 k-\dfrac{360 k}{x+4}-8 x-20\),\(x∈[0,10]\) (2) \(0.65\)
解析 (1) \(y=80 t-(20+8 x+50 t)=30 t-20-8 x\)
\(=30 k\left(6-\dfrac{12}{x+4}\right)-20-8 x=180 k-\dfrac{360 k}{x+4}-8 x-20\), \(x \in[0,10]\).
(2)若对任意的 \(x \in[0,10]\),公司都不产生亏损,
则 \(180 k-\dfrac{360 k}{x+4}-8 x-20 \geq 0\)在 \(x \in[0,10]\)恒成立,
即 \(k \geq \dfrac{1}{45} \cdot \dfrac{(x+4)(2 x+5)}{x+2}\), (分离参数法)
记\(t=x+2\),则\(t∈[2,12]\),
此时 \(\dfrac{(x+4)(2 x+5)}{x+2}=\dfrac{(t+2)(2 t+1)}{t}=2 t+\dfrac{2}{t}+5\),
由于函数 \(f(t)=2 t+\dfrac{2}{t}+5\)在\(t∈[2,12]\)单调递增,(对勾函数)
所以当\(t∈[2,12]\)时, \(f_{\max }(t)=f(12)=29+\dfrac{1}{6} \approx 29.167\),
\(\therefore k \geq \dfrac{1}{45} \times 29.167 \approx 0.648\),
即当工厂工人的复工率达到\(0.65\)时,对任意的\(x∈[0,10]\),公司都不产生亏损.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号