4.5.1 函数的零点与方程的解
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
【基础过关系列】2022-2023学年高一数学上学期同步知识点剖析精品讲义(人教A版2019）
\({\color{Red}{ 跟贵哥学数学，so \quad easy！}}\)
必修第一册同步巩固，难度2颗星！
基础知识
函数的零点
1 函数零点的概念
对于函数\(y=f(x)\)，使\(f(x)=0\)的实数\(x\)叫做函数的零点.
注 零点是个数，不是个点.
【例】函数\(f(x)=x-1\)的零点是\(\underline{\quad \quad}\).
解析 \(∵\)方程\(x-1=0\)的解是\(x=1\)，\(∴\)函数\(f(x)=x-1\)的零点是\(1\).
2 方程根与函数零点的关系
方程\(f(x)=0\)有实数根\(x_0\)
\(⇔\)函数\(y=f(x)\)有零点\(x_0\)
\(⇔\)函数\(y=f(x)\)的图象与\(x\)轴有交点，且交点横坐标为\(x_0\).
如 方程\(2^x-4=0\)的实数根是\(x=2\)，
函数\(f(x)=2^x-4\)与\(x\)轴的交点横坐标是\(2\)，
函数\(f(x)=2^x-4\)的零点是\(2\)，而不是\((2 ,0)\).
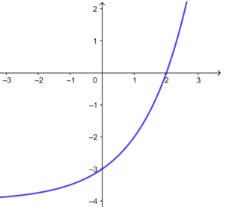
拓展
方程\(f(x)=g(x)\)有实数根\(x_0⇔\)函数\(y=f(x)\)与函数\(y=g(x)\)有交点，且交点横坐标为\(x_0\).
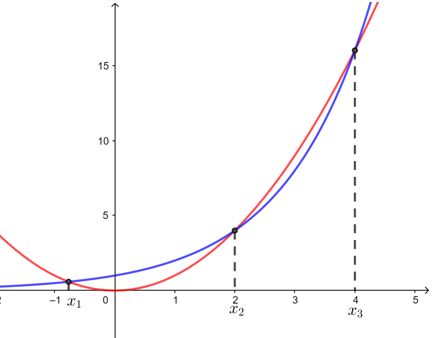
【例】 研究方程 \(x^2-2^x=0\)的解.
解析 方程 \(x^2-2^x=0\)的实数根\(⇔\)函数\(f(x)=x^2\)与函数\(g(x)=2^x\)的交点横坐标，
如图较容易得到，方程 \(x^2-2^x=0\)实数根有\(3\)个\(x_1∈(-1 ,0)\) ,\(x_2=2\) ,\(x_3=4\).
求函数零点方法
① (代数法) 求方程\(f(x)=0\)的实数根.
② (几何法) 利用函数的图象，根据函数的性质判断零点是否存在或找出零点位置.
函数零点存在定理
如果函数\(y=f(x)\)在\([a ,b]\)上的图象是连续不断的，且\(f(a)f(b)<0\)，那么函数\(y=f(x)\)在\((a ,b)\)至少有一个零点\(c\)，即存在\(c∈(a ,b)\)，使得\(f(c)=0\)，这个\(c\)也就是方程\(f(x)=0\)的解.
【例】研究函数 \(f(x)=x^3+x^2-1\)在\((0,1)\)上的零点个数.
解析 \(∵y=f(x)\)是连续函数，且\(f(0)f(1)=-1×1=-1<0\)，
\(∴\)由函数零点存在定理可得，\(y=f(x)\)在\((0,1)\)上至少存在一个零点，
而函数\(y=f(x)\)在\((0,1)\)又是增函数，
故函数 \(f(x)=x^3+x^2-1\)在\((0,1)\)上只有一个零点.
基本方法
【题型1】求(或判断)函数的零点
【典题1】 下列函数中只有一个零点的是( )
A． \(y=x^{-1}\) \(\qquad \qquad\) B．\(y=x^2+7x+6\) \(\qquad \qquad\) C．\(y=2^x-1\) \(\qquad \qquad\) D．\(y=\lg |x|\)
解析 方法1 解方程
对于\(A\)，方程 \(x^{-1}=0 \Rightarrow \dfrac{1}{x}=0\)无解，即函数 \(y=x^{-1}\)无零点；
对于\(B\)，方程\(x^2+7x+6=0\)，解得\(x=-1\)或\(－6\)，即函数\(y=x^2+7x+6\)有\(2\)个零点；
对于\(C\)，方程\(2x-1=0\)，解得\(x=0\)，即函数\(y=2^x-1\)只有\(1\)个零点；
对于\(D\)，方程\(\lg|x|=0\)，解得\(x=±1\)， 即函数\(y=\lg|x|\)有\(2\)个零点.
故选\(C\).
方法2 图象法
画出\(4\)个函数的图象如下
\(A\). 
\(\qquad \qquad\) \(B\). 
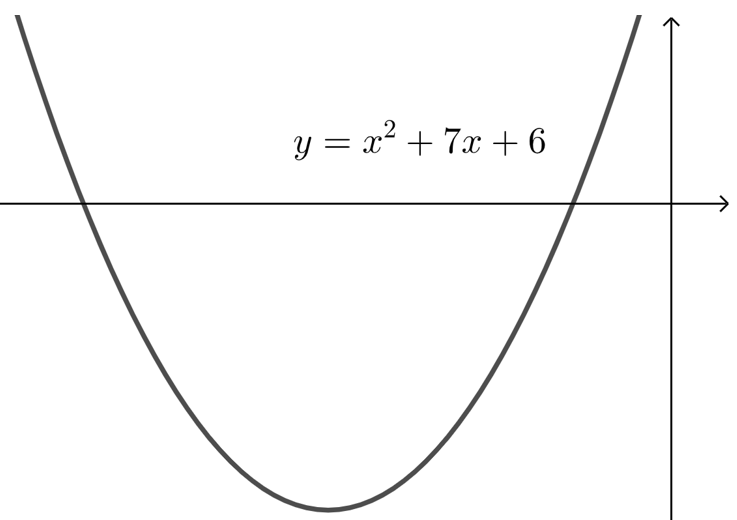
\(C\).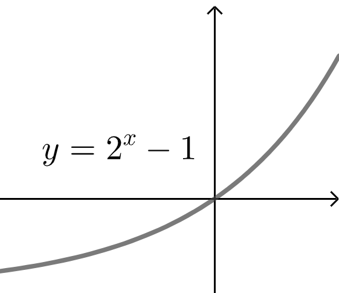
\(\qquad \qquad\) \(D\).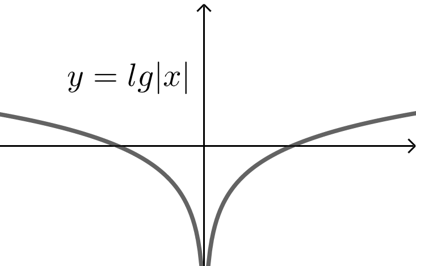
故选\(C\).
点拨
求函数零点方法
① 代数法：求方程\(f(x)=0\)的实数根.
② 几何法：利用函数的图象，根据函数的性质判断零点是否存在或找出零点位置.
【典题2】 函数\(f(x)=log_2 (x+4)-2^x\)的零点的情况是( )
A．仅有一个或\(0\)个零点 \(\qquad \qquad\) B．有两个正零点 \(\qquad \qquad\) C．有一正零点和一负零点 \(\qquad \qquad\) D．有两个负零点
解析 函数\(f(x)=log_2 (x+4)-2^x\)的零点的情况
等价于方程\(log_2 (x+4)-2^x=0\)的解的情况
等价于方程\(log_2 (x+4)=2^x\)的解的情况
等价于函数\(y=log_2(x+4)\)与\(y=2^x\)的交点的情况，
作函数\(y=log_2(x+4)\)与\(y=2^x\)的图象如下，
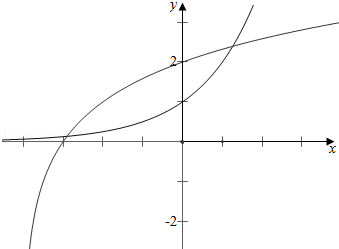
\(∵\)函数\(y=log_2(x+4)\)与\(y=2^x\)的图象有两个交点，且在\(y\)轴的两侧，
故选：\(C\)．
点拨
1.方程与函数的关系
方程\(f(x)=g(x)\)有实数根\(x_0⇔\)函数\(y=f(x)\)与函数\(y=g(x)\)有交点，且交点横坐标为\(x_0\).
2.对于该题型，需要提高构造函数的技巧.
巩固练习
1.判断下列函 数是否存在零点，如果存在，请求出．
(1) \(f(x)=\dfrac{x+3}{x}\)；\(\qquad \qquad\) (2) \(f(x)=1-log_3 x\)．
2.下列函数中，是偶函数且不存在零点的是( )
A．\(y=x^2\) \(\qquad \qquad\) B． \(y=\sqrt{x}\) \(\qquad \qquad\) C．\(y=\log_2x\) \(\qquad \qquad\) D． \(y=-\left(\dfrac{1}{2}\right)^{|x|}\)
3.已知函数 \(f(x)=\left\{\begin{array}{l}
|\ln x|, \quad x>0 \\
-2 x(x+2), \quad x \leq 0
\end{array}\right.\)，则函数\(y=f(x)－3\)的零点个数是\(\underline{\quad \quad}\) .
4.函数 \(f(x)=\ln x-\dfrac{1}{x-1}\)的零点的个数是\(\underline{\quad \quad}\).
参考答案
- 答案 （1）\(－3\) （2）\(3\)
解析 (1)令\(\dfrac{x+3}{x}=0\)，解得\(x＝－3\)．故函数 \(f(x)=\dfrac{x+3}{x}\)的零点是\(－3\)；
(2)令\(1-\log_3 x＝0\)，即\(\log_3 x＝1\)，解得\(x＝3\)．
故函数\(f(x)＝1-\log_3 x\)的零点是\(3\)． - 答案 \(D\)
解析 对于\(A\)，\(y=x^2\)的对称轴为\(y\)轴，故\(y=x^2\)是偶函数，
令\(x^2=0\)得\(x=0\)，所以\(y=x^2\)的零点为\(x=0\)．不符合题意．
对于\(B\)， \(y=\sqrt{x}\)的定义域为\([0，+∞)\)，不关于原点对称，
故 \(y=\sqrt{x}\)不是偶函数，不符合题意．
对于\(C\)，\(y=\log_2x\)的定义域为\((0，+∞)\)，不关于原点对称，
故\(y=\log_2x\)不是偶函数，不符合题意．
对于\(D\)， \(-\left(\dfrac{1}{2}\right)^{|-x|}=-\left(\dfrac{1}{2}\right)^{|x|}\) ，故 \(y=-\left(\dfrac{1}{2}\right)^{|x|}\)是偶函数，
令 \(-\left(\dfrac{1}{2}\right)^{|x|}=0\)，方程无解．即 \(y=-\left(\dfrac{1}{2}\right)^{|x|}\) 无零点．
故选：\(D\)． - 答案 \(2\)
解析 因为函数 \(f(x)=\left\{\begin{array}{l} |\ln x|, \quad x>0 \\ -2 x(x+2), \quad x \leq 0 \end{array}\right.\)，
且\(x≤0\)时\(f(x)=－2x(x+2)=－2(x+1)^2+2\)；
所以\(f(x)\)的图象如图，
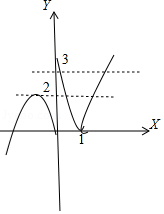
由图可得：\(y=f(x)\)与\(y=3\)只有两个交点；即函数\(y=f(x)－3\)的零点个数是\(2\).
- 答案 \(2\)
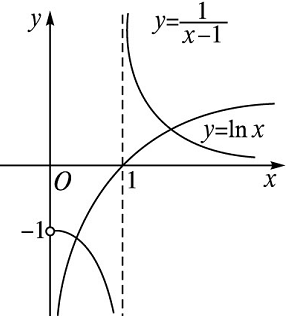
解析 在同一坐标系中画出函数\(y=\ln x\)与 \(y=\dfrac{1}{x-1}\)的图象如图所示，
因为函数\(y=\ln x\)与 \(y=\dfrac{1}{x-1}\)的图象有两个交点，
所以函数 \(f(x)=\ln x-\dfrac{1}{x-1}\)的零点个数为2．
【题型2】函数零点存在定理的应用
【典题1】 函数\(f(x)=\ln x+2x-6\)的零点所在的区间为( )
A．\((1，2)\) \(\qquad \qquad\) B．\((2，3)\) \(\qquad \qquad\) C．\((3，4)\) \(\qquad \qquad\) D．\((4，5)\)
解析 \(f(1)=2-6=-4<0\)，\(f(2)=4+\ln2-6=\ln2-2<0\)，
\(f(3)=6+\ln3-=\ln3>0\)，\(f(4)=8+\ln4-6=\ln4+2>0\)，
\(∴f(2)f(3)<0\)，\(∴m\)的所在区间为\((2，3)\)．
故选：\(B\)．
点拨 利用函数零点存在定理求解，主要是判断函数值的正负.
【典题2】 已知关于\(x\)的方程\(x^2-2mx+m-3=0\)的两个实数根\(x_1\)，\(x_2\)满足\(x_1∈(-1,0)\)，\(x_2∈(3,+∞)\)，则实数\(m\)的取值范围是\(\underline{\quad \quad}\) .
解析 \(∵\)程\(x^2-2mx+m-3=0\)的两个实数根\(x_1\)，\(x_2\)可看作函数\(f(x)=x^2-2mx+m-3\)的零点，
\(∴\)方程的根满足\(x_1∈(-1，0)\)，\(x_2∈(3，+∞)\)，
即函数\(f(x)\)的零点满足\(x_1∈(-1,0)\)，\(x_2∈(3,+∞)\)，
根据零点判定定理得， \(\left\{\begin{array}{l}
f(-1)>0 \\
f(0)<0 \\
f(3)<0
\end{array}\right.\)，即 \(\left\{\begin{array}{l}
1+2 m+m-3>0 \\
m-3<0 \\
9-6 m+m-3<0
\end{array}\right.\)，
化简得 \(\left\{\begin{array}{l}
m>\dfrac{2}{3} \\
m<3 \\
m>\dfrac{6}{5}
\end{array}\right.\)，解得 \(\dfrac{6}{5}<m<3\)，
\(∴\)实数\(a\)的取值范围是 \(\left(\dfrac{6}{5}, 3\right)\)．
点拨 这是二次函数零点的分布问题，主要是结合函数图象利用函数的零点存在定理求解.
巩固练习
1.若函数\(f(x)\)的图象是连续的，且函数\(f(x)\)的唯一零点同时在区间\((1,5)\)，\((1,3)\)，\((2,3)\)， \(\left(2, \dfrac{5}{2}\right)\)内，则与\(f(1)\)符号相同的是( )
A．\(f(5)\) \(\qquad \qquad\) B．\(f(3)\) \(\qquad \qquad\) C． \(f\left(\dfrac{5}{2}\right)\) \(\qquad \qquad\) D．\(f(2)\)
2.[多选]函数\(f(x)=x^3+3x-2\)的一个正零点所在的区间不可能是( )
A．\((3，4)\) \(\qquad \qquad\) B．\((2，3)\) \(\qquad \qquad\)C．\((1，2)\) \(\qquad \qquad\) D．\((0，1)\)
3.若函数 \(f(x)=\ln (x+1)-\dfrac{2}{x}\)的零点在区间\((k，k+1)(k∈z)\)上，则\(k\)的值为( )
A．\(－1\) \(\qquad \qquad\) B．\(1\) \(\qquad \qquad\) C．\(-1\)或\(2\)\(\qquad \qquad\) D．\(－1\)或\(1\)
4.已知\(a\)是实数，函数\(f(x)=x^2-ax+1\)在区间\((0，1)\)与\((1，2)\)上各有一个零点，则\(a\)的取值范围是\(\underline{\quad \quad}\)．
参考答案
- 答案 \(D\)
解析 因为函数\(f(x)\)有唯一零点，且根据题意可知函数的零点在 \(\left(2, \dfrac{5}{2}\right)\)上，
又因为零点左侧的函数值同号，零点右侧的函数值同号，
所以与\(f(1)\)符号相同的只能是\(f(2)\)，故选：\(D\)． - 答案 \(ABC\)
解析 函数\(f(x)=x^3+3x-2\)，把\(x=0，1，2，3，4\)代入，
若\(f(a)\cdot f(b)<0\)，
则零点在\((a，b)\)，\(f(0)=-2<0\)，\(f(1)=2>0\)，\(f(2)=12>0\)，\(f(3)=34>0\)，\(f(4)=76>0\)，
所以\(f(0)<0，f(1)>0\)，
所以函数的零点在\((0，1)\)，
故选：\(ABC\)． - 答案 \(D\)
解析 \(∵f(1)=\ln2-2<0\)，\(f(2)=\ln3-1>0\)，\(∴f(1)f(2)<0\)，
\(∴\)函数的零点在\((1，2)\)之间，
\(∵\)函数 \(f(x)=\ln (x+1)-\dfrac{2}{x}\)的零点在区间\((k，k+1)(k∈z)\)上，\(∴k=1\)，
又 \(y=\ln (x+1)\)与 \(y=\dfrac{2}{x}\)在\((-1，0)\)有交点，\(∴k=-1\)
\(∴k\)的值为\(－1\)或\(1\)．故选\(D\)． - 答案 \(\left(2, \dfrac{5}{2}\right)\)
解析 \(∵\)函数\(f(x)=x^2-ax+1\)在区间\((0，1)\)与\((1，2)\)上各有一个零点，
\(\therefore\left\{\begin{array}{l} f(0)=1>0 \\ f(1)=2-a<0 \\ f(2)=5-2 a>0 \end{array}\right.\)，解得 \(2<a<\dfrac{5}{2}\)．
故答案为 \(2<a<\dfrac{5}{2}\)．
分层练习
【A组---基础题】
1.设函数\(f(x)=e^x+\ln x\)，满足\(f(a)f(b)f(c)<0(a<b<c)\)，若\(f(x)\)存在零点\(x_0\)，则下列选项中一定错误的是( )
A．\(x_0∈(a，c)\) \(\qquad \qquad\) B．\(x_0∈(a，b)\) \(\qquad \qquad\) C．\(x_0∈(b，c)\) \(\qquad \qquad\) D．\(x_0∈(c，+∞)\)
2.下列函数既是偶函数又有零点的是( )
A．\(y=x^2+1\) \(\qquad \qquad\) B．\(y=2^{|x|}\) \(\qquad \qquad\) C．\(y=x^2+x\) \(\qquad \qquad\) D．\(y=1+lg|x|\)
3.下列函数中，在\((－1,1)\)内有零点且单调递增的是( )
A． \(y=\log _{\dfrac{1}{3}} x\) \(\qquad \qquad\) B．\(y=3^x-1\) \(\qquad \qquad\) C． \(y=x^{2}-\dfrac{1}{2}\) \(\qquad \qquad\) D．\(y=－x^3\)
4.[多选]已知函数\(f(x)=\dfrac{1}{x}+\dfrac{1}{2} x^{2}-2\)，利用零点存在性法则确定各零点所在的范围．下列区间中存在零点的是( )
A．\((－3,－2)\) \(\qquad \qquad\) B． \(\left(\dfrac{1}{2}, 1\right)\) \(\qquad \qquad\) C．\((2,3)\) \(\qquad \qquad\) D． \(\left(-1, \dfrac{1}{2}\right)\)
5.方程\(2^x+x-2=0\)的解所在的区间为( )
A．\((-1,0)\) \(\qquad \qquad\) B．\((0,1)\) \(\qquad \qquad\) C．\((1,2)\) \(\qquad \qquad\) D．\((2,3)\)
6.已知函数\(f(x)=\log_2x+x-b\)的零点在区间\([0,1]\)上，则\(b\)的取值范围为\(\underline{\quad \quad}\)．
7.函数\(f(x)=|x+2|－2^x\)在定义域内零点的个数是\(\underline{\quad \quad}\)．
8.若函数\(f(x)=x^2+tx+1\)在区间\((1，2)\)上有一个零点，则实数\(t\)的取值范围是\(\underline{\quad \quad}\)．
参考答案
-
答案 \(C\)
解析 函数 \(f(x)=e^x+\ln x\)的定义域为\(\{x|x>0\}\)，函数是增函数，
满足\(f(a)f(b)f(c)<0(a<b<c)\)，说明\(f(a)\)，\(f(b)\)，\(f(c)\)，有\(1\)个是负数一定是\(f(a)\)两个正数或\(3\)个负数，
由函数的零点判断定理可知，函数的零点在\((a,c)\)，在\((a,b)\)，在\((c,+∞)\)，不可能在\((b,c)\)．
故选：\(C\)． -
答案 \(D\)
解析 由偶函数定义再定义内满足\(f(-x)=f(x)\)，是偶函数的是\(A，B，D\)；
且\(A，B\)没有零点；\(D\)有零点 \(x=\dfrac{1}{e}\)，故选：\(D\)． -
答案 \(B\)
解析 根据题意，依次分析选项：
对于\(A\)， \(y=\log _{\frac{1}{3}} x\)，其定义域为\((0,+∞)\)，在\((－1,0)\)上没有定义，不符合题意；
对于\(B\)，\(y=3^x－1\)，在\((－1,1)\)上有零点\(x=0\)，且在\((－1,1)\)为增函数，符合题意；
对于\(C\)， \(y=x^{2}-\dfrac{1}{2}\)，为二次函数，在\((－1,0)\)上为减函数，不符合题意；
对于\(D\)，\(y=-x^3\)，在\((-1,1)\)上为减函数，不符合题意；
故选：\(B\)． -
答案 \(ABD\)
解析 经计算 \(f(-3)=-\dfrac{1}{3}+\dfrac{9}{2}-2=\dfrac{13}{6}>0\)， \(f(-2)=-\dfrac{1}{2}+2-2=-\dfrac{1}{2}<0\)，
\(f\left(\dfrac{1}{2}\right)=2+\dfrac{1}{8}-2=\dfrac{1}{8}>0\)， \(f(1)=1+\dfrac{1}{2}-2=-\dfrac{1}{2}<0\)， \(f(-1)=-1+\dfrac{1}{2}-2=-\dfrac{5}{2}<0\)，
根据零点判定定理可得区间\((-3,-2)\)， \(\left(\dfrac{1}{2}, 1\right)\)， \(\left(-1, \dfrac{1}{2}\right)\)上存在零点，
故选：\(ABD\)． -
答案 \(B\)
解析 令\(f(x)=2^x+x-2\)，由于\(f(0)=-2<0，f(1)=1>0\)，
\(∴f(0)f(1)<0\)，根据函数零点的判定定理可得\(f(x)\)的零点所在的区间为\((0，1)\)，
故方程\(2^x+x-2=0\)的解所在的区间为\((0，1)\)，
故选：\(B\)． -
答案 \((-∞,1]\)
解析 因为函数\(f(x)=\log_2x+x-b\)的零点在区间\((0,1]\)上是单调递增，
函数\(f(x)=\log_2x+x-b\)的零点在区间\((0,1]\)上，\(x→0\)，\(\log_2x+x→-∞\)，\(f(x)<0\)，可得\(b∈R\)
所以\(f(1)=\log_21+1-b≥0\)，解得\(b≤1\)． -
答案 \(3\)
解析 在同一坐标系中画出函数\(y=|x+2|\)与\(y=2^x\)的图象，
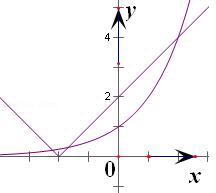
可以看到\(2\)个函数的图象在第二象限有\(2\)个交点，在第一象限有\(1\)个交点，
所以函数 \(f(x)=|x+2|－2^x\)在定义域内有\(3\)个零点． -
答案 \(\left(-\dfrac{5}{2},-2\right)\)
解析 函数\(f(x)=x^2+tx+1\)在区间\((1，2)\)上有一个零点，
若方程\(f(x)=x^2+tx+1=0\)的判别式为\(△=t^2-4=0\)，可得\(t=2\)或\(－2\)，
当\(t=2\)时，\(f(x)=x^2+2x+1=0\)，有零点\(x=-1\)，不满足题意；
当\(t=-2\)时，\(f(x)=x^2-2x+1=0\)，有零点\(x=1\)，不满足题意；
若\(△>0\)可得\(△=t^2-4>0\)，可得\(t>2\)或\(t<－2\)，
\(∴f(1)f(2)<0\)，
可得\((t+2)(5+2t)<0\)，解得 \(-\dfrac{5}{2}<t<-2\)，
综上 \(-\dfrac{5}{2}<t<-2\).
【B组---提高题】
1.已知实数\(x_0\)是函数 \(f(x)=\sqrt{x}-\dfrac{6}{x}\)的一个零点，若\(0<x_1<x_0<x_2\)，则( )
A．\(f(x_1)<0，f(x_2)<0\) \(\qquad \qquad\) B．\(f(x_1)<0，f(x_2)>0\)
C．\(f(x_1)>0，f(x_2)<0\) \(\qquad \qquad\) D．\(f(x_1)>0，f(x_2)>0\)
2.若方程\(2ax^2-x-1=0\)在\((0，1)\)内恰有一个零点，则有( )
A．\(a<-1\) \(\qquad \qquad\) B．\(a>1\) \(\qquad \qquad\) C．\(－1<a<1\) \(\qquad \qquad\) D．\(0≤a<1\)
3.方程 \(3^x+4^x=5^x\)解的情况是( )
A.有且只有一个根\(2\) \(\qquad \qquad\) B.不仅有根\(2\)还有其他根
C.有根\(2\)和另一个负根 \(\qquad \qquad\) D.有根\(2\)和另一个正根
4.设函数 \(f(x)=|\ln x|-\dfrac{1}{x+1}\)的两个零点为\(x_1，x_2\)，则有( )
A．\(x_1 x_2<1\) \(\qquad \qquad\) B．\(x_1 x_2=1\) \(\qquad \qquad\) C． \(1<x_{1} x_{2}<\sqrt{2}\) \(\qquad \qquad\) D． \(x_{1} x_{2} \geq \sqrt{2}\)
5.已知函数\(f(x)=3^x+x\)，\(g(x)=x^3+x\)，\(h(x)=\log_3x+x\)的零点依次为\(a，b，c\)，则( )
A．\(c<b<a\) \(\qquad \qquad\) B．\(a<b<c\) \(\qquad \qquad\) C．\(c<a<b\) \(\qquad \qquad\) D．\(b<a<c\)
6.若方程\(2-x^2=|x-a|\)至少有一个负数解，则实数\(a\)的取值范围\(\underline{\quad \quad}\)．
7.已知函数\(y=f(x)\)有\(9\)个零点\(x_1,x_2,…,x_9\)，且函数\(y=f(x)\)满足\(f(3+x)=f(3-x)\)，则\(x_1+x_2+⋯+x_9=\)\(\underline{\quad \quad}\)．
8.已知\(x_1 、x_2\)是函数 \(f(x)=|\ln x|-e^{-x}\)的两个零点，则\(x_1 x_2\)所在区间是\(\underline{\quad \quad}\)．
参考答案
-
答案 \(B\)
解析 函数 \(f(x)=\sqrt{x}-\dfrac{6}{x}\)在\((0，+∞)\)上递增，且\(f(x_0 )=0\)，由图象可知，
当\(0<x_1<x_0<x_2\)时，有\(f(x_1 )<0\)，\(f(x_2 )>0\)，故选：\(B\)． -
答案 \(B\)
解析 \(∵\)方程\(2ax^2-x-1=0\)在\((0，1)\)内恰有一个零点，
\(f(0)=-1\)，\(f(1)=2a-1-1=2a-2\)，
\(∴f(1)=2a-2>0\)，解得\(a>1\)．故选：\(B\)． -
答案 \(A\)
解析 方程 \(3^x+4^x=5^x\)等价为 \(\left(\dfrac{3}{5}\right)^{x}+\left(\dfrac{4}{5}\right)^{x}=1\)
设 \(f(x)=\left(\dfrac{3}{5}\right)^{x}+\left(\dfrac{4}{5}\right)^{x}\)，
则函数\(f(x)\)在\(R\)上为减函数，
\(\because f(2)=\left(\dfrac{3}{5}\right)^{2}+\left(\dfrac{4}{5}\right)^{2}=1\)
\(∴\)方程 \(3^x+4^x=5^x\)有且只有一个根\(2\)，故选\(A\). -
答案 \(A\)
解析 由 \(f(x)=|\ln x|-\dfrac{1}{x+1}\)，得 \(|\ln x|=\dfrac{1}{x+1}\)，
作函数 \(y=|\ln x|\)与 \(y=\dfrac{1}{x+1}\)的图象如图，
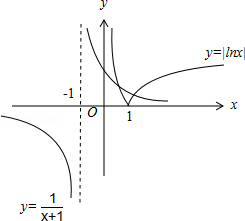
不妨设\(x_1<x_2\)，由图可知，\(x_1<1<x_2\)，则 \(\ln x_{1}<0\)，且 \(\left|\ln x_{1}\right|>\left|\ln x_{2}\right|\)，
\(∴-\lnx_1>\lnx_2\)，则\(\ln x_1+\ln x_2<0\)，即\(\ln x_1 x_2<0\)，
\(∴x_1 x_2<1\)．故选：\(A\)． -
答案 \(B\)
解析 (1)令 \(f(x)=3^x+x=0\)，即 \(3^x+x=0\)，化为\(3^x=-x\)，
分别作出函数\(y=3^x，y=-x\)的图象，
由图象可以知道函数\(f(x)\)的零点\(a<0\)，
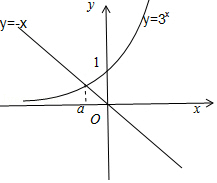
(2)对于函数 \(g(x)=x^3+x=x(x^2+1)\)，令\(g(x)=0\)，则\(x=0\)，
\(∴b=0\)；
(3)令\(h(x)=\log_3x+x=0\)，则\(\log_3x+x=0\)，即\(\log_3x=-x\)，
分别作出函数\(y=\log_3x，y=－x\)的图象，
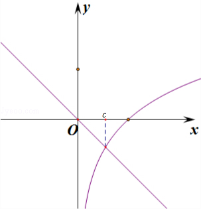
则\(c>0\)，
综上可知：\(a<b<c\)，故选\(B\)． -
答案 \(\left(-\dfrac{9}{4}, 2\right)\)
解析 由题意，\(2-x^2≥0\)，解得 \(-\sqrt{2} \leq x \leq \sqrt{2}\)；
若方程\(2-x^2=|x-a|\)至少有一个负数解，
①当\(a≤0\)时，\(x-a=2-x^2\)，\(-x+a=2-x^2\)在 \([-\sqrt{2}, 0)\)上有解，
故 \(-\dfrac{9}{4}<a \leq 0\)；
②当\(a>0\)时，则\(x-a=-(2-x^2 )\)成立，
即 \(a=-x^{2}+x+2=-\left(x-\dfrac{1}{2}\right)^{2}+\dfrac{9}{4}\)；
\(\because-\sqrt{2} \leq x<0\)；\(∴0<a<2\)；
故实数\(a\)的取值范围为 \(\left(-\dfrac{9}{4}, 2\right)\). -
答案 \(27\)
解析 \(∵\)函数\(y=f(x)\)满足\(f(3+x)=f(3-x)\)，
即函数\(y=f(x)\)的图象关于直线\(x=3\)对称
即函数\(y=f(x)\)的零点关于直线x\(=3\)对称
不妨令\(x_1<x_2<⋯<x_9\)，则
即 \(\dfrac{1}{2}\left(x_{1}+x_{9}\right)=3, \dfrac{1}{2}\left(x_{2}+x_{8}\right)=3, \dfrac{1}{2}\left(x_{3}+x_{7}\right)=3\)，\(\dfrac{1}{2}\left(x_{4}+x_{6}\right)=3, \dfrac{1}{2}\left(x_{5}+x_{5}\right)=3\),
\(∴x_1+x_2+⋯+x_9=3×9=27\). -
答案 \(\left(\dfrac{1}{e}, 1\right)\)
解析 令\(f(x)=0\)， \(\therefore|\ln x|=e^{-x}\)；
\(∴\)函数\(f(x)\)的零点便是上面方程的解，即是函数\(y=|\ln x|\)和函数 \(y=e^{-x}\)的交点，
画出这两个函数图象如下：
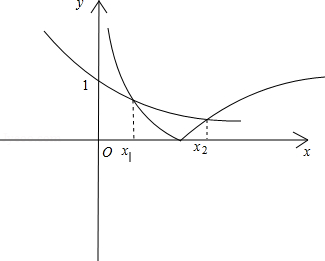
由图看出\(0<-\ln x_1<1\)，\(-1<\ln x_1<0\),\(0<\ln x_2<1\)；
\(∴-1<\ln x_1+\ln x_2<1\)；\(∴-1<\ln x_1 x_2<1\)；
\(\therefore \dfrac{1}{e}<x_{1} x_{2}<e\)；
由图还可看出，\(-\ln x_1>\ln x_2\)；\(∴\ln x_1 x_2<0\)，\(x_1 x_2<1\)；
\(∴x_1 x_2\)的范围是 \(\left(\dfrac{1}{e}, 1\right)\)．
【C组---拓展题】
1.已知函数 \(f(x)=\left\{\begin{array}{l}
\left|\log _{2} x\right|, \quad x>0 \\
x^{2}+4 x+1, \quad x \leq 0
\end{array}\right.\)，若函数\(F(x)=f(x)－b\)有四个不同的零点\(x_1，x_2，x_3，x_4\)\((x_1<x_2<x_3<x_4)\)，则 \(\dfrac{x_{4}}{x_{3}}-\dfrac{x_{1} x_{3}^{2}+x_{2} x_{3}^{2}}{4}\)的取值范围是\(\underline{\quad \quad}\) .
2.已知函数 \(f(x)=\left\{\begin{array}{l}
-x^{2}-4 x+1, x \leq 0 \\
2-2^{-x}, x>0
\end{array}\right.\)若关于\(x\)的方程\(2f^2 (x)－(2m+1)f(x)+m=0\)恰有\(3\)个不同的实根，则\(m\)的取值范围为\(\underline{\quad \quad}\) .
3.已知\(a，b，c∈N^*\)，方程\(ax^2+bx+c=0\)在区间\((-1，0)\)上有两个不同的实根，求\(a+b+c\)的最小值．
参考答案
-
答案 \(\left(2, \dfrac{17}{4}\right]\)
解析 作出\(f(x)\)的函数图象如图所示：
由图象知 \(x_1+x_2=－4\)，\(x_3 x_4=1\)，\(0<b≤1\)，
解不等式\(0<－\log_2x≤1\)得： \(\dfrac{1}{2} \leq x_{3}<1\)，
\(\therefore \dfrac{x_{4}}{x_{3}}-\dfrac{x_{1} x_{3}^{2}+x_{2} x_{3}^{2}}{4}=\dfrac{1}{x_{3}{ }^{2}}+x_{3}{ }^{2}\)，
令\(t=x_3^2\)，则 \(\dfrac{1}{4} \leq t<1\)，
令 \(g(t)=t+\dfrac{1}{t}\)，则\(g(t)\)在 \(\left[\dfrac{1}{4}, 1\right]\)上单调递减，\(g(1)=2\)， \(g\left(\dfrac{1}{4}\right)=\dfrac{17}{4}\)，
\(\therefore g(1)<g(t) \leq g\left(\dfrac{1}{4}\right)\)，即 \(2<t+\dfrac{1}{t} \leq \dfrac{17}{4}\). -
答案 \([2,5)∪\{1\}\)
解析 由\(2f^2 (x)-(2m+1)f(x)+m=[2f(x)-1][f(x)-m]=0\) ，
得 \(f(x)=\dfrac{1}{2}\)或\(f(x)=m\)，
作出\(y=f(x)\)的图象，如图所示，
由图可知，方程 \(f(x)=\dfrac{1}{2}\)有\(1\)个实根，故方程\(f(x)=m\)有\(2\)个实根，
故\(m\)的取值范围为\([2,5)∪\{1\}\)．
-
答案 \(11\)
解析 设\(x_1\)和\(x_2\)方程 \(ax^2+bx+c=0\)有两个相异根，由 \(a，b，c∈N^*\)，
两个根都在区间\((-1，0)\)上，
可得函数\(f(x)=ax^2+bx+c\)在区间\((-1，0)\)上与\(x\)轴有两个不同的交点，
故有\(f(－1)=a+c-b>0\)，且\(f(0)=c>0\)，且\(△=b^2-4ac>0\)，
且 \(x_{1}+x_{2}=-\dfrac{b}{a} \in(-2,0)\)，且 \(x_{1} \cdot x_{2}=\dfrac{c}{a} \in(0,1)\)．
故\(c\)的最小值为\(1\)，故有 \(\left\{\begin{array}{l} a+1>b \\ a>c=1 \\ b^{2}>4 a \end{array}\right.\)．
当\(a=2\)时，正整数\(b\)不存在；当\(a=3\)时，正整数\(b\)不存在；
当\(a=4\)时，正整数\(b\)不存在；当\(a=5\)时，存在正整数\(b=5\)．
综上可得，\(c\)的最小值为\(1\)，\(a\)的最小值为\(5\)，\(b\)的最小值为\(5\)，
故\(a+b+c\)的最小值为\(1+5+5=11\)．
浙公网安备 33010602011771号