4.2 指数函数

${\color {Red}{欢迎到学科网下载资料学习 }}$
【基础过关系列】2022-2023 学年高一数学上学期同步知识点剖析精品讲义 (人教 A 版 2019）
${\color {Red}{ 跟贵哥学数学，so \quad easy！}}$

必修第一册同步巩固，难度 2 颗星！

基础知识

指数函数概念

一般地，函数 $y=a^x (a>0$ 且 $a≠1)$ 叫做指数函数，其中 $x$ 是自变量，函数的定义域为 $R$.
解释
(1) 指数函数 $y=a^x (a>0$ 且 $a≠1)$ 中系数为 $1$，底数是不为 $1$ 的正实数的常数，指数是变量 $x$. 注意与幂函数的区别，如 $y=2^x$ 是指数函数，$y=x^3$ 是幂函数.
(2) 指数函数中为什么要限制 $a>0$ 且 $a≠1$ 呢？
① 若 $a<0$，则对于 $x$ 的某些值 $a^x$ 无意义，如 $(-2)^x$，此时 $x$ 取 $\dfrac{1}{2}, \dfrac{1}{4}$… 等没意义；其函数图象没明显特点；
② 若 $a=0$ 或 $a=1$ 时，函数没研究价值.
 

指数函数的图像与性质

函数名称	指数函数
定义	函数$y=a^x (a>0$且$a≠1)$叫做指数函数
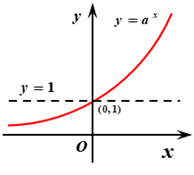
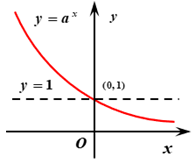
图象	$a>1$	$0< a <1$
定义域	$R$
值域	$(0,+∞)$
过定点	图象过定点$(0,1)$，即当$x=0$时，$y=1$
奇偶性	非奇非偶
单调性	在$R$上是增函数	在$R$上是减函数
$a$变化对图象的影响	在第一象限内，$a$越大图象越高；在第二象限内，$a$越大图象越低

 

【例】画出函数 $y=2^x$ 和 $y=\left(\dfrac{1}{2}\right)^{x}$ 的图象，说下他们的函数性质.
解析

$y=2^x$：在 $R$ 上递增，非奇非偶函数，值域是 $(0,+∞)$;
$y=\left(\dfrac{1}{2}\right)^{x}$：在 $R$ 上递减，非奇非偶函数，值域是 $(0,+∞)$.
$y=2^x$ 与 $y=\left(\dfrac{1}{2}\right)^{x}$ 关于 $y$ 轴对称.
 

指数型函数模型

形如 $y=k·a^x (k∈R，$ 且 $k≠0；a>0，$ 且 $a≠1)$ 的函数称为指数型函数．
 

基本方法

【题型1】指数函数的概念

【典题 1】已知指数函数 $f(x)$ 的图象经过点 $\left(-2, \dfrac{1}{16}\right)$，试求 $f(-1)$ 和 $f(3)$．
解析 设 $f(x)=a^x (a>0,$ 且 $a≠1)$，
$∵$ 函数 $f(x)$ 的图象经过点 $\left(-2, \dfrac{1}{16}\right)$，
$\therefore a^{-2}=\dfrac{1}{16}$，解得 $a=±4$．
又 $a>0$，则 $a=4$，$∴f(x)=4^x$，
$\therefore f(-1)=4^{-1}=\dfrac{1}{4}$，$f(3)=4^3=64$.
点拨 待定系数法求解函数解析式.
 

巩固练习

1. 下列函数中是指数函数的是 $\underline{\quad \quad}$ (填序号)．
 ① $y=2 \cdot(\sqrt{2})^{x}$；② $y=2^{x-1}$；③ $y=\left(\dfrac{\pi}{2}\right)^{x}$；④$y=x^x$；⑤ $y=3^{-\frac{1}{x}}$；⑥ $y=x^{\frac{1}{3}}$．
 

2. 若指数函数 $f(x)$ 的图象经过点 $(2,9)$，求 $f(x)$．
 
 

参考答案

1. 答案 ③
   解析 ① $y=2 \cdot(\sqrt{2})^{x}$ 的系数不是 $1$，不是指数函数；
   ② $y=2^{x-1}$ 的指数不是自变量 $x$，不是指数函数；
   ③ $y=\left(\dfrac{\pi}{2}\right)^{x}$ 是指数函数；
   ④ $y=x^x$ 的底数是 $x$ 不是常数，不是指数函数；
   ⑤ $y=3^{-\dfrac{1}{x}}$ 的指数不是自变量 $x$，不是指数函数；
   ⑥ $y=x^{\dfrac{1}{3}}$ 是幂函数.
   故答案：③

2. 答案 $f(x)=3^x$
   解析 设 $f(x)=ax(a>0,$ 且 $a≠1)$，
   因为函数 $f(x)$ 的图象经过点 $(2,9)$，代入可得 $a^2=9$，解得 $a=3$ 或 $a=-3$(舍去)．
   故 $f(x)=3^x$．
    

【题型2】指数函数的图象与性质

【典题 1】 如图是指数函数①$y=a^x$，②$y=b^x$，③$y=c^x$，④$y=d^x$ 的图象，则 $a,b,c,d$ 与 $1$ 的大小关系是 (　　)

 A．$a<b<1<c<d$ $\qquad \qquad$ B．$b<a<1<d<c$$\qquad \qquad$
 C．$1<a<b<c<d$ $\qquad \qquad$ D．$a<b<1<d<c$
解析 设 $x=1$ 与①②③④的图象分别交于点 $A,B,C,D$，如图，则其坐标依次为 $(1,a)，(1,b)，(1,c)，(1,d)$，由图象观察可得 $c>d>1>a>b$．故选 $B$．
 

【典题 2】 函数 $y=|2^x-1|$ 的大致图象是 (　　)
 A． $\qquad \qquad$ B．
 C． $\qquad \qquad$ D．
解析 $y=\left|2^{x}-1\right|=\left\{\begin{array}{l} 2^{x}-1, x \geq 0 \\ -2^{x}+1, x<0 \end{array}\right.$，
当 $x<0$ 时，$y=1－2^x$ 的图象是将 $y=2^x$ 图象先沿 $x$ 轴对称下来，再沿 $y$ 轴向上平移 $1$ 个单位，
此时 $x<0$ 时的图象在 $x$ 轴上方，且为增函数，渐近线为 $y=1$，
只有 $C$ 项满足题意．故选 $C$.
点拨 含绝对值的函数可利用 $|a|=\left\{\begin{array}{cc} a, & a \geq 0 \\ -a, & a<0 \end{array}\right.$ 转化为分段函数，也可以函数图象的变换画出其函数图象.
 

巩固练习

1. 如图是指数函数①$y=a^x$ ②$y=b^x$ ③$y=c^x$ ④$y=d^x$ 的图象，则 $a,b,c,d$ 与 $1$ 的大小关系是 (　　)

 A．$c<d<1<a<b$ $\qquad \qquad$ B．$d<c<1<b<a$ $\qquad \qquad$ C．$c<d<1<b$ $\qquad \qquad$ D．$1<c<d<a<b$
 

2. 如果 $a>1,b<-1$，那么函数 $f(x)=a^x+b$ 的图象在 (　　)
 A．第一、二、三象限 $\qquad \qquad$ B．第一、三、四象限 $\qquad \qquad$ C．第二、三、四象限 $\qquad \qquad$ D．第一、二、四象限
 

3. 函数 $y=e^{-|x|}$($e$ 是自然底数) 的大致图象是 (　　)
A． $\qquad \qquad$ B． $\qquad \qquad$ C． $\qquad \qquad$ D．
 

参考答案

1. 答案 $B$
   解析 $∵$ 当底数大于 $1$ 时指数函数是定义域内的增函数，当底数大于 $0$ 小于 $1$ 时是定义域内的减函数，
   可知 $a，b$ 大于 $1$，$c，d$ 大于 $0$ 小于 $1$．
   又由图可知 $a^1>b^1$，即 $a>b$．$d^1<c^1$，即 $d<c$．
   $∴a,b,c,d$ 与 $1$ 的大小关系是 $d<c<1<b<a$．
   故选：$B$．

2. 答案 $B$
   解析 $∵a>1$，$∴y=a^x$ 的图象过第一、第二象限，且是单调增函数，经过 $(0,1)$，
   $f(x)=a^x+b$ 的图象可看成把 $y=a^x$ 的图象向下平移 $－b(－b>1)$ 个单位得到的，
   故函数 $f(x)=a^x+b$ 的图象，经过第一、第三、第四象限，不经过第二象限，
   故选：$B$．

3. 答案 $C$
   解析 $\because y=e^{-|x|}=\left\{\begin{array}{l} \left(\dfrac{1}{e}\right)^{x}, x \geq 0 \\ e^{x}, x<0 \end{array}\right.$．根据指数函数的图象与性质可知：应选 $C$．
    

【题型3】指数函数的应用

角度1 比较指数式的大小

【典题 1】 设 $y_{1}=4^{0.9}, y_{2}=8^{0.48}, y_{3}=\left(\dfrac{1}{2}\right)^{-1.5}$，则 (　　)
 A．$y_3>y_1>y_2$ $\qquad \qquad$ B．$y_2>y_1>y_3$ $\qquad \qquad$ C．$y_1>y_2>y_3$ $\qquad \qquad$ D．$y_1>y_3>y_2$
解析 利用幂的运算性质可得，
$y_{1}=4^{0.9}=2^{1.8}$， $y_{2}=8^{0.48}=2^{1.44}$， $y_{3}=\left(\dfrac{1}{2}\right)^{-1.5}=2^{1.5}$，
再由 $y=2^x$ 是增函数，知 $y_1>y_3>y_2$．
故选：$D$．
点拨 注意数式的结构，通过构造函数，利用函数单调性比较大小.
 

巩固练习

1. 已知 $a=4^{\frac{1}{2}}, \quad b=2^{\frac{1}{3}}, \quad c=5^{\frac{1}{2}}$，则 $a、b、c$ 的大小关系为 (　　)
 A．$b<a<c$ $\qquad \qquad$ B．$a<b<c$ $\qquad \qquad$ C．$b<c<a$ $\qquad \qquad$ D．$c<a<b$
 

2. 已知 $a=0.7^{2.1}, \quad b=0.7^{2.5} . \quad c=2.1^{0.7}$，则这三个数的大小关系为 (　　)
 A．$b<a<c$ $\qquad \qquad$ B．$a<b<c$ $\qquad \qquad$ C．$c<a<b$ $\qquad \qquad$ D．$c<b<a$
 

参考答案

1. 答案 $A$
   解析 $a=4^{\frac{1}{2}}=2, \quad b=2^{\frac{1}{3}}<2, \quad c=5^{\frac{1}{2}}>2$，则 $c>a>b$，故选：$A$．
2. 答案 $A$
   解析 根据指数函数的性质可得：函数 $y=0.7^{x}$ 的底数小于 $1$，是减函数，
   $∵2.1<2.5$， $\therefore 0.7^{2.1}>0.7^{2.5}$，即 $a>b$．
   又 $\because c=2.1^{0.7}>2.1^{0}=1$， $a=0.7^{2.1}<0.7^{0}=1$，
   $∴c<a$，所以 $b<a<c$，故选：$A$．
    

角度2 求解指数型不等式

【典题 1】 已知集合 $N=\left\{x \mid \dfrac{1}{2}<2^{x+1}<4, x \in Z\right\}$，$M=\{-1,1\}$，则 $M∩N=\underline{\quad \quad}$.
解析 $\because \dfrac{1}{2}<2^{x+1}<4$， $\therefore 2^{-1}<2^{x+1}<2^{2}$，$∴-1<x+1<2⇒-2<x<1$，
$∴$ 集合 $N=\{x|-2<x<1,x∈z\}=\{-1,0\}$，
又 $∵M=\{-1,1\}$，$∴M∩N=\{-1\}$.
点拨 利用指数函数的单调性求解不等式.
 

巩固练习

1. 函数 $y=\sqrt{1-\left(\dfrac{1}{2}\right)^{x}}$ 的定义域是 $\underline{\quad \quad}$ .
 

2. 不等式 $3^{x^{2}+a x}>3^{2 x+a-2}$ 恒成立，则 $a$ 的取值范围是 $\underline{\quad \quad}$.
 

参考答案

1. 答案 $[0,+∞)$
   解析 由 $1-\left(\dfrac{1}{2}\right)^{x} \geq 0$ 得， $\left(\dfrac{1}{2}\right)^{x} \leq 1$，解得：$x≥0$，
   故函数 $y=\sqrt{1-\left(\dfrac{1}{2}\right)^{x}}$ 的定义域是 $[0,+∞).$

2. 答案 $(-2,2)$
   解析 不等式 $3^{x^{2}+a x}>3^{2 x+a-2}$ 恒成立，即 $x^2+ax>2x+a-2$，
   亦即 $x^2+(a-2)x-a+2>0$ 恒成立，
   则 $△=(a-2)^2-4(-a+2)<0$，解得 $-2<a<2$，
   故 $a$ 的取值范围是 $(-2,2)$．
    

角度3 指数型函数综合问题

【典题 1】如果函数 $y=a^2x+2a^x-1(a>0$ 且 $a≠1)$ 在区间 $[-1,1]$ 上有最大值 $14$，试求 $a$ 的值．
解析 设 $t=a^x$，则 $t>0$，原函数可化为 $y=(t+1)^2-2$，其图象的对称轴为 $t=-1$．
(1) 若 $a>1$，$∵x∈[-1,1]$， $\therefore t \in\left[\dfrac{1}{a}, a\right]$，
则函数 $y=(t+1)^2-2$ 在区间 $\left[\dfrac{1}{a}, a\right]$ 上单调递增，
$∴$ 当 $t=a$ 时，函数 $y$ 取得最大值 $(a+1)^2-2$，
即 $(a+1)^2-2=14$，解得 $a=3$ 或 $a=-5$(舍去)．
(1) 若 $0<a<1$，$∵x∈[－1,1]$， $\therefore \mathrm{t} \in\left[a, \dfrac{1}{a}\right]$，
则函数 $y=(t+1)^2-2$ 在区间 $\left[\dfrac{1}{a}, a\right]$ 上单调递增，
$∴$ 当 $t=\dfrac{1}{a}$ 时，函数 y 取得最大值 $\left(\dfrac{1}{a}+1\right)^{2}-2$，
即 $\left(\dfrac{1}{a}+1\right)^{2}-2=14$，解得 $a=\dfrac{1}{3}$ 或 $a=-\dfrac{1}{5}$(舍去)．
综上可知，$a$ 的值为 $3$ 或 $\dfrac{1}{3}$．
 

巩固练习

1. 已知函数 $f(x)=\left(\dfrac{1}{3}\right)^{a x^{2}-4 x+3}$，
  (1) 若 $a=-1$，求 $f(x)$ 的单调区间；
  (2) 若 $f(x)$ 有最大值 $3$，求 $a$ 的值．
  (3) 若 $f(x)$ 的值域是 $(0,+∞)$，求 $a$ 的取值范围．
 
 

参考答案

1. 答案 (1) 递增区间是 $(-2,+∞)$，递减区间是 $(-∞,-2 )$．(2) $1$ (3) $\{0\}$
   解析 (1) 当 $a=-1$ 时， $f(x)=\left(\dfrac{1}{3}\right)^{-x^{2}-4 x+3}$，
   令 $g(x)=-x^2-4x+3$，
   由于 $g(x)$ 在 $(-∞,-2)$ 上单调递增，在 $(-2,+∞)$ 上单调递减，
   而 $y=\left(\dfrac{1}{3}\right)^{t}$ 在 $R$ 上单调递减，
   所以 $f(x)$ 在 $(-∞,-2)$ 上单调递减，在 $(-2,+∞)$ 上 单调递增，
   即函数 $f(x)$ 的递增区间是 $(-2,+∞)$，递减区间是 $(-∞,-2 )$．
   (2) 令 $h(x)=ax^2-4x+3$， $y=\left(\dfrac{1}{3}\right)^{h(x)}$，由于 $f(x)$ 有最大值 $3$，
   所以 $h(x)$ 应有最小值 $-1$，
   因此 $\dfrac{12 a-16}{4 a}=-1$，解得 $a=1$．
   即当 $f(x)$ 有最大值 3 时，$a$ 的值等于 $1$．
   (3) 由指数函数的性质知，
   要使 $y=h(x)$ 的值域为 $(0,+∞)$．
   应使 $h(x)=ax^2-4x+3$ 的值域为 $R$，
   因此只能有 $a=0$．
   因为若 $a≠0$，则 $h(x)$ 为二次函数，其值域不可能为 $R$．
   故 $a$ 的取值范围是 $\{0\}$．
    

分层练习

【A组---基础题】

1. 函数 $y=(a-2)^2 a^x$ 是指数函数，则 (　　)
 A．$a=1$ 或 $a=3$ $\qquad \qquad$ B．$a=1$ $\qquad \qquad$ C．$a=3$ $\qquad \qquad$ D．$a>0$ 且 $a≠1$
 

2. 若函数 $y=a^x+b$ 的部分图象如图所示，则 (　　)

 A．$0<a<1,-1<b<0$ $\qquad \qquad$ B．$0<a<1,0<b<1$
 C．$a>1,-1<b<0$ $\qquad \qquad$ D．$a>1,0<b<1$
 

3. 函数 $y=\dfrac{x a^{x}}{|x|}(a>1)$ 的图象的大致形状是 (　　)
A． $\qquad \qquad$ B． $\qquad \qquad$ C． $\qquad \qquad$ D．
 

4. 已知 $a=1.6^{0.3}, b=1.6^{0.8}, c=0.7^{0.8}$，则 (　　)
 A．$c<a<b$ $\qquad \qquad$ B．$a<b<c$ $\qquad \qquad$ C．$b>c>a$ $\qquad \qquad$ D．$a>b>c$
 

5. 二次函数 $y=-x^2-4x(x>-2)$ 与指数函数 $y=\left(\dfrac{1}{2}\right)^{x}$ 的交点个数有 (　　)
 A．$3$ 个 $\qquad \qquad$ B．$2$ 个 $\qquad \qquad$ C．$1$ 个 $\qquad \qquad$ D．$0$ 个
 

6. 方程 $|2^x-1|=a$ 有唯一实数解，则 $a$ 的取值范围是 $\underline{\quad \quad}$．
 

7. 函数 $y=a^x-2(a>0$ 且 $a≠1，-1≤x≤1)$ 的值域是 $\left[-\dfrac{5}{3}, 1\right]$，则实数 $a=$$\underline{\quad \quad}$ .
 

8. 已知函数 $f(x)=\dfrac{1}{2^{x}-1}+\dfrac{1}{2}$．
  (1) 求 $f(x)$ 的定义域； (2) 讨论 $f(x)$ 的奇偶性．
 
 

9. 已知函数 $f(x)=b\cdot a^x$(其中 $a,b$ 为常量，且 $a>0,a≠1$) 的图象经过点 $A(1,6)$，$B(3,24)$．
  (1) 求 $f(x)$；
  (2) 若不等式 $\left(\dfrac{1}{a}\right)^{x}+\left(\dfrac{1}{b}\right)^{x}-m \geq 0$ 在 $x∈(-∞,1]$ 时恒成立，求实数 $m$ 的取值范围．
 
 

参考答案

1. 答案 $C$
   解析 由指数函数定义知 $\left\{\begin {array}{l} (a-2)^{2}=1 \\ a>0, \text { 且 } a \neq 1 \end {array}\right.$，所以解得 $a=3$．故选 $C$.

2. 答案 $A$
   解析 由图象可以看出，函数为减函数，故 $0<a<1$，
   因为函数 $y=a^x$ 的图象过定点 $(0,1)$，函数 $y=a^x+b$ 的图象过定点 $(0,b+1)$，
   $∴-1<b<0$，故选：$A$.

3. 答案 $C$
   解析 $f(x)$ 是分段函数，根据 $x$ 的正负写出分段函数的解析式，
   $f(x)=\left\{\begin{array}{l} a^{x}(x>0) \\ -a^{x}(x<0) \end{array}\right.$
   $∴x>0$ 时，图象与 $y=a^x$ 在第一象限的图象一样，
   $x<0$ 时，图象与 $y=a^x$ 的图象关于 $x$ 轴对称，
   故选：$C$．

4. 答案 $A$
   解析 $y=1.6^x$ 是增函数，故 $a=1.6^{0.3}<b=1.6^{0.8}$，而 $1.6^{0.3}>1>0.7^{0.8}$，故 $c<a<b$，故选：$A$．

5. 答案 $C$
   解析 因为二次函数 $y=-x^2-4x=-(x+2)^2+4(x>-2)$，
   且 $x=-1$ 时，$y=-x^2-4x=3$， $y=\left(\dfrac{1}{2}\right)^{x}=2$，
   则在坐标系中画出 $y=-x^2-4x(x>－2)$ 与 $y=\left(\dfrac{1}{2}\right)^{x}$ 的图象：
   由图可得，两个函数图象的交点个数是 $1$ 个，故选 $C$．
   

6. 答案 $a≥1$ 或 $a=0$
   解析 作出 $y=|2^x-1|$ 的图象，要使直线 $y=a$ 与图象的交点只有一个，$∴a≥1$ 或 $a=0$.
   

7. 答案 $3$ 或 $\dfrac{1}{3}$
   解析 当 $a>1$ 时，函数 $y=a^x-2(a>0$ 且 $a≠1)$，$-1≤x≤1$ 是增函数，
   $∵$ 值域是 $\left[a^{-1}-2, a-2\right]$， $\therefore\left\{\begin{array}{l} \dfrac{1}{a}-2=-\dfrac{5}{3} \\ a-2=1 \end{array} \Rightarrow a=3\right.$；
   当 $0<a<1$ 时，数 $y=a^x-2(a>0$ 且 $a≠1，-1≤x≤1)$ 是减函数，
   $∵$ 值域是 $\left[a-2, a^{-1}-2\right]$， $\therefore\left\{\begin{array}{l} \dfrac{1}{a}-2=1 \\ a-2=-\dfrac{5}{3} \end{array} \Rightarrow a=\dfrac{1}{3}\right.$．
   综上所述，可得实数 $a=3$ 或 $\dfrac{1}{3}$.

8. 答案 (1)$(-∞,0)∪(0,+∞)$ (2)$C$
   解析 (1) 由 $2x-1≠0$，得 $2x≠1$，即 $x≠0$，
   因此函数 $f(x)$ 的定义域为 $(-∞,0)∪(0,+∞)$．
   (2) 由 (1) 知，函数 $f(x)$ 的定义域为 $(-∞,0)∪(0,+∞)$，关于坐标原点对称，
   又 $f(-x)=\dfrac{1}{2^{-x}-1}+\dfrac{1}{2}=\dfrac{2 x}{1-2^{x}}+\dfrac{1}{2}=\dfrac{2^{x}-1+1}{1-2^{x}}+\dfrac{1}{2}$$=-1-\dfrac{1}{2^{x}-1}+\dfrac{1}{2}=-\left(\dfrac{1}{2^{x}-1}+\dfrac{1}{2}\right)=-f(x)$，
   所以 $f(x)$ 为奇函数．

9. 答案 (1) $f(x)=3\cdot 2^x$ (2) $\left[\dfrac{5}{6},+\infty\right)$
   解析 (1) 把 $A(1,6)$，$B(3,24)$ 代入 $f(x)=b\cdot a^x$，得 $\left\{\begin{array}{l} 6=a b \\ 24=b \cdot a^{3} \end{array}\right.$
   结合 $a>0$ 且 $a≠1$，解得 $\left\{\begin{array}{l} a=2 \\ b=3 \end{array}\right.$，
   $∴f(x)=3\cdot 2^x$．
   (2) 要使 $\left(\dfrac{1}{2}\right)^{x}+\left(\dfrac{1}{3}\right)^{x} \geq m$ 在 $(－∞,1]$ 上恒成立，
   只需保证函数 $y=\left(\dfrac{1}{2}\right)^{x}+\left(\dfrac{1}{3}\right)^{x}$ 在 $(－∞,1]$ 上的最小值不小于 $m$ 即可．
   $∵$ 函数 $y=\left(\dfrac{1}{2}\right)^{x}+\left(\dfrac{1}{3}\right)^{x}$ 在 $(－∞,1]$ 上为减函数，
   $∴$ 当 $x=1$ 时， $y=\left(\dfrac{1}{2}\right)^{x}+\left(\dfrac{1}{3}\right)^{x}$ 有最小值．
   $∴$ 只需 $m \leq \dfrac{5}{6}$ 即可．
    

【B组---提高题】

1. 如图所示，函数 $y=|2^x－2|$ 的图象是 (　　)
 A． $\qquad \qquad$ B． $\qquad \qquad$ C． $\qquad \qquad$ D．
 

2. 已知实数 $a,b$ 满足等式 $2^a=3^b$，下列五个关系式：①$0<b<a$；②$a<b<0；$③$0<a<b$；④$b<a<0$；⑤$a=b$．其中可能成立的关系式有 (　　)
 A．①②③ $\qquad \qquad$ B．①②⑤ $\qquad \qquad$ C．①③⑤ $\qquad \qquad$ D．③④⑤
 

3. 已知 $a=2^{\frac{4}{3}}, b=4^{\frac{2}{5}}, c=25^{\frac{1}{3}}$，则 (　　)
 A．$b<a<c$ $\qquad \qquad$ B．$a<b<c$ $\qquad \qquad$C．$b<c<a$ $\qquad \qquad$ D．$c<a<b$
 

4. 若方程 $\left(\dfrac{1}{4}\right)^{x}+\left(\dfrac{1}{2}\right)^{x}-1+a=0$ 有正数解，则实数 $a$ 的取值范围是 (　　)
  A．$(0,1)$ $\qquad \qquad$ B．$(-3,0)$ $\qquad \qquad$ C．$(-2,0)$ $\qquad \qquad$ D．$(-1,0)$
 

5. 设函数 $f(x)=|2^x-1|$，$c<b<a$，且 $f(c)>f(a)>f(b)$，则 $2^a+2^c$ 与 $2$ 的大小关系是 (　　)
 A．$2^a+2^c>2$ $\qquad \qquad$ B．$2^a+2^c≥2$$\qquad \qquad$ C．$2^a+2^c≤2$ $\qquad \qquad$ D．$2^a+2^c<2$
 

6. 已知不等式 $\dfrac{1}{2^{x^{2}+x}}>\left(\dfrac{1}{2}\right)^{2 x^{2}-m x+m+4}$ 对任意 $x∈R$ 恒成立，则实数 $m$ 的取值范围是 $\underline{\quad \quad}$．
 

7. 已知函数 $f(x)=\dfrac{1}{2^{x}+1}-\dfrac{1}{2}$．
(1) 求证：函数 $f(x)$ 是 $R$ 上的奇函数；
(2) 若对任意的 $t∈R$，不等式 $f(t^2-2t)+f(2t^2-k)<0$ 恒成立，求 $k$ 的取值范围．
 
 

参考答案

1. 答案 $B$
   解析 $\because y=\left|2^{x}-2\right|=\left\{\begin{array}{l} 2^{x}-2, x \geq 1 \\ 2-2^{x}, x<1 \end{array}\right.$，$∴x=1$ 时，$y=0$，$x≠1$ 时，$y>0$．故选 $B$．

2. 答案 $B$
   解析 令 $f(x)=2^x$ 和 $g(x)=3^x$，$2^a=3^b$ 即 $f(a)=g(b)$，如图所示
   由图象可知①②⑤正确，故选 $B$．
   

3. 答案 $A$
   解析 $\because a=2^{\frac{4}{3}}, \quad b=2^{\frac{4}{5}}, \dfrac{4}{3}>\dfrac{4}{5}$，$∴a>b$，
   又 $a=2^{\frac{4}{3}}=\sqrt[3]{16}, \quad c=\sqrt[3]{25}$，故 $a<c$，故 $c>a>b$，
   故选：$A$．

4. 答案 $B$
   解析 设 $t=\left(\dfrac{1}{2}\right)^{x}$ ，则有 $a=-\left[\left(\dfrac{1}{2}\right)^{2 x}+2\left(\dfrac{1}{2}\right)^{x}\right]=-t^{2}-2 t=-(t+1)^{2}+1$．
   原方程有正数解 $x>0$，则 $0<t=\left(\dfrac{1}{2}\right)^{x}<\left(\dfrac{1}{2}\right)^{0}=1$，
   即关于 $t$ 的方程 $t^2+2t+a=0$ 在 $(0,1)$ 上有实根．
   又因为 $a=-(t+1)^2+1$，
   所以当 $0<t<1$ 时有 $1<t+1<2$，
   即 $1<(t+1)^2<4$，
   即 $-4<-(t+1)^2<－1$，
   即 $-3<-(t+1)^2+1<0$，
   即得：$-3<a<0$，
   故选：$B$．

5. 答案 $D$
   解析 $f(x)=\left|2^{x}-1\right|=\left\{\begin{array}{l} 2^{x}-1, x \geq 0 \\ 1-2^{x}, x<0 \end{array}\right.$，
   作出 $f(x)=|2^x－1|$ 的图象如图所示，
   
   由图可知，要使 $c<b<a$ 且 $f(c)>f(a)>f(b)$ 成立，则有 $c<0$ 且 $a>0$，
   故必有 $2^c<1$ 且 $2^a>1$，
   又 $f(c)-f(a)>0$，即为 $1-2^c-(2^a-1)>0$，$∴2^a+2^c<2$．
   故选：$D$．

6. 答案 $(-3,5)$
   解析 不等式等价为 $\dfrac{1}{2^{x^{2}+x}}>\left(\dfrac{1}{2}\right)^{2 x^{2}-m x+m+4}$，
   即 $x^2+x<2x^2－mx+m+4$ 恒成立，$∴x^2-(m+1)x+m+4>0$ 恒成立，
   即 $△=(m+1)^2－4(m+4)<0$，即 $m^2-2m-15<0$，
   解得 $-3<m<5$，
   故答案为：$-3<m<5$．

7. 答案 (1) 奇函数 (2) $\left(-\infty,-\dfrac{1}{3}\right)$
   解析 (1)$f(x)$ 的定义域是 $R$， $f(-x)=\dfrac{1}{2^{-x}+1}-\dfrac{1}{2}=\dfrac{2^{x}}{1+2^{x}}-\dfrac{1}{2}$．
   $\therefore f(-x)+f(x)=\dfrac{2^{x}}{1+2^{x}}-\dfrac{1}{2}+\dfrac{1}{2^{x}+1}-\dfrac{1}{2}=\dfrac{2^{x}+1}{1+2^{x}}-1=0$．
   $∴f(-x)=-f(x)$．
   $∴f(x)$ 是 $R$ 上的奇函数．
   (2)$∵y=2^x$ 在 $R$ 上是增函数， $\therefore f(x)=\dfrac{1}{2^{x}+1}-\dfrac{1}{2}$ 在 $R$ 上是减函数．
   $∵f(t^2-2t)+f(2t^2-k)<0$，$∴f(t^2-2t)<-f(2t^2-k)=f(k-2t^2 )$．
   $∴t^2-2t>k-2t^2$，即 $k<3t^2-2t$．
   令 $g(t)=3 t^{2}-2 t=3\left(t-\dfrac{1}{3}\right)^{2}-\dfrac{1}{3}$，则 $g(t)$ 的最小值为 $-\dfrac{1}{3}$．
   $\therefore k<-\dfrac{1}{3}$．$∴k$ 的取值范围是 $\left(-\infty,-\dfrac{1}{3}\right)$．
    

【C组---拓展题】

1. 若 $2^{x}-5^{-x} \leq 2^{-y}-5^{y}$，则有 (　　)
 A．$x+y≥0$ $\qquad \qquad$ B．$x+y≤0$ $\qquad \qquad$ C．$x-y≤0$ $\qquad \qquad$ D．$x-y≥0$
 

2. 已知定义在 $(-1,1)$ 上的奇函数 $f(x)$．在 $x∈(-1,0)$ 时， $f(x)=2^{x}+2^{-x}$．
  (1) 试求 $f(x)$ 的表达式；
  (2) 若对于 $x∈(0,1)$ 上的每一个值，不等式 $t·2^x·f(x)<4^x-1$ 恒成立，求实数 $t$ 的取值范围．
 
 

参考答案

1. 答案 $B$
   解析 构造函数 $f(x)=2^{x}-5^{-x}$，易得函数 $f(x)$ 单调递增，
   由 $2^{x}-5^{-x} \leq 2^{-y}-5^{y}$，可得 $f(x)≤f(-y)$
   $∴x≤-y⇒x+y≤0$，
   故选：$B$．

2. 答案 (1) $f(x)=\left\{\begin{array}{cc} 2^{x}+2^{-x} & x \in(-1,0) \\ 0 & x=0 \\ -2^{x}-2^{-x} & x \in(0,1) \end{array}\right.$(2)$[0,+∞)$
   解析 (1)$∵f(x)$ 是定义在 $(-1,1)$ 上的奇函数，$∴f(0)=0$，
   设 $x∈(0,1)$，则 $-x∈(-1,0)$，
   则 $f(x)=-f(-x)=-\left(2^{x}+2^{-x}\right)$，
   故 $f(x)=\left\{\begin{array}{cc} 2^{x}+2^{-x} & x \in(-1,0) \\ 0 & x=0 \\ -2^{x}-2^{-x} & x \in(0,1) \end{array}\right.$
   (2) 由题意，$t·2^x·f(x)<4^x-1$ 可化为 $t \cdot 2^{x} \cdot\left(-2^{x}-2^{-x}\right)<4^{x}-1$
   化简可得 $t>\dfrac{-4^{x}+1}{4^{x}+1}$，
   (此处恒成立问题用到 “分离参数法” 转化为最值问题)
   令 $g(x)=\dfrac{-4^{x}+1}{4^{x}+1}=-1+\dfrac{2}{4^{x}+1}$， (分离常数法)
   易得 $g(x)$ 在 $(0,1)$ 上递减，
   $\therefore g(x)<g(0)=-1+\dfrac{2}{4^{0}+1}=0$，
   故 $t≥0$．($t$ 可取到 $0$).