3.2.2 函数的奇偶性
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
【基础过关系列】2022-2023学年高一数学上学期同步知识点剖析精品讲义(人教A版2019)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第一册同步巩固,难度2颗星!
基础知识
函数奇偶性的概念
(1) 一般地,设函数\(f(x)\)的定义域为\(I\),如果\(∀x∈I\),都有\(-x∈I\),且\(f(-x)=f(x)\),
那么函数\(f(x)\)就叫做偶函数.
(2) 一般地,设函数\(f(x)\)的定义域为\(I\),如果\(∀x∈I\),都有\(-x∈I\),且\(f(-x)=-f(x)\),
那么函数\(f(x)\)就叫做奇函数.
由奇偶函数的概念可知道其定义域I是关于原点对称的.
注 ① 从定义可知,若\(x\)是函数定义域中的一个数值,则\(-x\)也必然在该定义域中.故判断函数的奇偶性的前提是:定义域关于原点对称.如\(f(x)=x,x∈(-1,1]\)是非奇非偶函数.
② 函数按奇偶性可以分为四类:奇函数,偶函数,既是奇函数又是偶函数,既不是奇函数又不是偶函数.从定义可知,既是奇函数又是偶函数的函数只有一类,即\(f(x)=0\),\(x∈D\),\(D\)是关于原点对称的实数集.
性质
1 偶函数关于\(y\)轴对称;
2 奇函数关于原点对称;
3 若奇函数\(f(x)\)定义域内含有\(0\),则\(f(0)=0\);
证明 \(∵f(x)\)为奇函数,\(∴f(-x)=-f(x)\).
令\(x=0\),则\(f(-0)=-f(0)\),即\(f(0)=-f(0)\),\(∴f(0)=0\).
4 在公共定义域内,两个偶函数(或奇函数)的和(或差)仍是偶函数(或奇函数),两个偶函数(或奇函数)的积(或商)是偶函数,一个偶函数与一个奇函数的积(或商)是奇函数.
【例】设奇函数\(f(x)\)的定义域是\([-2,2]\)且图象的一部分如图所示,则不等式\(f(x)<0\)的解集是\(\underline{\quad \quad}\).

解析 由于\(f(x)\)是奇函数,所以\(f(x)\)的图象关于原点对称,补全其图象,如图所示.从图上可以看出\(f(x)<0\)的解集是\((-1,0)∪(1,2)\).

【练】如图,给出了偶函数\(y=f(x)\)的局部图象,试比较\(f(1)\)与\(f(3)\)的大小.

解析 \(∵\)函数\(f(x)\)是偶函数,\(∴\)其图象关于\(y\)轴对称,如图.

由图象可知\(f(1)<f(3)\).
判断函数奇偶性的方法
1 定义法
先判断定义域是否关于原点对称,再求\(f(-x)\), 看下与\(f(x)\)的关系:若\(f(-x)=f(x)\),则\(y=f(x)\)是偶函数;
若\(f(-x)=-f(x)\),则\(y=f(x)\)是奇函数.
2 数形结合
若函数关于原点对称,则函数是奇函数;若函数关于\(y\)轴对称,则函数是偶函数.
3 取特殊值排除法(选择题)
比如:若根据函数得到\(f(1)≠f(-1)\),则排除\(f(x)\)是偶函数.
4 性质法
偶函数的和、差、积、商(分母不为\(0\))仍为偶函数;奇函数的和、差 (分母不为\(0\))仍为奇函数;
奇(偶)数个奇函数的积为奇(偶)函数;两个奇函数的商(分母不为0)为偶函数;
一个奇函数与偶函数的积为奇函数.
对于复合函数\(F(x)=f(g(x))\)的奇偶性如下图
| \(g(x)\) | \(f(x)\) | \(F(x)\) |
|---|---|---|
| 偶函数 | 偶函数 | 偶函数 |
| 奇函数 | 奇函数 | 奇函数 |
| 偶函数 | 奇函数 | 偶函数 |
| 奇函数 | 偶函数 | 偶函数 |
基本方法
【题型1】判断函数的奇偶性
【典题1】 判断下列函数的奇偶性
(1) \(f(x)=\dfrac{2 x^{2}+2 x}{x+1}\); \(\qquad\) (2) \(f(x)=\sqrt{x^{2}-1}+\sqrt{1-x^{2}}\);\(\qquad\) (3) \(f(x)=x^3-2x\);\(\qquad\)
(4) \(f(x)=\dfrac{|x|}{x^{2}+1}\); \(\qquad\) (5)\(f(x)=|x^2+x|\).
解析 (1)函数的定义域为\((-∞,-1)∪(-1,+∞)\)不关于原点对称,
故函数\(f(x)\)既不是奇函数,又不是偶函数.
(2) \(∵\)函数的定义域为\(\{-1,1\}\)且\(f(x)=0\),\(f(-1)=0\),\(f(1)=0\),
\(∴f(-1)=f(1)\)且\(f(-1)=-f(1)\).
\(∴\)函数 \(f(x)=\sqrt{x^{2}-1}+\sqrt{1-x^{2}}\)既是奇函数,又是偶函数.
(3)函数的定义域为\(R\),
\(∵f(-x)=(-x)^3-2(-x)=-(x^3-2x)=-f(x)\),
\(∴\)函数\(f(x)=x^3-2x\)是奇函数.
(4)函数的定义域为\(R\).
方法1 \(\because f(-x)=\dfrac{|-x|}{(-x)^{2}+1}=\dfrac{|x|}{x^{2}+1}=f(x)\),\(∴\)函数 \(f(x)=\dfrac{|x|}{x^{2}+1}\)是偶函数.
方法2 \(∵y=|x|\)和\(y=x^2+1\)是偶函数,\(∴\)函数 \(f(x)=\dfrac{|x|}{x^{2}+1}\)是偶函数.
(5) 方法1 \(f(1)=2\),\(f(-1)=0\),则\(f(1)≠f(-1)\),即\(f(x)\)不是偶函数;
\(f(1)+f(-1)≠0\),即\(f(x)\)不是奇函数;
故\(f(x)\)既不是奇函数,又不是偶函数.
方法2 画出函数图象如下图,
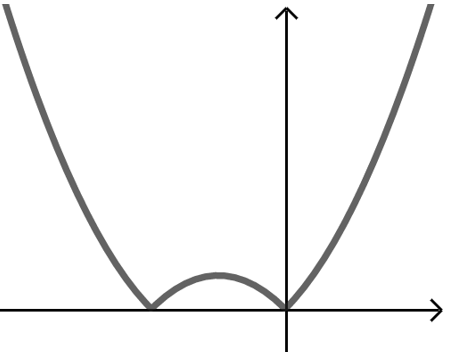
函数图象即不关于\(y\)轴对称,也不关于原点对称,
故\(f(x)\)既不是奇函数,又不是偶函数.
点拨
判断函数的奇偶性的方法有
① 定义法
先判断定义域是否关于原点对称,再求\(f(-x)\) , 看下与\(f(x)\)的关系:
若\(f(-x)=f(x)\),则\(y=f(x)\)是偶函数;若\(f(-x)=-f(x)\),则\(y=f(x)\)是奇函数.
② 数形结合
若函数关于原点对称,则函数是奇函数;若函数关于\(y\)轴对称,则函数是偶函数.
③ 取特殊值排除法(选择题)
④ 性质法
偶函数的和、差、积、商(分母不为\(0\))仍为偶函数;奇函数的和、差 (分母不为\(0\))仍为奇函数;
奇(偶)数个奇函数的积为奇(偶)函数;两个奇函数的商(分母不为0)为偶函数;
一个奇函数与偶函数的积为奇函数.
巩固练习
1.函数\(y=x^3-x\)的奇偶性为 ( )
A.奇函数 \(\qquad \qquad\) B.偶函数 \(\qquad \qquad\) C.既是奇函数又是偶函数 \(\qquad \qquad\) D.非奇非偶函数
2.设\(f(x)\)是定义在\(R\)上的一个函数,则函数\(F(x)=f(x)-f(-x)\)在\(R\)上一定是( )
A.奇函数 \(\qquad \qquad\) B.偶函数 \(\qquad \qquad\) C.既是奇函数又是偶函数 \(\qquad \qquad\) D.非奇非偶函数
3.如果定义在区间\([3-a,5]\)上的函数\(f(x)\)为奇函数,那么\(a=\)\(\underline{\quad \quad}\) .
4.判断函数 \(f(x)=\left\{\begin{array}{l}
\dfrac{1}{2} x^{2}+1,(x>0) \\
-\dfrac{1}{2} x^{2}-1,(x<0)
\end{array}\right.\)的奇偶性.
参考答案
- 答案 \(A\)
解析 \(f(-x)=-x^3+x=-f(x)\),\(f(x)\)是奇函数. - 答案 \(A\)
解析 \(F(-x)=f(-x)-f(x)=-F(x)\),\(F(x)\)是奇函数. - 答案 \(\dfrac{1}{2}\)
解析 \(∵f(x)\)是\([3-a,5]\)上的奇函数,\(∴\)区间\([3-a,5]\)关于原点对称,
\(∴3-a=-5\),\(a=8\). - 答案 奇函数
解析 解法一:函数的定义域为\((-∞,0)∪(0,+∞)\),
当\(x>0\)时,\(-x<0\), \(f(-x)=-\dfrac{1}{2}(-x)^{2}-1=-\left(\dfrac{1}{2} x^{2}+1\right)=-f(x)\).
当\(x<0\)时,\(-x>0\),
\(f(-x)=\dfrac{1}{2}(-x)^{2}+1=\dfrac{1}{2} x^{2}+1=-\left(-\dfrac{1}{2} x^{2}-1\right)=-f(x)\).
综上所述,在\((-∞,0)∪(0,+∞)\)上总有\(f(-x)=-f(x)\).
因此函数\(f(x)\)是奇函数.
解法二:作出函数的图象,如图所示.

函数\(f(x)\)的图象关于原点对称,所以\(f(x)\)是奇函数.
【题型2】函数奇偶性的运用
【典题1】 若函数 \(f(x)=\dfrac{2^{x}-a}{2^{x}+1}\)的图象关于\(y\)轴对称,则常数\(a=\) ( )
A.\(-1\) \(\qquad \qquad\) B.\(1\) \(\qquad \qquad\) C.\(1\)或\(-1\) \(\qquad \qquad\) D.不存在
解析 可知函数\(f(x)\)为偶函数,则\(f(-x)=f(x)\),
令\(x=1\)得,\(f(-1)=f(1)\),即 \(\dfrac{2^{-1}-a}{2^{-1}+1}=\dfrac{2-a}{2+1}\),解得\(a=-1\),
将\(a=-1\)代入解析式验证,符合题意.故选:\(A\).
点拨 函数\(f(x)\)为偶函数,则\(f(-x)=f(x)\)是对于定义域内任意\(x\)均成立的,故本题令\(x=1\)求得\(a\),但最后需要检验.解答题这样求解不够严谨.
【典题2】 已知函数\(f(x)\)是定义域为\(R\)的奇函数,当\(x≥0\)时,\(f(x)=2^x+2x-a\),则\(f(-1)=\) \(\underline{\quad \quad}\).
解析 根据题意,函数\(f(x)\)是定义域为\(R\)的奇函数,则\(f(0)=0\),
则有\(f(0)=2^0-a=1-a=0\),解可得\(a=1\),
则\(f(1)=2+2-a=4-1=3\),
又由\(f(x)\)为奇函数,则\(f(-1)=-f(1)=-3\).
点拨 若奇函数\(f(x)\)的定义域内能取到\(0\),则\(f(0)=0\).
【典题3】 已知函数\(f(x)\)是定义在\(R\)上的偶函数,当\(x (-∞,0)\)时,\(f(x)=x-x^4\),则当 \(x∈(-∞,0)\)时,\(f(x)=\) \(\underline{\quad \quad}\).
解析 设\(x>0\),则\(-x<0\),则 \(f(-x)=-x-(-x)^{4}=-x-x^{4}\).
又\(∵y=f(x)\)是偶函数,
\(∴f(x)=f(-x)\),\(x>0\),
从而在区间\((0,+∞)\)上的函数表达式为\(f(x)=-x-x^4\).
巩固练习
1.设函数\(f(x)\)是定义在\(R\)上的奇函数,且\(f(-1)=1\),则\(f(1)+f(0)=\)( )
A.\(1\) \(\qquad \qquad\) B.\(0\)\(\qquad \qquad\) C.\(-1\) \(\qquad \qquad\) D.\(-2\)
2.已知函数\(f(x)\)是奇函数,当\(x<0\)时,\(f(x)=-2x^2+x\),则\(f(2)=\)( )
A.\(-6\) \(\qquad \qquad\) B.\(6\) \(\qquad \qquad\) C.\(-10\) \(\qquad \qquad\) D.\(10\)
3.若函数 \(f(x)=\dfrac{(2 x+1)(x-a)}{x}(a \in R)\)为奇函数,则实数\(a=\)( )
A. \(\dfrac{1}{2}\) \(\qquad \qquad\) B.\(0\) \(\qquad \qquad\) C.\(-1\) \(\qquad \qquad\) D.\(1\)
4.已知函数 \(f(x)=a x+\dfrac{x}{4^{x}+1}\)是偶函数,则常数\(a\)的值为\(\underline{\quad \quad}\).
5.已知\(f(x)\)为定义在\(R\)上的奇函数,当\(x≥0\)时,\(f(x)=2^x+m\),则\(f(-2)=\) \(\underline{\quad \quad}\).
参考答案
- 答案 \(C\)
解析 根据题意,函数\(f(x)\)是定义在\(R\)上的奇函数,则\(f(0)=0\),
若\(f(-1)=1\),则\(f(1)=-f(-1)=-1\),
则\(f(1)+f(0)=-1\);故选\(C\). - 答案 \(D\)
解析 \(∵f(x)\)是奇函数,当\(x<0\)时,\(f(x)=-2x^2+x\),
\(∴f(-2)=-8-2=-10\),即\(-f(2)=-10\),则\(f(2)=10\),故选:\(D\). - 答案 \(A\)
解析 根据题意,函数 \(f(x)=\dfrac{(2 x+1)(x-a)}{x}(a \in R)\)为奇函数,
则\(f(-x)=-f(x)\),即 \(\dfrac{(2 x+1)(x-a)}{x}=\dfrac{(-2 x+1)(-x-a)}{-x}\),
变形可得\((2a-1)x=0\),则有 \(a=\dfrac{1}{2}\);故选\(A\). - 答案 \(-\dfrac{1}{2}\)
解析 易知函数定义域为\(R\)
\(∵\)函数 \(f(x)=a x+\dfrac{x}{4^{x}+1}\)是偶函数
\(∴f(-x)=f(x)\)对定义域内每一个\(x\)都成立
\(\therefore-a x+\dfrac{-x}{4^{-x}+1}=a x+\dfrac{x}{4^{x}+1}\),
\(\therefore-2 a x=\dfrac{x}{4^{x}+1}+\dfrac{x}{4^{-x}+1}=\dfrac{x}{4^{x}+1}+\dfrac{x \times 4^{x}}{4^{-x}\left(4^{x}+1\right)}\)\(=\dfrac{x}{4^{x}+1}+\dfrac{x \times 4^{x}}{1+4^{x}}=x\),
\(∴(1+2a)x=0\)对定义域内每一个x都成立
\(∴1+2a=0\),即 \(a=-\dfrac{1}{2}\). - 答案 \(-3\)
解析 根据题意,\(f(x)\)为定义在\(R\)上的奇函数,则\(f(0)=2^0+m=0\),
解可得:\(m=-1\),
即当\(x≥0\)时,\(f(x)=2^x-1\),则有\(f(2)=2^2-1=3\),
又由\(f(x)\)为奇函数,则\(f(-2)=-f(2)=-3\).
【题型3】函数的奇偶性与单调性的综合
【典题1】 若函数\(f(x)\)是定义在\([-6,6]\)上的偶函数,且在\([-6,0]\)上单调递减,则( )
A.\(f(3)+f(4)>0\) \(\qquad \qquad \qquad\) B.\(f(-3)-f(-2)<0\) \(\qquad \qquad\)
C.\(f(-2)+f(-5)<5\) \(\qquad \qquad\) D.\(f(4)-f(-1)>0\)
解析 \(f(x)\)是定义在\([-6,6]\)上的偶函数,且在\([-6,0]\)上单调递减,
可得\(f(x)\)在\([0,6]\)上单调递增,
依题意有\(-4<-1⇒f(-4)>f(-1)⇒f(4)-f(-1)>0\).
点拨 涉及到函数奇偶性和单调性,可借助函数的图象去理解消化.
【典题2】函数 \(f(x)=\dfrac{a x+b}{1+x^{2}}\)是定义在区间\((-1,1)\)上的奇函数,且 \(f\left(\dfrac{1}{2}\right)=\dfrac{2}{5}\).
(1)确定函数\(f(x)\)的解析式;
(2)用定义证明:\(f(x)\)在区间\((-1,1)\)上是增函数;
(3)解不等式:\(f(t-1)+f(t)<0\).
解析 (1)由题意知 \(\left\{\begin{array}{l}
f(0)=0 \\
f\left(\dfrac{1}{2}\right)=\dfrac{2}{5}
\end{array}\right.\),即 \(\left\{\begin{array}{l}
\dfrac{b}{1+0^{2}}=0 \\
\dfrac{\dfrac{a}{2}+b}{1+\dfrac{1}{4}}=\dfrac{2}{5}
\end{array}\right.\),解得 \(\left\{\begin{array}{l}
a=1 \\
b=0
\end{array}\right.\),
故 \(f(x)=\dfrac{x}{1+x^{2}}\).
(2)任取\(-1<x_1<x_2<1\),则\(x_2-x_1>0\),(定义法证明)
\(f\left(x_{2}\right)-f\left(x_{1}\right)=\dfrac{x_{2}}{1+x_{2}^{2}}-\dfrac{x_{1}}{1+x_{1}^{2}}=\dfrac{\left(x_{2}-x_{1}\right)\left(1-x_{1} x_{2}\right)}{\left(1+x_{1}^{2}\right)\left(1+x_{2}^{2}\right)}\).
\(∵-1<x_1<x_2<1\),
\(∴-1<x_1 x_2<1,1-x_1 x_2>0\).
于是\(f(x_2 )-f(x_1 )>0\),
\(∴f(x)\)为区间\((-1,1)\)上的增函数.
(3)\(f(t-1)<-f(t)=f(-t)\),
\(∵f(x)\)在区间\((-1,1)\)上是增函数,
\(∴-1<t-1<-t<1\),解得 \(0<t<\dfrac{1}{2}\).
点拨 求解类似\(f(x)<f(a)\)关于\(x\)的不等式,可利用函数的单调性去掉\(f\)求解,若强行代入解析式就比较暴力了.
巩固练习
1.奇函数\(f(x)\)在区间\([3,7]\)上是增函数,在区间\([3,6]\)上的最大值为\(8\),最小值为\(-1\),则\(2f(-6)+f(-3)\)的值为\(\underline{\quad \quad}\) .
2.设偶函数\(f(x)\)的定义域为\(R\),当 \(x∈[0,+∞)\)时,\(f(x)\)是增函数,则\(f(-2),f(π),f(-3)\)由大到小的关系是\(\underline{\quad \quad}\).
3.已知偶函数\(f(x)\)在\([0,+∞)\)上为增函数,且\(f(x-1)>f(3-2x)\),则实数\(x\)的取值范围是\(\underline{\quad \quad}\) .
4.已知偶函数\(f(x)\)在区间\([0,+∞)\)单调增加,则满足 \(f(2 x-1)<f\left(\dfrac{1}{3}\right)\)的\(x\)取值范围是\(\underline{\quad \quad}\) .
参考答案
- 答案 \(-15\)
解析 \(f(x)\)在\([3,6]\)上为增函数, \(f(x)_{\max }=f(6)=8\), \(f(x)_{\min }=f(3)=-1\).
\(∴2f(-6)+f(-3)=-2f(6)-f(3)=-2×8+1=-15\). - 答案 \(f(π)>f(-3)>f(-2)\)
解析 利用函数\(f(x)\)为\(R\)上的偶函数,将\(f(-2),f(-3)\)转化到区间\([0,+∞)\)上,
利用\(f(x)\)在此区间上是增函数比较大小.因为\(f(x)\)为\(R\)上的偶函数,
所以\(f(-2)=f(2),f(-3)=f(3)\).
又因为当\(x∈[0,+∞)\)时,\(f(x)\)是增函数,且\(π>3>2\),
所以\(f(π)>f(3)>f(2)\),故\(f(π)>f(-3)>f(-2)\). - 答案 \(\left(\dfrac{4}{3}, 2\right)\)
解析 \(∵\)偶函数\(f(x)\)在\([0,+∞)\)上为增函数;
\(∴\)由\(f(x-1)>f(3-2x)\)得,\(f(|x-1|)>f(|3-2x|)\);
\(∴|x-1|>|3-2x|\);
\(∴(x-1)^2>(3-2x)^2\);整理得\(3x^2-10x+8<0\);解得 \(\dfrac{4}{3}<x<2\);
\(∴\)实数\(x\)的取值范围是 \(\left(\dfrac{4}{3}, 2\right)\). - 答案 \(\left(\dfrac{1}{3}, \dfrac{2}{3}\right)\)
解析 由于\(f(x)\)是偶函数,故\(f(x)=f(|x|)\)
\(∴\)得 \(f(|2 x-1|)<f\left(\dfrac{1}{3}\right)\),
再根据\(f(x)\)的单调性得 \(|2 x-1|<\dfrac{1}{3}\),解得 \(\dfrac{1}{3}<x<\dfrac{2}{3}\).
分层练习
【A组---基础题】
1.已知\(f(x)=ax^2+bx\)是定义在\([a-1,2a]\)上的偶函数,那么\(a+b\)的值是( )
A. \(-\dfrac{1}{3}\) \(\qquad \qquad\) B. \(\dfrac{1}{3}\) \(\qquad \qquad\) C.\(-\dfrac{1}{2}\) \(\qquad \qquad\) D. \(\dfrac{1}{2}\)
2.下列说法正确的是( )
A.若一个函数的定义域关于坐标原点对称,则这个函数为奇函数
B.若一个函数为偶函数,则它的定义域关于坐标原点对称
C.若一个函数的定义域关于坐标原点对称,则这个函数为偶函数
D.若函数\(f(x)\)的定义域为\(R\),且\(f(0)=0\),则\(f(x)\)是奇函数
3.函数\(f(x)=|x|+1\)是( )
A.奇函数 \(\qquad \qquad\) B.偶函数 \(\qquad \qquad\) C.既是奇函数又是偶函数 \(\qquad \qquad\) D.非奇非偶函数
4.函数 \(f(x)=\dfrac{\sqrt{3-x^{2}}}{x}\)的图象关于( )
A.原点对称 \(\qquad \qquad\) B.轴对称 \(\qquad \qquad\) C.\(y\)轴对称 \(\qquad \qquad\) D.直线\(y=x\)对称
5.已知函数 \(f(x)=x^5-ax^3+bx+2\),\(f(-5)=17\),则\(f(5)\)的值是( )
A.\(19\) \(\qquad \qquad\) B.\(13\) \(\qquad \qquad\) C.\(-19\) \(\qquad \qquad\) D.\(-13\)
6.设\(f(x)\)是奇函数,且当\(x∈(0,+∞)\)时,\(f(x)=x(1+x)\),则当\(x∈(-∞,0)\)时,\(f(x)\)等于( )
A.\(x(1+x)\) \(\qquad \qquad\) B.\(-x(1+x)\) \(\qquad \qquad\) C.\(x(1-x)\) \(\qquad \qquad\) D.\(-x(1-x)\)
7.如果奇函数\(f(x)\)在区间\([1,5]\)上是减函数,且最小值为\(6\),那么\(f(x)\)在区间\([-5,-1]\)上是( )
A.减函数且最大值为\(-6\) \(\qquad \qquad\) B.增函数且最大值为\(6\)
C.减函数且最小值为\(-6\) \(\qquad \qquad\) D.增函数且最小值为\(6\)
8.若偶函数\(f(x)\)在\((-∞,-1]\)上是减函数,则 ( )
A. \(f\left(-\dfrac{3}{2}\right)<f(-1)<f(2)\) \(\qquad \qquad\) B. \(f(-1)<f\left(-\dfrac{3}{2}\right)<f(2)\)
C. \(f(2)<f(-1)<f\left(-\dfrac{3}{2}\right)\) \(\qquad \qquad\) D.\(f(2)<f\left(-\dfrac{3}{2}\right)<f(-1)\)
9.若函数\(f(x)=ax^2+bx+3a+b\)是偶函数,且定义域为\([a-1,2a]\),则\(a=\)\(\underline{\quad \quad}\) , \(b=\) \(\underline{\quad \quad}\).
10.已知函数 \(f(x)=\left\{\begin{array}{l}
-x^{2}+2 x, x>0 \\
0, x=0 \\
x^{2}+m x, x<0
\end{array}\right.\)是奇函数,则\(m=\) \(\underline{\quad \quad}\).
11.已知函数 \(f(x)=\dfrac{a x+b}{1+x^{2}}\)是定义域为\((-1,1)\)上的奇函数,且\(a>0\).
(1)用定义证明:函数\(f(x)\)在\((-1,1)\)上是增函数;
(2)若实数\(t\)满足\(f(2t-1)+f(t-1)<0\),求实数\(t\)的范围.
参考答案
-
答案 \(B\)
解析 依题意得:\(f(-x)=f(x)\),\(∴b=0\),
又\(a-1=-2a\), \(\therefore a=\dfrac{1}{3}\), \(\therefore a+b=\dfrac{1}{3}\).故选:\(B\). -
答案 \(B\)
解析 奇偶函数的定义域一定关于原点对称,但定义域关于原点对称的函数不一定具有奇偶性,如\(y=x+1\).由此可判断\(A、C\)项错误,\(B\)项正确.奇函数若在原点处有定义,则\(f(0)=0\),反之不一定成立,如\(y=x^2\),因此\(D\)项错误.故选\(B\). -
答案 \(B\)
-
答案 \(A\)
解析 根据题意, \(f(x)=\dfrac{\sqrt{3-x^{2}}}{x}\),有 \(f(-x)=-\dfrac{\sqrt{3-x^{2}}}{x}\),
则有\(f(-x)=-f(x)\),其图象关于原点对称,故选:\(A\). -
答案 \(D\)
解析 \(\because g(x)=x^{5}-a x^{3}+b x\)是奇函数 \(∴g(-x)=-g(x)\)
\(∵f(-5)=17=g(-5)+2\) \(∴g(5)=-15\)
\(∴f(5)=g(5)+2=-15+2=-13\),故选:\(D\). -
答案 \(C\)
解析 当\(x>0\)时,\(-x<0\),代入函数在\((-∞,0)\)上的解析式,即得\(f(-x)=-x(1-x)\),
\(∵f(x)\)是奇函数,\(∴f(x)=-f(-x)=x(1-x)\),
故选:\(C\). -
答案 \(A\)
解析 当\(-5≤x≤-1\)时\(1≤-x≤5\),
\(∴f(-x)≥6\),即\(-f(x)≥6\).从而\(f(x)≤-6\),
又奇函数在原点两侧的对称区间上单调性相同,
故\(f(x)\)在\([-5,-1]\)是减函数.
故选:\(A\). -
答案 \(B\)
解析 根据题意,\(f(x)\)为偶函数,则\(f(2)=f(-2)\),
又由函数\(f(x)\)在\((-∞,-1]\)上是减函数,
则 \(f(-1)<f\left(-\dfrac{3}{2}\right)<f(-2)\),即 \(f(-1)<f\left(-\dfrac{3}{2}\right)<f(2)\),故选:\(B\). -
答案 \(\dfrac{1}{3}, 0\)
解析 \(∵\)偶函数的定义域关于原点对称,\(∴a-1=-2a\),解得 \(a=\dfrac{1}{3}\).
\(∴f(x)=\frac{1}{3}x^2+bx+b+1\)为二次函数.
\(∵\)函数\(f(x)\)为偶函数,对称轴 \(x=-\dfrac{b}{2 \times \dfrac{1}{3}}=0\),即\(b=0\). -
答案 \(2\)
解析 \(∵\)当\(x<0\)时,\(-x>0\), \(f(-x)=-(-x)^2+2(-x)=-x^2-2x\),
又\(f(x)\)为奇函数,\(∴f(-x)=-f(x)=-x^2-2x\).
\(∴f(x)=x^2+2x=x^2+mx\).\(∴m=2\). -
答案 (1)略 (2) \(\left(0, \dfrac{2}{3}\right)\)
解析 (1)\(∵\)函数 \(f(x)=\dfrac{a x+b}{1+x^{2}}\)是定义域为\((-1,1)\)上的奇函数,
\(\therefore f(0)=\dfrac{b}{1}=0\),\(∴b=0\),
\(\therefore f(x)=\dfrac{a x}{1+x^{2}}\)
任取\(x_1,x_2∈(-1,1)\),且\(x_1<x_2\),
\(\therefore f\left(x_{1}\right)-f\left(x_{2}\right)=\dfrac{a x_{1}}{1+x_{1}^{2}}-\dfrac{a x_{2}}{1+x_{2}^{2}}=\dfrac{a\left(x_{1}+x_{1} x_{2}^{2}-x_{2}-x_{2} x_{1}^{2}\right)}{\left(1+x_{1}^{2}\right)\left(1+x_{2}^{2}\right)}\)\(=\dfrac{a\left(x_{1}-x_{2}\right)\left(1-x_{1} x_{2}\right)}{\left(1+x_{1}^{2}\right)\left(1+x_{2}^{2}\right)}\),
\(∵a>0\),\(-1<x_1<x_2<1\),
\(∴x_1-x_2<0\),\(1-x_1 x_2>0\), \(1+x_1^2>0\),\(1+x_2^2>0\)
\(∴\)函数\(f(x)\)在\((-1,1)\)上是增函数.
(2)\(∵f(2t-1)+f(t-1)<0\),\(∴f(2t-1)<-f(t-1)\),
\(∵\)函数 \(f(x)=\dfrac{a x+b}{1+x^{2}}\)是定义域为\((-1,1)\)上的奇函数,且\(a>0\).
\(∴f(2t-1)<f(1-t)\),
\(∵\)函数\(f(x)\)在\((-1,1)\)上是增函数,
\(\therefore\left\{\begin{array}{l} 2 t-1<1-t \\ -1<2 t-1<1 \\ -1<1-t<1 \end{array}\right.\),解得 \(0<t<\dfrac{2}{3}\).
故实数\(t\)的范围是 \(\left(0, \dfrac{2}{3}\right)\).
【B组---提高题】
1.设\(f(x)\)是\(R\)上的任意函数,则下列叙述正确的是( )
A.\(f(x)f(-x)\)是奇函数 \(\qquad \qquad \qquad\) B.\(f(x)|f(-x)|\)是奇函数
C.\(f(x)-f(-x)\)是偶函数 \(\qquad \qquad\) D.\(f(x)+f(-x)\)是偶函数
2.若函数\(f (x) (x∈R)\)是奇函数,则 ( )
A.函数\(f(x^2 )\)是奇函数 \(\qquad \qquad\) B.函数\([f(x)]^2\)是奇函数
C.函数\(f(x)⋅x^2\)是奇函数 \(\qquad \qquad\)D.函数\(f(x)+x^2\)是奇函数
3.已知奇函数\(y=f(x)\)在\((-∞,0)\)为减函数,且\(f(2)=0\),则不等式\((x-1)f(x-1)>0\)的解集为( )
A.\(\{x|-3<x<-1\}\) \(\qquad \qquad \qquad\) B .\(\{x|-3<x<1\)或\(x>2\}\)
C.\(\{x|-3<x<0\)或\(x>3\}\) \(\qquad \qquad\) D.\(\{x|-1<x<1\)或\(1<x<3\}\)
4.已知\(f(x)\)是定义在\(R\)上的奇函数,当\(x>0\)时,\(f(x)\)为增函数,且\(f(3)=0\),那么不等式\(xf(x)<0\)的解集是( )
A.\((-3,-1)∪(1,3)\) \(\qquad \qquad\) B.\((-3,0)∪(3,+∞)\)
C.\((-3,0)∪(0,3)\) \(\qquad \qquad\) D.\((-∞,-3)∪(0,3)\)
5.若函数 \(f(x)=(1-x^2)(x^2+ax-5)\)的图象关于直线\(x=0\)对称,则\(f(x)\)的最大值是( )
A.\(-4\) \(\qquad \qquad\) B.\(4\)\(\qquad \qquad\) C.\(4\)或\(-4\) \(\qquad \qquad\) D.不存在
6.函数 \(f(x)=\dfrac{\sqrt{4-x^{2}}}{|x+3|-3}\)的图象关于\(\underline{\quad \quad}\)对称.
7.已知函数\(f(x)\)为偶函数,当\(x∈[-1,1]\)时, \(f(x)=\sqrt{1-x^{2}}\),且\(f(x+1)\)为奇函数,则 \(f\left(\dfrac{21}{2}\right)=\) \(\underline{\quad \quad}\).
8.已知函数\(f(x)=x^3+2x\),则不等式\(f(2x)+f(x-1)>0\)的解集为\(\underline{\quad \quad}\).
9.已知\(f(x)\),\(g(x)\)分别是\(R\)上的奇函数和偶函数,且\(f(x)+g(x)=3x^2-x+1\),试求\(f(x)\)和\(g(x)\)的表达式.
10.已知定义在\(R\)奇函数 \(f(x)=\dfrac{2^{x}-a}{2^{x}+b}\).
(1)求\(a,b\)的值; (2)判断并证明\(f(x)\)在\(R\)上的单调性; (3)求该函数的值域.
参考答案
-
答案 \(D\)
解析 选\(D\).设\(F(x)=f(x)f(-x)\),则\(F(-x)=F(x)\)为偶函数.
设\(G(x)=f(x)|f(-x)|\), 则\(G(-x)=f(-x)|f(x)|\).
\(∴G(x)\)与\(G(-x)\)关系不定.
设\(M(x)=f(x)-f(-x)\),\(∴M(-x)=f(-x)-f(x)=-M(x)\)为奇函数.
设\(N(x)=f(x)+f(-x)\),则\(N(-x)=f(-x)+f(x)\).
\(N(x)\)为偶函数. -
答案 \(C\)
-
答案 \(D\)
解析 由题意画出\(f(x)\)的草图如下,

因为\((x-1)f(x-1)>0\),所以\((x-1)\)与\(f(x-1)\)同号,
由图象可得\(-2<x-1<0\)或\(0<x-1<2\),
解得\(-1<x<1\)或\(1<x<3\),
故选:\(D\). -
答案 \(C\)
解析 \(∵f(x)\)为奇函数,且在\((0,+∞)\)上是增函数,\(f(3)=0\),
\(∴f(3)=-f(-3)=0\),在\((-∞,0)\)内是增函数
\(∴x f(x)<0\)则 \(\left\{\begin{array} { l } { x > 0 } \\ { f ( x ) < 0 = f ( 3 ) } \end{array} \text { 或 } \left\{\begin{array}{l} x<0 \\ f(x)>0=f(-3) \end{array}\right.\right.\)
根据在\((-∞,0)\)和\((0,+∞)\)内是都是增函数,解得\(x∈(-3,0)∪(0,3)\)
故选:\(C\). -
答案 \(B\)
解析 由函数\(f(x)=(1-x^2 )(x^2+ax-5)\)的图象关于直线\(x=0\)对称,知\(f(x)\)是偶函数,
\(∴f(-x)=f(x)\),即 \((1-x^2 )(x^2-ax-5)=(1-x^2 )(x^2+ax-5)\),
整理得\(2ax(x^2-1)=0\)总成立,得\(a=0\),
\(∴f(x)=(1-x^2 )(x^2-5)\),
令 \(x^2=t(t≥0)\),则 \(y=(1-t)(t-5)=-t^2+6t-5=-(t-3)^2+4\),
\(∴\)当\(t=3\)时,\(y\)有最大值\(4\),即\(f(x)\)的最大值是\(4\).
故选:\(B\). -
答案 原点
解析 要使函数有意义,则 \(\left\{\begin{array}{c} 4-x^{2} \geq 0 \\ |x+3|-3 \neq 0 \end{array}\right.\),即\((x-2)(x+2)<0\),
解得\(-2<x<0\)或\(0<x<2\),则定义域关于原点对称.
此时\(|x+3|=x+3\),则函数 \(f(x)=\dfrac{\sqrt{4-x^{2}}}{|x+3|-3}=\dfrac{\sqrt{4-x^{2}}}{x+3-3}=\dfrac{\sqrt{4-x^{2}}}{x}\),
\(\because f(-x)=-\dfrac{\sqrt{4-x^{2}}}{x}=-f(x)\),
\(∴\)函数\(f(x)\)是奇函数,图象关于原点对称. -
答案 \(-\dfrac{\sqrt{3}}{2}\)
解析 \(∵\)函数\(f(x)\)为偶函数,\(∴f(-x)=f(x)\).
又\(f(x+1)\)为奇函数,图象关于点\((0,0\))对称,
∴函数\(f(x)\)的图象关于点\((-1,0)\)对称,
\(∴f(x-2)=-f(-x)\),\(∴f(x-2)=-f(x)\),\(∴f(x-4)=f(x)\)
\(∴\)函数\(f(x)\)的周期\(4\),
\(\therefore f\left(\dfrac{21}{2}\right)=f\left(12-\dfrac{3}{2}\right)=f\left(-\dfrac{3}{2}\right)=-f\left(\dfrac{3}{2}-2\right)\)\(=-f\left(-\dfrac{1}{2}\right)=-\sqrt{1-\left(-\dfrac{1}{2}\right)^{2}}=-\dfrac{\sqrt{3}}{2}\). -
答案 \(\left(\dfrac{1}{3},+\infty\right)\)
解析 函数\(f(x)\)为奇函数,且函数\(f(x)\)为增函数,
则不等式\(f(2x)+f(x-1)>0\)等价为\(f(2x)>-f(x-1)=f(1-x)\),
则\(2x>1-x\),得\(3x>1\),得 \(x>\dfrac{1}{3}\),
即不等式的解集为 \(\left(\dfrac{1}{3},+\infty\right)\). -
答案 \(f(x)=-x,g(x)=3x^2+1\)
解析 以\(-x\)代替条件等式中的\(x\),则有\(f(-x)+g(-x)=3x^2+x+1\),
又\(f(x)\),\(g(x)\)分别是\(R\)上的奇函数和偶函数,
故\(-f(x)+g(x)=3x^2+x+1\).
又\(f(x)+g(x)=3x^2-x+1\),
联立可得\(f(x)=-x,g(x)=3x^2+1\). -
答案 (1) \(\left\{\begin{array}{l} a=1 \\ b=1 \end{array}\right.\) (2)\(f(x)\)在\(R\)上是增函数 (3) \((-1,1)\)
解析 (1)因为\(f(x)\)是\(R\)上的奇函数,所以 \(\left\{\begin{array}{l} f(0)=0 \\ f(-1)=-f(1) \end{array}\right.\),
即 \(\left\{\begin{array}{l} \dfrac{1-a}{1+b}=0 \\ \dfrac{1}{\dfrac{2}{2}-a}=-\dfrac{2-a}{\dfrac{1}{2}+b} \end{array}\right.\),解得 \(\left\{\begin{array}{l} a=1 \\ b=1 \end{array}\right.\);
(2)由(1)知 \(f(x)=\dfrac{2^{x}-1}{2^{x}+1}\),设\(x_1,x_2∈R\),且\(x_1<x_2\),
则 \(f\left(x_{1}\right)-f\left(x_{2}\right)=\dfrac{2^{x_{1}}-1}{2^{x_{1}+1}}-\dfrac{2^{x_{2}}-1}{2^{x_{2}+1}}\)
\(=\dfrac{\left(2^{x_{1}}-1\right)\left(2^{x_{2}}+1\right)-\left(2^{x_{2}}-1\right)\left(2^{x_{1}+1}\right)}{\left(2^{x_{1}+1}\right)\left(2^{x_{2}}+1\right)}=\dfrac{2\left(2^{x_{1}}-2^{x_{2}}\right)}{\left(2^{x_{1}+1}\right)\left(2^{x_{2}+1}\right)}\)
因为\(y=2^x\)是\(R\)上的增函数,且\(x_1<x_2\),所以\(\left(2^{x_{1}}-2^{x_{2}}\right)<0\),
又 \(\left(2^{x_{1}}+1\right)\left(2^{x_{2}}+1\right)>0\),
所以\(f(x_1 )-f(x_2 )<0\),即\(f(x_1 )<f(x_2 )\),
所以\(f(x)\)在\(R\)上是增函数;
(3) \(f(x)=\dfrac{2^{x}-1}{2^{x}+1}=\dfrac{2^{x}+1-2}{2^{x}+1}=1-\dfrac{2}{2^{x}+1}\),
由\(2^x>0\),得\(2^x+1>1\),所以 \(0<\dfrac{2}{2^{x}+1}<2\),
所以 \(-1<1-\dfrac{2}{2^{x}+1}<1\),即\(-1<f(x)<1\),
所以函数\(f(x)\)的值域为\((-1,1)\).
【C组---拓展题】
1.函数 \(f(x)=\dfrac{x^{3}}{2^{-x}-2^{x}}\)的图象大致为( )
A. \(\qquad \qquad\) B.
\(\qquad \qquad\) B. 
C. \(\qquad \qquad\) D.
\(\qquad \qquad\) D.
2.若函数\(F(x)=f(x)-2x^4\)是奇函数, \(G(x)=f(x)+\left(\dfrac{1}{2}\right)^{x}\)为偶函数,则\(f(-1)=\) \(\underline{\quad \quad}\) .
3.已知函数\(f(x)=x|x|+4x+1,x∈R\),若\(f(a)+f(a^2-1)<2\),则实数\(a\)的取值范围\(\underline{\quad \quad}\).
4.若函数\(f(x)\)的定义域是\(R\),且对任意\(x,y∈R\),都有\(f(x+y)=f(x)+f(y)\)成立.试判断\(f(x)\)的奇偶性.
参考答案
- 答案 \(B\)
解析 函数的定义域为\(\{x|x≠0\}\)关于原点对称,且 \(f(-x)=\dfrac{-x^{3}}{2^{x}-2^{-x}}=\dfrac{x^{3}}{2^{-x}-2^{x}}=f(x)\),
(或由\(y=x^3,y=2^{-x}-2^x\)均是奇函数,得 \(f(x)=\dfrac{x^{3}}{2^{-x}-2^{x}}\)是偶函数)
即函数\(f(x)\)为偶函数,其图象关于\(y\)轴对称,可排除\(CD\);
又 \(f(1)=\dfrac{1}{2^{-1}-2}=-\dfrac{2}{3}<0\),可排除\(A\);
故选:\(B\). - 答案 \(\dfrac{5}{4}\)
解析 \(∵\)函数\(F(x)=f(x)-2x^4\)是奇函数,
\(∴F(1)+F(-1)=0\),即\(f(1)-2+f(-1)-2=0\),则\(f(1)+f(-1)=4\) ①,
\(\because G(x)=f(x)+\left(\dfrac{1}{2}\right)^{x}\)为偶函数,
\(∴G(1)=G(-1)\),即 \(f(1)+\dfrac{1}{2}=f(-1)+2\),则 \(f(1)-f(-1)=\dfrac{3}{2}\) ②,
由①-②解得 \(f(-1)=\dfrac{4-\dfrac{3}{2}}{2}=\dfrac{5}{4}\). - 答案 \(\left(\dfrac{-1-\sqrt{5}}{2}, \dfrac{-1+\sqrt{5}}{2}\right)\)
解析 设\(g(x)=x|x|+4x\),\(x∈R\),则 \(g(x)=\left\{\begin{array}{l} -x^{2}+4 x, x \leq 0 \\ x^{2}+4 x, x>0 \end{array}\right.\),
又\(g(-x)=(-x)|-x|+4(-x)=-(x|x|+4x)=-g(x)\),
\(∴g(x)\)为\(R\)上的奇函数,且为增函数;
由\(f(x)=g(x)+1\),
\(∴\)不等式\(f(a)+f(a^2-1)<2\)可化为\(g(a)+g(a^2-1)<0\),
即\(g(a^2-1)<-g(a)\),\(∴g(a^2-1)<g(-a)\),
\(∴a^2-1<-a\),即\(a^2+a-1<0\),解得 \(\dfrac{-1-\sqrt{5}}{2}<a<\dfrac{-1+\sqrt{5}}{2}\).
\(∴a\)的取值范围是\(\left(\dfrac{-1-\sqrt{5}}{2}, \dfrac{-1+\sqrt{5}}{2}\right)\). - 答案 奇函数
解析 在\(f(x+y)=f(x)+f(y)\)中,
令\(x=y=0\),得\(f(0+0)=f(0)+f(0)\),\(∴f(0)=0\).
再令\(y=-x\),则\(f(x-x)=f(x)+f(-x)\),即\(f(x)+f(-x)=0\),
\(∴f(-x)=-f(x)\),故\(f(x)\)为奇函数.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号