2.3.3 点到直线的距离公式 2.3.4 两条平行直线间的距离
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
【基础过关系列】2022-2023学年高二数学上学期同步知识点剖析精品讲义(人教A版2019)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
选择性必修第一册同步巩固,难度2颗星!
基础知识
点到直线的距离公式
点\(P_0 (x_0 ,y_0)\)到直线\(l:A x+B y+C=0\)的距离 \(d=\dfrac{\left|A x_{0}+B y_{0}+C\right|}{\sqrt{A^{2}+B^{2}}}\).
证明 过点\(P\)作\(PQ⊥l\)交直线\(l\)与\(Q\),
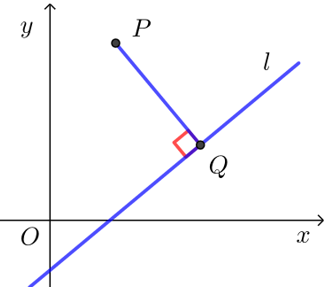
设\(A≠0\),\(B≠0\),由\(PQ⊥l\),以及直线\(l\)的斜率为 \(-\dfrac{A}{B}\),可得l的垂线\(PQ\)的斜率为 \(\dfrac{B}{A}\),
因此,垂线\(PQ\)的方程为 \(y-y_{0}=\dfrac{B}{A}\left(x-x_{0}\right)\),即\(Bx-Ay=Bx_0-Ay_0\),
解方程组 \(\left\{\begin{array}{l}
A x+B y+C=0 \\
B x-A y=B x_{0}-A y_{0}
\end{array}\right.\)
得直线\(l\)与\(PQ\)的交点坐标,即垂足\(Q\)的坐标为 \(\left(\dfrac{B^{2} x_{0}-A B y_{0}-A C}{A^{2}+B^{2}}, \dfrac{-A B x_{0}+A^{2} y_{0}-B C}{A^{2}+B^{2}}\right)\),
于是 \(|P Q|=\sqrt{\left(\dfrac{B^{2} x_{0}-A B y_{0}-A C}{A^{2}+B^{2}}-x_{0}\right)^{2}+\left(\dfrac{-A B x_{0}+A^{2} y_{0}-B C}{A^{2}+B^{2}}-y_{0}\right)^{2}}\)
\(=\sqrt{\dfrac{\left(A x_{0}+B y_{0}+C\right)^{2}}{A^{2}+B^{2}}}=\dfrac{\left|A x_{0}+B y_{0}+C\right|}{\sqrt{A^{2}+B^{2}}}\)
因此点\(P_0 (x_0 ,y_0)\)到直线\(l:A x+B y+C=0\)的距离 \(d=\dfrac{\left|A x_{0}+B y_{0}+C\right|}{\sqrt{A^{2}+B^{2}}}\).
当\(A=0\)或\(B=0\)时,上述公式仍然成立.
(也可以用向量的方法证明)
【例】 点\(P(1,2)\)到直线\(3x+4y-12=0\)的距离为 \(\underline{\quad \quad}\) .
解析 由点到直线的距离公式得 \(d=\dfrac{|3+8-12|}{\sqrt{3^{2}+4^{4}}}=\dfrac{1}{5}\).
两平行直线间的距离
两条平行线\(Ax+B y+C_1=0\)与\(A x+B y+C_2=0\)间的距离 \(d=\dfrac{\left|C_{1}-C_{2}\right|}{\sqrt{A^{2}+B^{2}}}\).
证明 在直线\(Ax+B y+C_1=0\)上任取一点\(P(x_0,y_0 )\),点\(P(x_0,y_0 )\)到直线\(A x+B y+C_2=0\)的距离就是两平行线的距离,
即 \(d=\dfrac{\left|A x_{0}+B y_{0}+C_{2}\right|}{\sqrt{A^{2}+B^{2}}}\),
因为点\(P(x_0,y_0 )\)在直线\(Ax+B y+C_1=0\)上,所以\(Ax_0+By_0+C_1=0\),
即\(Ax_0+By_0=-C_1\),
因此 \(d=\dfrac{\left|A x_{0}+B y_{0}+C_{2}\right|}{\sqrt{A^{2}+B^{2}}}=\dfrac{\left|-C_{1}+C_{2}\right|}{\sqrt{A^{2}+B^{2}}}=\dfrac{\left|C_{1}-C_{2}\right|}{\sqrt{A^{2}+B^{2}}}\).
【例】 两平行线\(3x-2y-15=0\)与\(3x-2y+11=0\)的距离为 \(\underline{\quad \quad}\) .
解析 由两平行直线距离公式得 \(d=\dfrac{|11-(-15)|}{\sqrt{9+4}}=2 \sqrt{13}\).
基本方法
【题型1】 点到直线的距离
【典题1】求过点\(P(0,2)\)且与点\(A(1,1)\),\(B(-3,1)\)等距离的直线\(l\)的方程.
解析 方法一
由于点\(A(1,1)\)与\(B(-3,1)\)到\(y\)轴的距离不相等,所以直线\(l\)的斜率存在,设为\(k\),
又因为直线\(l\)在\(y\)轴上的截距为\(2\),
则直线\(l\)的方程为\(y=kx+2\),即\(kx-y+2=0\).
由点\(A(1,1)\)与\(B(-3,1)\)到直线\(l\)的距离相等,
得 \(\dfrac{|k-1+2|}{\sqrt{k^{2}+1}}=\dfrac{|k \times(-3)-1+2|}{\sqrt{k^{2}+1}}\),解得\(k=0\)或\(k=1\).
\(∴\)直线\(l\)的方程是\(y=2\)或\(x-y+2=0\).
方法二
当直线\(l\)过\(AB\)的中点时,直线\(l\)与点\(A\),\(B\)等距离,
\(∵AB\)的中点是\((-1,1)\),又直线\(l\)过点\(P(0,2)\),
\(∴\)直线\(l\)的方程是\(x-y+2=0\);
当直线\(l∥AB\)时,直线\(l\)与点\(A\),\(B\)等距离,
\(∵\)直线\(AB\)的斜率为\(0\),\(∴\)直线\(l\)的斜率为\(0\).故方程为\(y=2\).
综上所述,满足条件的直线\(l\)的方程是\(x-y+2=0\)或\(y=2\).
【典题2】求点\(P(\cosθ,\sinθ)\)到直线\(3x+4y-12=0\)的距离的取值范围.
解析 记\(d\)为点 \(P(\cosθ,\sinθ)\)到直线\(3x+4y-12=0\)的距离,
即: \(d=\dfrac{1}{5}|3 \cos \theta+4 \sin \theta-12|=\dfrac{1}{5}|5 \sin (\theta+\varphi)-12|\),其中 \(\tan \varphi=\dfrac{3}{4}\);
当\(θ\)变化时,\(d\)的最大值为 \(\dfrac{17}{5}\),\(d\)的最小值为 \(\dfrac{ 7}{5}\),
【典题3】如图,在\(△ABC\)中, \(BC\)边上的高所在的直线方程为\(x-2y+1=0\),\(∠A\)的平分线所在的直线方程为\(y=0\),若点\(B\)的 坐标为\((1,2)\),求:
(1)点\(A\)和点\(C\)的坐标;(2)求\(△ABC\)的面积.

解析 (1)由 \(\left\{\begin{array}{l}
x-2 y+1=0 \\
y=0
\end{array}\right.\),得顶点\(A(-1,0)\).
又\(AB\)的斜率 \(k_{A B}=\dfrac{2-0}{1-(-1)}=1\).
\(∵x\)轴是\(∠A\)的平分线,
故\(AC\)的斜率为\(-1\),\(AC\)所在直线的方程为\(y=-(x+1)\)①,
已知\(BC\)上的高所在直线的方程为\(x-2y+1=0\),
故\(BC\)的斜率为\(-2\),\(BC\)所在的直线方程为\(y-2=-2(x-1)\)②,
解①,②得顶点\(C\)的坐标为\((5,-6)\);
(2) \(|B C|=\sqrt{(1-5)^{2}+(2+6)^{2}}=4 \sqrt{5}\),
又直线\(BC\)的方程是\(2x+y-4=0\),\(A\)到直线的距离 \(d=\dfrac{|-2-4|}{\sqrt{5}}=\dfrac{6}{\sqrt{5}}\).
\(△ABC\)的面积 \(S=\dfrac{1}{2}|B C| \cdot d=\dfrac{1}{2} \times 4 \sqrt{5} \times \dfrac{6}{\sqrt{5}}=12\).
巩固练习
1.已知\(A(-3,-2)\),\(B(-1,4)\)到直线\(l:x+ay+1=0\)的距离相等,则实数\(a\)为\(\underline{\quad \quad}\).
2.求过点\(A(-1,2)\)且到原点的距离等于 \(\dfrac{\sqrt{2}}{2}\)的直线方程.
3.已知直线\(l\)经过点\(P(5,10)\),且原点到它的距离为\(5\),求直线\(l\)的方程.
参考答案
- 答案 \(1\)或 \(-\dfrac{1}{3}\)
解析 因为点\(A(-3,-2)\),\(B(-1,4)\)到直线\(l:x+ay+1=0\)的距离相等,
所以 \(\dfrac{|-3-2 a+1|}{\sqrt{1+a^{2}}}=\dfrac{|-1+4 a+1|}{\sqrt{1+a^{2}}}\),解得\(a=1\)或 \(a=-\dfrac{1}{3}\). - 答案 \(x+y-1=0\)或\(7x+y+5=0\)
解析 显然直线\(x=-1\)到原点的距离为\(1\),所以所求直线的斜率是存在的.
设所求直线的方程为\(y-2=k(x+1)\),化成一般式为\(kx-y+2+k=0\).
由题意得 \(\dfrac{|2+k|}{\sqrt{k^{2}+1}}=\dfrac{\sqrt{2}}{2}\),解得\(k=-1\)或\(-7\).
故适合题意的直线方程为\(y-2=-(x+1)\)或\(y-2=-7(x+1)\),
即\(x+y-1=0\)或\(7x+y+5=0\). - 答案 \(3x-4y+25=0\)
解析 当直线斜率不存在时直线方程为\(x=5\),满足原点到它的距离为\(5\),
当斜率存在时,设直线为\(y-10=k(x-5)\),
变形为\(kx-y+10-5k=0\),
\(\therefore d=\dfrac{|10-5 k|}{\sqrt{k^{2}+1}}=5 \Rightarrow k=\dfrac{3}{4}\),
所以直线方程为\(3x-4y+25=0\).
【题型2】两平行直线间的距离
【典题1】 求与直线\(3x-4y-2=0\)平行且距离为\(2\)的直线方程.
解析 \(∵\)所求直线与直线\(3x-4y-2=0\)平行,
\(∴\)设所求直线方程为\(3x-4y+C=0\).
由两平行直线间的距离公式得 \(\dfrac{|C+2|}{\sqrt{3^{2}+(-4)^{2}}}=2\),即\(|C+2|=10\).\(∴C=8\)或\(-12\).
\(∴\)所求直线方程为\(3x-4y+8=0\)或\(3x-4y-12=0\).
巩固练习
1.已知直\(线l_1:x+y-1=0\),\(l_2:x+y+a=0\),且两直线间的距离为 \(\sqrt{2}\),则\(a=\)\(\underline{\quad \quad}\).
2.直线\(l_1\)过点\(A(0,1)\),\(l_2\)过点\(B(5,0)\),如果\(l_1∥l_2\)且\(l_1\)与\(l_2\)的距离为\(5\),求直线\(l_1\)与\(l_2\)的方程.
参考答案
- 答案 \(-3\)或\(1\)
解析 由 \(d=\dfrac{|a-(-1)|}{\sqrt{1+1}}=\sqrt{2}\)解得\(a=-3\)或\(1\). - 答案 直线\(l_1\)与\(l_2\)的方程分别为\(12x-5y+5=0\),\(12x-5y-60=0\).
解析 当\(l_1\),\(l_2\)的斜率不存在时,即l_1:x=0,l_2:x=5时,满足条 件.
当\(l_1\),\(l_2\)的斜率存在时,
设\(l_1:y=kx+1\),即\(kx-y+1=0\),\(l_2:y=k(x-5)\),即\(kx-y-5k=0\),
由两条平行直线间的距离公式得 \(\dfrac{|1-(-5 k)|}{\sqrt{k^{2}+(-1)^{2}}}=5\),解得 \(k=\dfrac{12}{5}\).
此时\(l_1:12x-5y+5=0\),\(l_2:12x-5y-60=0\).
综上所述,\(l_1\),\(l_2\)斜率不存在时,直线\(l_1\)与\(l_2\)的方程分别为\(x=0\),\(x=5\);
\(l_1\),\(l_2\)斜率存在时,直线\(l_1\)与\(l_2\)的方程分别为\(12x-5y+5=0\),\(12x-5y-60=0\).
【题型3】 最值问题
【典题1】 已知点\(P(1,2)\),则当点\(P\)到直线\(2ax+y-4=0\)的距离最大时,\(a=\)( )
A.\(1\) \(\qquad \qquad\) B. \(-\dfrac{1}{4}\) \(\qquad \qquad\) C. \(\dfrac{1}{4}\) \(\qquad \qquad\) D. \(\sqrt{5}\)
解析 因为直线\(2ax+y-4=0\)恒过定点\(A(0,4)\),
故当\(PA\)与直线垂直时,点\(P\)到直线的距离达到最大值,
此时过\(P,A\)的直线的斜率为\(-2\),
所以直线$2ax+y-4=$0的斜率为 \(\dfrac{1}{2}\),
故\(a= -\dfrac{1}{4}\).
故选:\(B\).
【典题2】已知点\(M(a,b)\)在直线\(l:3x+4y=25\)上,则 \(\sqrt{a^{2}+b^{2}}\)的最小值为\(\underline{\quad \quad}\).
解析 \(∵ \sqrt{a^{2}+b^{2}}\)的几何意义是点\(O(0,0)\)到点\(M\)的距离,又点\(M\)在直线l上,
\(∴ \sqrt{a^{2}+b^{2}}\)的最小值为点\(O\)到直线\(l\)的距离\(d\),
又 \(d=\dfrac{25}{\sqrt{3^{2}+4^{2}}}=5\),
\(\therefore\left(\sqrt{a^{2}+b^{2}}\right)_{\min }=5\),
故答案为:\(5\).
巩固练习
1.点\(P\)在直线\(x+y-4=0\)上,\(O\)为原点,则\(|OP|\)的最小值为\(\underline{\quad \quad}\).
2.已知点\(P(-2,2)\),直线\(l:(λ+2)x-(λ+1)y-4λ-6=0\),则点\(P\)到直线\(l\)的距离的取值范围为\(\underline{\quad \quad}\).
3.分别过点\(A(1,3)\)和点\(B(2,4)\)的直线\(l_1\)和\(l_2\)互相平行且有最大距离,则\(l_1\)的方程是\(\underline{\quad \quad}\).
4.若点\((m,n)\)在直线\(l:3x+4y-13=0\)上,则 \((m-1)^{2}+n^{2}\)的最小值为( )
A.\(3\) \(\qquad \qquad\) B.\(4\) \(\qquad \qquad\) C.\(2\) \(\qquad \qquad\) D.\(6\)
参考答案
-
答案 \(2 \sqrt{2}\)
解析 当\(OP\)与直线\(x+y-4=0\)垂直时,\(|OP|\)最小,
\(∴|OP|\)的最小值就是原点\(O\)到直线\(x+y-4=0\)的距离,
\(\therefore|O P|_{\min }=\dfrac{4}{\sqrt{2}}=2 \sqrt{2}\). -
答案 \([0,4 \sqrt{2})\)
解析 \(∵\)直线\(l:(λ+2)x-(λ+1)y-4λ-6=0\),即\(λ⋅(x-y-4)+2x-y-6=0\),
该直线经过\(x-y-4=0\)和\(2x-y-6=0\)的交点\(M(2,-2)\),
当点\(P(-2,2)\)在直线\(l:(λ+2)x-(λ+1)y-4λ-6=0\)上,点\(P\)到直线\(l\)的距离最小为\(0\);
当\(PM\)和直线\(l\)垂直时,点\(P\)到直线\(l\)的距离最大为 \(P M=\sqrt{(-2-2)^{2}+(2+2)^{2}}=4 \sqrt{2}\),
此时,直线\(l\)的方程为:\(x-y-4=0\),不存在\(λ\)值,满足此条件,
故点\(P\)到直线\(l\)的距离最大\(PM\)取不到,
故点\(P\)到直线\(l\)的距离的取值范围为 \([0,4 \sqrt{2})\),
故答案为: \([0,4 \sqrt{2})\). -
答案 \(x+y-4=0\)
解析 \(∵\)分别过点\(A(1,3)\)和点\(B(2,4)\)的直线\(l_1\)和\(l_2\)互相平行且有最大距离,
故此最大距离为 \(|A B|=\sqrt{2}\), \(\because k_{A B}=\dfrac{4-3}{2-1}=1\),
故\(l_1\)的斜率为 \(-\dfrac{1}{k_{A B}}=-1\),
故\(l_1\)的方程为\(y-3=-1(x-1)\),即\(x+y-4=0\),
故答案为:\(x+y-4=0\). -
答案 \(B\)
解析 \(\sqrt{(m-1)^{2}+n^{2}}\)表示点\((1,0)\)与点\((m,n)\)的距离,
则 \(\sqrt{(m-1)^{2}+n^{2}}\)的最小值为点\((1,0)\)到直线\(3x+4y-13=0\)的距离,
即 \(\dfrac{|3-13|}{\sqrt{3^{2}+4^{2}}}=2\),
故 \((m-1)^{2}+n^{2}\)的最小值为\(4\).
故选:\(B\).
分层练习
【A组---基础题】
1.已知点\((a,2)(a>0)\)到直线\(l:x-y+3=0\)的距离为\(1\),则\(a\)为( )
A. \(\sqrt{2}\) \(\qquad \qquad\) B.\(2-\sqrt{2}\) \(\qquad \qquad\) C.\(\sqrt{2}-1\) \(\qquad \qquad\) D.\(\sqrt{2}+1\)
2.已知直线\(l\)过点\(P(3,3)\)且与点\(A(-2,2)\)、\(B(4,-2)\)等距离,则直线\(l\)的方程为( )
A.\(3x-2y-3=0\)或\(2x+3y-15=0\) \(\qquad \qquad\) B.\(2x-3y+3=0\)或\(3x-2y-3=0\)
C.\(2x-3y+3=0\)或\(2x+3y-15=0\) \(\qquad \qquad\) D.\(2x+3y-15=0\)或\(2x+3y-2=0\)
3.过点\(P(0,1)\),且与点\(A(3,3)\)和\(B(5,-1)\)的距离相等的直线方程是( )
A.\(y=1\) \(\qquad \qquad \qquad \qquad \qquad\) B.\(2x+y-1=0\) \(\qquad \qquad\)
C.\(y=1\)或\(2x+y-1=0\) \(\qquad \qquad\) D.\(2x+y-1=0\)或\(2x+y+1=0\)
4.直线\(x+y-1=0\)与直线\(x-2y-4=0\)交于点\(P\),则点\(P\)到直线\(kx-y+1+2k=0(k∈R)\)的最大距离为( )
A. \(\sqrt{2}\) \(\qquad \qquad\) B.\(2\) \(\qquad \qquad\) C. \(2 \sqrt{5}\) \(\qquad \qquad\) D.\(4\)
5.在平面直角坐标系\(xOy\)中,坐标原点\(O\)到直线 \(x \cos \theta+y \sin \theta+1=0\)的距离为\(\underline{\quad \quad}\).
6.已知实数\(x,y\)满足\(2x+y+3=0\),则 \(\sqrt{x^{2}+y^{2}+2 x+1}\)的最小值为\(\underline{\quad \quad}\).
7.若直线\(m\)被两平行线 \(l_{1}: x-\sqrt{3} y+1=0\)与 \(l_{2}: x-\sqrt{3} y+3=0\)所截得的线段的长为\(1\),则直线\(m\)的倾斜角的大小为\(\underline{\quad \quad}\).
8.已知两条平行直线\(L_1:x+2y+3=0\),\(L_2:3x+by+c=0\)间的距离为 \(\sqrt{5}\),则\(b+c=\)\(\underline{\quad \quad}\).
9.求垂直于直线 \(x-\sqrt{3} y+1=0\)且到原点的距离等于\(5\)的直线方程.
10.已知\(△ABC\)的三个顶点\(A(3,7)\),\(B(-2,5)\),\(C(-3,-5)\),点\(D\)为\(AC\)的中点.
(1)求点\(D\)的坐标;(2)求直线\(BD\)的方程.(3)求\(△ABD\)的面积.
参考答案
-
答案 \(C\)
解析 由 \(d=\dfrac{|a-2+3|}{\sqrt{1+1}}=1\)解得\(a=\sqrt{2}-1\),故选\(C\). -
答案 \(A\)
解析 直线\(l\)过点\(P(3,3)\)且与点\(A(-2,2)\)、\(B(4,-2)\)等距离,
故直线\(l\)的斜率存在,设为\(k\),
则直线\(l\)的方程为 \(y-3=k(x-3)\),即\(kx-y+3-3k=0\),
根据 \(\dfrac{|-2 k-2+3-3 k|}{\sqrt{k^{2}+1}}=\dfrac{|4 k+2+3-3 k|}{\sqrt{k^{2}+1}}\),求得 \(k=\dfrac{3}{2}\),或 \(k=-\dfrac{2}{3}\),
故直线l的方程为\(3x-2y-3=0\)或\(2x+3y-15=0\),
故选:\(A\). -
答案 \(C\)
解析 当直线平行于直线\(AB\)时,或过\(AB\)的中点时满足题意,
当直线平行于直线\(AB\)时,所求直线的斜率为 \(k=\dfrac{3+1}{3-5}=-2\),
故直线方程为\(y=-2x+1\),即\(2x+y-1=0\);
当直线过\(AB\)的中点\((4,1)\)时,斜率为\(k=0\),
故直线方程为\(y=1\);
故所求直线方程是为:\(y=1\)或\(2x+y-1=0\).
故选:\(C\). -
答案 \(C\)
解析 \(\left\{\begin{array}{l} x+y-1=0 \\ x-2 y-4=0 \end{array}\right.\),解得 \(\left\{\begin{array}{l} x=2 \\ y=-1 \end{array}\right.\),
所以点\(P\)的坐标为\((2,-1)\),
而直线\(kx-y+1+2k=0\),即\(k(x+2)+1-y=0\),恒过点\(Q(-2,1)\),
点\(P\)到直线\(kx-y+1+2k=0\)的距离最大值为
\(P Q=\sqrt{[2-(-2)]^{2}+(-1-1)^{2}}=2 \sqrt{5}\),
故选:\(C\). -
答案 \(1\)
解析 坐标原点\(O\)到直线 \(x \cos \theta+y \sin \theta+1=0\)的距离为 \(\dfrac{|0+0+1|}{\sqrt{\cos ^{2} \theta+\sin ^{2} \theta}}=1\). -
答案 \(\dfrac{\sqrt{5}}{5}\)
解析 \(\sqrt{x^{2}+y^{2}+2 x+1}=\sqrt{(x+1)^{2}+y^{2}}\),
可看成点\(P(x,y)\)与点\(A(-1,0)\)之间的距离的最小值,
点\(A(-1,0)\)到直线\(2x+y+3=0\)的距离为 \(d=\dfrac{|2 \times(-1)+0+3|}{\sqrt{2^{2}+1^{2}}}=\dfrac{\sqrt{5}}{5}\),
故 \(\sqrt{x^{2}+y^{2}+2 x+1}\)的最小值为 \(\dfrac{\sqrt{5}}{5}\). -
答案 \(120°\)
解析 由两平行线间的距离为 \(\dfrac{|1-3|}{\sqrt{1+3}}=1\),
直线\(m\)被两平行线 \(l_{1}: x-\sqrt{3} y+1=0\)与 \(l_{2}: x-\sqrt{3} y+3=0\)所截得的线段的长为\(1\),
可得直线\(m\)和两平行线的夹角为\(90°\).
由于两条平行线的倾斜角为\(30°\),故直线m的倾斜角为\(120°\). -
答案 \(0\)或\(30\)
解析 因为两条平行直线\(L_1:x+2y+3=0\),\(L_2:3x+by+c=0\)间的距离为 \(\sqrt{5}\),
所以\(b=6\),且 \(\dfrac{|9-c|}{\sqrt{3^{2}+6^{2}}}=\sqrt{5}\),解得\(c=-6\)或\(24\),
所以\(b+c=0\)或\(30\). -
答案 \(\sqrt{3}x+y+10=0\)或\(\sqrt{3}x+y-10=0\)
解析 \(∵\)所求直线与直线\(x-\sqrt{3}y+1=0\)垂直,
\(∴\)设所求直线方程为\(\sqrt{3} x+y+C=0\).
则 \(\dfrac{|C|}{2}=5\),\(C=±10\).
\(∴\)所求 直线方程为\(\sqrt{3} x+y+10=0\)或\(\sqrt{3} x+y-10=0\). -
答案 (1) \((0,1)\) (2) \(2x+y-1=0\) (3) \(12\)
解析 (1)设\(D(x,y)\),
则 \(x=\dfrac{3+(-3)}{2}=0\), \(y=\dfrac{7+(-5)}{2}=1\),
\(∴\)点\(D\)的坐标为\((0,1)\).
(2)\(∵\)直线\(BD\)的斜率为 \(k=\dfrac{5-1}{-2-0}=-2\).
\(∴\)直线\(BD\)的方程为:\(y-1=-2(x-0)\),即\(2x+y-1=0\).
(3) \(\because|B D|=\sqrt{(-2-0)^{2}+(5-1)^{2}}=2 \sqrt{5}\),
\(∴A\)到直线\(BD\)的距离为 \(d=\dfrac{|2 \times 3+7-1|}{\sqrt{2^{2}+1^{2}}}=\dfrac{12 \sqrt{5}}{5}\)
\(∴△ABD\)的面积为 \(S_{\triangle A B D}=\dfrac{1}{2}|B D| d=\dfrac{1}{2} \times 2 \sqrt{5} \times \dfrac{12 \sqrt{5}}{5}=12\).
【B组---提高题】
1.点 \(P(\sin \theta, \sqrt{3} \cos \theta)\)到直线\(x+y+8=0\)的距离的最小值为( )
A.\(4\) \(\qquad \qquad\) B. \(2 \sqrt{3}\) \(\qquad \qquad\) C. \(3 \sqrt{2}\) \(\qquad \qquad\) D.\(5 \sqrt{2}\)
2.在直角坐标系\(xOy\)中,已知直线 \(l: x \cos \theta+y \sin \theta=1\),当\(θ\)变化时,动直线始终没有经过点\(P\).定点\(Q\)的坐标\((-2,0)\),则\(|PQ|\)的取值范围为( )
A.\([0,2]\) \(\qquad \qquad\) B.\((0,2)\) \(\qquad \qquad\) C.\([1,3]\) \(\qquad \qquad\) D.\((1,3)\)
3.平面直角坐标系内,动点\(P(a,b)\)到直线 \(l_{1}: y=\dfrac{1}{2} x\)和\(l_2:y=-2x\)的距离之和是\(4\),则\(a^2+b^2\)的最小值是( )
A.\(12\) \(\qquad \qquad\) B.\(2\) \(\qquad \qquad\) C.\(8\) \(\qquad \qquad\) D.\(4\)
4.平面直角坐标系内,动点\(P(a,b)\)到直线\(l_1\)已知三条直线\(l_1:2x-y+a=0(a>0)\),\(l_2:-4x+2y+1=0\),\(l_3:x+y-1=0\),且\(l_1\)与\(l_2\)间的距离是 \(\dfrac{7 \sqrt{5}}{10}\).
(1)求\(a\)的值.
(2)能否找到一点\(P\),使\(P\)同时满足下列三个条件?若能,求点\(P\)的坐标;若不能,说明理由.
①点\(P\)在第一象限;
②点\(P\)到\(l_1\)的距离是点\(P\)到\(l_2\)的距离的 \(\dfrac{1}{2}\);
③点\(P\)到\(l_1\)的距离与点\(P\)到\(l_3\)的距离之比是 \(\sqrt{2}: \sqrt{5}\).
参考答案
- 答案 \(C\)
解析 点 \(P(\sin \theta, \sqrt{3} \cos \theta)\)到直线\(x+y+8=0\)的距离为
\(d=\dfrac{|\sin \theta+\sqrt{3} \cos \theta+8|}{\sqrt{1+1}}=\dfrac{2 \sin \left(\theta+\dfrac{\pi}{3}\right)+8}{\sqrt{2}} \geq \dfrac{-2+8}{\sqrt{2}}=3 \sqrt{2}\).
所以当 \(\sin \left(\theta+\dfrac{\pi}{3}\right)=-1\),即 \(\theta=2 k \pi+\dfrac{7 \pi}{6}\),\(k∈Z\)时,\(d\)取得最小值为 \(3 \sqrt{2}\).
故选:\(C\). - 答案 \(D\)
解析 由题意知,点\(P\)坐标不确定,
当\(θ=0\)时,直线\(l: x \cos \theta+y \sin \theta=1\)化为\(x=1\),直线\(l\)上的点\(A(1,0)\)到点\(Q\)的距离为\(3\),
可以排除选项\(C\);
当\(θ=π\)时,直线 \(l: x \cos \theta+y \sin \theta=1\)化为\(x=-1\),直线\(l\)上的点\(B(-1,0)\)点\(Q\)的距离为\(1\),
可以排除选项\(A、B、C\);
所以\(|PQ|\)的取值范围是\((1,3)\).
故选:\(D\). - 答案 \(C\)
解析 设动点\(P(a,b)\)到直线 \(l_{1}: y=\dfrac{1}{2} x\)的距离为\(m\),到直线\(l_2:y=-2x\)的距离为\(n\),
\(∵l_{1}: y=\dfrac{1}{2} x\)和\(l_2:y=-2x\)的距离之和是\(4\),\(∴m+n=4\),
\(\because m^{2}+n^{2} \geq 2 m n\), \(\therefore 2\left(m^{2}+n^{2}\right) \geq(m+n)^{2}=16\),
\(\therefore m^{2}+n^{2} \geq 8\),
\(∵\)直线 \(l_{1}: y=\dfrac{1}{2} x\)和\(l_2:y=-2x\)垂直且过原点,
\(\therefore a^{2}+b^{2}=m^{2}+n^{2} \geq 8\),
\(∴a^{2}+b^{2}\)的最小值是\(8\).
故选:\(C\). - 答案 (1)\(a=3\) (2) \(P\left(\dfrac{1}{9}, \dfrac{37}{18}\right)\)
解析 (1)将直线\(l_2\)的方程化为 \(2 x-y-\dfrac{1}{2}=0\),
\(∴\)两条平行线\(l_1\)与\(l_2\)间的距离 \(d=\dfrac{\left|a-\left(-\dfrac{1}{2}\right)\right|}{\sqrt{2^{2}+(-1)^{2}}}=\dfrac{7 \sqrt{5}}{10}\),
由\(a>0\),解得\(a=3\).
(2)假设存在点\(P\),设点\(P(x_0,y_0 )\).
若\(P\)点满足条件②,则P点在与\(l_1\),\(l_2\)平行的直线\(l':2x-y+c=0\)上,
且 \(\dfrac{|c-3|}{\sqrt{5}}=\dfrac{1}{2} \cdot \dfrac{\left|c+\dfrac{1}{2}\right|}{\sqrt{5}}\),解得 \(c=\dfrac{13}{2}\)或 \(C=\dfrac{11}{6}\),
所以 \(2 x_{0}-y_{0}+\dfrac{13}{2}=0\)或 \(2 x_{0}-y_{0}+\dfrac{11}{6}=0\).
若\(P\)点满足条件③,由点到直线的距离公式,
有 \(\dfrac{\left|2 x_{0}-y_{0}+3\right|}{\sqrt{5}}=\dfrac{\sqrt{2}}{\sqrt{5}} \cdot \dfrac{\left|x_{0}+y_{0}-1\right|}{\sqrt{2}}\),
即\(|2x_0-y_0+3|=|x_0+y_0-1|\),
所以\(x_0-2y_0+4=0\)或\(3x_0+2=0\).
由于点\(P\)在第一象限,所以排除\(3x_0+2=0\).
联立方程 \(2 x_{0}-y_{0}+\dfrac{13}{2}=0\)和\(x_0-2y_0+4=0\),
解得 \(\left\{\begin{array}{l} x_{0}=-3 \\ y_{0}=\dfrac{1}{2} \end{array}\right.\)(舍去);
联立方程 \(2 x_{0}-y_{0}+\dfrac{11}{6}=0\)和\(x_0-2y_0+4=0\),
解得 \(\left\{\begin{array}{l} x_{0}=\dfrac{1}{9} \\ y_{0}=\dfrac{37}{18} \end{array}\right.\),
所以存在点 \(P\left(\dfrac{1}{9}, \dfrac{37}{18}\right)\)同时满足三个条件.
【C组---拓展题】
1.在平面直角坐标系中,动点\(P\)到两条直线\(3x-y=0\)与\(x+3y=0\)的距离之和等于\(4\),则点 \(P\)到原点距离的取值范围为\(\underline{\quad \quad}\).
2.设\(a,b,c\)是三角形的三边长,直线\(l:ax+by+c=0\),\(M(-1,-1)\),\(N(-1,1)\),\(P(1,1)\),\(Q(1,-1)\).
(1)判断点\(M,N,P,Q\)是否均在直线的同一侧,请说明理由;
(2)设\(M,N,P,Q\)到直线的距离和为\(S\),求证: \(2 \sqrt{2}<S<4 \sqrt{2}\).
参考答案
-
答案 [2√2,4]
解析 \(∵3x-y=0\)与\(x+3y=0\)的互相垂直,且交点为原点,
\(∴\)设\(P\)到直线的距离分别为\(a\),\(b\),则\(a⩾0\),\(b⩾0\),
则\(a+b=4\),即\(b=4-a⩾0\),
得\(0⩽a⩽4\),
由勾股定理可知 \(O P=\sqrt{a^{2}+b^{2}}=\sqrt{a^{2}+(4-a)^{2}}\)\(=\sqrt{2 a^{2}-8 a+16}=\sqrt{2(a-2)^{2}+8}\),
\(∵0⩽a⩽4\), \(\therefore|O P| \in[2 \sqrt{2}, 4]\).
故答案为 \([2 \sqrt{2}, 4]\).

-
答案 (1) 点\(N,P,Q\)在直线\(l\)的同侧,而点\(M\)在直线\(l\)的另一侧 (2) 略
解析 (1)解:令\(f(x,y)=ax+by+c\),
则\(f(-1,-1)=c-(a+b)\),\(f(-1,1)=(b+c)-a\),\(f(1,1)=a+b+c\),\(f(1,-1)=(a+c)-b>0\).
由三角形的性质可知:\(f(-1,-1)<0\),\(f(-1,1)>0\),\(f(1,1)>0\),\(f(1,-1)>0\),
点\(N,P,Q\)在直线\(l\)的同侧,而点\(M\)在直线\(l\)的另一侧.
(2)证明:\(M,N,P,Q\)到直线的距离和为
\(S=\dfrac{|c-(a+b)|}{\sqrt{a^{2}+b^{2}}}+\dfrac{|(b+c)-a|}{\sqrt{a^{2}+b^{2}}}+\dfrac{|a+b+c|}{\sqrt{a^{2}+b^{2}}}+\dfrac{|(a+c)-b|}{\sqrt{a^{2}+b^{2}}}\)\(=\dfrac{2(a+b+c)}{\sqrt{a^{2}+b^{2}}}\),
不妨设\(a⩾b\),\(a-b⩽c⩽a+b\).
\(\therefore \dfrac{a+b+c}{\sqrt{a^{2}+b^{2}}}>\dfrac{a+b+(a-b)}{\sqrt{a^{2}+b^{2}}}=\dfrac{2 a}{\sqrt{a^{2}+b^{2}}} \geqslant \dfrac{2 a}{\sqrt{2 a^{2}}}=\sqrt{2}\).
\(\dfrac{a+b+c}{\sqrt{a^{2}+b^{2}}}<\dfrac{a+b+a+b}{\sqrt{a^{2}+b^{2}}}=\dfrac{2(a+b)}{\sqrt{a^{2}+b^{2}}} \leqslant 2 \sqrt{2}\).
\(\therefore 2 \sqrt{2}<S<4 \sqrt{2}\).


 浙公网安备 33010602011771号
浙公网安备 33010602011771号