1.1.2 空间向量的数量积运算
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
【基础过关系列】 高二数学上学期同步知识点剖析精品讲义(人教A版2019)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
选择性必修第一册同步巩固,难度2颗星!
基础知识
空间向量的夹角及其表示
已知两非零向量\(\vec{a}, \vec{b}\),在空间任取一点\(O\),作\(\overrightarrow{O A}=\vec{a}, \overrightarrow{O B}=\vec{b}\),则\(\angle A O B\)叫做向量\(\vec{a}\)与\(\vec{b}\)的夹角,记作 \(\langle\vec{a}, \vec{b}\rangle\);且规定 \(0 \leq<\vec{a}, \vec{b}>\leq \pi\) ;
若 \(\langle\vec{a}, \vec{b}\rangle=\dfrac{\pi}{2}\),则称\(\vec{a}\)与\(\vec{b}\)互相垂直,记作: \(\vec{a} \perp \vec{b}\) .

向量的数量积
已知向量\(\vec{a}\) , \(\vec{b}\),则 \(|\vec{a}| \vec{b} \mid \cos <\vec{a}, \vec{b}>\)叫做\(\vec{a}, \vec{b}\)的数量积,记作 \(\vec{a} \cdot \vec{b}\),
即 \(\vec{a} \cdot \vec{b}=|\vec{a}| \vec{b} \mid \cos <\vec{a}, \vec{b}>\).
特别地,零向量与任何向量的数量积为\(0\).
【例】 如图,正方体\(ABCD-A'B'C'D'\)的棱长为\(1\),求 \(\overrightarrow{D^{\prime} A} \cdot \overrightarrow{D^{\prime} B^{\prime}}\), \(\overrightarrow{A D^{\prime}} \cdot \overrightarrow{B C}\).
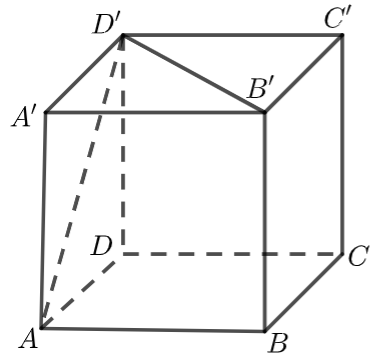
解析 \(∵∆AD'B'\)是正三角形, \(:<\overrightarrow{D^{\prime} A}, \overrightarrow{D^{\prime} B^{\prime}}>=60^{\circ}\),
\(\therefore \overrightarrow{D^{\prime} A} \cdot \overrightarrow{D^{\prime} B^{\prime}}=\left|\overrightarrow{D^{\prime} A}\right| \cdot\left|\overrightarrow{D^{\prime} B^{\prime}}\right| \cdot \cos <\overrightarrow{D^{\prime} A}, \overrightarrow{D^{\prime} B^{\prime}}>=\sqrt{2} \cdot \sqrt{2} \cdot \dfrac{\sqrt{2}}{2}=\sqrt{2}\);
\(\overrightarrow{A D^{\prime}} \cdot \overrightarrow{B C}=\overrightarrow{A D^{\prime}} \cdot \overrightarrow{A D}=\left|\overrightarrow{A D^{\prime}}\right| \cdot|\overrightarrow{A D}| \cdot \cos <\overrightarrow{A D^{\prime}}, \overrightarrow{A D}>=\sqrt{2} \cdot 1 \cdot \cos 45^{\circ}=1\).
空间向量数量积的性质
(1) \(\vec{a} \perp \vec{b} \Rightarrow \vec{a} \cdot \vec{b}=0\). (2) \(|\vec{a}|^{2}=\vec{a}^{2}\).
空间向量数量积运算律
1 \((\lambda \vec{a}) \cdot \vec{b}=\lambda(\vec{a} \cdot \vec{b})=\vec{a}(\lambda \cdot \vec{b})\)
2 \(\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a}\) (交换律)
3 \(\vec{a} \cdot(\vec{b}+\vec{c})=\vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c}\) (分配律)
4 不满足乘法结合律: \((\vec{a} \cdot \vec{b}) \cdot \vec{c} \neq \vec{a} \cdot(\vec{b} \cdot \vec{c})\)
【例】 如图,正方体\(ABCD-A'B'C'D'\)的棱长为\(1\),设 \(\overrightarrow{A B}=\vec{a}\), \(\overrightarrow{A D}=\vec{b}\), \(\overrightarrow{A A^{\prime}}=\vec{c}\),求:
(1) \(\vec{a} \cdot(\vec{b}+\vec{c})\); (2) \((\vec{a}+\vec{b})^{2}\)
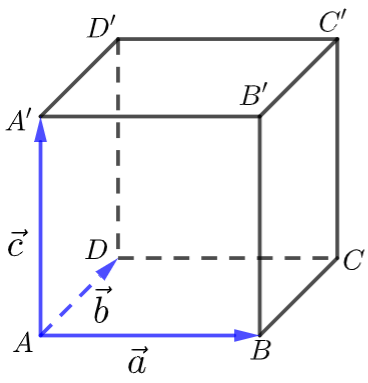
解析 (1) \(\vec{a} \cdot(\vec{b}+\vec{c})=\vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c}=0+0=0\);
(2)方法1 \((\vec{a}+\vec{b})^{2}=\vec{a}^{2}+2 \vec{a} \cdot \vec{b}+\vec{b}^{2}=1+0+1=2\);
方法2 \((\vec{a}+\vec{b})^{2}=\overrightarrow{A C}^{2}=|\overrightarrow{A C}|^{2}=\sqrt{2}^{2}=2\).
基本方法
【题型1】数量积的运算
【典题1】 已知四面体\(ABCD\)的所有棱长都是\(2\),\(E,F,G\)分别是棱\(AB\),\(AD\),\(DC\)的中点,则( )
A. \(\overrightarrow{A B} \cdot \overrightarrow{A C}=2\) \(\qquad \qquad\) B. \(\overrightarrow{E F} \cdot \overrightarrow{F G}=1\) \(\qquad \qquad\) C. \(\overrightarrow{A B} \cdot \overrightarrow{E G}=0\) \(\qquad \qquad\) D. \(\overrightarrow{G E} \cdot \overrightarrow{G F}=1\)
解析 由题意,空间四边形\(ABCD\)的每条边及\(AC\),\(BD\)的长都为\(2\),四面体时正四面体,

所以每个面都是等边三角形,点\(E,F,G\)分别是\(AB,AD,DC\)的中点,
所以 \(\overrightarrow{A B} \cdot \overrightarrow{A C}=|\overrightarrow{A B} \| \overrightarrow{A C}| \cos 60^{\circ}=2\),故\(A\)正确;
\(\overrightarrow{E F} \cdot \overrightarrow{F G}=\dfrac{1}{2} \overrightarrow{B D} \cdot \dfrac{1}{2} \overrightarrow{A C}=\dfrac{1}{4} \overrightarrow{B D} \cdot(\overrightarrow{B C}-\overrightarrow{B A})=\dfrac{1}{4} \overrightarrow{B D} \cdot \overrightarrow{B C}-\dfrac{1}{4} \overrightarrow{B D} \cdot \overrightarrow{B A}=0\),故\(B\)错误;
\(\overrightarrow{A B} \cdot \overrightarrow{E G}=\overrightarrow{A B} \cdot(\overrightarrow{F G}-\overrightarrow{F E})=\overrightarrow{A B} \cdot \dfrac{1}{2} \overrightarrow{A C}-\overrightarrow{A B} \cdot \dfrac{1}{2} \overrightarrow{D B}=1-\dfrac{1}{2} \overrightarrow{B A} \cdot \overrightarrow{B D}=1-1=0\),故\(C\)正确;
\(\overrightarrow{G E} \cdot \overrightarrow{G F}=(\overrightarrow{G C}+\overrightarrow{C B}+\overrightarrow{B E}) \cdot \overrightarrow{G F}=\overrightarrow{G C} \cdot \overrightarrow{G F}+\overrightarrow{C B} \cdot \overrightarrow{G F}+\overrightarrow{B E} \cdot \overrightarrow{G F}\)\(=\dfrac{1}{2} \overrightarrow{D C} \cdot \dfrac{1}{2} \overrightarrow{C A}+\dfrac{1}{2} \overrightarrow{C B} \cdot \overrightarrow{C A}+\dfrac{1}{2} \overrightarrow{B A} \cdot \dfrac{1}{2} \overrightarrow{C A}=-\dfrac{1}{2}+1+\dfrac{1}{2}=1\),
故\(D\)正确.
故选:\(ACD\).
【典题2】已知\(MN\)是正方体内切球的一条直径,点\(P\)在正方体表面上运动,正方体的棱长是\(2\),则 \(\overrightarrow{P M} \cdot \overrightarrow{P N}\)的取值范围为\(\underline{\quad \quad}\).
解析

设正方体内切球球心为\(S\),\(MN\)是该内切球的任意一条直径,则内切球的半径为\(1\),
所以 \(\overrightarrow{P M} \cdot \overrightarrow{P N}=(\overrightarrow{P S}+\overrightarrow{S M}) \cdot(\overrightarrow{P S}+\overrightarrow{S N})=(\overrightarrow{P S}+\overrightarrow{S M}) \cdot(\overrightarrow{P S}-\overrightarrow{S M})=\overrightarrow{P S^{2}}-1 \in[0,2]\).
所以 \(\overrightarrow{P M} \cdot \overrightarrow{P N}\)的取值范围是\([0,2]\).
巩固练习
1 已知空间四面体\(D-ABC\)的每条棱长都等于\(1\),点\(E,F\)分别是\(AB\),\(AD\)的中点,则 \(\overrightarrow{E F} \cdot \overrightarrow{D C}\)等于( )
A. \(\dfrac{1}{4}\) \(\qquad \qquad\) B. \(-\dfrac{1}{4}\)\(\qquad \qquad\) C. \(\dfrac{\sqrt{3}}{4}\) \(\qquad \qquad\) D. \(-\dfrac{\sqrt{3}}{4}\)
2 已知四面体\(ABCD\),所有棱长均为\(2\),点\(E,F\)分别为棱\(AB\),\(CD\)的中点,则 \(\overrightarrow{A F} \cdot \overrightarrow{C E}=\)( )

A.\(1\) \(\qquad \qquad\) B.\(2\) \(\qquad \qquad\) C.\(-1\) \(\qquad \qquad\) D.\(-2\)
3 已知球\(O\)内切于正四面体\(A-BCD\),且正四面体的棱长为 \(2 \sqrt{6}\),线段\(MN\)是球\(O\)的一条动直径(\(M,N\)是直径的两端点),点\(P\)是正四面体\(A-BCD\)的表面上的一个动点,则 \(\overrightarrow{P M} \cdot \overrightarrow{P N}\)的最大值是\(\underline{\quad \quad}\).
参考答案
-
答案 \(B\)
解析 如图:\(∵\)点\(E,F\)分别是\(AB,AD\)的中点, \(\therefore \overrightarrow{E F}=\dfrac{1}{2} \overrightarrow{B D}\),
\(∵\)空间四面体\(D-ABC\)的每条棱长都等于\(1\),\(∴\)每个面都是等边三角形,

\(\therefore \overrightarrow{E F} \cdot \overrightarrow{D C}=\dfrac{1}{2} \overrightarrow{B D} \cdot \overrightarrow{D C}=-\dfrac{1}{2} \overrightarrow{D B} \cdot \overrightarrow{D C}=-\dfrac{1}{2} \cdot|\overrightarrow{D B}| \cdot|\overrightarrow{D C}| \cdot \cos \dfrac{\pi}{3}\)\(=-\dfrac{1}{2} \times 1 \times 1 \times \dfrac{1}{2}=-\dfrac{1}{4}\),
故选:\(B\). -
答案 \(D\)
解析 \(∵\)四面体\(ABCD\),所有棱长均为\(2\),\(∴\)四面体\(ABCD\)为正四面体,
\(∵E,F\)分别为棱\(AB\),\(CD\)的中点,
\(\therefore \overrightarrow{A F} \cdot \overrightarrow{C E}=\dfrac{1}{2}(\overrightarrow{A C}+\overrightarrow{A D}) \cdot(\overrightarrow{A E}-\overrightarrow{A C})\)\(=\dfrac{1}{2} \overrightarrow{A C} \cdot \overrightarrow{A E}-\dfrac{1}{2} \overrightarrow{A C}^{2}+\dfrac{1}{2} \overrightarrow{A D} \cdot \overrightarrow{A E}-\dfrac{1}{2} \overrightarrow{A D} \cdot \overrightarrow{A C}\)
\(=\dfrac{1}{2} \times 2 \times 1 \times \dfrac{1}{2}-\dfrac{1}{2} \times 4+\dfrac{1}{2} \times 2 \times 1 \times \dfrac{1}{2}-\dfrac{1}{2} \times 2 \times 2 \times \dfrac{1}{2}\)
\(=-2\).
故选:\(D\). -
答案 \(8\)
解析 由正四面体棱长为 \(2 \sqrt{6}\),则其内切圆的半径为\(1\),
由题意,\(M,N\)是直径的两端点,可得 \(\overrightarrow{O M}+\overrightarrow{O N}=\overrightarrow{0}, \overrightarrow{O M} \cdot \overrightarrow{O N}=-1\),
则 \(\overrightarrow{P M} \cdot \overrightarrow{P N}=(\overrightarrow{P O}+\overrightarrow{O M}) \cdot(\overrightarrow{P O}+\overrightarrow{O N})=\overrightarrow{P O^{2}}+\overrightarrow{P O} \cdot(\overrightarrow{O M}+\overrightarrow{O N})+\overrightarrow{O M} \cdot \overrightarrow{O N}\)
\(=\overrightarrow{P O}^{2}+0-1=\overrightarrow{P O}^{2}-1\),
当点\(P\)在正四面体顶点时, \(\overrightarrow{P O}^{2}\)最大,且最大值为\(9\),
则 \(\overrightarrow{P O}^{2}-1\)的最大值为\(8\).
【题型2】数量积的应用
【典题1】 如图,在平行六面体\(ABCD-A_1 B_1 C_1 D_1\)中,\(AB=5\),\(AD=3\),\(AA_1=4\),\(∠DAB=90^∘\),\(∠BAA_1=∠DAA_1=60^∘\), \(E\)是 \(CC_1\)的中点,求\(AE\)的长.

解析 \(\because|\overrightarrow{A E}|^{2}=\left(\overrightarrow{A B}+\overrightarrow{A D}+\dfrac{1}{2} \overrightarrow{A A_{1}}\right)^{2}\)
\(=\overrightarrow{A B}^{2}+\overrightarrow{A D}^{2}+\dfrac{1}{4}{\overrightarrow{A A_{1}}}^{2}+2 \overrightarrow{A B} \cdot \overrightarrow{A D}+\overrightarrow{A B} \cdot \overrightarrow{A A_{1}}+\overrightarrow{A D} \cdot \overrightarrow{A A_{1}}\)
\(=25+9+4+0+(20+12) \cdot \cos 60^{\circ}=54\)
\(\therefore|\overrightarrow{A E}|=3 \sqrt{6}\),
即\(AE\)的长为 \(3 \sqrt{6}\).
【典题2】证明线面垂直的判断定理
如图,\(m,n\)是平面\(α\)内的两条相交直线,如果\(l⊥m\),\(l⊥n\),求证\(l⊥α\).

证明 在平面\(α\)内作任意一条直线\(g\),分别在直线\(l,m,n,g\)上取非零向量 \(\vec{l}, \vec{m}, \vec{n}, \vec{g}\),
因为直线\(m\)与\(n\)相交,所以向量\(\vec{m},\) \(\vec{n}\)不平行,由向量共面的充要条件可知,存在唯一的有序实数对\((x,y)\),使\(\vec{g}=x\vec{m}+y\vec{n}\),两边分别与向量\(\vec{l}\)作数量积运算,得 \(\vec{l} \cdot \vec{g}=x \vec{l} \cdot \vec{m}+y \vec{l} \cdot \vec{n}\),
因为 \(\vec{l} \cdot \vec{m}=0\), \(\vec{l} \cdot \vec{n}=0\),所以 \(\vec{l} \cdot \vec{g}=0\),所以\(l⊥g\),
由于\(g\)的任意性,则直线\(l\)垂直于平面\(α\)内的任意一条直线,所以\(l⊥α\).
巩固练习
1 如图,在正四面体\(O-ABC\)中,边长为\(1\),\(D\)为\(BC\)的中点,\(E\)为\(AD\)的中点,则 \(|\overrightarrow{O E}|=\)\(\underline{\quad \quad}\).

2 已知:在空间四边形\(OABC\)中(如图),\(OA⊥BC\),\(OB⊥AC\),求证:\(OC⊥AB\).

参考答案
-
答案 \(\dfrac{\sqrt{11}}{4}\)
解析 \(∵D\)为\(BC\)的中点, \(\therefore \overrightarrow{O D}=\dfrac{1}{2} \overrightarrow{O B}+\dfrac{1}{2} \overrightarrow{O C}\),
\(∵E\)为\(AD\)的中点, \(\therefore \overrightarrow{O E}=\dfrac{1}{2}(\overrightarrow{O A}+\overrightarrow{O D})=\dfrac{1}{2} \overrightarrow{O A}+\dfrac{1}{4} \overrightarrow{O B}+\dfrac{1}{4} \overrightarrow{O C}\),
\(∵\)若四面体\(O-ABC\)为正四面体,且边长为\(1\),
\(\therefore|\overrightarrow{O E}|^{2}=\left(\dfrac{1}{2} \overrightarrow{O A}+\dfrac{1}{4} \overrightarrow{O B}+\dfrac{1}{4} \overrightarrow{O C}\right)^{2}\)
\(=\dfrac{1}{4} \overrightarrow{O A}^{2}+\dfrac{1}{16} \overrightarrow{O B}^{2}+\dfrac{1}{16} \overrightarrow{O C}^{2}+\dfrac{1}{4} \overrightarrow{O A} \cdot \overrightarrow{O B}+\dfrac{1}{4} \overrightarrow{O A} \cdot \overrightarrow{O C}+\dfrac{1}{8} \overrightarrow{O C} \cdot \overrightarrow{O B}\)
\(=\dfrac{1}{4}+\dfrac{1}{16}+\dfrac{1}{16}+\dfrac{1}{4} \times 1 \times 1 \times \dfrac{1}{2}+\dfrac{1}{4} \times 1 \times 1 \times \dfrac{1}{2}+\dfrac{1}{8} \times 1 \times 1 \times \dfrac{1}{2}=\dfrac{11}{16}\),
\(\therefore|\overrightarrow{O E}|=\dfrac{\sqrt{11}}{4}\). -
证明 由已知,得 \(\overrightarrow{O A} \perp \overrightarrow{B C}, \overrightarrow{O B} \perp \overrightarrow{A C}\), \(\therefore \overrightarrow{O A} \cdot \overrightarrow{B C}=0, \overrightarrow{O B} \cdot \overrightarrow{A C}=0\),
\(\overrightarrow{O A} \cdot(\overrightarrow{O C}-\overrightarrow{O B})=0\), \(\overrightarrow{O B} \cdot(\overrightarrow{O C}-\overrightarrow{O A})=0\),
\(\therefore \overrightarrow{O A} \cdot \overrightarrow{O C}=\overrightarrow{O A} \cdot \overrightarrow{O B}\), \(\overrightarrow{O B} \cdot \overrightarrow{O C}=O B \cdot \overrightarrow{O A}\),
\(\therefore \overrightarrow{O A} \cdot \overrightarrow{O C}-\overrightarrow{O B} \cdot \overrightarrow{O C}=0\), \(\quad(\overrightarrow{O A}-\overrightarrow{O B}) \cdot \overrightarrow{O C}=0\),\(\overrightarrow{B A} \cdot \overrightarrow{O C}=0\)
\(\therefore \overrightarrow{O C} \perp \overrightarrow{A B}\),\(∴OC⊥AB\).
分层练习
【A组---基础题】
1 在棱长为\(1\)的正方体\(ABCD-A_1 B_1 C_1 D_1\)中,设 \(\overrightarrow{A B}=\vec{a}, \overrightarrow{A D}=\vec{b}, \overrightarrow{A A_{1}}=\vec{c}\),则 \(\vec{a} \cdot(\vec{b}+\vec{c})\)的值为 ( )
A.\(1\) \(\qquad \qquad\) B.\(0\) \(\qquad \qquad\) C.\(-1\) \(\qquad \qquad\) D.\(-2\)
2 在的棱长为\(1\)的正四面体\(ABCD\)中,\(E\)是\(BC\)的中点,则 \(\overrightarrow{A E} \cdot \overrightarrow{C D}=\)( )
A.\(0\) \(\qquad \qquad\) B. \(\dfrac{1}{2}\) \(\qquad \qquad\) C. \(-\dfrac{1}{2}\) \(\qquad \qquad\) D. \(-\dfrac{1}{4}\)
3 在空间四边形\(ABCD\)中,\(AB=BC=CD=DA=1\), \(\overrightarrow{A B} \cdot \overrightarrow{C D}+\overrightarrow{A C} \cdot \overrightarrow{D B}+\overrightarrow{A D} \cdot \overrightarrow{B C}=\) ( )
A.\(-1\) \(\qquad \qquad\) B.\(0\) \(\qquad \qquad\) C.\(1\) \(\qquad \qquad\) D.不确定
4 设正四面体\(ABCD\)的棱长为\(a\),\(E,F\)分别是\(BC\),\(AD\)的中点,则 \(\overrightarrow{A E} \cdot \overrightarrow{A F}\)的值为( )
A. \(\dfrac{1}{4} a^{2}\) \(\qquad \qquad\) B. \(\dfrac{1}{2} a^{2}\) \(\qquad \qquad\) C. \(a^{2}\) \(\qquad \qquad\) D. \(\dfrac{\sqrt{3}}{4} a^{2}\)
5 平面上有四个互异点\(A、B、C、D\),已知 \((\overrightarrow{D B}+\overrightarrow{D C}+2 \overrightarrow{A D}) \cdot(\overrightarrow{A B}-\overrightarrow{A C})=0\),则\(△ABC\)的形状是( )
A.直角三角形 \(\qquad \qquad\) B.等腰直角三角形 \(\qquad \qquad\) C.等腰三角形 \(\qquad \qquad\) D.无法确定
6 在平行六面体(底面是平行四边形的四棱柱)\(ABCD-A_1 B_1 C_1 D_1\)中,\(AB=AD=AA_1=1\),\(∠BAD=∠BAA_1=∠DAA_1=60°\),则\(AC_1\)的长为( )

A.\(3\) \(\qquad \qquad\) B. \(\sqrt{3}\) \(\qquad \qquad\) C.\(6\) \(\qquad \qquad\) D. \(\sqrt{6}\)
7 在四棱锥\(S-ABCD\) 中,四边形\(ABCD\)为正方形,\(AB=AD=SA=1\),且\(SA⊥\)底面\(ABCD\),则向量 \(\overrightarrow{C S}\)在平面\(ABCD\)上的投影向量是\(\underline{\quad \quad}\), \(\overrightarrow{C S} \cdot \overrightarrow{A B}=\)\(\underline{\quad \quad}\).
8 已知三棱锥\(A-BCD\)每条棱长都为\(1\),点\(E,G\)分别是\(AB,DC\)的中点,则 \(\overrightarrow{G E} \cdot \overrightarrow{A C}=\)\(\underline{\quad \quad}\).
9 如图,四棱锥\(O-ABCD\)中,\(AC\)垂直平分\(BD\), \(|\overrightarrow{O B}|=2,|\overrightarrow{O D}|=1\),则 \((\overrightarrow{O A}+\overrightarrow{O C}) \cdot(\overrightarrow{O B}-\overrightarrow{O D})\)的值是\(\underline{\quad \quad}\).

10 如图所示,在正方体\(ABCD-A_1 B_1 C_1 D_1\)中,求异面直线\(A_1 B\)与\(AC\)所成的角.

11 在三棱锥\(O-ABC\)中,已知侧棱\(OA,OB,OC\)两两垂直,用空间向量知识证明:底面三角形\(ABC\)是锐角三角形.

12 已知空间四边形\(OABC\)中,\(∠AOB=∠BOC=∠AOC\),且\(OA=OB=OC\).\(M、N\)分别是\(OA\)、\(BC\)的中点,\(G\)是\(MN\)的中点,求证:\(OG⊥BC\).

参考答案
-
答案 \(B\)
解析 由正方体的性质可得, \(\overrightarrow{A B} \perp \overrightarrow{A D}\), \(\overrightarrow{A B} \perp \overrightarrow{A A_{1}}\),故 \(\overrightarrow{A B} \cdot \overrightarrow{A D}=0\), \(\overrightarrow{A B} \cdot \overrightarrow{A A_{1}}=0\),
\(∵\overrightarrow{A B}=\vec{a}, \overrightarrow{A D}=\vec{b}, \overrightarrow{A A_{1}}=\vec{c}\),
\(\therefore \vec{a} \cdot(\vec{b}+\vec{c})=\overrightarrow{A B} \cdot\left(\overrightarrow{A D}+\overrightarrow{A A_{1}}\right)=\overrightarrow{A B} \cdot \overrightarrow{A D}+\overrightarrow{A B} \cdot \overrightarrow{A A_{1}}=0\).故选:\(B\). -
答案 \(D\)
解析 由题意作以下图形:
\(∵\)正四面体\(ABCD\)的棱长为\(1\),取\(BC\),\(BD\)的中点\(E,F\),则 \(\overrightarrow{E F}=\dfrac{1}{2} \overrightarrow{C D}\),
\(∵\)正四面体\(ABCD\)的所有棱长为\(1\), \(\therefore|\overrightarrow{A E}|=\dfrac{\sqrt{3}}{2}=A F|\overrightarrow{E F}|=\dfrac{1}{2}\);
在\(△AEF\)中有余弦定理可知 \(\cos \angle A E F=\dfrac{\sqrt{3}}{6}\), \(\therefore \cos <\overrightarrow{A E}, \overrightarrow{C D}>=-\dfrac{\sqrt{3}}{6}\);
由平面向量的数量积的定义可知
\(\overrightarrow{A E} \cdot \overrightarrow{C D}=|\overrightarrow{A E}| \cdot|\overrightarrow{C D}| \cdot \cos \langle\overrightarrow{A E}, \overrightarrow{C D}\rangle=\dfrac{\sqrt{3}}{2} \times 1 \times\left(-\dfrac{\sqrt{3}}{6}\right)=-\dfrac{1}{4}\);
故选:\(D\).

-
答案 \(B\)
解析 根据题意, \(\overrightarrow{A B} \cdot \overrightarrow{C D}+\overrightarrow{A C} \cdot \overrightarrow{D B}+\overrightarrow{A D} \cdot \overrightarrow{B C}\)
\(=\overrightarrow{A B} \cdot(\overrightarrow{A D}-\overrightarrow{A C})+\overrightarrow{A C} \cdot(\overrightarrow{A B}-\overrightarrow{A D})+\overrightarrow{A D} \cdot(\overrightarrow{A C}-\overrightarrow{A B})\)
\(=\overrightarrow{A B} \cdot \overrightarrow{A D}-\overrightarrow{A B} \cdot \overrightarrow{A C}+\overrightarrow{A C} \cdot \overrightarrow{A B}-\overrightarrow{A C} \cdot \overrightarrow{A D}+\overrightarrow{A D} \cdot \overrightarrow{A C}-\overrightarrow{A D} \cdot \overrightarrow{A B}=0\),
故选:\(B\). -
答案 \(A\)
解析 如图所示, \(\overrightarrow{A E}=\dfrac{1}{2}(\overrightarrow{A B}+\overrightarrow{A C})\), \(\overrightarrow{A F}=\dfrac{1}{2} \overrightarrow{A D}\).
\(\therefore \overrightarrow{A E} \cdot \overrightarrow{A F}=\dfrac{1}{2}(\overrightarrow{A B}+\overrightarrow{A C}) \cdot \dfrac{1}{2} \overrightarrow{A D}=\dfrac{1}{4}(\overrightarrow{A B} \cdot \overrightarrow{A D}+\overrightarrow{A C} \cdot \overrightarrow{A D})\)
\(=\dfrac{1}{4}\left(a^{2} \cos 60^{\circ}+a^{2} \cos 60^{\circ}\right)=\dfrac{1}{4} a^{2}\).
故选:\(A\).

-
答案 \(C\)
解析 \(\because((\overrightarrow{D B}+\overrightarrow{D C}+2 \overrightarrow{A D}) \cdot(\overrightarrow{A B}-\overrightarrow{A C})=0\),
\(\therefore(\overrightarrow{A B}+\overrightarrow{A C}) \cdot(\overrightarrow{A B}-\overrightarrow{A C})=0\) ,可得 \(\overrightarrow{A B^{2}}=\overrightarrow{A C^{2}}\).可得\(AB=AC\).
则\(△ABC\)的形状是等腰三角形.故选:\(C\). -
答案 \(D\)
解析 \(\overrightarrow{A C}_{1}=\overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{A A_{1}}\),
则 \(\overrightarrow{A C_{1}^{2}}=\left(\overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{A A_{1}}\right)^{2}\)
\(=\overrightarrow{A B}^{2}+\overrightarrow{A D}^{2}+\overrightarrow{A A}_{1}^{2}+2 \overrightarrow{A B} \cdot \overrightarrow{A D}+2 \overrightarrow{A B} \cdot \overrightarrow{A A_{1}}+2 \overrightarrow{A D} \cdot \overrightarrow{A A}_{1}\)
\(=1+1+1+3×2×1×1×cos60°=6\).
\(\therefore\left|\overrightarrow{A C}_{1}\right|=\sqrt{6}\).
故选:\(D\). -
答案 \(\overrightarrow{C A}\),\(-1\)
解析 如图,

\(∵SA⊥\)底面\(ABCD\),\(∴\)向量 \(\overrightarrow{C S}\)在平面\(ABCD\)上的投影向量是 \(\overrightarrow{C A}\),
\(∵SA⊥\)底面\(ABCD\), \(\therefore \overrightarrow{S A} \cdot \overrightarrow{A B}=0\),
\(∵\)四边形\(ABCD\)为正方形,\(AB=AD=SA=1\),
\(\therefore \overrightarrow{C S} \cdot \overrightarrow{A B}=(\overrightarrow{A S}-\overrightarrow{A C}) \cdot \overrightarrow{A B}=-\overrightarrow{A C} \cdot \overrightarrow{A B}=-(\overrightarrow{A B}+\overrightarrow{A D}) \cdot \overrightarrow{A B}=-\overrightarrow{A B}^{2}=-1\). -
答案 \(-\dfrac{1}{2}\)
解析 如图, \(\because \overrightarrow{G E}=\overrightarrow{G D}+\overrightarrow{D A}+\overrightarrow{A E}=\dfrac{1}{2} \overrightarrow{C D}-\overrightarrow{A D}+\dfrac{1}{2} \overrightarrow{A B}\)
\(=\dfrac{1}{2} \overrightarrow{A D}-\dfrac{1}{2} \overrightarrow{A C}-\overrightarrow{A D}+\dfrac{1}{2} \overrightarrow{A B}=\dfrac{1}{2} \overrightarrow{A B}-\dfrac{1}{2} \overrightarrow{A C}-\dfrac{1}{2} \overrightarrow{A D}\),
\(\therefore \overrightarrow{G E} \cdot \overrightarrow{A C}=\left(\dfrac{1}{2} \overrightarrow{A B}-\dfrac{1}{2} \overrightarrow{A C}-\dfrac{1}{2} \overrightarrow{A D}\right) \cdot \overrightarrow{A C}=\dfrac{1}{2} \overrightarrow{A B} \cdot \overrightarrow{A C}-\dfrac{1}{2} \overrightarrow{A C}^{2}-\dfrac{1}{2} \overrightarrow{A D} \cdot \overrightarrow{A C}\)\(=-\dfrac{1}{2} \overrightarrow{A C}^{2}=-\dfrac{1}{2}\).

-
答案 \(3\)
解析 如图所示,四棱锥\(O-ABCD\)中,设 \(AC,BD\)交于点\(E\),
由题意\(AC⊥BD\),\(DE=BE\),
\(\therefore \overrightarrow{O B}+\overrightarrow{O D}=2 \overrightarrow{O E}\), \(\overrightarrow{E A} \cdot \overrightarrow{D B}=\overrightarrow{E C} \cdot \overrightarrow{D B}=0\);
又 \(|\overrightarrow{O B}|=2,|\overrightarrow{O D}|=1\),
\(\therefore(\overrightarrow{O A}+\overrightarrow{O C}) \cdot(\overrightarrow{O B}-\overrightarrow{O D})=(\overrightarrow{O E}+\overrightarrow{E A}+\overrightarrow{O E}+\overrightarrow{E C}) \cdot(\overrightarrow{O B}-\overrightarrow{O D})\)
\(=(2 \overrightarrow{O E}+\overrightarrow{E A}+\overrightarrow{E C}) \cdot(\overrightarrow{O B}-\overrightarrow{O D})=2 \overrightarrow{O E} \cdot(\overrightarrow{O B}-\overrightarrow{O D})+(\overrightarrow{E A}+\overrightarrow{E C}) \cdot \overrightarrow{D B}\)
\(=(\overrightarrow{O B}+\overrightarrow{O D}) \cdot(\overrightarrow{O B}-\overrightarrow{O D})=\overrightarrow{O B}^{2}-\overrightarrow{O D}^{2}=2^{2}-1^{2}=3\).
故答案为:\(3\).

-
答案 \(60°\)
解析 不妨设正方体的棱长为\(1\),设 \(\overrightarrow{A B}=\vec{a}, \overrightarrow{A D}=\vec{b}, A \vec{A}_{1}=\vec{c}\),
则 \(|\vec{a}|=|\vec{b}|=|c|=1\),\(\vec{a} \cdot \vec{b}=\vec{b} \cdot c=c \cdot \vec{a}=0\)
\(\overrightarrow{A_{1} B}=\vec{a}-\vec{c}\), \(\overrightarrow{A C}=\vec{a}+\vec{b}\),
\(\therefore \overrightarrow{A_{1} B} \cdot \overrightarrow{A C}=(\vec{a}-\vec{c}) \cdot(\vec{a}+\vec{b})=|\vec{a}|^{2}+\vec{a} \cdot \vec{b}-\vec{a} \cdot \vec{c}-\vec{b} \cdot \vec{c}=1\),
而 \(\left|\overrightarrow{A_{1} B}\right|=|\overrightarrow{A C}|=\sqrt{2}\), \(\therefore \cos \left\langle\overrightarrow{A_{1} B}, \overrightarrow{A C}\right\rangle=\dfrac{1}{\sqrt{2} \times \sqrt{2}}=\dfrac{1}{2}\),
\(\therefore\left\langle\overrightarrow{A_{1} B}, \overrightarrow{A C}\right\rangle=60^{\circ}\),
所以异面直线\(A_1B\)与\(AC\)所成的角为\(60°\). -
证明 \(∵OA,OB,OC\)两两互相垂直.
\(\therefore \overrightarrow{A B} \cdot \overrightarrow{A C}=(\overrightarrow{O B}-\overrightarrow{O A}) \cdot(\overrightarrow{O C}-\overrightarrow{O A})=\overrightarrow{O A^{2}}=|\overrightarrow{O A}|^{2}>0\),
\(\therefore<\overrightarrow{A B}, \overrightarrow{A C}>\)为锐角,即\(∠BAC\)为锐角,
同理\(∠ABC,∠BCA\)均为锐角,
\(∴△ABC\)为锐角三角形. -
证明 如图所示,连接\(ON\),设\(∠AOB=∠BOC=∠AOC=θ\),
又设 \(\overrightarrow{O A}=\vec{a}, \overrightarrow{O B}=\vec{b}, \overrightarrow{O C}=\vec{c}\),则 \(|\vec{a}|=|\vec{b}|=|\vec{c}|\),
又 \(\overrightarrow{O G}=\dfrac{1}{2}(\overrightarrow{O M}+\overrightarrow{O N})=\dfrac{1}{2}\left[\dfrac{1}{2} \overrightarrow{O A}+\dfrac{1}{2}(\overrightarrow{O B}+\overrightarrow{O C})\right]=\dfrac{1}{4}(\vec{a}+\vec{b}+\vec{c})\), \(\overrightarrow{B C}=\vec{c}-\vec{b}\).
\(\therefore \overrightarrow{O G} \cdot \overrightarrow{B C}=\dfrac{1}{4}(\vec{a}+\vec{b}+\vec{c})(c-\vec{b})\)\(=\dfrac{1}{4}\left(|\vec{a}|^{2} \cos \theta-|\vec{a}|^{2} \cos \theta-|\vec{a}|^{2}+|\vec{a}|^{2}\right)=0\),
\(∴OG⊥BC\).
【B组---提高题】
1.已知四面体\(P-ABC\),\(∠PAB=∠BAC=∠PAC=60^∘\), \(|\overrightarrow{A B}|=1\), \(|\overrightarrow{A C}|=2\), \(|\overrightarrow{A P}|=3\),则 \(|\overrightarrow{A B}+\overrightarrow{A P}+\overrightarrow{A C}|=\)\(\underline{\quad \quad}\).
2.如图,在三棱锥\(A-BCD\)中,\(AB=AC=BD=CD=3\),\(AD=BC=2\),\(M,N\)分别是\(AD\)、\(BC\)的中点,则 \(\overrightarrow{A N} \cdot \overrightarrow{C M}=\)\(\underline{\quad \quad}\).

3.已知球\(O\)是棱长为\(2\)的正八面体(八个面都是全等的等边三角形)的内切球,\(MN\)为球\(O\)的一条直径,点\(P\)为正八面体表面上的一个动点,则 \(\overrightarrow{P M} \cdot \overrightarrow{P N}\)的取值范围是\(\underline{\quad \quad}\).
4.如图,三棱锥\(O-ABC\)各棱的棱长都是\(1\),点\(D\)是棱\(AB\)的中点,点\(E\)在棱\(OC\)上,且 \(\overrightarrow{O E}=\lambda \overrightarrow{O C}\),记 \(\overrightarrow{O A}=\vec{a}, \overrightarrow{O B}=\vec{b}, \overrightarrow{O C}=\vec{c}\).
(1)用向量 \(\vec{a}, \vec{b}, \vec{c}\)表示向量 \(\overrightarrow{D E}\);(2)求\(DE\)的最小值.

5.如图,\(60^{\circ}\)的二面角的棱上有\(A、B\)两点,直线\(AC、BD\)分别在这个二面角的两个半平面内,且都垂直于\(AB\).已知\(AB=2\),\(AC=3\),\(BD=4\),求\(CD\)的长.

6.如图,在平行四边形\(ABCD\)中,\(AB=AC=1\),\(∠ACD=90^{\circ}\),将它沿对角线\(AC\)折起,使\(AB\)与\(CD\)成\(60^{\circ}\)角,求\(B、D\)间的距离.

参考答案
-
答案 \(5\)
解析 \(|\overrightarrow{A B}+\overrightarrow{A P}+\overrightarrow{A C}|^{2}=\overrightarrow{A B}^{2}+\overrightarrow{A P}^{2}+\overrightarrow{A C}^{2}+2 \overrightarrow{A B} \cdot \overrightarrow{A P}+2 \overrightarrow{A C} \cdot \overrightarrow{A P}+\overrightarrow{A B} \cdot \overrightarrow{A C}\)
\(=1+4+9+2×1×2×\cos60^∘+2×2×3×\cos60^∘+2×1×3×\cos60^∘=25\);
则 \(|\overrightarrow{A B}+\overrightarrow{A P}+\overrightarrow{A C}|=5\). -
答案 \(-7\)
解析 在三棱锥\(A-BCD\)中,连结\(ND\),取\(ND\)的中点为\(E\),连结\(ME\),则\(ME//AN\),
异面直线\(AN,CM\)所成的角就是\(∠EMC\).
\(∵AB=AC=BD=CD=3\),\(AD=BC=2\),点\(M,N\)分别是\(AD、BC\)的中点,
\(\therefore A N=2 \sqrt{2}\), \(M E=E N=\sqrt{2}\), \(M C=2 \sqrt{2}\),
又\(∵EN⊥NC\), \(\therefore E C=\sqrt{N C^{2}+N E^{2}}=\sqrt{3}\).
\(\cos \angle E M C=\dfrac{M C^{2}+M E^{2}-E C^{2}}{2 M C \cdot M E}=\dfrac{2+8-3}{2 \times \sqrt{2} \times 2 \sqrt{2}}=\dfrac{7}{8}\).
由图可知, \(\overrightarrow{A N}\)与 \(\overrightarrow{C M}\)所成角为钝角,则 \(\cos \langle\overrightarrow{A N}, \overrightarrow{C M}\rangle=-\dfrac{7}{8}\).
\(\therefore \overrightarrow{A N} \cdot \overrightarrow{C M}=|\overrightarrow{A N}| \cdot|\overrightarrow{C M}| \cos <\overrightarrow{A N}, \overrightarrow{C M}>=2 \sqrt{2} \times 2 \sqrt{2} \times\left(-\dfrac{7}{8}\right)=-7\).

-
答案 \(\left[\dfrac{1}{3}, \dfrac{4}{3}\right]\)
解析 设球\(O\)的半径为\(R\),则 \(\dfrac{1}{2} \times \sqrt{2} \times 1=\dfrac{1}{2} \times \sqrt{3} \times R\),解得 \(R=\dfrac{\sqrt{6}}{3}\). \(|\overrightarrow{O P}| \in[1, \sqrt{2}]\).
\(\overrightarrow{P M} \cdot \overrightarrow{P N}=(\overrightarrow{O M}-\overrightarrow{O P}) \cdot(\overrightarrow{O N}-\overrightarrow{O P})=\overrightarrow{O P^{2}}-\vec{R}^{2}=\overrightarrow{O P}^{2}-\dfrac{2}{3} \in\left[\dfrac{1}{3}, \dfrac{4}{3}\right]\).
故答案为: \(\left[\dfrac{1}{3}, \dfrac{4}{3}\right]\).

-
答案 (1) \(\overrightarrow{D E}=\lambda \vec{c}-\dfrac{1}{2} \vec{a}-\dfrac{1}{2} \vec{b}\) (2) \(\dfrac{\sqrt{2}}{2}\)
解析 (1)根据题意,连接\(OD,CD\),点\(D\)是棱\(AB\)的中点,点\(E\)在棱\(OC\)上,
且 \(\overrightarrow{O E}=\lambda \overrightarrow{O C}\),记 \(\overrightarrow{O A}=\vec{a}, \overrightarrow{O B}=\vec{b}, \overrightarrow{O C}=\vec{c}\)..
\(\therefore \overrightarrow{D E}=\overrightarrow{O E}-\overrightarrow{O D}=\lambda \overrightarrow{O C}-\dfrac{1}{2}(\overrightarrow{O A}+\overrightarrow{O B})=\lambda \vec{c}-\dfrac{1}{2} \vec{a}-\dfrac{1}{2} \vec{b}\),
(2)根据题意,点\(D\)是棱\(AB\)的中点,则 \(|O D|=\dfrac{\sqrt{3}}{2}\),且 \(\cos \angle D O E=\dfrac{\sqrt{3}}{3} \text {, }\),
\(|\overrightarrow{D E}|^{2}=|\overrightarrow{O E}-\overrightarrow{O D}|^{2}=\overrightarrow{O E}^{2}-2 \overrightarrow{O E} \cdot \overrightarrow{O D}+\overrightarrow{O D}{ }^{2}\)
\(=(\lambda \vec{c})^{2}-2 \times \lambda \times 1 \times \dfrac{\sqrt{3}}{2} \times \cos \angle D O E+\dfrac{3}{4}=\lambda^{2}-\lambda+\dfrac{3}{4}=\left(\lambda-\dfrac{1}{2}\right)^{2}+\dfrac{1}{2},\),
则当 \(\lambda=\dfrac{1}{2}\)时, \(|\overrightarrow{D E}|^{2}\)取得最小值 \(\dfrac{1}{2}\),则 \(| \overrightarrow{D E}|\)的最小值为 \(\dfrac{\sqrt{2}}{2}\).

-
答案 \(\sqrt{17}\)
解析 方法一
如图过点\(A\)作\(AE//BD\),过\(D\)作\(DE//AB\),则易得\(∠CAE=60^°\),\(AE=4\),\(ED=2\),

在\(∆CAE\)中, \(C E^{2}=A C^{2}+A E^{2}-2 A C \cdot A E \cdot \cos \angle C A E=9+16-12=13\)
在\(Rt∆CED\)中, \(C D^{2}=C E^{2}+E D^{2}=13+4=17 \Rightarrow C D=\sqrt{17}\).
方法二 如图, \(\overrightarrow{C D}=\overrightarrow{C A}+\overrightarrow{A B}+\overrightarrow{B D}\),
\(\overrightarrow{C D}^{2}=(\overrightarrow{C A}+\overrightarrow{A B}+\overrightarrow{B D})^{2}=\overrightarrow{C A}^{2}+\overrightarrow{A B}^{2}+\overrightarrow{B D}^{2}+2(\overrightarrow{C A} \cdot \overrightarrow{A B}+\overrightarrow{A B} \cdot \overrightarrow{B D}+\overrightarrow{B D} \cdot \overrightarrow{C A})\)
\(=\overrightarrow{C A}^{2}+\overrightarrow{A B}^{2}+\overrightarrow{B D}^{2}+2 \overrightarrow{B D} \cdot \overrightarrow{C A}=9+4+16+2 \times 4 \times 3 \times \cos 120^{\circ}=17\)
\(∴CD\)的长为 \(\sqrt{17}\). -
答案 \(2\)或 \(\sqrt{2}\)
解析 由题可知 \(\overrightarrow{B D}=\overrightarrow{B A}+\overrightarrow{A C}+\overrightarrow{C D}\),
\(∵∠ACD=90^∘\), \(\therefore \overrightarrow{A C} \cdot \overrightarrow{C D}=0\),同理 \(\overrightarrow{A C} \cdot \overrightarrow{B A}=0 \text {, }\),
\(∵AB\)与\(CD\)成\(60^∘\)角, \(\therefore \angle \overrightarrow{B A}, \overrightarrow{C D}>=60^{\circ}\)或 \(120^{\circ}\),
又 \(\overrightarrow{B D}=\overrightarrow{B A}+\overrightarrow{A C}+\overrightarrow{C D}\),
\(\therefore|\overrightarrow{B D}|^{2}=|\overrightarrow{B A}|^{2}+|\overrightarrow{A C}|^{2}+|\overrightarrow{C D}|^{2}+2 \overrightarrow{B A} \cdot \overrightarrow{A C}+2 \overrightarrow{B A} \cdot \overrightarrow{C D}+2 \overrightarrow{A C} \cdot \overrightarrow{C D}\)
\(=3+2 \times 1 \times 1 \times \cos <\overrightarrow{B A}, \overrightarrow{C D}>= \begin{cases}4 & \left(<\overrightarrow{B A}, C D>=60^{\circ}\right) \\ 2 & \left(<\overrightarrow{B A}, C D>=120^{\circ}\right)\end{cases}\)
\(∴|BD|=2\)或 \(\sqrt{2}\).
即\(B、D\)之间的距离为\(2\)或 \(\sqrt{2}\).
【C组---拓展题】
1 点\(P\)是棱长为 \(2 \sqrt{6}\)的正四面体表面上的动点,\(MN\)是该四面体内切球的一条直径,则 \(\overrightarrow{P M} \cdot \overrightarrow{P N}\)的最大值是\(\underline{\quad \quad}\).
2 如图,在三棱锥\(D-ABC\)中,已知\(AB=2\), \(\overrightarrow{A C} \cdot \overrightarrow{B D}=-3\),设\(AD=a\),\(BC=b\),\(CD=c\),则 \(\dfrac{c^{2}}{a b+1}\)的最小值为\(\underline{\quad \quad}\).

参考答案
-
答案 \(8\)
解析 如图所示:

设正四面体\(ABCD\)的棱长为 \(2 \sqrt{6}\),
设其内切球球心为点\(O\),连接\(AO\)并延长交底面\(BCD\)于点\(E\),
则 为正三角形\(BCD\)的中点,且\(AE⊥\)平面\(BCD\),
连接BE并延长交\(CD\)于点\(F\),则\(F\)为\(CD\)的中点,且\(BF⊥CD\),
\(\therefore B F=\sqrt{B C^{2}-C F^{2}}=3 \sqrt{2}\), \(\therefore B E=\dfrac{2}{3} B F=2 \sqrt{2}\),
\(∵AE⊥\)平面\(BCD\),\(BE⊂\)平面\(BCD\),
\(∴AE⊥BE\), \(\therefore A E=\sqrt{A B^{2}-B E^{2}}=4\),
\(\therefore S_{\triangle B C D}=\dfrac{1}{2} \cdot C D \cdot B F=6 \sqrt{3}\),
\(∴\)正四面体\(ABCD\)的体积 \(V=\dfrac{1}{3} S_{\triangle B C D} \cdot A E=8 \sqrt{3}\),
设球\(O\)的半径为\(R\),
则 \(V=V_{O-B C D}+V_{O-A C D}+V_{O-A B D}+V_{O-A B C}=4 V_{O-B C D}=4 \times \dfrac{1}{3} S_{\triangle B C D} \cdot R\),
\(\therefore R=\dfrac{3 V}{4 S_{\triangle B C D}}=1\),\(∴AO=AE-OE=3\),
\(\because \overrightarrow{P M}=\overrightarrow{P O}+\overrightarrow{O M}\), \(\overrightarrow{P N}=\overrightarrow{P O}+\overrightarrow{O N}=\overrightarrow{P O}-\overrightarrow{O M}\),
\(\therefore \overrightarrow{P M} \cdot \overrightarrow{P N}=(\overrightarrow{P O}+\overrightarrow{O M})(\overrightarrow{P O}-\overrightarrow{O M})=\overrightarrow{P O}^{2}-1\),
当 \(\overrightarrow{P O}^{2}\)最大,即点\(P\)位于正四面体\(ABCD\)的顶点时,则 \(\overrightarrow{P M} \cdot \overrightarrow{P N}\)取最大值,
此时, \(\overrightarrow{P M} \cdot \overrightarrow{P N}=\overrightarrow{P O}^{2}-1 \leqslant A O^{2}-1=9-1=8\).
故答案为:\(8\). -
答案 \(2\)
解析 \(∵\)在三棱锥\(D-ABC\)中,\(AB=2\), \(\overrightarrow{A C} \cdot \overrightarrow{B D}=-3\),
设 \(\overrightarrow{A D}=\vec{a}, \overrightarrow{B C}=\vec{b}, \overrightarrow{C D}=\vec{c}\)
\(\therefore \overrightarrow{A C}=\vec{a}-\vec{c}, \overrightarrow{B D}=\vec{b}+\vec{c}\),
\(\therefore \overrightarrow{A C} \cdot \overrightarrow{B D}=(\vec{a}-\vec{c}) \cdot(\vec{b}+\vec{c})=\vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c}-\vec{b} \cdot \vec{c}-\vec{c}^{2}=-3\),
\(\therefore \vec{c}^{2}=\vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c}-\vec{b} \cdot \vec{c}+3\),
又 \(\overrightarrow{A B}=\vec{a}-\overrightarrow{B D}=\vec{a}-\vec{b}-\vec{c}\), \(\therefore|(\vec{a}-\vec{b})-\vec{c}|=2\),①
\(\therefore \dfrac{c^{2}}{a b+1}=\dfrac{\vec{a} \cdot \vec{b}+(\vec{a}-\vec{b}) \cdot \vec{c}+3}{a b+1}\),②
将①两边平方得 \((\vec{a}-\vec{b})^{2}+\vec{c}^{2}-2(\vec{a}-\vec{b}) \cdot \vec{c}=4\),
\(\therefore(\vec{a}-\vec{b})^{2}+\vec{c}^{2}-4=2(\vec{a}-\vec{b}) \cdot \vec{c}\),
\(\therefore \dfrac{(\vec{a}-\vec{b})^{2}}{2}+\dfrac{\vec{c}^{2}}{2}-2=(\vec{a}-\vec{b}) \cdot \vec{c}\),
代入②中,得 \(\dfrac{c^{2}}{a b+1}=\dfrac{\vec{a} \cdot \vec{b}+\dfrac{(\vec{a}-\vec{b})^{2}}{2}+\dfrac{\vec{c}^{2}}{2}+1}{a b+1}\),
\(\therefore \dfrac{1}{2} \vec{c}^{2}=\vec{a} \cdot \vec{b}+1+\dfrac{(\vec{a}-\vec{b})^{2}}{2}=\vec{a} \cdot \vec{b}+1+\dfrac{1}{2}\left(\vec{a}^{2}+\vec{b}^{2}-2 \vec{a} \cdot \vec{b}\right)\)
\(=1+\dfrac{1}{2}\left(\vec{a}^{2}+\vec{b}^{2}\right)\),
\(\therefore \vec{c}^{2}=2+\vec{a}^{2}+\vec{b}^{2}\),
又 \(\overrightarrow{c^{2}}=c^{2}, \vec{a}^{2}=a^{2}, \vec{b}^{2}=b^{2}\),
\(\therefore \dfrac{c^{2}}{a b+1}=\dfrac{2+a^{2}+b^{2}}{a b+1} \geq \dfrac{2+2 a b}{a b+1}=2\).
\(\therefore \dfrac{c^{2}}{a b+1}\)的最小值为\(2\).


 浙公网安备 33010602011771号
浙公网安备 33010602011771号