1.1.1 空间向量及其线性运算
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
【基础过关系列】 高二数学上学期同步知识点剖析精品讲义(人教A版2019)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
选择性必修第一册同步巩固,难度2颗星!
基础知识
空间向量的概念
在空间,我们把具有大小和方向的量叫做空间向量,用字母 \(\vec{a}, \vec{b}, \vec{c}\)……表示,空间向量的大小叫做空间向量的长度或模.
解释
(1) 空间中点的位移、物体运动的速度、物体受到的力等都可以用空间向量表示;
(2) 向量\(\vec{a}\)的起点是\(A\),终点是\(B\),则向量\(\vec{a}\)也可以记作\(\overrightarrow{A B}\),其模记为\(|\vec{a}|\)或\(|\overrightarrow{A B}|\);
(3) 向量一般用有向线段表示 同向等长的有向线段表示同一或相等的向量;
(4) 向量具有平移不变性.
(5) 在空间,零向量、单位向量、相等向量、反向量与在平面的对应向量一样.
【例】下列说法中正确的是( ).
A.单位向量都相等
B.任一向量与它的相 反向量不相等
C.若\(|\vec{a}|=|\vec{b}|\),则\(\vec{a}\)与\(\vec{b}\)的长度相等,方向相同或相反
D.若\(\vec{a}\)与\(\vec{b}\)是相反向量,则\(|\vec{a}|=|\vec{b}|\)
解析 对于\(A\),单位向量的模相等,但是方向不一定一样,故\(A\)错;
对于\(B\),零向量与其反向量相等;
对于\(C\),\(|\vec{a}|=|\vec{b}|\)只能说明两向量的模相等,方向可以是多样的,故\(C\)错;
对于\(D\),相反向量的模是相等的,故\(D\)是正确的.故选\(D\).
【练】给出下列命题:
①若空间向量\(\vec{a},\vec{b}\)满足\(|\vec{a}|=|\vec{b}|\),则\(\vec{a}=\vec{b}\);
②若空间向量\(\vec{m},\vec{n},\vec{p}\)满足\(\vec{m}=\vec{n}\),\(\vec{n}=\vec{p}\),则\(\vec{m}=\vec{p}\);
③零向量没有方向;
④若两个空间向量相等,则它们的起点 相同,终点也相同.
其中假命题的个数是( ).
A.\(1\) \(\qquad \qquad\) B.\(2\) \(\qquad \qquad\)C.\(3\) \(\qquad \qquad\) D.\(4\)
解析 对于①,向量方向不相同,则\(\vec{a}≠\vec{b}\),故①错;
对于②,空间向量也具有传递性,故②正确;
对于③,零向量的方向是任意的,故③错;
对于④,相等向量的起点与终点不一定相同,故④错.故选\(C\).
运算
(1) 定义 与平面向量运算一样,空间向量的加法、减法与数乘运算如下(如图).

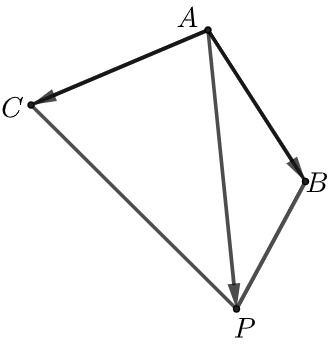
\(\overrightarrow{OA} = \overrightarrow{OB} + \overrightarrow{OC}=\vec{a}+\vec{b}\), \(\overrightarrow{CB} = \overrightarrow{OB}- \overrightarrow{OC} =\vec{a}-\vec{b}\), \(\overrightarrow{OP}=λ\vec{a} (λ\in R)\)
(2) 运算律
① 加法交换律:\(\vec{a}+\vec{b}=\vec{b} +\vec{a}\);
② 加法结合律:\((\vec{a}+\vec{b})+\vec{c} =\vec{a}+(\vec{b} +\vec{c})\);
③ 数乘分配律:\(λ(\vec{a}+\vec{b})=λ\vec{a}+λ\vec{b}\);
运算法则:三角形法则、平行四边形法则、平行六面体法则.
注 平行六面体法则: 在平行六面体\(ABCD-A_1 B_1 C_1 D_1\)中,\(\overrightarrow{A C_{1}}=\overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{A A_{1}}\).

【例】已知空间四边形\(ABCD\)中,\(\overrightarrow{AB} =\vec{a}\),\(\overrightarrow{CB} =\vec{b}\), \(\overrightarrow{AD} =\vec{c}\) ,则 \(\overrightarrow{CD}\)等于( ).
A.\(\vec{a}+\vec{b}-\vec{c}\) \(\qquad \qquad\) B.\(-\vec{a}-\vec{b}+\vec{c}\) \(\qquad \qquad\) C.\(-\vec{a}+\vec{b}+\vec{c}\) \(\qquad \qquad\) D.\(-\vec{a}+\vec{b}-\vec{c}\)
解析 \(\overrightarrow{C D}=\overrightarrow{C B}+\overrightarrow{B A}+\overrightarrow{A D}=\vec{b}-\vec{a}+\vec{c}=-\vec{a}+\vec{b}+\vec{c}\),故选\(C\).

【练】化简 \((\overrightarrow{A B}-\overrightarrow{C D})-(\overrightarrow{A C}-\overrightarrow{B D})\).
解析 \((\overrightarrow{A B}-\overrightarrow{C D})-(\overrightarrow{A C}-\overrightarrow{B D})=\overrightarrow{A B}-\overrightarrow{C D}-\overrightarrow{A C}+\overrightarrow{B D}=\overrightarrow{A B}+\overrightarrow{D C}+\overrightarrow{C A}+\overrightarrow{B D}=\overrightarrow{0}\).
共线向量
1 如果表示空间向量的有向线段所在的直线平行或重合,那么这些向量也叫做共线向量或平行向量,\(\vec{a}\)平行于\(\vec{b}\),记作\(\vec{a}//\vec{b}\).
2 共线向量定理:空间任意两个向量\(\vec{a}\),\(\vec{b}(\vec{b}≠\vec{0} )\), \(\vec{a}// \vec{b}⇒\)存在实数λ,使\(\vec{a}=λ\vec{b}\) .
3 三点共线:\(A、B、C\)三点共线 \(\Rightarrow \overrightarrow{A B}=\lambda \overrightarrow{A C}\);
4 与\(\vec{a}\)共线的单位向量为 \(\pm \dfrac{\vec{a}}{|\vec{a}|}\).
【例】 如图,在平行六面体\(ABCD-A'B'C'D'\)中,\(E,F\)分别是\(BD,BC'\)的中点,判断以下向量是否共线向量,若是,则判断是同向向量还是反向向量:① \(\overrightarrow{A B}\)与\(\overrightarrow{D'C'}\); ②\(\overrightarrow{A D}\) 与\(\overrightarrow{BC'}\) ;③\(\overrightarrow{EF}\)与\(\overrightarrow{C'D}\) ;④\(\overrightarrow{AD'}\)与\(\overrightarrow{C'B}\) ;

解析 ① \(\overrightarrow{A B}=\overrightarrow{D^{\prime} C^{\prime}}\),\(\overrightarrow{A B}\)与\(\overrightarrow{D'C'}\)是同向向量;②\(AD\)与\(BC'\)是异面直线,\(\overrightarrow{A D}\) 与\(\overrightarrow{BC'}\)不是共线向量;
③\(EF//C' D\)且 \(E F=\dfrac{1}{2} C^{\prime} D\),则 \(\overrightarrow{E F}=-\dfrac{1}{2} \overrightarrow{C^{\prime} D}\),则\(\overrightarrow{EF}\)与\(\overrightarrow{C'D}\) 是反向向量;
④ \(\overrightarrow{A D^{\prime}}=-\overrightarrow{C^{\prime} B}\),\(\overrightarrow{AD'}\)与\(\overrightarrow{C'B}\) 是反向向量.
【练】已知向量\(\vec{a}\),\(\vec{b}\)且 \(\overrightarrow{A B}=\vec{a}+2 \vec{b}\), \(\overrightarrow{B C}=-5 \vec{a}+6 \vec{b}\), \(\overrightarrow{C D}=7 \vec{a}-2 \vec{b}\),则一定共线的三点为( ).
A.\(A,B,D\) \(\qquad \qquad\) B.\(A,B,C\) \(\qquad \qquad\) C.\(B,C,D\) \(\qquad \qquad\) D.\(A,C,D\)
解析 因为 \(\overrightarrow{B D}=\overrightarrow{B C}+\overrightarrow{C D}=-5 \vec{a}+6 \vec{b}+7 \vec{a}-2 \vec{b}=2 \vec{a}+4 \vec{b}=2 \overrightarrow{A B}\),
所以 \(\overrightarrow{A B}\)与 \(\overrightarrow{ BD}\)共线,即\(A,B,D\)三点共线.
共面向量
1 定义
一般地,能平移到同一平面内的向量叫做共面向量.说明:空间任意的两向量都是共面的.
2 共面向量定理
如果两个向量\(\vec{a}\),\(\vec{b}\)不共线,\(\vec{p}\)与向量\(\vec{a}\),\(\vec{b}\)共面的充要条件是存在唯一实数对\((x ,y)\),使\(\vec{p}=x\vec{a}+y\vec{b}\).
3 四点共面
方法1 若要证明\(A、B、C、P\)四点共面,只需要证明 \(\overrightarrow{A P}, \overrightarrow{A B}, \overrightarrow{A C}\)共面,即 \(\overrightarrow{A P}=x \overrightarrow{A B}+y \overrightarrow{A C}\).
方法2 若要证明\(A、B、C、P\)四点共面,只需要证明 \(\overrightarrow{O P}=x \overrightarrow{O A}+y \overrightarrow{O B}+z \overrightarrow{O C}\)(其中\(x+y+z=1\))
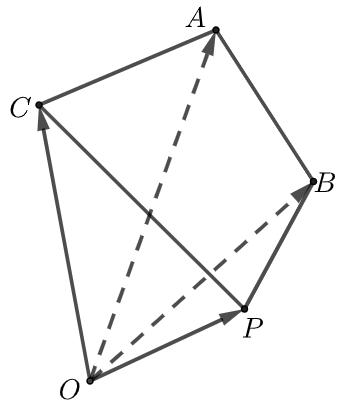
证明 若\(x+y+z=1\),
则 \(\overrightarrow{O P}=x \overrightarrow{O A}+y \overrightarrow{O B}+z \overrightarrow{O C}=x \overrightarrow{O A}+y \overrightarrow{O B}+(1-x-y) \overrightarrow{O C}\)
\(=\overrightarrow{O C}+x(\overrightarrow{O A}-\overrightarrow{O C})+y(\overrightarrow{O B}-\overrightarrow{O C})=\overrightarrow{O C}+x \overrightarrow{C A}+y \overrightarrow{C B}\),
\(\therefore \overrightarrow{O P}-\overrightarrow{O C}=x \overrightarrow{C A}+y \overrightarrow{C B}\), \(\therefore \overrightarrow{C P}=x \overrightarrow{C A}+y \overrightarrow{C B}\),
即 \(\overrightarrow{C P}, \overrightarrow{C A}, \overrightarrow{C B}\)共面,即\(A、B、C、P\)四点共面.
【例】在下列条件中,使\(M\)与\(A,B,C\)一定共面的是( )
A. \(\overrightarrow{O M}=\overrightarrow{O A}-\overrightarrow{O B}-\overrightarrow{O C}\) \(\qquad \qquad\) B. \(\overrightarrow{O M}=\dfrac{1}{5} \overrightarrow{O A}+\dfrac{1}{3} \overrightarrow{O B}+\dfrac{1}{2} \overrightarrow{O C}\)
C. \(\overrightarrow{M A}+\overrightarrow{M B}+\overrightarrow{M C}=\overrightarrow{0}\) \(\qquad \qquad\) D. \(\overrightarrow{O M}+\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}=\overrightarrow{0}\)
解析 在\(C\)中,由 \(\overrightarrow{M A}+\overrightarrow{M B}+\overrightarrow{M C}=\overrightarrow{0}\),得 \(\overrightarrow{M A}=-\overrightarrow{M B}-\overrightarrow{M C}\),
则 \(\overrightarrow{M A}, \overrightarrow{M B}, \overrightarrow{M C}\)为共面向量,即\(M、A、B、C\)四点共面;
对于\(A\),由 \(\overrightarrow{O M}=\overrightarrow{O A}-\overrightarrow{O B}-\overrightarrow{O C}\),得\(1-1-1=-1≠1\),
不能得出\(M、A、B、C\)四点共面;
对于\(B\),由 \(\overrightarrow{O M}=\dfrac{1}{5} \overrightarrow{O A}+\dfrac{1}{3} \overrightarrow{O B}+\dfrac{1}{2} \overrightarrow{O C}\),得 \(\dfrac{1}{5}+\dfrac{1}{3}+\dfrac{1}{2} \neq 1\),
所以\(M、A、B、C\)四点不共面;
对于\(D\),由 \(\overrightarrow{O M}+\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}=\overrightarrow{0}\),得 \(\overrightarrow{O M}=-(\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C})\),
其系数和不为\(1\),所以\(M、A、B、C\)四点不共面.
故选:\(C\).
【练1】 下列说法中正确的是( ).
A.平面内的任意两个向量都共线 \(\qquad \qquad\) B.空间的任意三个向量都不共面 \(\qquad \qquad\)
C.空间的任意两个向量都共面 \(\qquad \qquad\) D.空间的任意三个向量都共面
答案 \(C\)
【练2】 \(O\)为空间中任意一点,\(A,B,C\)三点不共线,且 \(\overrightarrow{O P}=\dfrac{3}{4} \overrightarrow{O A}+\dfrac{1}{8} \overrightarrow{O B}+t \overrightarrow{O C}\),若\(P,A,B,C\)四点共面,则实数\(t=\) .
解析 由题意得, \(\overrightarrow{O P}=\dfrac{3}{4} \overrightarrow{O A}+\dfrac{1}{8} \overrightarrow{O B}+t \overrightarrow{O C}\),且\(P,A,B,C\)四点共面,
\(\therefore \dfrac{3}{4}+\dfrac{1}{8}+t=1\), \(\therefore t=\dfrac{1}{8}\).
基本方法
【题型1】空间向量的线性运算
【典题1】 在平行六面体\(ABCD-A_1 B_1 C_1 D_1\)中,\(M\)为\(A_1 C_1\)与\(B_1 D_1\)的交点,若 \(\overrightarrow{A B}=\vec{a}, \overrightarrow{A D}=\vec{b}, \overrightarrow{A A_{1}}=\vec{c}\),则与 \(\overrightarrow{ BM}\)相等的向量是( )

A. \(\dfrac{1}{2} \vec{a}+\dfrac{1}{2} \vec{b}+\vec{c}\) \(\qquad \qquad\) B.\(-\dfrac{1}{2} \vec{a}+\dfrac{1}{2} \vec{b}+\vec{c}\) \(\qquad \qquad\) C.\(\dfrac{1}{2} \vec{a}-\dfrac{1}{2} \vec{b}+\vec{c}\) \(\qquad \qquad\) D. \(-\dfrac{1}{2} \vec{a}-\dfrac{1}{2} \vec{b}+\vec{c}\)
解析 在平行六面体\(ABCD-A_1 B_1 C_1 D_1\)中,\(M\)为\(A_1 C_1\)与\(B_1 D_1\)的交点,\(\overrightarrow{A B}=\vec{a}, \overrightarrow{A D}=\vec{b}, \overrightarrow{A A_{1}}=\vec{c}\),
\(\therefore \overrightarrow{B M}=\overrightarrow{B B_{1}}+\overrightarrow{B_{1} M}=\overrightarrow{A A_{1}}+\dfrac{1}{2} \overrightarrow{B D}=\overrightarrow{A A_{1}}+\dfrac{1}{2}(\overrightarrow{B A}+\overrightarrow{B C})\)
\(=-\dfrac{1}{2} \overrightarrow{A B}+\dfrac{1}{2} \overrightarrow{A D}+\overrightarrow{A A_{1}}=-\dfrac{1}{2} \vec{a}+\dfrac{1}{2} \vec{b}+\vec{c}\).
故选:\(B\).
巩固练习
1.空间中 任意四个点\(A,B,C,D\),则 \(\overrightarrow{D A}+\overrightarrow{C D}-\overrightarrow{C B}\)等于( ).
A. \(\overrightarrow{DB}\) \(\qquad \qquad\) B. \(\overrightarrow{AC}\) \(\qquad \qquad\) C. \(\overrightarrow{AB}\) \(\qquad \qquad\) D. \(\overrightarrow{BA}\)
2.已知三棱锥\(A-BCD\)中,\(E\)是\(BC\)的中点,则 \(\overrightarrow{A E}-\dfrac{1}{2}(\overrightarrow{A C}+\overrightarrow{A D})=\)( )
A. \(\overrightarrow{BD }\) \(\qquad \qquad\) B. \(\overrightarrow{DB }\) \(\qquad \qquad\) C. \(\dfrac{1}{2} \overrightarrow{B D}\) \(\qquad \qquad\) D. \(\dfrac{1}{2} \overrightarrow{D B}\)
3.如图,在四面体\(ABCD\)中,\(E,F,G,H\)分别为\(AB,BC,CD,AC\)的中点,则 \(\dfrac{1}{2}(\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C D})=\) ( )

A. \(\overrightarrow{ BF}\) \(\qquad \qquad\) B. \(\overrightarrow{EH}\) \(\qquad \qquad\) C. \(\overrightarrow{FG}\) \(\qquad \qquad\) D. \(\overrightarrow{HG}\)
4 如图,在三棱锥\(S-ABC\)中,点\(E,F\)分别是\(SA,BC\)的中点,点\(G\)在棱\(EF\)上,且满足 \(\dfrac{E G}{G F}=\dfrac{1}{2}\),若 \(\overrightarrow{S A}=\vec{a}\), \(\overrightarrow{S B}=\vec{b}\), \(\overrightarrow{S C}=\vec{c}\),则 \(\overrightarrow{SG} =\)( )

A. \(\dfrac{1}{3} \vec{a}-\dfrac{1}{2} \vec{b}+\dfrac{1}{6} \vec{c}\) \(\qquad \qquad\) B. \(\dfrac{1}{3} \vec{a}+\dfrac{1}{6} \vec{b}+\dfrac{1}{6} \vec{c}\) \(\qquad \qquad\) C. \(\dfrac{1}{6} \vec{a}-\dfrac{1}{3} \vec{b}+\dfrac{1}{2} \vec{c}\) \(\qquad \qquad\) D. \(\dfrac{1}{3} \vec{a}-\dfrac{1}{6} \vec{b}+\dfrac{1}{2} \vec{c}\)
参考答案
-
答案 \(D\)
解析 \(\overrightarrow{D A}+\overrightarrow{C D}-\overrightarrow{C B}=(\overrightarrow{C D}+\overrightarrow{D A})-\overrightarrow{C B}=\overrightarrow{C A}-\overrightarrow{C B}=\overrightarrow{B A}\). -
答案 \(D\)
解析 如图,取\(CD\)中点\(F\),连结\(AF\),\(EF\),
\(∵\)三棱锥\(A-BCD\)中,\(E\)是\(BC\)的中点,
\(\therefore \overrightarrow{A E}-\dfrac{1}{2}(\overrightarrow{A C}+\overrightarrow{A D})=\overrightarrow{A E}-\overrightarrow{A F}=\overrightarrow{F E}=\dfrac{1}{2} \overrightarrow{D B}\).
故选:\(D\).

-
答案 \(D\)
解析 如图所示:

取\(AD\)的中点\(K\),由于 \(\dfrac{1}{2} \overrightarrow{A B}=\overrightarrow{A E}\), \(\dfrac{1}{2} \overrightarrow{B C}=\overrightarrow{E H}\),
所以 \(\dfrac{1}{2}(\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C D})=\overrightarrow{A E}+\overrightarrow{E H}+\overrightarrow{C G}=\overrightarrow{H C}+\overrightarrow{C G}=\overrightarrow{H G}\)
故选:\(D\). -
答案 \(B\)
解析 因为 \(\overrightarrow{S G}=\overrightarrow{S E}+\overrightarrow{E G}=\dfrac{1}{2} \overrightarrow{S A}+\dfrac{1}{3} \overrightarrow{E F}=\dfrac{1}{2} \overrightarrow{S A}+\dfrac{1}{3}(\overrightarrow{E S}+\overrightarrow{S C}+\overrightarrow{C F})\),
\(=\dfrac{1}{2} \overrightarrow{S A}+\dfrac{1}{6} \overrightarrow{A S}+\dfrac{1}{3} \overrightarrow{S C}+\dfrac{1}{6} \overrightarrow{C B}=\dfrac{1}{3} \overrightarrow{S A}+\dfrac{1}{3} \overrightarrow{S C}+\dfrac{1}{6}(\overrightarrow{C S}+\overrightarrow{S B})\)
\(=\dfrac{1}{3} \overrightarrow{S A}+\dfrac{1}{6} \overrightarrow{S B}+\dfrac{1}{6} \overrightarrow{S C}=\dfrac{1}{3} \vec{a}+\dfrac{1}{6} \vec{b}+\dfrac{1}{6} \vec{c}\).
故选:\(B\).
【题型2】 空间向量共线问题
【典题1】对于空间任意一点\(O\),以下条件可以判定点\(P,A,B\)共线的是\(\underline{\quad \quad}\) (填序号).
①\(\overrightarrow{O P}=\overrightarrow{O A}+t \overrightarrow{A B}(t \in R, t \neq 0)\); ② \(5 \overrightarrow{O P}=\overrightarrow{O A}+\overrightarrow{A B}\);
③ \(\overrightarrow{O P}=\overrightarrow{O A}-t \overrightarrow{A B}(t \in R, t \neq 0)\); ④ \(\overrightarrow{O P}=-\overrightarrow{O A}+\overrightarrow{A B}\).
解析 对于①,\(∵\overrightarrow{O P}=\overrightarrow{O A}+t \overrightarrow{A B}(t \in R, t \neq 0)\),
\(\therefore \overrightarrow{O P}-\overrightarrow{O A}=t \overrightarrow{A B}(t \neq 0)\), \(\therefore \overrightarrow{A P}=t \overrightarrow{A B}(t \neq 0)\),
\(∴\)点\(P、A、B\)共线,故①正确;
对于②, \(\because 5 \overrightarrow{O P}=\overrightarrow{O A}+\overrightarrow{A B}\), \(\therefore 5 \overrightarrow{O P}=\overrightarrow{O B}\), \(\therefore \overrightarrow{O P}, \overrightarrow{O B}\)共线,
\(∴P,O,B\)共线,点\(P,A,B\)不一定共线,故②错误;
对于③, \(\because \overrightarrow{O P}=\overrightarrow{O A}+\overrightarrow{A B}(t \neq 0)\), \(\therefore \overrightarrow{O P}-\overrightarrow{O A}=-t \overrightarrow{A B}(t \neq 0)\),
\(\therefore \overrightarrow{A P}=-t \overrightarrow{A B}(t \neq 0)\), \(\therefore \overrightarrow{A P}, \overrightarrow{A B}\)共线,\(∴P,A,B\)共线,故③正确;
对于④, \(\because \overrightarrow{O P}=-\overrightarrow{O A}+\overrightarrow{A B}\), \(\therefore \overrightarrow{O P}=-\overrightarrow{O A}+\overrightarrow{O B}-\overrightarrow{O A}\),
\(\therefore \overrightarrow{O P}=-2 \overrightarrow{O A}+\overrightarrow{O B}\), \(\therefore \overrightarrow{O P}-\overrightarrow{O B}=-2 \overrightarrow{O A}\),
\(\therefore \overrightarrow{B P}=-2 \overrightarrow{O A}\),\(∴BP,OA\)平行或重合,
故\(BP,OA\)平行时,点\(P,A,B\)不共线,故④错误.
故选:①③.
【典题2】如图,在正方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(E\)在\(A_1 D_1\)上,且 \(\overrightarrow{A_{1} E}=2 \overrightarrow{E D_{1}}\),\(F\)在对角线\(A_1 C\)上,且 \(\overrightarrow{A_{1} F}=\dfrac{2}{3} \overrightarrow{F C}\).若 \(\overrightarrow{A B}=\vec{a}, \overrightarrow{A D}=\vec{b}, \overrightarrow{A A_{1}}=\vec{c}\).
(1)用 \(\vec{a}, \vec{b}, \vec{c}\)表示 \(\overrightarrow{EB}\);(2)求证:\(E,F,B\)三点共线.

解析 (1) \(\overrightarrow{E B}=\overrightarrow{E A_{1}}+\overrightarrow{A_{1} A}+\overrightarrow{A B}=\dfrac{2}{3} \overrightarrow{D A}-\overrightarrow{A A_{1}}+\overrightarrow{A B}=\vec{a}-\vec{c}-\dfrac{2}{3} \vec{b}\),
证明:(2)设 \(\overrightarrow{A B}=\vec{a}, \overrightarrow{A D}=\vec{b}, \overrightarrow{A A_{1}}=\vec{c}\),
\(\because \overrightarrow{A_{1} E}=2 \overrightarrow{E D_{1}}\),\(\overrightarrow{A_{1} F}=\dfrac{2}{3} \overrightarrow{F C}\) ,\(\therefore \overrightarrow{A_{1} E}=\dfrac{2}{3} \overrightarrow{A_{1} D_{1}}, \overrightarrow{A_{1} F}=\dfrac{2}{5} \overrightarrow{A_{1} C}\),
\(\therefore \overrightarrow{A_{1} E}=\dfrac{2}{3} \overrightarrow{A D}=\dfrac{2}{3} \vec{b}\), \(\overrightarrow{A_{1} F}=\dfrac{2}{5}\left(\overrightarrow{A C}-\overrightarrow{A A_{1}}\right)=\dfrac{2}{5}\left(\overrightarrow{A B}+\overrightarrow{A D}-\overrightarrow{A A_{1}}\right)=\dfrac{2}{5} \vec{a}+\dfrac{2}{5} \vec{b}-\dfrac{2}{5} \vec{c}\),
\(\therefore \overrightarrow{E F}=\overrightarrow{A_{1} F}-\overrightarrow{A_{1} E}=\dfrac{2}{5} \vec{a}-\dfrac{4}{15} \vec{b}-\dfrac{2}{5} \vec{c}=\dfrac{2}{5}\left(\vec{a}-\dfrac{2}{3} \vec{b}-\vec{c}\right)\),
又\(∵\)由(1)知 \(\overrightarrow{E B}=\vec{a}-\vec{c}-\dfrac{2}{3} \vec{b}\),
\(\therefore \overrightarrow{E F}=\dfrac{2}{5} \overrightarrow{E B}\),且有公共点\(E\),
\(∴E,F,B\)三点共线.
巩固练习
1.如图,在平行六面体\(ABCD-A_1 B_1 C_1 D_1\)中,\(M,N\)分别是\(C_1 D_1\),\(AB\)的中点,\(E\)在\(AA_1\)上且
\(AE=2EA_1\),\(F\)在\(CC_1\)上且 \(C F=\dfrac{1}{2} F C_{1}\),判断 \(\overrightarrow{M E}\)与 \(\overrightarrow{NF}\)是否共线?

2.如图,四边形\(ABCD\)和\(ABEF\)都是平行四边形,且不共面,\(M\),\(N\)分别是\(AC\),\(BF\)的中点.判断 \(\overrightarrow{CE}\)与 \(\overrightarrow{MN }\)是否共线.

参考答案
-
答案 共线
解析 由已知可得: \(\overrightarrow{M E}=\overrightarrow{M D_{1}}+\overrightarrow{D_{1} A_{1}}+\overrightarrow{A_{1} E}\)
\(=\dfrac{1}{2} \overrightarrow{B A}+\overrightarrow{C B}+\dfrac{1}{3} \overrightarrow{A_{1} A}=-\overrightarrow{N B}+\overrightarrow{C B}+\dfrac{1}{3} \overrightarrow{C_{1} C}=\overrightarrow{C N}+\overrightarrow{F C}\)\(=\overrightarrow{F N}=-\overrightarrow{N F}\).
所以 \(\overrightarrow{M E}=-\overrightarrow{N F}\),故 \(\overrightarrow{M E}\)与 \(\overrightarrow{NF}\)共线. -
答案 共线
解析 \(∵M,N\)分别是\(AC\),\(BF\)的中点,而四边形\(ABCD\),\(ABEF\)都是平行四边形,
\(\therefore \overrightarrow{M N}=\overrightarrow{M A}+\overrightarrow{A F}+\overrightarrow{F N}=\dfrac{1}{2} \overrightarrow{C A}+\overrightarrow{A F}+\dfrac{1}{2} \overrightarrow{F B}\).
又 \(\because \overrightarrow{M N}=\overrightarrow{M C}+\overrightarrow{C E}+\overrightarrow{E B}+\overrightarrow{B N}=-\dfrac{1}{2} \overrightarrow{C A}+\overrightarrow{C E}-\overrightarrow{A F}-\dfrac{1}{2} \overrightarrow{F B}\),
\(\therefore \dfrac{1}{2} \overrightarrow{C A}+\overrightarrow{A F}+\dfrac{1}{2} \overrightarrow{F B}=-\dfrac{1}{2} \overrightarrow{C A}+\overrightarrow{C E}-\overrightarrow{A F}-\dfrac{1}{2} \overrightarrow{F B}\).
\(\therefore \overrightarrow{C E}=\overrightarrow{C A}+2 \overrightarrow{A F}+\overrightarrow{F B}=2(\overrightarrow{M A}+\overrightarrow{A F}+\overrightarrow{F N})=2 \overrightarrow{M N}\),
\(\therefore \overrightarrow{C E} / / \overrightarrow{M N}\),即 \(\overrightarrow{CE}\)与 \(\overrightarrow{MN }\)共线.
【题型3】 空间向量共面问题
【典题1】下面关于空间向量的说法正确的是( ).
A.若向量\(\vec{a}\),\(\vec{b}\)平行,则\(\vec{a}\),\(\vec{b}\)所在的直线平行
B.若向量\(\vec{a}\),\(\vec{b}\)所在直线是异面直线,则\(\vec{a}\),\(\vec{b}\)不共面
C.若\(A,B,C,D\)四点不共面,则向量 \(\overrightarrow{A B}, \overrightarrow{CD}\)不共面
D.若\(A,B,C,D\)四点不共面,则向量 \(\overrightarrow{A B}, \overrightarrow{A C}, \overrightarrow{A D}\)不共面
解析可以通过平移将空间中任意两个向量平移到一个平面内,因此空间任意两个向量都是共面的,故\(B,C\)都不正确.注意向量平行与直线平行的区别,可知\(A\)不正确,可用反证法证明\(D\)是正确的.
【典题2】如图所示,已知斜三棱柱\(ABC-A_1 B_1 C_1\),点\(M\),\(N\)分别在\(AC_1\)和\(BC\)上,且满足 \(\overrightarrow{A M}=k \overrightarrow{A C_{1}}\), \(\overrightarrow{B N}=k \overrightarrow{B C}(0 \leqslant k \leqslant 1)\),判断向量 \(\overrightarrow{MN}\)是否与向量 \(\overrightarrow{A B}, \overrightarrow{A A_{1}}\)共面.
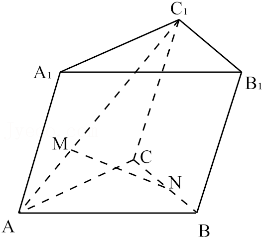
解析 \(\because \overrightarrow{A N}=\overrightarrow{A B}+\overrightarrow{B N}=\overrightarrow{A B}+k(\overrightarrow{A C}-\overrightarrow{A B})=(1-k) \overrightarrow{A B}+k \overrightarrow{A C}\).
\(\overrightarrow{A M}=k \overrightarrow{A C_{1}}=k\left(\overrightarrow{A A_{1}}+\overrightarrow{A C}\right)\),\(\therefore \overrightarrow{M N}=\overrightarrow{A N}-\overrightarrow{A M}=(1-k) \overrightarrow{A B}-k \overrightarrow{A A_{1}}\),
\(∴\)向量\(\overrightarrow{MN}\)与向量 \(\overrightarrow{A B}, \overrightarrow{A A_{1}}\)共面.
【典题3】 如图所示,已知平行四边形\(ABCD\),从平面\(AC\)外一点\(O\)引向量 \(\overrightarrow{O E}=k \overrightarrow{O A}\), \(\overrightarrow{O F}=k \overrightarrow{O B}\), \(\overrightarrow{O G}=k \overrightarrow{O C}\), \(\overrightarrow{O H}=k \overrightarrow{O D}\),求证:
(1)四点\(E,F,G,H\)共面;(2)平面\(AC∥\)平面\(EG\).

证明 (1)因为四边形\(ABCD\)是平行四边形,
所以 \(\overrightarrow{A C}=\overrightarrow{A B}+\overrightarrow{A D}, \overrightarrow{E G}=\overrightarrow{O G}-\overrightarrow{O E}=k \overrightarrow{O C}-k \overrightarrow{O A}=k \overrightarrow{A C}=k(\overrightarrow{A B}+\overrightarrow{A D})\)\(=k(\overrightarrow{O B}-\overrightarrow{O A}+\overrightarrow{O D}-\overrightarrow{O A})=\overrightarrow{O F}-\overrightarrow{O E}+\overrightarrow{O H}-\overrightarrow{O E}=\overrightarrow{E F}+\overrightarrow{E H}\).
所以\(E,F,G,H\)共面.
(2) \(\overrightarrow{E F}=\overrightarrow{O F}-\overrightarrow{O E}=k(\overrightarrow{O B}-\overrightarrow{O A})=k \overrightarrow{A B}\),且由第 (1)小题的证明中知 \(\overrightarrow{E G}=k \overrightarrow{A C}\),
于是\(EF∥AB\),\(EG∥AC\).所以平面\(EG∥\)平面\(AC\).
巩固练习
1.(多选)在以下命题中,不正确的命题有( )
A.若\(\vec{a}\)与 \(\vec{b}\)共线,\(\vec{b}\)与\(\vec{c}\)共线,则\(\vec{a}\)与\(\vec{c}\)共线
B.若\(\vec{a}//\vec{b}\),则存在唯一的实数\(λ\),使\(\vec{a}=λ\vec{b}\)
C.对空间任意一点\(O\)和不共线的三点\(A,B,C\),若 \(\overrightarrow{O P}=2 \overrightarrow{O A}+2 \overrightarrow{O B}-3 \overrightarrow{O C}\),则\(P,A,B,C\)四点共面
D.若两个非零空间向量 \(\overrightarrow{A B}, \overrightarrow{C D}\)满足 \(\overrightarrow{A B}+\overrightarrow{C D}=\overrightarrow{0}\),则 \(\overrightarrow{A B} / / \overrightarrow{C D}\)
2.对于空间任意一点\(O\)和不共线得三点\(A,B,C\),有如下关系: \(\overrightarrow{O P}=\dfrac{1}{6} \overrightarrow{O A}+\dfrac{1}{3} \overrightarrow{O B}+\dfrac{1}{2} \overrightarrow{O C}\),则( )
A.四点\(O,A,B,C\)必共面 \(\qquad \qquad\) B.四点\(P,A,B,C\)必共面
C.四点\(O,P,B,C\)必共面 \(\qquad \qquad\) D.五点\(O,P,A,B,C\)必共面
3.已知三个向量 \(\vec{a}, \vec{b}, \vec{c}\)不共面,且 \(\vec{p}=\vec{a}+\vec{b}-\vec{c}\), \(\vec{q}=2 \vec{a}-3 \vec{b}-5 \vec{c}\), \(\vec{r}=-7 \vec{a}+18 \vec{b}+22 \vec{c}\).试问向量 \(\vec{p}, \vec{q}, \vec{r}\)是否共面.
4.已知\(E,F,G,H\)分别是空间四边形\(ABCD\)的边\(AB,BC,CD,DA\)的中点,用向量法证明:\(E,F,G,H\)四点共面.

参考答案
-
答案 \(AB\)
解析 当 \(\vec{b}=\overrightarrow{0}\),满足\(\vec{a}\)与 \(\vec{b}\)共线,\(\vec{b}\)与\(\vec{c}\)共线,而\(\vec{a}\)与\(\vec{c}\)不一定共线,故\(A\)错误;
当\(\vec{a}\)与 \(\vec{b}\)均为零向量时,能够保证 \(\vec{a}//\vec{b}\),则存在无数多的实数\(λ\),
使得 \(\vec{a}=λ\vec{b}\),故 \(B\)错误;
\(\because \overrightarrow{O P}=2 \overrightarrow{O A}+2 \overrightarrow{O B}-3 \overrightarrow{O C}\),即 \(\overrightarrow{O P}-\overrightarrow{O A}=(\overrightarrow{O A}-\overrightarrow{O C})+2(\overrightarrow{O B}-\overrightarrow{O C})\),
\(\therefore \overrightarrow{A P}=\overrightarrow{C A}+2 \overrightarrow{C B}\),
由平面向量基本定理可得\(P,A,B,C\)四点共面,故\(C\)正确;
\(∵\)非零空间向量\(\overrightarrow{A B}, \overrightarrow{C D}\)满足 \(\overrightarrow{A B}+\overrightarrow{C D}=\overrightarrow{0}\), \(\therefore \overrightarrow{A B}=-\overrightarrow{C D}\), \(\therefore \overrightarrow{A B} / / \overrightarrow{C D}\),故\(D\)正确.
故选:\(AB\). -
答案 \(B\)
解析 由 \(\overrightarrow{O P}=\dfrac{1}{6} \overrightarrow{O A}+\dfrac{1}{3} \overrightarrow{O B}+\dfrac{1}{2} \overrightarrow{O C}\), \(\dfrac{1}{6}+\dfrac{1}{3}+\dfrac{1}{2}=1\),可得四点\(P,A,B,C\)必共面.故选:\(B\). -
答案 共面
解析 假设三个向量共面,则设出实数\(x,y\),使得 \(\vec{p}=x \vec{q}+y \vec{r}\),
则 \(\vec{a}+\vec{b}-\vec{c}=x(2 \vec{a}-3 \vec{b}-5 \vec{c})+y(-7 \vec{a}+18 \vec{b}+22 \vec{c})\),
所以 \(\left\{\begin{array}{l} 1=2 x-7 y \\ 1=-3 x+18 y \\ -1=-5 x+22 y \end{array}\right.\),解得 \(\left\{\begin{array}{l} x=\dfrac{5}{3} \\ y=\dfrac{1}{3} \end{array}\right.\),
所以存在\(x,y\)值使得 \(\vec{p}=x \vec{q}+y \vec{r}\)成立,
所以向量 \(\vec{p}, \vec{q}, \vec{r}\)共面. -
证明 连结\(BG\),如图所示,
则 \(\overrightarrow{E G}=\overrightarrow{E B}+\overrightarrow{B G}=\overrightarrow{E B}+\overrightarrow{B F}+\overrightarrow{F G}=\overrightarrow{E B}+\overrightarrow{B F}+\dfrac{1}{2} \overrightarrow{B D}\)\(=\overrightarrow{E B}+\overrightarrow{B F}+\overrightarrow{E H}=\overrightarrow{E F}+\overrightarrow{E H}\),
由平面向量共面定理可知, \(\overrightarrow{E G}, \overrightarrow{E F}, \overrightarrow{E H}\)共面且它们有公共点\(E\),
所以\(E,F,G,H\)四点共面.

分层练习
【A组---基础题】
1下列说法正确的是( ).
A.向量\(\overrightarrow{AB}\)与\(\overrightarrow{BA}\)的长度相等
B.将空间中所有的单位向 量平移到同一起点,则它们的终点构成一个圆
C.空间向量就是空间中的一条有向线段
D.不相等的两个空间向量的模必不相等
2下列命题正确的是( ).
A.若\(\vec{a}\)与\(\vec{b}\)共线,\(\vec{b}\)与\(\vec{c}\)共线,则\(\vec{a}\)与\(\vec{c}\)共线
B.向量\(\vec{a},\vec{b},\vec{c}\)共面就是它们所在的直线共面
C.零向量没有确定的方向
D.若\(\vec{a}∥\vec{b}\),则存在唯一的实数\(λ\),使得\(\vec{a}=λ\vec{b}\)
3在正方体\(ABCD-A_1 B_1 C_1 D_1\)中,下列选项中化简后为零向量的是( ).
A. \(\overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{A A_{1}}\) \(\qquad \qquad\) B. \(\overrightarrow{A B}-\overrightarrow{A C}+\overrightarrow{B B_{1}}\)
C. \(\overrightarrow{A B}+\overrightarrow{A_{1} D_{1}}+\overrightarrow{C_{1} A_{1}}\) \(\qquad \qquad\) D. \(\overrightarrow{A C}+\overrightarrow{C B_{1}}-\overrightarrow{A B}\)
4当\(|\vec{a}|=|\vec{b}|≠0\),且\(\vec{a},\vec{b}\)不共线时,\(\vec{a}+\vec{b}\)与\(\vec{a}-\vec{b}\)的关系是( ).
A.共面 \(\qquad \qquad\) B.不共面 \(\qquad \qquad\) C.共线 \(\qquad \qquad\) D.无法确定
5如图所示,在四面体\(O-ABC\)中, \(\overrightarrow{O A}=\vec{a}, \overrightarrow{O B}=\vec{b}, \overrightarrow{O C}=\vec{c}\),点\(M\)在\(OA\)上,且 \(\overrightarrow{O M}=2 \overrightarrow{M A}\),\(N\)为\(BC\)的中点,则 \(\overrightarrow{M N}=\) ( )

A. \(\dfrac{1}{2} \vec{a}-\dfrac{2}{3} \vec{b}+\dfrac{1}{2} \vec{c}\) \(\qquad \qquad\) B. \(-\dfrac{2}{3} \vec{a}+\dfrac{1}{2} \vec{b}+\dfrac{1}{2} \vec{c}\) \(\qquad \qquad\) C. \(\dfrac{1}{2} \vec{a}+\dfrac{1}{2} \vec{b}-\dfrac{2}{3} \vec{c}\) \(\qquad \qquad\) D. \(\dfrac{2}{3} \vec{a}+\dfrac{2}{3} \vec{b}-\dfrac{1}{2} \vec{c}\)
6如图,\(\vec{a}\) , \(\vec{b}\)是两个空间向量,则 \(\overrightarrow{AC}\)与\(\overrightarrow{A'C'}\)是\(\underline{\quad \quad}\)向量, \(\overrightarrow{AB}\)与 \(\overrightarrow{B'A'}\)是\(\underline{\quad \quad}\)向量.

7在空间四边形\(ABCD\)中, \(2 \overrightarrow{A B}+\overrightarrow{C A}+\overrightarrow{B C}-\overrightarrow{A D}+\overrightarrow{B D}=\)\(\underline{\quad \quad}\).
8 已知 \(A,B,C\)三点不共线,对平面\(ABC\)外一点\(O\),给出下列表达式: \(2 \overrightarrow{O M}=x \overrightarrow{O A}+y \overrightarrow{O B}+\dfrac{1}{3} \overrightarrow{O C}\),其中\(x,y\)是实数,若点\(M\)与 \(A,B,C\)四点共面,则\(x+y=\)\(\underline{\quad \quad}\).
9已知非零向量\(\vec{a}\),\(\vec{b}\)不共线.若 \(\overrightarrow{A B}=\vec{a}+\vec{b}\), \(\overrightarrow{A C}=2 \vec{a}+8 \vec{b}\), \(\overrightarrow{A D}=3 \vec{a}-3 \vec{b}\),
求证:\(A,B,C,D\)四点共面.
10如图所示,在长方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(M\)为\(DD_1\)的中点,\(N∈AC\),且\(AN:NC=2\),求证:\(A_1,B,N,M\)四点共面.

参考答案
-
答案 \(A\)
解析 \(\overrightarrow{AB}\)与\(\overrightarrow{BA}\)互为相反向量,模相等,故\(A\)正确;\(B\)中所有单位向量的终点构成球面而不是圆,故\(B\)错误;
有向线段只是空间向量的一种表示形式,二者并不相同,故\(C\)错误;
不相等的向量可以长度相等而方向不同,故\(D\)错误. -
答案 \(C\)
解析 对于\(A\),空间向量的平行具有传递性,但前提是\(\vec{b}≠\vec{0}\),故\(A\)错;
对于\(B\),向量\(\vec{a},\vec{b},\vec{c}\)所在的直线可以互为异面直线,故\(B\)错;
对于\(D\),要成立的前提是\(\vec{b}≠\vec{0}\). -
答案 \(C\)
解析 在\(C\)选项中, \(\overrightarrow{A B}+\overrightarrow{A_{1} D_{1}}+\overrightarrow{C_{1} A_{1}}=(\overrightarrow{A B}+\overrightarrow{A D})+\overrightarrow{C A}=\overrightarrow{A C}+\overrightarrow{C A}=\overrightarrow{0}\). -
答案 \(A\)
解析 空间中任何两个向量都是共面向量,但不一定共线. -
答案 \(B\)
解析 连接\(ON\),
\(∵N\)是\(BC\)的中点, \(\therefore \overrightarrow{O N}=\dfrac{1}{2} \overrightarrow{O B}+\dfrac{1}{2} \overrightarrow{O C}\),
\(\because \overrightarrow{O M}=2 \overrightarrow{M A}\), \(\therefore \overrightarrow{O M}=\dfrac{2}{3} \overrightarrow{O A}\),
\(\therefore \overrightarrow{M N}=\overrightarrow{O N}-\overrightarrow{O M}=\dfrac{1}{2} \overrightarrow{O B}+\dfrac{1}{2} \overrightarrow{O C}-\dfrac{2}{3} \overrightarrow{O A}=-\dfrac{2}{3} \vec{a}+\dfrac{1}{2} \vec{b}+\dfrac{1}{2} \vec{c}\),
故选:\(B\).

-
答案 相等 相反
-
答案 \(\vec{0}\)
解析 \(2 \overrightarrow{A B}+\overrightarrow{C A}+\overrightarrow{B C}-\overrightarrow{A D}+\overrightarrow{B D}=2 \overrightarrow{A B}+(\overrightarrow{B C}+\overrightarrow{C A})+(\overrightarrow{D A}+\overrightarrow{B D})\)
\(=2 \overrightarrow{A B}+\overrightarrow{B A}+\overrightarrow{B A}=2 \overrightarrow{A B}+2 \overrightarrow{B A}=\overrightarrow{0}\). -
答案 \(\dfrac{5}{3}\)
解析 \(\because 2 \overrightarrow{O M}=x \overrightarrow{O A}+y \overrightarrow{O B}+\dfrac{1}{3} \overrightarrow{O C}\), \(\therefore \overrightarrow{O M}=\dfrac{1}{2} x \overrightarrow{O A}+\dfrac{1}{2} y \overrightarrow{O B}+\dfrac{1}{6} \overrightarrow{O C}\),
\(∵\)点\(M,A,B,C\)四点共面,
\(\therefore \dfrac{1}{2} x+\dfrac{1}{2} y+\dfrac{1}{6}=1\), \(\therefore x+y=\dfrac{5}{3}\). -
证明 \(∵\)不存在实数\(k\),使得 \(\overrightarrow{A D}=k \overrightarrow{A B}\),可知 \(\overrightarrow{A D}, \overrightarrow{A B}\)不共面.
令 \(\overrightarrow{A C}=x \overrightarrow{A B}+y \overrightarrow{A D}\),
则 \(2 \vec{a}+8 \vec{b}=x(\vec{a}+\vec{b})+y(3 \vec{a}-3 \vec{b})=(x+3 y) \vec{a}+(x-3 y) \vec{b}\),
又非零向量\(\vec{a}\),\(\vec{b}\)不共线,
\(\therefore\left\{\begin{array}{l} 2=x+3 y \\ 8=x-3 y \end{array}\right.\) ,解得\(x=5,y=-1\).
\(∴\)存在实数\(x,y\)使得 \(\overrightarrow{A C}=x \overrightarrow{A B}+y \overrightarrow{A D}\),
\(∴A,B,C,D\)四点共面. -
证明 设 \(\overrightarrow{A A_{1}}=\vec{a}, \overrightarrow{A B}=\vec{b}, \overrightarrow{A D}=\vec{c}\),则 \(\overrightarrow{A_{1} B}=\vec{b}-\vec{a}\),
\(∵M\)为\(DD_1\)的中点, \(\therefore \overrightarrow{A_{1} M}=\vec{C}-\dfrac{1}{2} \vec{a}\),
又\(∵AN:NC=2\), \(\therefore \overrightarrow{A N}=\dfrac{2}{3} \overrightarrow{A C}=\dfrac{2}{3}(\vec{b}+\vec{C})\),
\(\therefore \overrightarrow{A_{1} N}=\overrightarrow{A N}-\overrightarrow{A A_{1}}=\dfrac{2}{3}(\vec{b}+\vec{c})-\vec{a}\)\(=\dfrac{2}{3}(\vec{b}-\vec{a})+\dfrac{2}{3}\left(\vec{c}-\dfrac{1}{2} \vec{a}\right)=\dfrac{2}{3} \overrightarrow{A_{1} B}+\dfrac{2}{3} \overrightarrow{A_{1} M}\),
\(\therefore \overrightarrow{A_{1} N}, \overrightarrow{A_{1} B}, \overrightarrow{A_{1} M}\)为共面向量,
又三向量有相同的起点\(A_1\),\(∴A_1,B,N,M\)四点共面.
【B组---提高题】
1.给出下列命题:
①若\(A,B,C,D\)是空间任意四点,则有 \(\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C D}+\overrightarrow{D A}=\overrightarrow{0}\);
② \(|\vec{a}|-|\vec{b}|=|\vec{a}+\vec{b}|\)是 \(\vec{a}, \vec{b}\)共线的充要条件;
③若 \(\overrightarrow{A B}, \overrightarrow{C D}\)共线,则 \(\overrightarrow{A B} / / \overrightarrow{C D}\);
④对空间任意一点\(O\)与不共线的三点\(A,B,C\),若 \(\overrightarrow{O P}=x \overrightarrow{O A}+y \overrightarrow{O B}+z \overrightarrow{O C}\)(其中\(x,y,z∈R\)),则\(P,A,B,C\)四点共面.
其中假命题的个数是 ( )
A.\(1\) \(\qquad \qquad\) B.\(2\) \(\qquad \qquad\) C.\(3\) \(\qquad \qquad\) D.\(4\)
2.已知矩形\(ABCD\),\(P\)为平面\(ABCD\)外一点,且\(PA⊥\)平面\(ABCD\),\(M\),\(N\)分别为\(PC,PD\)上的点,且 \(\overrightarrow{N M}=x \overrightarrow{A B}+y \overrightarrow{A D}+z \overrightarrow{A P}\), \(\overrightarrow{P M}=2 \overrightarrow{M C}\), \(\overrightarrow{P N}=\overrightarrow{N D}\),则\(x+y+z\)的值为( )

A. \(-\dfrac{2}{3}\) \(\qquad \qquad\) B. \(\dfrac{2}{3}\) \(\qquad \qquad\) C.\(1\) \(\qquad \qquad\) D. \(\dfrac{5}{6}\)
3.已知在正方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(P,M\)为空间任意两点,如果有 \(\overrightarrow{P M}=\overrightarrow{P B_{1}}+7 \overrightarrow{B A}+6 \overrightarrow{A A_{1}}-4 \overrightarrow{A_{1} D_{1}}\),那么点\(M\)必( )
A.在平面\(BAD_1\)内 \(\qquad \qquad\) B.在平面\(BA_1 D\)内 \(\qquad \qquad\) C.在平面\(BA_1 D_1\)内 \(\qquad \qquad\) D.在平面\(AB_1 C_1\)内
4.在棱长为\(1\)的正方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(E\),\(F\),\(G\)分别在棱\(BB_1\),\(BC\),\(BA\)上,且满足\(\overrightarrow{B E}=\dfrac{3}{4} \overrightarrow{B B_{1}}\), \(\overrightarrow{B F}=\dfrac{1}{2} \overrightarrow{B C}\), \(\overrightarrow{B G}=\dfrac{1}{2} \overrightarrow{B A}\),\(O\)是平面\(B_1 GF\),平面\(ACE\)与平面\(B_1 BDD_1\)的一个公共点,设 \(\overrightarrow{B O}=x \overrightarrow{B G}+y \overrightarrow{B F}+z \overrightarrow{B E}\),则\(x+y+z=\)( )
A. \(\dfrac{4}{5}\) \(\qquad \qquad\) B.\(\dfrac{6}{5}\) \(\qquad \qquad\) C. \(\dfrac{7}{5}\) \(\qquad \qquad\) D. \(\dfrac{8}{5}\)
5在空间四边形\(ABCD\)中,连结\(AC\),\(BD\).若\(△BCD\)是正三角形,且\(E\)为其中心,则 \(\overrightarrow{A B}+\dfrac{1}{2} \overrightarrow{B C}-\dfrac{3}{2} \overrightarrow{D E}-\overrightarrow{A D}\)的化简结果为\(\underline{\quad \quad}\).
参考答案
-
答案 \(C\)
解析 ①若\(A,B,C,D\)是空间任意四点,则有 \(\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C D}+\overrightarrow{D A}=\overrightarrow{0}\);真命题.
② \(\|\vec{a}|-| \vec{b}\|=|\vec{a}+\vec{b}|\)或 \(|\vec{a}|+|\vec{b}|=|\vec{a}+\vec{b}|\)是 \(\vec{a}, \vec{b}\)共线的充要条件;假命题.
③若 \(\overrightarrow{A B}, \overrightarrow{C D}\)共线,则 \(\overrightarrow{A B} / / \overrightarrow{C D}\);也可能重合,假命题.
④对空间任意一点\(O\)与不共线的三点\(A,B,C\),若 \(\overrightarrow{O P}=x \overrightarrow{O A}+y \overrightarrow{O B}+z \overrightarrow{O C}\)(其中\(x,y,z∈R\)),
当且仅当\(x+y+z=1\)时,则\(P,A,B,C\)四点共面.假命题.
故选:\(C\). -
答案 \(B\)
解析 由题可知 \(\Rightarrow \overrightarrow{P C}=\overrightarrow{A B}+\overrightarrow{B C}-\overrightarrow{A P}=\overrightarrow{A B}+\overrightarrow{A D}-\overrightarrow{A P}, \overrightarrow{D P}=\overrightarrow{A P}-\overrightarrow{A D}\),
所以 \(\overrightarrow{N M}=\overrightarrow{N P}+\overrightarrow{P M}=\dfrac{1}{2} \overrightarrow{D P}+\dfrac{2}{3} \overrightarrow{P C}=\dfrac{1}{2}(\overrightarrow{A P}-\overrightarrow{A D})+\dfrac{2}{3}(\overrightarrow{A B}+\overrightarrow{A D}-\overrightarrow{A P})\)
\(=-\dfrac{1}{6} \overrightarrow{A P}+\dfrac{2}{3} \overrightarrow{A B}+\dfrac{1}{6} \overrightarrow{A D}\),
所以 \(x=\dfrac{2}{3}, y=\dfrac{1}{6}, z=-\dfrac{1}{6}\),所以 \(x+y+z=\dfrac{2}{3}\),
故选:\(B\). -
答案 \(C\)
解析 因为 \(\overrightarrow{P M}=\overrightarrow{P B_{1}}+7 \overrightarrow{B A}+6 \overrightarrow{A A_{1}}-4 \overrightarrow{A_{1} D_{1}}=\overrightarrow{P B_{1}}+\overrightarrow{B A}+6 \overrightarrow{B A_{1}}-4 \overrightarrow{A_{1} D_{1}}\)
\(=\overrightarrow{P B_{1}}+\overrightarrow{B_{1} A_{1}}+6 \overrightarrow{B A_{1}}-4 \overrightarrow{A_{1} D_{1}}=\overrightarrow{P A_{1}}+6\left(\overrightarrow{P A_{1}}-\overrightarrow{P B}\right)-4\left(\overrightarrow{P D_{1}}-\overrightarrow{P A_{1}}\right)\)
\(=11 \overrightarrow{P A_{1}}-6 \overrightarrow{P B}-4 \overrightarrow{P D_{1}}\),
所以\(M,B,A_1,D_1\)四点共面,即点\(M\)必在平面\(BA_1 D_1\)内.
故选:\(C\). -
答案 \(B\)
解析 正方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(\overrightarrow{B E}=\dfrac{3}{4} \overrightarrow{B B_{1}}\), \(\overrightarrow{B F}=\dfrac{1}{2} \overrightarrow{B C}\), \(\overrightarrow{B G}=\dfrac{1}{2} \overrightarrow{B A}\),
\(\overrightarrow{B O}=x \overrightarrow{B G}+y \overrightarrow{B F}+z \overrightarrow{B E}=\dfrac{1}{2} x \overrightarrow{B A}+\dfrac{1}{2} y \overrightarrow{B C}+z \overrightarrow{B E}=x \overrightarrow{B G}+y \overrightarrow{B F}+\dfrac{3}{4} z \overrightarrow{B B_{1}},\),
\(∵O,A,C,E\)四点共面,\(O,D,E,B_1\)四点共面,
\(\therefore\left\{\begin{array}{l} \dfrac{1}{2} x+\dfrac{1}{2} y+z=1 \\ x+y+\dfrac{3}{4} z=1 \end{array}\right.\),解得 \(x+y=\dfrac{2}{5}, \quad z=\dfrac{4}{5}\);
\(\therefore x+y+z=\dfrac{6}{5}\).
故选:\(B\). -
答案 \(\vec{0}\)
解析 如图,延长\(DE\)交\(BC\)于点\(F\),根据题意知\(F\)为\(BC\)的中点.

又因为\(E\)为正三角形\(BCD\)的中心,
所以 \(\overrightarrow{D E}=\dfrac{2}{3} \overrightarrow{D F}\),即 \(\overrightarrow{D F}=\dfrac{3}{2} \overrightarrow{D E}\),
所以 \(\overrightarrow{A B}+\dfrac{1}{2} \overrightarrow{B C}-\dfrac{3}{2} \overrightarrow{D E}-\overrightarrow{A D}=(\overrightarrow{A B}-\overrightarrow{A D})+\overrightarrow{B F}-\dfrac{3}{2} \overrightarrow{D E}\)\(=\overrightarrow{D B}+\overrightarrow{B F}-\overrightarrow{D F}=\overrightarrow{D F}-\overrightarrow{D F}=\overrightarrow{0}\).
【C组---拓展题】
1.在三棱锥\(A-BCD\)中,\(P\)为\(△BCD\)内一点,若 \(S_{\triangle P B C}=1\),\(S_{\triangle P C D}=2\), \(S_{\triangle P B D}=3\),则 \(\overrightarrow{A P}=\) ( )
A.\(\dfrac{1}{3} \overrightarrow{A B}+\dfrac{1}{6} \overrightarrow{A C}+\dfrac{1}{2} \overrightarrow{A D}\) \(\qquad \qquad\) B. \(\dfrac{1}{2} \overrightarrow{A B}+\dfrac{1}{6} \overrightarrow{A C}+\dfrac{1}{3} \overrightarrow{A D}\)
C. \(\dfrac{1}{3} \overrightarrow{A B}+\dfrac{1}{2} \overrightarrow{A C}+\dfrac{1}{6} \overrightarrow{A D}\) \(\qquad \qquad\) D. \(\dfrac{1}{6} \overrightarrow{A B}+\dfrac{1}{3} \overrightarrow{A C}+\dfrac{1}{2} \overrightarrow{A D}\)
2.如图所示,已知四边形\(ABCD\)是平行四边形,\(P\)点是四边形\(ABCD\)所在平面外一点,连接\(PA\)、\(PB\)、\(PC\)、\(PD\),设点\(E,F,G,H\)分别为\(△PAB\)、\(△PBC\)、\(△PCD\)、\(△PDA\)的重心.试用向量法证明\(E,F,G,H\)四点共面.

参考答案
-
答案 \(C\)
解析 三棱锥\(A-BCD\)中,\(P\)为\(△BCD\)内一点,如图所示:
延长\(PB\)至\(B_1\),使得\(PB_1=2PB\),延长\(PC\)至\(C_1\),使得\(PC_1=3PC\),连接\(DB_1,B_1 C_1,C_1 D\),
因为 \(S_{\triangle P B C}=1\),\(S_{\triangle P C D}=2\), \(S_{\triangle P B D}=3\),
所以 \(S_{\triangle P B_{1} C_{1}}=S_{\triangle P C_{1} D}=S_{\triangle P B_{1} D}\),
所以\(P\)为\(△B_1 C_1 D\)的重心,所以 \(\overrightarrow{P D}+\overrightarrow{P B_{1}}+\overrightarrow{P C_{1}}=\overrightarrow{0}\),
即 \(P D+2 \overrightarrow{P B}+3 \overrightarrow{P C}=\overrightarrow{0}\),
所以 \((\overrightarrow{A D}-\overrightarrow{A P})+2(\overrightarrow{A B}-\overrightarrow{A P})+3(\overrightarrow{A C}-\overrightarrow{A P})=\overrightarrow{0}\),
所以 \(\overrightarrow{A P}=\dfrac{1}{3} \overrightarrow{A B}+\dfrac{1}{2} \overrightarrow{A C}+\dfrac{1}{6} \overrightarrow{A D}\).
故选:\(C\).

-
证明 分别延长\(PE,PF,PG,PH\),交对边于\(M,N,Q,R\)点,
因为\(E,F,G,H\)分别是所在三角形的重心,
所以\(M,N,Q,R\)为所在边的中点,
顺次连接\(M,N,Q,R\)得到的四边形为平行四边形,
且有 \(\overrightarrow{P E}=\dfrac{2}{3} \overrightarrow{P M}\), \(\overrightarrow{P F}=\dfrac{2}{3} \overrightarrow{P N}\), \(\overrightarrow{P G}=\dfrac{2}{3} \overrightarrow{P Q}\), \(\overrightarrow{P H}=\dfrac{2}{3} \overrightarrow{P R}\);如图所示,

\(\therefore \overrightarrow{M Q}=\overrightarrow{M N}+\overrightarrow{M R}=(\overrightarrow{P N}-\overrightarrow{P M})+(\overrightarrow{P R}-\overrightarrow{P M})\)
\(=\dfrac{3}{2}(\overrightarrow{P F}-\overrightarrow{P E})+\dfrac{3}{2}(\overrightarrow{P H}-\overrightarrow{P E})=\dfrac{3}{2}(\overrightarrow{E F}+\overrightarrow{E H})\);
又 \(\because \overrightarrow{M Q}=\overrightarrow{P Q}-\overrightarrow{P M}=\dfrac{3}{2} \overrightarrow{P G}-\dfrac{3}{2} \overrightarrow{P E}=\dfrac{3}{2} \overrightarrow{E G}\),
\(\therefore \dfrac{3}{2} \overrightarrow{E G}=\dfrac{3}{2}(\overrightarrow{E F}+\overrightarrow{E H})\), \(\therefore \overrightarrow{E G}=\overrightarrow{E F}+\overrightarrow{E H}\)
由共面向量定理知:\(E,F,G,H\)四点共面.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号