杂题选解
Tag
- 结论(包括定理,指的是通过题目信息或者用到的知识点推出一个性质的题目、脑洞题)
- 二分
- 暴力
- 优化
- 矩阵乘法
- 贪心(贪心题或者题目中用到贪心)
- 反悔贪心
- 位运算(下分具体运算)
- 搜索
- 多源BFS
- Flood fill
- 数据结构
- 线段树
- 字符串
- AC自动机
- 数论
- 快速幂
- 技巧(做题通用的小trick)
- 构造
- 计算几何
- 点到线段的距离
- 扫描线
- 模拟
- 图形模拟
- 字符串(指的是问题载体是字符串的题目)
- 图论
- 最短路
- dijkstra
- 最小生成树
- 超级源点
- 拓扑排序
- 反向遍历
- 点分治
- 树上倍增
- 最短路
- 动态规划
- 分组背包
- 数位DP
- 图上DP
- 状压DP
- 状态机DP
- 区间DP
- 网络流
- 最小费用最大流
薄弱的知识点
- DP
- 状压DP
- 状态机DP
- 区间DP
- 网络流(建图)
- 最小费用最大流
- 线段树
- 点分治
- 树上倍增
- 强连通分量
- AC自动机
模拟
模拟的关键在于想好怎么存储
L-shapes
模拟、图形模拟
L-shapes - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
题解较复杂Codeforces Round #817 (Div. 4) Editorial - Codeforces
代码实现比较难,要多写几遍
Submission #205513970 - Codeforces
矩阵旋转
图形模拟
对于n阶矩阵,行号和列号从0~2^n-1,用二进制表示发现,如果横纵坐标的最高位都为0,则在n阶矩阵的左上区域,其他同理。
所以,对于n阶矩阵中位置为(x, y)的点:
- 首先由最高位求出它在n阶矩阵的哪个区域
- 观察可以发现剩余位是它在n-1阶矩阵中的位置。也就是说当n-1阶矩阵没有旋转时,n阶矩阵中(x, y)的符号和n-1阶矩阵中(tx, ty)的符号相同。如果旋转了,则已旋转的n-1阶矩阵中(tx, ty)的符号应该是原n-1阶矩阵中(tx', ty')的符号+k (k = 1, 2, 3)。
- 通过以上分析,结合递归函数的定义,它返回的是未旋转的n阶矩阵中(x, y)位置的值,如果是已知旋转后矩阵的x,y,则要反推出原矩阵的x,y作为函数的参数。且元素旋转后自身也要变,顺时针旋转90度在mark数组中的下标就对应+1。
- 递归出口是0阶矩阵时,返回的是0,表示它是mark矩阵中下标为0的元素
>。
技巧:图像旋转问题,只要算出90度,180,270只需做2,3次90即可。
一种方便的做法是创建一个备份数组,在原数组中用坐标变换公式算出每一个(x, y)是谁转过来的。
坐标变换公式的推导要抓住:同一列的元素旋转之后一定在同一行,同一行的元素旋转之后一定在同一列。
关于矩阵旋转的相关题目:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
char mark[] = ">v<^";
int calc(int x, int y, int n) // 返回在n阶矩阵中(x, y)这个位置的符号在mark数组中的下标
{
int dx = x >> (n - 1) & 1, dy = y >> (n - 1) & 1; //
int m = 1 << (n - 1);
int tx = x & (m - 1), ty = y & (m - 1);
if (n == 0) return 0;
if (dx == 0 && dy == 0) return calc(tx, ty, n - 1);
else if (dx == 1 && dy == 0) return calc(m - 1 - ty, tx, n - 1) + 1;
else if (dx == 0 && dy == 1) return calc(m - 1 - tx, m - 1 - ty, n - 1) + 2;
else if (dx == 1 && dy == 1) return calc(ty, m - 1 - tx, n - 1) + 3;
}
int main()
{
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
int n;
cin >> n;
for (int i = 0; i < (1 << n); i ++ , cout << "\n")
for (int j = 0; j < (1 << n); j ++ )
cout << mark[calc(i, j, n) % 4];
return 0;
}
Water Level
模拟、贪心、技巧
Water Level - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
题目大意
有一个水桶,水桶里面有k升水,我们每天开始的时候可以往里面注入y升水,每天的消耗量是x升,问我们能否使水量在[l,r]范围内保持t天
解析
一个技巧:每轮减小\(x\),由\(r\)减小到\(l\)需要\((r - l) / x\)轮 [下取整,算的是间隔数而不是点数]
分类讨论
- x > y
- 说明水量会单调递减,则最多坚持\((k - l) / (x - y)\)天
- 特判:如果第一天加水会超过r,则第一天不加,因为只要减少一次x后,加水就不会溢出了
- x <= y
- 目的是让水位保持在[l, r]之间,所以最好的方法是当水位要小于\(l\)时才加水,这是因为\(y > x\),只要加水就一定不会减到低于\(l\)了,而且只在必要时加水也能减少溢出的概率(贪心)
- 所以我们的做法是:先将水减到不能再减,判断此时的剩余天数。
- 天数<=0,说明成功维持了\(t\)天
- 否则,在接下来的一天:加水,判断是否溢出、减水
- 一个优化:当剩余水量出现循环时,说明从上一次到达这个水位开始都能维持住,那接下来同样也是循环,一定能维持住
- 判断循环:\(k1 \% x == k2 \% x\)。k1 = k2时,显然;k1 != k2,由于两者之间差x的整数倍,只需要再减这么多天的水即可相等,所以也认为是出现了循环。
AC代码:Submission #205511487 - Codeforces
命令行选项
技巧、stringstream
Z字形扫描
路径解析
技巧、模拟
下标遍历string时,不要用s[i],因为之前输入的会保留,要用s.size(),总之,用s[i]不一定能防止越界
#define LOCAL
#ifdef LOCAL
#define dbg(...) fprintf(stderr, __VA_ARGS__)
#else
#define dbg(...)
#define NDEBUG
#endif
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
vector<string> get(string &s)
{
vector<string> res;
for (int i = 0; i < s.size(); i ++ ) // 下标遍历string时,不要用s[i],因为之前输入的会保留,要用s.size(),总之,用s[i]不一定能防止越界
{
if (s[i] == '/') continue;
int j = i + 1;
while (j < s.size() && s[j] != '/') j ++ ;
res.push_back(s.substr(i, j - i));
i = j;
}
return res;
}
void work(vector<string> cur, vector<string> s)
{
for (int i = 0; i < s.size(); i ++ )
{
if (s[i] == ".") continue;
else if (s[i] == "..")
{
if (cur.empty()) continue;
else cur.pop_back();
}
else cur.push_back(s[i]);
}
if (cur.empty()) cout << "/" << "\n";
else
{
for (auto i : cur)
cout << "/" << i;
cout << "\n";
}
}
int main()
{
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
int n;
string str;
cin >> n >> str;
vector<string> cur = get(str), ap;
cin.get();
string x;
while (n -- )
{
getline(cin, x);
auto path = get(x);
if (x.size() && x[0] == '/') work(ap, path);
else work(cur, path);
}
return 0;
}
炉石传说
用类结构体来做模拟
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
struct Slave
{
int health, atk;
bool die;
Slave(int _h, int _a): health(_h), atk(_a), die(false) {}
Slave(): health(), atk(), die(false) {}
void defend(Slave & attacker)
{
health -= attacker.atk;
if (health <= 0) die = true;
}
void attack(Slave & defender)
{
health -= defender.atk;
if (health <= 0) die = true;
}
};
struct Hero
{
int health, atk;
bool win;
vector<Slave> slaves;
Hero(): health(30), atk(0), win(false) {}
void summon(int pos, int h, int a)
{
Slave add(h, a);
slaves.insert(slaves.begin() + pos - 1, add);
}
void defend(Hero & oppo, int atkpos, int atkedpos)
{
atkedpos -- , atkpos -- ;
Slave & attacker = oppo.slaves[atkpos];
if (atkedpos == -1)
{
health -= attacker.atk;
die(oppo);
}
else
{
Slave & defender = slaves[atkedpos];
defender.defend(attacker);
attacker.attack(defender);
if (defender.die) slaves.erase(slaves.begin() + atkedpos);
if (attacker.die) oppo.slaves.erase(oppo.slaves.begin() + atkpos);
}
}
void die(Hero & oppo)
{
if (health > 0) return;
else
{
win = false;
oppo.win = true;
}
}
};
int main()
{
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
int n;
cin >> n;
Hero heros[2];
int turn = 0;
while (n -- )
{
string op;
cin >> op;
if (op == "end")
{
turn = !turn;
continue;
}
Hero & actor = heros[turn];
if (op == "summon")
{
int pos, a, h;
cin >> pos >> a >> h;
actor.summon(pos, h, a);
}
else
{
int attacker, defender;
cin >> attacker >> defender;
heros[!turn].defend(actor, attacker, defender); // actor攻击,另一个防守
}
}
if (heros[0].win) cout << 1 << "\n";
else if (heros[1].win) cout << -1 << "\n";
else cout << 0 << "\n";
for (int i = 0; i < 2; i ++ )
{
cout << heros[i].health << "\n";
cout << heros[i].slaves.size() << ' ';
for (auto s : heros[i].slaves) cout << s.health << ' ';
cout << "\n";
}
return 0;
}
权限查询
模拟、map的嵌套使用
auto & t = users[str][item.first]; // 两层不存在,也能返回一个0,map牛逼!
t = max(t, item.second);
梯度求解
定义一个类来存储多项式
- 多项式中的每一项是一个长度为n+1的vector,第0位是这一项的系数,第1~n项是第i个自变量的次数,则多项式就是vector的vector。
- 多项式乘法:两个多项式的每一项分别相乘,两个项相乘的规则是:系数相乘,对应自变量的次数相加。
- 多项式加法:直接把两个多项式的项存到一个多项式里。
- 多项式减法:在存储中,各项之间是加法。则减法就是作为减数的多项式的每一项系数变成相反数。然后做加法。
- 多项式求偏导,每一项只有一个是自变量,其他的是常数,那求导的过程就是自变量次数减1,系数=系数*次数
- 多项式求值:遍历每一项,系数为0则跳过,不为0时用快速幂求每一个乘方,项内相乘,各项的乘积相加
解压缩
如果将一个字节(2个字符)的字符串化为整型,那一些操作就可以用除法和取模来解决
假设a是一个字节化为整型的结果
- 取高六位:a / 4
- 取2到4位:a % 32 / 4
- 取高3位:a / 32
- 取低2位:a % 4
- 高3位和后1个字节拼接:a / 32 * 256 + 后1个字节对应的整数
把所有的输出都先存在output中,当前解压缩的字节数=output.size() / 2(一个字节两个字符)
偏移量为offset的字节的起始下标是offset * 2
DHAP
这份代码官网评测的最好结果是5.703s 56.67MB,unordered_map确实比map快不少,至少2s吧
没有用bitset,我的做法是建立一棵二叉树
- 读入表达式,递归建树,叶子结点就是BASE_EXPR,非叶子结点就存是
&还是| - 从根节点开始递归判定,如果是叶子结点,单独写了一个函数来判断这个用户是否满足该叶子节点存的BASE_EXPR,如果是非叶子节点,返回左右子树的结果的与运算或者是或运算的结果
注意函数中的idx都是引用,每个函数都会修改idx的。
双指针
盛最多水的容器
双指针,技巧

观察性质:任取两根柱子a,b,假设a<b。对于a,任意一根a,b之间的柱子都不能与它构成更大的容器。
证明:设中间的柱子为c
- c>a,由于容器高度取决于短的柱子,因此高度不变,而宽度减小
- c<a,不仅高度减小,宽度也减小
因此,在下一根柱子只能选择a,b之间的柱子的条件下,要想得到更大的容器,只能短的柱子向中间选择。
基于这个性质,我们的选择策略如下:
两根柱子分别初始化为最左和最右的两个柱子i,j,每次都朝着可能变大的方向走
- 短的柱子向中间选择
- 两根柱子高度相同时任意移动一根
直到i>=j为止。由于我们每次都朝着可能变大的方向走,一定经过了容器最大的状态,因此在过程中不断取max即可。
接雨水
双指针,技巧

考察坐标为x的柱子处的水
- 宽度:就是柱子的宽度1
- 水位:如果x处有水,它一定处在一个“洼地”里,“洼地”的左右边界为x左边和右边的最高柱子lmax和rmax,“洼地”的水位H为min(lmax, rmax),洼地在x处的实际水位为H-height[x]。
基于以上分析,我们只需要求出每个柱子左边和右边最高的柱子,然后用式子算出该位置的水位(可能大于0,小于0,或者等于0),如果水位大于0,则累加到答案
实现方法:
-
这里左右指针分别是当前前后缀的最大值,如果左边的最高柱子比较矮,那对于左指针右边的那根柱子来说,min(lmax, rmax)就是当前的lmax,因此这个柱子的水位就可以算出来了。
之后将左指针右移一个,继续比较。右指针同理。
-
其实只要先和当前的柱子x取max,就不需要判断H-height[x]的正负了,这样写起来更简单
滑动窗口
找到字符串中所有字母异位词
技巧
https://leetcode.cn/problems/find-all-anagrams-in-a-string
这道题值得关注的是官方题解里的优化方法
问题:如何判断两个数组是否相同,设数组长度为n,数组会被修改,要判断的次数为m
-
朴素方法:遍历两个数组,逐个比较,时间复杂度O(n * m),当数组很长时不适用
-
优化方法:维护一个变量differ,首先遍历一次,记录初始时两个数组不同的元素的个数。
每次修改时,如果对应元素从不同变成相同,differ--,反之differ++。
当differ==0时,两个数组相等,否则不相等。
如果能在O(1)的时间内完成对differ的更新,则时间复杂度为O(n+m)。
二分
Scuza
二分
Scuza - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
要点:
- 二分要注意上溢和下溢,可以设在两边设哨兵或者错位存储下标对应的答案。
- 要在数列a中找到从左数第一个大于k的数的位置:构造数列m,m[i] = max(a[1 ~ i]),也就是a数列的前n项最大值数列,然后在m中二分找到第一个大于k的数即可。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
void solve()
{
vector<ll> pref; // 前缀和数组
pref.push_back(0);
vector<int> prefmax; // 前n项最大值数组
prefmax.push_back(0); // 设置下溢的哨兵
int n, q;
cin >> n >> q;
for (int i = 0; i < n; i ++ )
{
int x;
cin >> x;
pref.push_back(pref.back() + x);
prefmax.push_back(max(prefmax.back(), x));
}
while (q -- )
{
int k;
cin >> k;
int ind = upper_bound(prefmax.begin(), prefmax.end(), k) - prefmax.begin();
cout << pref[ind - 1] << " ";
}
cout << endl;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
int n;
cin >> n;
while (n -- )
solve();
}
贪心
Warehouse Store
贪心、反悔贪心
【蒟蒻算法】反悔贪心 - 蒟蒻のBLOG (jvruo.com)
【P3545 POI2012】HUR-Warehouse Store - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
反悔贪心法
-
反悔堆(用堆来存储当前所有选择的任务)
-
用时一定模型
-
问题描述
我们考虑这样一个问题,我们有n个任务(n≤1e5),每个任务都恰好需要一个单位时间完成,并且每个任务都有两个属性——截止日期和价值。在截止日期前完成任务就可以得到这个任务产生的价值。每个单位时间我们都可以选择这n个任务当中还没有做过的并且还没有截止的任务中的一个去完成,问我们最后最多能得到多少价值呢?
-
贪心思路
价值高的任务和价值低的任务完成耗时相同,令总价值最大。我们可以按截止日期从早到晚排序。如果一个任务
- 能在DDL前完成,暂时完成它
- 已经超过了截止日期。那么我们找到目前所有被暂时完成的任务中,价值最小的那个(即堆顶元素)。但如果堆顶任务的价值小于我们当前考虑任务的价值,这就是代表着我们已选任务的价值最小值是不及我们当前考虑的这个任务的,那我们就不做堆顶的任务,用做之前那个任务的时间去做我们当前考虑的这个任务就可以啦。
-
例题
-
-
价值一定模型
-
问题描述
我们有n个任务(n≤1e5),并且每个任务都有两个属性——截止日期和完成耗时。在截止日期前完成任务就可以得到这个任务产生的价值。在同一时间我们只能去做一个任务。所有任务的价值都是一样的,问我们最后最多能完成多少个任务。
-
贪心思路
耗时长和耗时短的任务价值相同,要完成最多的任务。我们还是按截止日期从早到晚排序。如果一个任务
- 能在DDL前完成,暂时完成它
- 已经超过了截止日期。那么我们找到目前所有被暂时完成的任务中,耗时最长的那个(即堆顶元素)。但如果堆顶任务的耗时大于我们当前考虑任务的耗时,这就是代表着我们已选任务的耗时最大值是大于我们当前考虑的这个任务的,那我们就不做堆顶的任务,用做之前那个任务的时间去做我们当前考虑的这个任务就可以啦,还能剩下一些时间,显然更优。
-
例题
-
-
-
反悔自动机(没学)
解析(from hkk)
首先给定我们这个题目的贪心方法:
我们依次扫描所有的订单,先尽可能地满足我们已经遇到的所有订单,并维护当前的库存容量,我们记作 \(V\)。
对于第 \(i\) 个订单,如果 \(V \geq b_i\),那么就是说这个订单可以被直接满足,那么我们就暂时通过这个订单,并更新库存等信息。
如果 \(V < b_i\),即这个订单不可以被直接满足。那么我们找到目前所有被暂时通过的订单中,\(b\) 值最大的那一个,假设为第 \(j\) 个订单。如果 \(b_j > b_i\),那么我们将第 \(j\) 个订单退掉,将第 \(i\) 个订单暂时标记为通过;否则,解除第 \(i\) 个订单。
我们可以用一个大根堆(优先队列)来维护所有被暂时通过的订单,那么可以在 \(O(n\log n)\) 的时间复杂度完成这个算法。
下面我们理解一下这个贪心的正确性。
这种贪心和我们常见的贪心有些不一样。
这一类的贪心并不满足常规的“最优子结构”的性质,这一种问题并不一定能保证,整体最优解的一个子集一定是局部的最优解。
(这种贪心民间一般称为反悔贪心法。)
简单而不严谨的理解方法:我们将一个订单暂时通过,即使它不是最优的,我们也可以在保持贡献不变的情况下将它替换掉。而在替换的时候,我们只要保持在答案最优的情况下,我们的库存量尽量多,只要库存越多后面的答案就可能越好。
我们考虑使用归纳的方法来证明这一算法:
首先我们定义一个解比另一个解“优”:对于同一个子问题的两个解 \(S, T\),如果 \(|S| > |T|\),或 \(|S| = |T|\) 且 \(\sum_{i \in S} b_i < \sum_{i \in T} b_i\),那么我们称 \(S\) 优于 \(T\)。
即,已知集合 \(S_{i-1}\) 是前 \(i-1\) 天的最优解集合,证明通过我们的贪心算法得到的新集合 \(S_i\) 是前 \(i\) 天的最优解集合。
根据定义,\(V = \sum_{j=1}^{i} a_j - \sum_{j\in S_{i-1}} b_j\)。我们记 \(V_{S_i} = \sum_{j=1}^i a_j - \sum_{j\in S_i} b_j\)。
使用反证法可以证明:
首先,如果将 \(S_{i-1}\) 看作前 \(i\) 天的子问题的解,那么 \(S_{i-1}\) 一定不优于 \(S_i\)——因为在我们的算法中,经过第 \(i\) 天的扫描,要么解集大小增大了,要么 \(V\) 值增大了,要么保持不变,不会变劣。
假设前 \(i\) 天的最优解是 \(T\) 而不是 \(S_i\),则 \(S_i \neq T\),\(|S_i| < |T|\) 或 \(|S_i| = |T| \land V_{S_i} < V_T\)。
那么我们显然会有 \(i \in T\)。因为如果 \(i \notin T\),由于 \(T\) 优于 \(S_i\),而 \(S_i\) 不劣于 \(S_{i-1}\),那么 \(T\) 就优于 \(S_{i-1}\),又因为 \(T\) 也是前 \(i-1\) 天的子问题的解,那么与「\(S_{i-1}\) 是前 \(i-1\) 天的最优解」矛盾。
我们记 \(T - \{i\}\) 为 \(G\)。
如果 \(V \geq b_i\),则 \(i \in S_i\)。因为同时 \(i \in T\) 而 \(T\) 优于 \(S_i\),那么显然 \(G\) 也会优于 \(S_i - \{i\} = S_{i-1}\),矛盾,因此 \(T\) 不会优于 \(S_i\)。
如果 \(V < b_i\),那么很显然 \(|S_i| = |S_{i-1}|\)。
第一种情况,\(|T| > |S_i|\)。因为 \(i \in T\),那么 \(V_G \geq b_i > V_{S_{i-1}}\),而由 \(|T| > |S_i|\) 可得 \(|G| = |T| - 1 \geq |S_i| = |S_{i-1}|\),因此 \(G\) 比 \(S_{i-1}\) 优,矛盾。
第二种情况,\(|T| = |S_i|\) 且 \(i \in S_i\)。则存在至少一个 \(k < i\) 使得 \(k \in S_i, k\notin T\)。因为 \(V_T = V_G + a_i - b_i > V_{S_i} = V_{S_{i-1}} + a_i - b_{i} + \max_{j \in S_{i-1}} b_j\),则 \(V_G - b_k > V_G - \max_{j \in S_{i-1}} b_j > V_{S_{i-1}}\)。又 \(V_G - b_k\) 可以视为 \(G \cup \{k\}\) 的库存量,而 \(|G \cup \{k\}| = |G| + 1 = |T| = |S_i| = |S_{i-1}|\),则 \(G \cup \{k\}\) 比 \(S_{i-1}\) 优,矛盾。
第三种情况,\(|T| = |S_i|\) 且 \(i \notin S_i\)。同样,存在至少一个 \(k < i\) 使得 \(k \in S_i, k\notin T\)。在这种情况下 \(b_i \geq \max_{j\in S_{i-1}} b_j \geq b_k\)。那么 \(V_T = V_G + a_i - b_i > V_{S_i} = V_{S_{i-1}} + a_i\),则 \(V_G - b_k \geq V_G - b_i > V_{S_{i-1}}\)。同第二种的分析可得矛盾。
因此,归纳可得,我们的贪心算法得到的集合 \(S_i\) 是前 \(i\) 天的最优解集合。
UPD 4.19
有一种不那么直观也不那么严谨的理解方法,如果对于严谨性有一定追求但是又没有太多时间的可以尝试理解一下。
如果不需要发生更换,我们就可以直接选择 \(b_i\),那么直接选择必然是最优的。
如果所有已经选择的 \(b_j\) 都比 \(b_i\) 小,那么把 \(b_i\) 换进去显然没有都没有意义。
如果可以进行更换,我们只能将已选的最大的 \(b_j\) 换成 \(b_i\)。除此之外的任何更换毫无意义,因为删去 \(b_j\) 后,\(j\) 之前的位置不可能被影响,\(j\) 之后的位置中没有被选上的位置的 \(b\) 值一定大于 \(b_j\)(因为否则 \(b_j\) 会被替换掉),那么对 \(j\) 之后的位置进行更换不会出现更优的解。
如何输出方案:最终的方案就是优先队列中的所有元素
代码:AC代码
数学
Coprime
数论、暴力、技巧
Coprime - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
要点:当数据的特点是范围小(数值类型)而个数多时,可以考虑对数据大小范围内的所有实数做暴力,而不是对输入的数据做暴力
// 注意到,数组最多有1000个不同的元素,因为a<=1000。对于每个值,存储它所在的最大索引。然后我们可以枚举1000以内所有互质的数,然后再判断这两个数是否在数列中。若在,就将答案更新。
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
void solve()
{
int idx[N]{};
int m;
cin >> m;
for (int i = 1; i <= m; i ++ )
{
int x;
cin >> x;
idx[x] = max(idx[x], i);
}
int ans = 0;
for (int i = 1; i <= 1000; i ++ )
{
if (!idx[i]) continue;
for (int j = 1000; j >= i; j -- )
{
if (idx[j] && __gcd(i, j) == 1)
{
ans = max(ans, idx[i] + idx[j]);
}
}
}
if (!ans) cout << -1 << endl;
else cout << ans << endl;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;
cin >> n;
while (n -- )
solve();
}
位运算
Orray
或运算、暴力、结论
Orray - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
【位运算 暴力】CF1742G Orray - 一扶苏一 的博客 - 洛谷博客 (luogu.com.cn)
要点:算术操作“按位或”是没有进位的,且保证两个数按位或起来一定大于等于原先的两个数,所以有结论:

具体做法:

// 暴力从没有用过的数中找出使得新的前缀或运算结果最大的数,将它输出。做log2(a_max)次即可。最后将剩下的直接输出。
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
void solve()
{
int a[N]{};
bool vis[N]{};
int n;
cin >> n;
for (int i = 0; i < n; i ++ ) cin >> a[i];
int cur_or = 0;
for (int i = 0; i < min(n, 31); i ++ )
{
int mx = 0, idx = 0;
for (int j = 0; j < n; j ++ )
{
if (vis[j]) continue;
if ((cur_or | a[j]) > mx) mx = cur_or | a[j], idx = j; // 特别注意:位运算的优先级比大于号低,要加括号。以后碰到位运算和比较运算符在一起都要加括号,防止出错
}
vis[idx] = true;
cout << a[idx] << " ";
cur_or |= a[idx];
}
for (int i = 0; i < n; i ++ ) if (!vis[i]) cout << a[i] << ' ';
cout << endl;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
int n;
cin >> n;
while (n -- )
solve();
}
Even-Odd XOR
异或、结论、构造
Even-Odd XOR - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
要点:
-
异或运算的定义和运算律
- 定义:
0 ^ 0 = 0, 0 ^ 1 = 1, 1 ^ 0 = 1, 1 ^ 1 = 0 - 运算律:
- 一个值与自身的运算,总是为 false,即
x^x=0 - 一个值与 0 的运算,总是等于其本身,即
x^0=x - 交换律,
x^y=y^x - 结合律,
(x^y)^z=x^(y^z)
- 一个值与自身的运算,总是为 false,即
- 定义:
-
定理:奇数和偶数位置异或和相等的充要条件是全局异或和为 0
证明:设奇数和偶数位置的异或和分别为
a,b,全局异或和为g\(g=0 \Leftrightarrow a\wedge b=0 \Leftrightarrow a=b\)
综上:只需保证全局异或和为0即可
一种构造方式是:
前n-3个数为1,2,3,...,n-3,第n-2个数为\(2^{29}\),第n-1个数为\(2^{30}\),第n个数为所有前n-1个数的异或和。
这种方法可以保证:
-
全局异或和为0,因为前n-1项与第n项的异或和为0
-
每个数互不相同
证明:首先前n-3个数互不相同,且因为n<2e5<2^29,所以前n-1个数都互不相同。\(a_{n-2}是2^{29}级别的,a_{n-1}是2^{30}级别的,\\根据异或运算的定义,a_{n}是2^{29}+2^{30}级别,所以a_{n}比前n-1个数都大\)
#include <bits/stdc++.h>
using namespace std;
void solve()
{
int n;
cin >> n;
int xsum = 0;
for (int i = 1; i <= n - 3; i ++ )
{
cout << i << ' ';
xsum ^= i;
}
cout << (1 << 29) << ' ' << (1 << 30) << ' ' << (xsum ^ (1 << 29) ^ (1 << 30)) << "\n";
}
int main()
{
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
int n;
cin >> n;
while (n -- )
solve();
return 0;
}
搜索
最优配餐
多源BFS,最短路
单源BFS求最短路的原理:
- 建立一个距离数组
d和一个队列q - 起点的
d=0,入队 - 第一轮找到所有与源点距离为1的点
d=1,第二轮找到所有与源点距离为2的点d=2,第三轮找到所有与源点距离为3的点d=3……。因此,每个点第一次被搜到时,它的d值就是到源点的最短距离。 - 适用于网格图之类边权都为1的最短路问题
多源BFS求最短路的原理:
-
建立一个距离数组
d和一个队列q -
所有的起点的
d=0,构成一个起点集合,入队 -
第一轮找到所有与集合距离为1的点
d=1,第二轮找到所有与集合距离为2的点d=2,第三轮找到所有与集合距离为3的点d=3……。因此,每个点第一次被搜到时,它的d值就是到集合的最短距离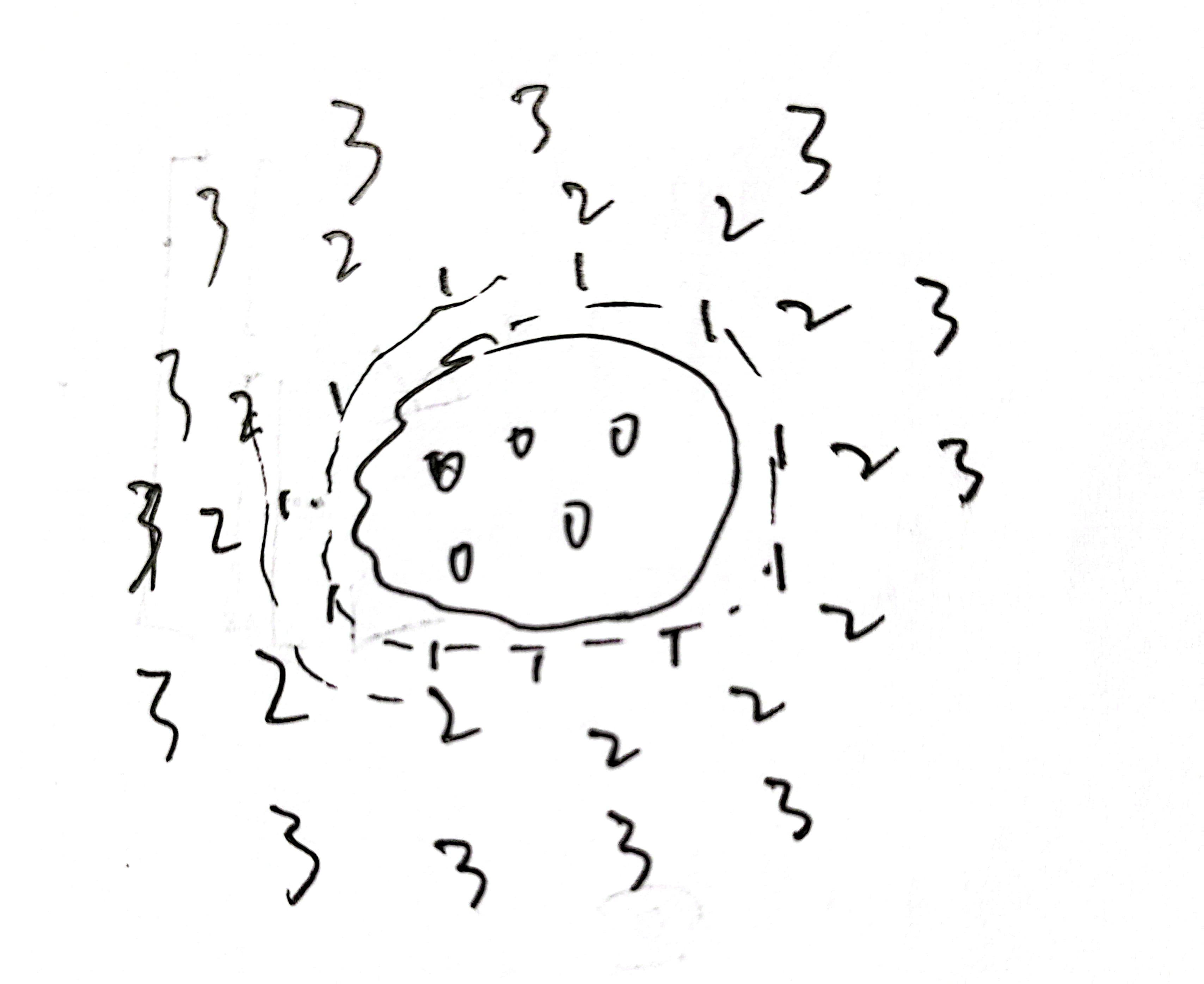
-
因为每次都找到了所有距离集合为k的点,就不存在从某个源点走另一条路到该点更短的情况,因此
d也是该点到起点的距离的最小值。 -
适用于网格图之类边权都为1的最短路问题
游戏
BFS、Flood fill
这道题是经典的BFS在方格图上求最短路的变形题。它的创新之处在于:每个方格能不能走不是不是固定的,而是随时间变化的。设刚开始走的时候是0时刻,障碍方格会在给定的[a, b]时刻不能走,而其他时间可以走。
解析:我们在BFS时,总会维护一个st数组,防止走回头路。一般是一个二维数组st[x][y],当st[x][y]==true时,代表(x,y)走过,不能再走了。在这道题里,一个方格在某段时间不能走,其他时间能走,那也就意味着,从同一个方格不同时刻出发,其结果不同。于是我们应该用一个三维数组来判重,st[x][y][t]=true代表(x,y)点在t时刻走过,不能第二次从同一个点、同一时刻出发。
其他部分和经典的Flood fill算法相同
线段树
祭坛
离散化、线段树
这是一道经典的二维坐标图上离散化+线段树的问题,特征是:
- 给出的数据是二维坐标图上的点
x和y的范围很大,达到1e9级别,而数据个数最多3e5- 所求问题可以转化成对所有的点按从小到大的顺序逐行或逐列扫描,线段树维护的是一维的序列,而对于二维的数据,我们可以通过逐行扫描的方式转化成一维。
要点:
-
答案一定在给出的所有
x和y的组合(x,y)中,因为祭坛的中心是对角线的交点。 -
对于每个可能的点,它的层数是上下左右四个方向的点数最小值,我们要找的就是这个最小值最大的点。
-
根据1和2,有一种
n^2的做法,枚举所有(x,y)的组合。- 如果该点是给出点,跳过。
- 否则,我们可以将每一行的点分别存在一个数组中,做离散化,所枚举到的点的
x在这一行的位置就可以得到该点在这一行左边和右边有多少个点了。对于一个点上下有多少个点同理。一个空间优化的技巧就是保存当前的最优值,只有求出的值不劣于当前最优值的点才保存。 - 这个做法可以得到60分代码
-
另一种思考方式是,我们先对
x做离散化,解决范围过大的问题。然后按照y坐标从小到大的顺序遍历所有行,每一行是所有x的序列,有的x在这一行有给出点,那它们不可能是答案,有的x在这一行没有给出点,那就是可能的答案。对于序列中的每个
x,我们可以维护它们在当前行时上下点数的最小值,作为该x的权值,那我们要做的就是求出整个区间的权值最大值,则是一个区间查询问题。对于序列中的每个x的权值的更新则是一个单点修改问题。而要求能取到最大值的点数,可以在求出最大值后,对每个点设置一个属性,如果该点的值等于最大值,取为1。那所有的点数就是一个区间和问题。
因此可以用线段树来维护。
-
线段树的节点设计
struct Node { int l, r; // 区间的左右端点 int v, c; // v上下的点数最小值,c是否大于最后得到的最优解 }tr[N * 4];
字符串
最佳文章
AC自动机、矩阵乘法、快速幂、状态机DP
题目大意:给定n个模板串,问长度为m的主串中,最多出现多少个模板串(不判重,出现一次算一次),这个被称为重要度
这是一个在AC自动机上做动态规划的问题
-
状态表示
f[i][j]:主串长度为i且最后一个字符位于AC自动机的节点j的所有主串的最大重要度 -
目标
设AC自动机的节点编号为
0~idx,这是建立trie树过程中确定的。那么,要求的就是:max(f[m][0~idx])注意:构造任意主串时,最后一个字符不一定是模板串中出现的字符,也就是不一定在AC自动机中。但是最后一个字符是某个模板串中的字符一定比不是更好,因为如果是,那这个字符还有可能和前面的字符构成某个模板串,不是的话这个字符对重要度没有贡献了。
-
状态转移
f[i][j]是长度为i,最后一个字符位于节点j的主串的最大重要度。下一个字符可能是26个字母中任意一个,则f[i][j]可以转移到f[i+1][tr[j][a~z]]。状态转移方程:比如
f[i][j]是从f[i-1][k]转移过来的,那f[i][j]的重要度就等于前面出现过的模板串个数f[i-1][k],再加上新增的以j为结尾的模板串个数cnt[j],这个cnt[j]是构建trie树时求出来的。而f[i][j]可能会从f[i-1][0~idx]转移过来。于是我们可以构建这样的一个数组
w,w[i][j]表示从AC自动机的节点i转移到节点j,重要度增加了多少,所以w[i][j]=cnt[j]。因为节点i的下一个字符可能是a~z,而下一个字符对应的节点可能相同,所以w[i][j]可能多次出现,我们要统计最大的,w[i][j] = max(w[i][j], cnt[j])。其实枚举下一个字符是a~z就是尝试从i能不能转移到j,如果能转移,cnt[j]是相同的,对w[i][j]没有改变,但是如果不能转移,w[i][j]就等于-inf借助矩阵
w,我们可以写出状态转移方程:f[i][j] = max(f[i][j], f[i - 1][k] + w[k][j]),0<=k<=idx -
矩阵快速幂优化
构造
F(i) = {f[i][0], f[i][1], ...., f[i][idx]},则有F(i) = F(i-1) * w。注意,这里的
*是一种表示方式,并不是常规的矩阵乘法。具体运算方式举个例子:f[i][0]=max(f[i-1][0]+w[0][0],f[i-1][1]+w[1][0]),..,f[i-1][idx]+w[idx][0]就相等于向量
F(i-1)和矩阵w的第一列w[i][0]做运算得到了f[i][0]则目标
F(m)=F(m-1)*w=...=F(0)*w^m,其中的w^m就可以用矩阵快速幂算,那就由原来的m级别的线性递推,直接变成logm级别的快速幂w的大小为(idx+1, idx+1),F的大小为(1, idx+1) -
AC自动机的前缀和优化
cnt[p]在trie树中是以从根节点走到结点p的模板串的个数。我们现在对于节点p,要求的是以它为结尾的所有模板串的个数,而不单单只是从根节点走到它的那个模板串。这可以用前缀和来求,因为以
p为结尾的模板串个数就等于从根节点到p的模板串个数加上这个模板串的最大后缀中所包含的模板串个数。设
s[i]为以节点i为结尾的模板串个数,有s[i]=s[ne[i]+cnt[i]。可以原地前缀和得:cnt[i] += cnt[ne[i]]注意:因为BFS是层序遍历,搜到
i时,ne[i]已经被算出 -
初始化
初始化
F(0)即可。f[0][0]=0合法。其他的f[0][1~idx]不合法,因为主串长度还是0,怎么能走到AC自动机的其他节点呢,因此f[0][1~idx]=-inf -
时间复杂度
模板串总长度为
s,主串总长度为m,模板串个数为n,字符集大小为26构造AC自动机的复杂度:
O(26*s),BFS每个点搜一次,最多s个点,每个点有26个儿子矩阵快速幂的复杂度:
O(s^3 * logm)总复杂度:
O(26*s + s^3 * logm)
构造
Smaller
构造、字符串
Smaller - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
要点:构造算法
不难发现,如果 t 中有一个字符不是 a,那么只要把那个字符移到第一位,就可以满足 s 的字典序小于 t,而如果两个字符串中都只有 a 的话,那就只要比较两个字符串的大小就好了
计算几何
水渠规划
计算几何、点到线段的距离
点到三角形的最短距离就是点到三角形的三条线段的距离中最小的那个。
所以只需分别求出点到三条线段的距离,取最小的那个即可。
矩阵面积并
扫描线、线段树
CCF题目链接-数据量100
模板题-数据量1e5
同类习题
朴素的扫描线的复杂度是O(n^2)
线段树加速复杂度是O(nlogn)
解法一:朴素扫描线
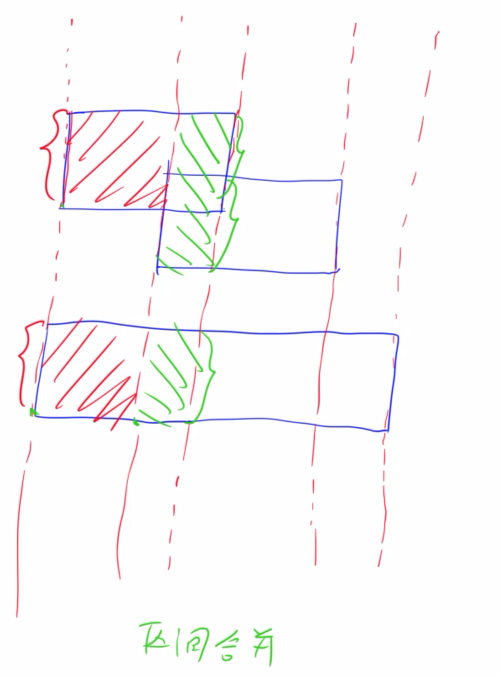
-
对所有x排序去重,每个x就是一条扫描线
-
枚举扫描线(长条),长条内部为若干等宽矩形,只需看竖直方向上的区间(枚举所有矩形,看它竖直方向的区间是否被当前扫描线所截),如果区间有交集,则合并
单个长条的面积=所有合并后区间的长度之和 * 区间宽度
解法二:线段树扫描线
用线段树来维护每个扫描线对应的区间
算法思路:

将所有的x排序去重后,相邻x的长度就是线段树要维护的区间,如上图。
要定义两个结构体
- 线段树的结构体存储区间的左右端点(离散化后的),和该区间对当前扫描线的长度以及被覆盖的次数。
- 扫描线的结构体存储扫描线的区间范围,高度以及是一个矩形的下边还是上边
这个算法处理矩形重叠问题的关键点:
-
扫描线分为上边和下边,下边的标签是
1,上边的标签是-1,分别代表进入矩形和离开矩形。 -
区间的覆盖次数
cnt,当区间的cnt为0时,代表此时该区间对面积没有贡献,长度应该为0,这通过pushup实现。而每次扫描线都会先更新其覆盖范围内区间的cnt,如果一个区间的cnt没有被减为0,代表该区间对该扫描线对应的区间长度有贡献,如果被减为0,则没有。注意:只有区间被当前扫描线完全覆盖,cnt才会被修改cnt的增加和减少都通过使用扫描线的tag做区间修改实现扫描线对应的区间长度通过区间修改的同时使用
pushup函数向上传递实现,最后根节点的len就是总的区间长度单个长条的面积通过宽度*区间长度得到
最后的结果就是单个长条的面积累加
图论
城市通电
最小生成树、超级源点
解析
-
题目有两种费用
- 每个点之间的边的费用
- 建立发电站的费用
-
这是一道最小生成树中超级源点的模板题,核心就是将假设有一个“超级源点”,将建立发电站的费用转化为每个点到“超级源点”的边的费用,则原题就可以转化为求增加了超级源点后的最小生成树的大小和方案。
-
Prim算法求方案:在更新dist变小时distp记录是哪个点让它变小的,那个点就可能是这个点在最小生成树中的一个邻点。最终当一个点纳入最小生成树集合时的distp就是邻点。
AC代码:code
道路与航线
最短路,dijkstra、拓扑排序
P3008 Roads and Planes G - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
题目大意
一张图满足:
- 无向边权值非负,双向
- 有向边权值可正可负,单向,如果存在一条从A到B的有向边,保证不可能通过一些无向边和有向边从B到A(无环)
求一个点到其他所有点的最短路
解析
这题要求的是带负权边的最短路,显然不能直接用Dijkstra。然而Bellman-Ford或SPFA的时间复杂度最坏O(N**M*),尽管这题数据比较老,因此SPFA+SLF可以水过,但是正解并不是如此。
可以发现,图有一个很强的性质:对于无向边,边权总是正的,因此每个无向边联通块是强联通的。而可能的负权边保证不能反向联通,因此把无向边联通块缩点后,得到的就是DAG。这样就可以在块内使用Dijkstra,块间利用拓扑排序更新答案。时间复杂度O(MlogN + M + N)。
正确性
对于每个点,都是通过它的邻点更新它的dist值,块内的Dijkstra用与它无向边相邻的点更新,块间的拓扑排序用与它有向边相邻的点更新,因此最后得到的dist值就是最小的。
对Dijkstra的理解:原来都是在一个图内做dijkstra,从源点S出发更新邻点的dist值。其实该算法的本质就是用一个点的dist值来更新它的所有邻点的dist值,因此块内的dijkstra做法是
- 让块内所有点入队
- 取出dist最小的(不一定是源点),更新它的邻点
- 如果邻点是块内的点,则入队。如此往复,直到队列为空。
- 细节:当一个点从队列中取出来时,它的dist值已经达到最小(有向边和无向边都更新完成)。开一个全局的st数组,将这样的点标记为true,之后再遇到它时跳过。
对拓扑排序的理解:拓扑排序求最短路的状态转移方程是\(dist[son] = min(dist[son], dist[father] + w)\),与dijkstra的更新方式一样。做法是
- 无论邻点是不是块内的点,都松弛。
- 如果是其他块的点,则那一块的入度减1。
- 一个连通块的入度减为0时,入拓扑排序的队列
最长路
拓扑排序
解析
在有向无环图(DAG)中,可以用拓扑排序来找最短路和最长路,复杂度是\(O(n + m)\),边权可正可负。
做法:
- 将dist初始化为0xcfcfcfcf,方便之后的更新
- 把除1以外入度为0的点的出边以及删去它们的出边后产生的新的入度为0的点的出边都删去。
- 如果不删去这些边,而按照拓扑排序的做法将它们入队,可能导致答案路径上的某些点的dist错误,算出来的不是从1出发到n的最长距离
- 如果不删去边,也不加入队列,可能导致答案路径上的某些点的入度不会减为0,不能入队,最终可能导致n号点不能到达
- 在拓扑排序时更新\(dist[son] = max(dist[son], dist[father] + w)\)
AC代码:https://www.luogu.com.cn/record/127326796
I’m stuck!
dfs,反向遍历
这道题的其实就是两次dfs
-
第一次:从起点开始dfs,求出所有能从起点到达的点
-
第二次:从终点开始反向搜索,求出所有到达终点的点
重点:如何用反向搜索判断该点是否能到达终点
解法:当位于(x, y)时,向四个方向搜索,如果(xx, yy)可以到达(x, y),则dfs(xx, yy)
最小花费
点分治、树上倍增、二分
要点:
- 把点分治看成一个加速器,如果能在
T(n)的时间内处理出过根节点的方案,就可以用点分治在T(n)logn的时间内处理出所有方案 - 求每个点到根的路径中第一个比这个点权值小的点——树上倍增
动态规划
厦大GPA
分组背包、dfs、技巧、贪心
题目大意
每门考试成绩为百分制,则分数与绩点对应关系如下:
90~100 4.0
85~89 3.7
81~84 3.3
78~80 3.0
75~77 2.7
72~74 2.3
68~71 2.0
64~67 1.7
60~63 1.0
0~59 0.0
某位同学一共参加了4门考试,给定四门考试的总分,请问在最优情况下,4门考试绩点的和最高是多少?
解析
这道题有两种做法
-
直接深搜枚举四个数,可以选择的优化方案
- 从大到小枚举四个数,保证方案不重复枚举
- 当\(score + 4 * (4 - u) <= ans\),返回,最优化剪枝
- 当所剩分数<=0时更新答案返回
云剪贴板 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
这个做法的时间是\(581ms\)
-
看成有4个组和一个容量为总分的背包,每组可选的物品是分数。体积是分数值,价值是对应的绩点,每组只能选一个,求最大价值。这是一个分组背包问题。
-
普通写法:每组的物品就是从1分到100分,用函数算出对应的GPA即可。\(157ms\)
-
技巧与优化:注意到题目中的分数在一个区间内的价值相同,那么每次只需要枚举每个区间的最低分数即可。这样既能保证价值最大,又为其他组空出尽可能多的空间,是最优解。并且这种方式可以查表实现,大大提速。\(4ms\)
-
有趣的数
数位dp
解析:
这是一道数位dp的问题,总体的思路是第n位的结果可以利用前n-1位的结果
首先,通过分析可得,第一位肯定是2
则符合条件2和3的数有6种情况
- 只含2
- 含2,3
- 含2,0
- 含2,0,1
- 含2,0,3
- 含四种数字
状态表示:dp[i][j],位数为i,状态为j的合法(符合条件2和3)的数的个数
目标:dp[n][6],不仅符合条件2和3,还符合条件1
状态转移:
-
对状态1:
dp[i][1]=1,全为2只有一种情况 -
对状态2:
dp[i][2]=dp[i-1][1]+dp[i-1][2]含2、3的数可以由只含2的数在末尾填上3得到,或者由含2、3的数在末尾填上3得到(不能填2)
-
对状态3:
dp[i][3]=dp[i-1][1]+dp[i-1][3]*2含2、0的数可以由只含2的数在末尾填上0得到,或者由含2、0的数在末尾填上0或2得到
-
对状态4:
dp[i][4]=dp[i-1][3]+dp[i-1][4]*2同理,状态4的数不能填0
-
对状态5:
dp[i][5]=dp[i-1][2]+dp[i-1][3]+dp[i-1][5]*2同理,状态5的数不能填2
-
对状态6:
dp[i][6]=dp[i-1][4]+dp[i-1][5]+dp[i-1][6]*2同理
边界:dp[0][i]=0
无线网络
图上DP,最短路
这道题是一道在图上做DP的问题,我想到了怎么用邻接表建图,但是DP的思路我没想到
解析
-
状态表示:
dist[i][j]表示从起点到i号路由器,图中增设的路由器数量为j时的最短距离 -
目标
\[min(dist[2][j]),j\in[0, k] \] -
状态转移
\[对于i\notin [n+1, n+m],dist[i][j] = min\{dist[邻点][j]\} + 1 \\ 对于i\in [n+1, n+m],dist[i][j] = min\{dist[邻点][j - 1]\} + 1 \]第二种情况,dist[邻点][j-1]中的j-1个增设路由器,加上本身,刚好 j 个
当用邻点更新时,应该使用公式
\[dist[i][j + 1] = min\{dist[邻点][j]\} + 1 \] -
边界:
dist[1][0]=0,起点到自身,新增0个路由器时的最短距离为0 -
DP实现和初始化:实现状态转移的方式可以选择BFS,初始状态
(1,0)入队,每次取出队头,队头的邻点入队,并且只有自己更新了,才能去更新邻点,所以只用dist[i][j]变小了,(i,j)才能入队去更新其他点。因此我们需要对dist数组初始化为无穷大,这样每个新搜索到的dist[i][j]必定会减小,就可以入队了。
拼图
状压DP、矩阵乘法、快速幂
这道题和蒙德里安的梦想很像,是一道状压DP的问题
因为m<=7,因此我们选择用二进制表示一行的状态。一行中,如果某一位为空,用0表示,不空用1表示,则一行的状态可以用0~2^m-1的十进制表示
状态表示:f[i][j]表示第i行的状态为j的方案数
目标:f[n][2^m-1]表示第n行都填满的方案数
状态转移方程:
-
第
i行的状态可以从第i-1行转移过来,求一个转移矩阵w。w[i][j]表示当前行的状态为i,下一行的状态为j的方案数 -
f[i][j]=f[i-1][k] * w[k][j], 0<=k<=2^m-1,第i行的状态为j可以从第i-1行状态为k转移过来。 -
矩阵快速幂加速状态转移
如果不加速,状态数有
n*(2^m-1)个,转移数有2^m-1个,时间复杂度有n*(2^m-1)^2,会超时。我们定义一个向量
F[i]:F[i]=(f[i][0], f[i][1], ..., f[i][2^m-1]), 1*(2^m)可以发现,每次的状态转移就是
F[i]=F[i-1]*w,这个展开即可证明。递推得:
F[i]=F[0]*w^i,则F[n]=F[0]*w^n,其中f[n][2^m-1]=F[n][2^m-1]因此,我们只需根据题意初始化边界
F[0],再用矩阵快速幂在logn的时间内算出w^n,两者相乘即可在logn的时间内算出f[n][2^m-1]了。
边界:f[0][2^m-1]=1, 其余f[0][i]都为0,第一行的图形不能突到第0行去,因此第0行只有全为1这一种状态,方案数为1,其余的状态的方案数必须是0
时间复杂度:
- 转移矩阵用
dfs求,最多有(2^7-1)^2=16129 log1e15<50,不会超时
转移矩阵的dfs实现:
通过dfs,寻找转移矩阵。now是当前行的状态,从0遍历到2^m - 1,next是下一行的状态,index是当前行即now的第index个方格,从0开始,到m-1。当index=m时,说明当前行已经填充满,此时的next的值,代表填充完now可以转移到的状态。
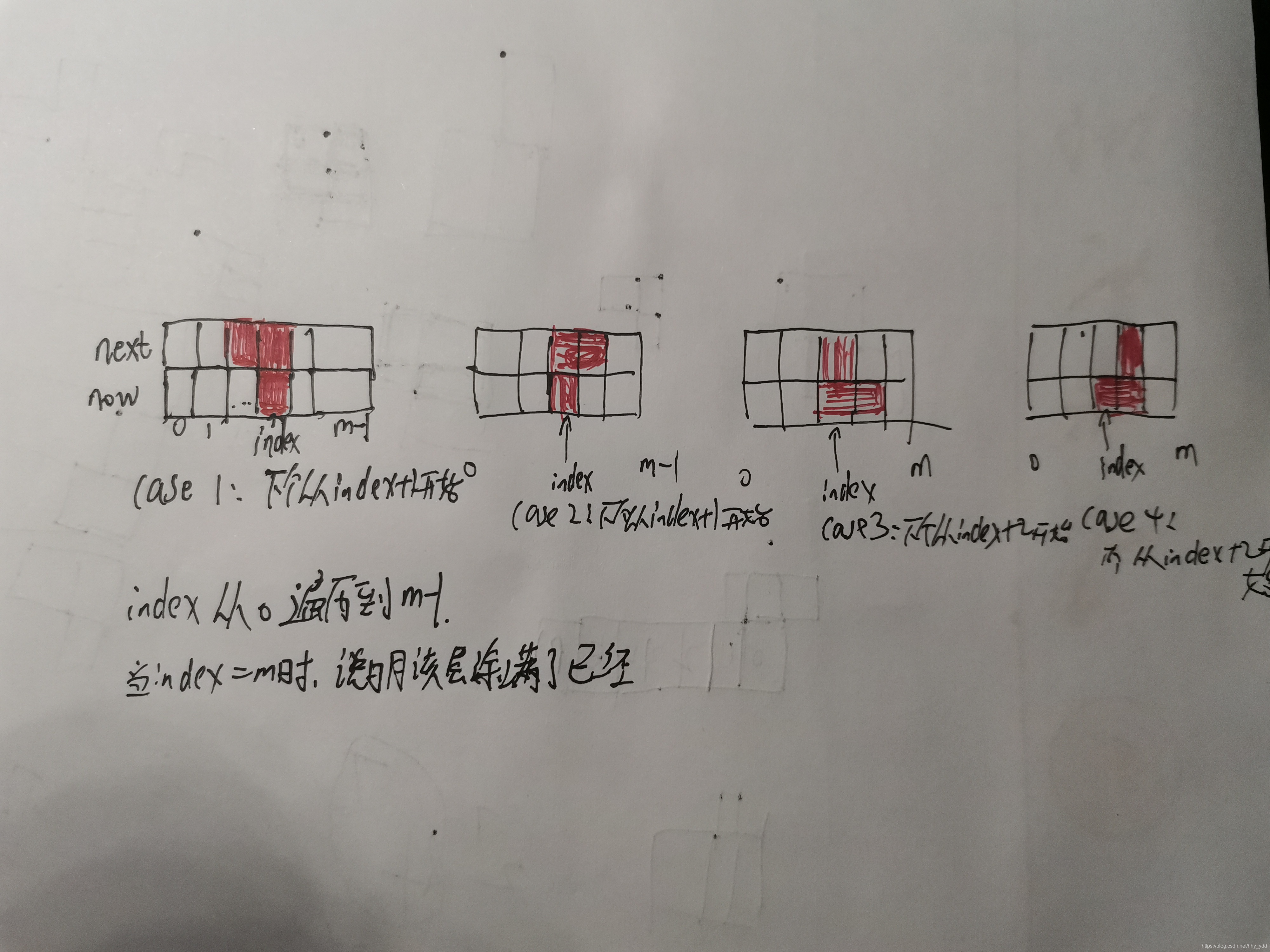
股票买卖系列
状态机DP
最多交易一次
特点:最多交易一次
解法:既然只能交易一次,一共1~n天,如果在第i天买了股票,要获得最大利润,肯定要在i+1~n天中股票价格最高的那天出售。
算法实现:维护一个后缀数组suffix,suffix[i]存的是i~n的股票价格最大值。然后从第一天开始遍历,第i天购买股票的最大利润是suffix[i+1]-prices[i]。
不限交易次数
分析:相比于上一题,从最多交易一次变成可以无限次交易了,用状态机DP来解
解法
-
状态表示
f[i][0]:第i天结束,手中没有股票的情况下的最大利润f[i][1]:第i天结束,手中有股票的情况下的最大利润 -
状态转移方程
要点:第
i-1天的结束就是第i天的开始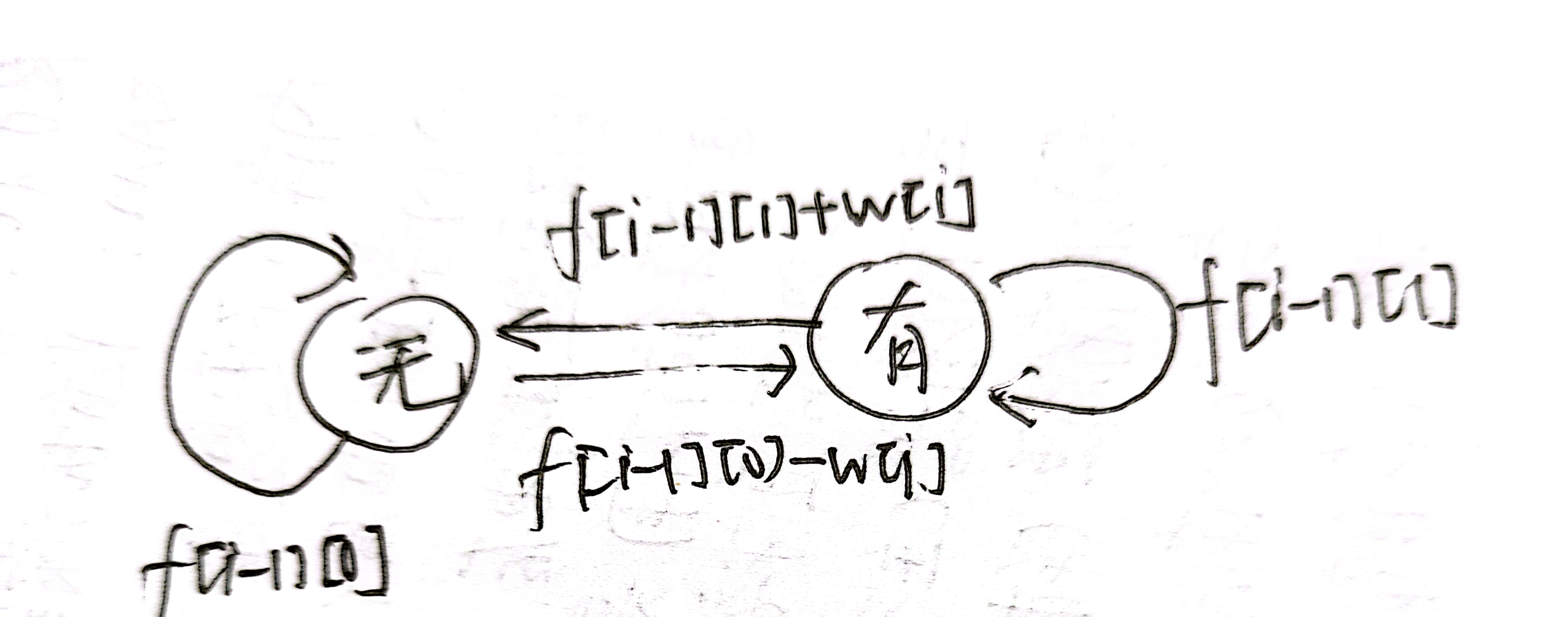
分析:
-
第
i天结束时手中没有股票,有两种情况。一是前一天手中没有股票且今天没有交易,那利润不变;二是前一天手中有股票今天卖出去了,那利润加上今天的股票价格。所以有:f[i][0] = max(f[i-1][0], f[i-1][1]+price[i]) -
第
i天结束时手中有股票,有两种情况。一是前一天手中有股票且今天没有交易,那利润不变;二是前一天手中没有股票今天买了股票,那利润减去今天的股票价格。所以有:f[i][1] = max(f[i - 1][1], f[i - 1][0] - price[i])
-
-
边界条件
第0天结束,也就是第1天开始时,不可能持有股票,因此不能从
f[0][1]转移过来,要将f[0][1]置为负无穷;第1天开始时不持有股票是合理的,此时利润是0,因此f[0][0]=0 -
答案
第n天结束时,如果手中还有股票,那就是之前买了没卖出去,亏了。因此我们取第n天结束时手中没有股票的情况。答案是
f[n][0]
最多交易K次
分析:与上一题相比,限制了最多交易K次,因此我们要加一维状态来记录交易次数
解法
-
状态表示
f[i][j][0]:第i天结束,交易j次,手中没有股票的情况下的最大利润f[i][j][1]:第i天结束,交易j次,手中有股票的情况下的最大利润注意:买入卖出算一次交易,我们在买入的时候交易次数加1,卖出时交易次数不变
-
状态转移方程
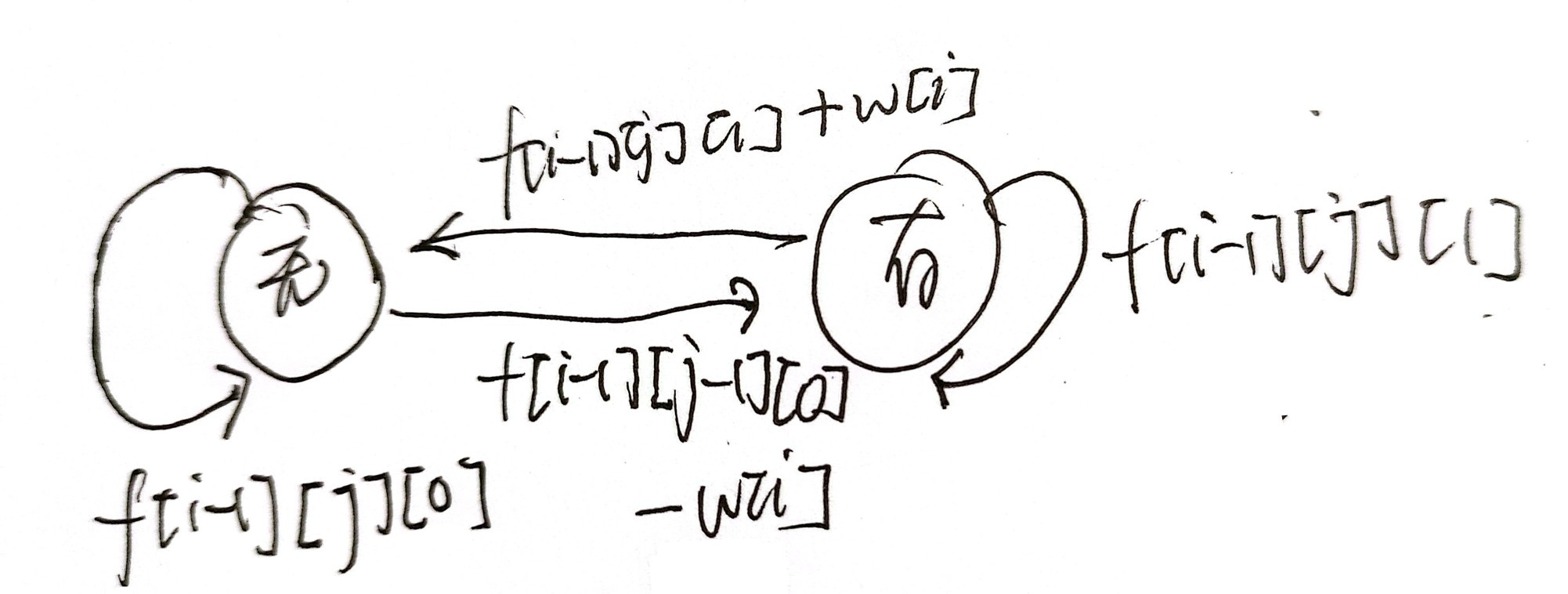
分析:
-
第
i天结束时手中没有股票,交易了j次,有两种情况。一是前一天手中没有股票且今天没有交易,那利润不变,交易次数不变;二是前一天手中有股票今天卖出去了,那利润加上今天的股票价格,交易次数还是不变。所以有:f[i][j][0] = max(f[i - 1][j][0], f[i - 1][j][1] + price[i]); -
第
i天结束时手中有股票,交易了j次,有两种情况。一是前一天手中有股票且今天没有交易,那利润不变,交易次数不变;二是前一天手中没有股票今天买了股票,那利润减去今天的股票价格,交易次数加1。所以有:f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j - 1][0] - w[i]);
等价变形
-
因为我们在用数组写法时,会枚举交易次数从
0~k次,那j-1会越界。我们做一个等价变形,令j->j+1,因此有:f[i][j+1][0] = max(f[i - 1][j+1][0], f[i - 1][j+1][1] + price[i]);f[i][j+1][1] = max(f[i - 1][j+1][1], f[i - 1][j][0] - price[i]); -
这样写的话,
j在循环变量里还是正常枚举0~k
-
-
边界条件
- 第0天结束,第1天开始时,交易次数只能是0,大于0的不合法。
- 第0天结束,第1天开始时,不能持有股票。
- 任何一天的交易次数都不能是负数
- 第1天开始时,交易0次,不持有股票是合法的,利润为0
注意:我们已经把
j向右偏移了一个,写的时候要注意 -
答案
答案就是第
n天结束时,不持有股票,交易次数在0~k次的最大值
有冷冻期
分析:这道题在不限交易次数的情况下规定卖出后的第二天不能买入
状态转移
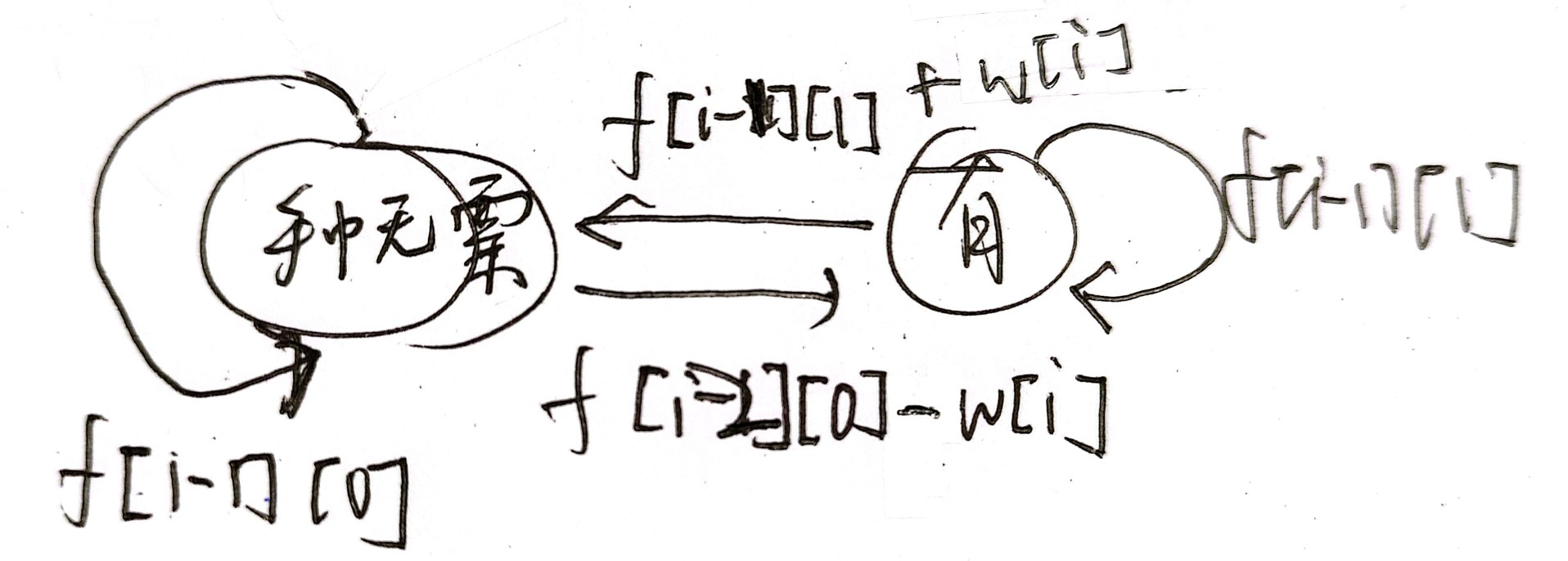
-
加了冷冻期后,要从手中无票的状态转移到手中有票,就必须是前天结束时手中无票,而不能从昨天手中无票转移过来,因为昨天卖了股票后,今天就不能买股票了。如果考虑股票不是昨天卖的,那就是前天结束时手中无票的情况,所以从前天转移是合理的。
-
第
i天结束时手中没有股票,有两种情况。一是前一天手中没有股票且今天没有交易,那利润不变;二是前一天手中有股票今天卖出去了,那利润加上今天的股票价格。所以有:f[i][0] = max(f[i-1][0], f[i-1][1]+price[i]) -
第
i天结束时手中有股票,有两种情况。一是前一天手中有股票且今天没有交易,那利润不变;二是前天结束时手中没有股票今天买了股票,那利润减去今天的股票价格。所以有:f[i][1] = max(f[i - 1][1], f[i - 2][0] - price[i])
等价变形
-
i从1~n枚举,i-2会越界,因为我们将i替换成i+1,则当循环变量i=1时就不会越界了。循环变量i还是从1~n枚举 -
因此有:
注意:当循环变量为
i时,买卖的是第i天的股票,所以price数组下标仍为if[i + 1][0] = max(f[i][0], f[i][1] + price[i]);f[i + 1][1] = max(f[i][1], f[i - 1][0] - price[i]);
边界条件:第0天结束,也就是第1天开始时,不可能持有股票。由于i右移,所以第0天的下标是1,f[1][1] = -inf
答案:第n天手中无票,由于偏移了,第n天的两个状态存在下标n+1的位置,因此答案是f[n+1][0]
有手续费
分析:这道题在不限制交易次数的情况下,规定每次交易都要缴纳手续费c元
解析:其实只需要在状态转移计算利润是多减去一个c即可。由于买卖算一次交易,我们就在买入股票时减去手续费即可,卖出股票时不用减了,因为一次交易只需要缴纳一次手续费。
只需修改第i天手中有票的状态转移为:
f[i][1] = max(f[i - 1][1], f[i - 1][0] - price[i] - c);
原来是
f[i][1] = max(f[i - 1][1], f[i - 1][0] - w[i]);
字典序编码
区间DP
分析题目:
- 01编码且任何一个单词的编码(对应的01串)不是另一个单词编码的前缀,说明:每一个合法的编码都对应一颗二叉树,树的叶子节点就对应每一个字符。
- 编码满足字典序,而二叉树的所有叶子结点都分布在根节点的左右子树上,所以只要前一半字符的叶子节点在左子树,后一半在右子树,就能保证前一半字符编码的字典序比后一半的小。而在子树中同理。因此:整个问题就可以不断分成左右两个区间解决。原问题的解可以被划分为子区间的解,这就可以用区间DP来做。
状态表示:f[i][j]表示[i,j]区间内的字符字典序编码的最小长度
状态转移:f[i][j] = f[i][k] + f[k][j] + s[r] - s[l - 1]。其中左区间的解+右区间解还要在加上增加了一条边后全部节点的编码长度+1的代价。
坏掉的项链
动态规划
https://www.luogu.com.cn/problem/P1203
算法流程:
- 求出每个
i,包括自己,往左取红色、蓝色,往右取红色、蓝色分别能取多少 - 答案就是枚举所有的断点,取最大的。值得注意的是,在求1时,没有考虑到左右两边取的珠子重复的情况。但是,如果重复,则最后取的珠子之和一定大于项链长度,所以跟项链长度取一个min就能排除互相覆盖情况对答案正确性的影响。
- 在代码实现中,并没有一定要保证正确的初始条件,比如第一个珠子往左取的个数。但是,可以保证
lR[1]和lR[n + 1]已经有一个是对的。可以分析一下,加入第一个珠子是蓝色,则lR[1] = 0是对的,那后面的递推也是对的。如果第一个珠子是白色或红色,最后一个珠子是蓝色,那lR[1] = 1是对的。如果第一珠子是红色或白色,最后一个珠子也是红色或白色,那lR[1] = 1是错的,但是在1~n中,出现了一个蓝色,那后面的lR[j~n]就是对的,从而lR[n + 1] = lR[n] + 1也是对的。如果中间没有断开,那lR[n+1]=n+1,超过了n,那其实lR[1]应该是n,但是lR[n+1]已经大于n,所以最后求答案时,不影响正确性。因此这样的递推方式可以得到正确的答案。 - 最后因为要保证用到正确的
lR、rR、lB、rB数组的值,所以应该要枚举1~2*n-1作为断点的左边。
大朋友的数字
最长不下降子序列
https://www.luogu.com.cn/problem/P2008
这道题的创新点在于要找到编号字典序最小的方案。
做法1:
- 先求出所有以
a[i]为结尾的最长不下降子序列的长度f[i] - 对于每个
a[i],再次枚举它前面的数字,如果有a[j] <= a[i] && f[j] + 1== f[i],说明a[j]就是在f[i]的所有方案中倒数第二个字符最小的,直接跳出。sum[i] = sum[j] + a[i]
做法2:
分析:
在求f[i]的过程中,我们会枚举a[i]前面的所有数a[1~i - 1]
如果a[j] <= a[i]
-
f[j] + 1 < f[i],不是最优解,跳过 -
f[j] + 1 == f[i],那么以a[j]为结尾的子序列的方案的编号字典序会比当前的a[j_1]的小吗?不会。解释一下,已知j_1 < j、f[j] == f[j_1]- 如果
a[j_1] <= a[j],则a[j]的子序列可以包含a[j_1]的子序列,那f[j]不可能等于f[j_1],大前提就不成立 - 如果
a[j_1] > a[j],那比a[j]小的,一定比a[j_1]小,则以a[j_1]为结尾的子序列的编号字典序不可能比a[j]的大,因为假如a[j]的前几个元素的编号更小,a[j_1]完全可以也用这几个元素。 - 综上,
f[j] + 1 == f[i]的情况不会改变当前的方案
- 如果
-
f[j] + 1 > f[i],优于当前方案,更新f[i] = f[j] + 1,sum[i] = sum[j] + a[i]
最大子段和
动态规划
https://www.luogu.com.cn/problem/P1115
给出一个长度为 n 的序列 a,选出其中连续且非空的一段使得这段和最大。
状态表示:f[i]表示以a[i]为结尾的最大子段和
状态转移:以a[i]为结尾的子段,只有两种可能,包括前面的a[i - 1]或者只有它自己。如果包括前面的a[i - 1],那最大子段和就是a[i - 1]的最大子段和f[i - 1]加上a[i],否则就等于a[i]。即f[i] = max(f[i - 1] + a[i], a[i])
网络流
货物调度
最小费用最大流、网络流
解析
建图:
-
点集:每个城市每一天建一个点,一共
n*7个点,还有一个源点、一个汇点 -
边集:
-
由源点指向每个点的边,表示该城市这一天的生产量
a_ij,容量为a_ij,费用为0 -
由每个点指向汇点的边,表示该城市这一天的消耗量
b_ij,容量为b_ij,费用为0 -
每个点指向下一天的点的边,表示货物在仓库里过夜,留给下一天,容量为
v_i,费用为w_i,注意星期天要指向星期一 -
如果两座城市之间存在通路,建立由城市a的第
i天的点指向城市b的第i天的点的边,表示在第i天从城市a运输货物到城市b,容量为inf,费用为c_k。同时,因为道路是双向的,还要建立反向边。注意:这里的反向边不是残留网络中的反向边,因此a和b之间在流网络中实际有4条边
-
-
网络流问题的关键在于找到原问题的任意一个方案与可行流的对应关系。
在这道题中,一个城市的当天货物的流入就对应了产量、前一天留下的还有其他城市运过来的,货物的流出就对应了消耗、留给下一天还有运给其他城市的。因此建立的流网络的可行流和方案是一一对应的。
-
目标:从源点指向每个点的边表示生产量,这些边的
流量=容量,是满流边。根据可行流流量的定义可知,每一个方案对应的可行流就是最大流。并且我们还要求费用最少,也就是找最小费用流。总结:找最小费用最大流,用EK算法


 浙公网安备 33010602011771号
浙公网安备 33010602011771号