汉诺塔问题的一些思考

汉诺塔问题，解决方案和思想：

吧n-1个盘从A杆移动到B杆，已C杆为辅助杆；

把第n个盘从A杆移动到C杆；

把n-1个盘从B杆移动到C杆，以A为辅助杆。

代码：

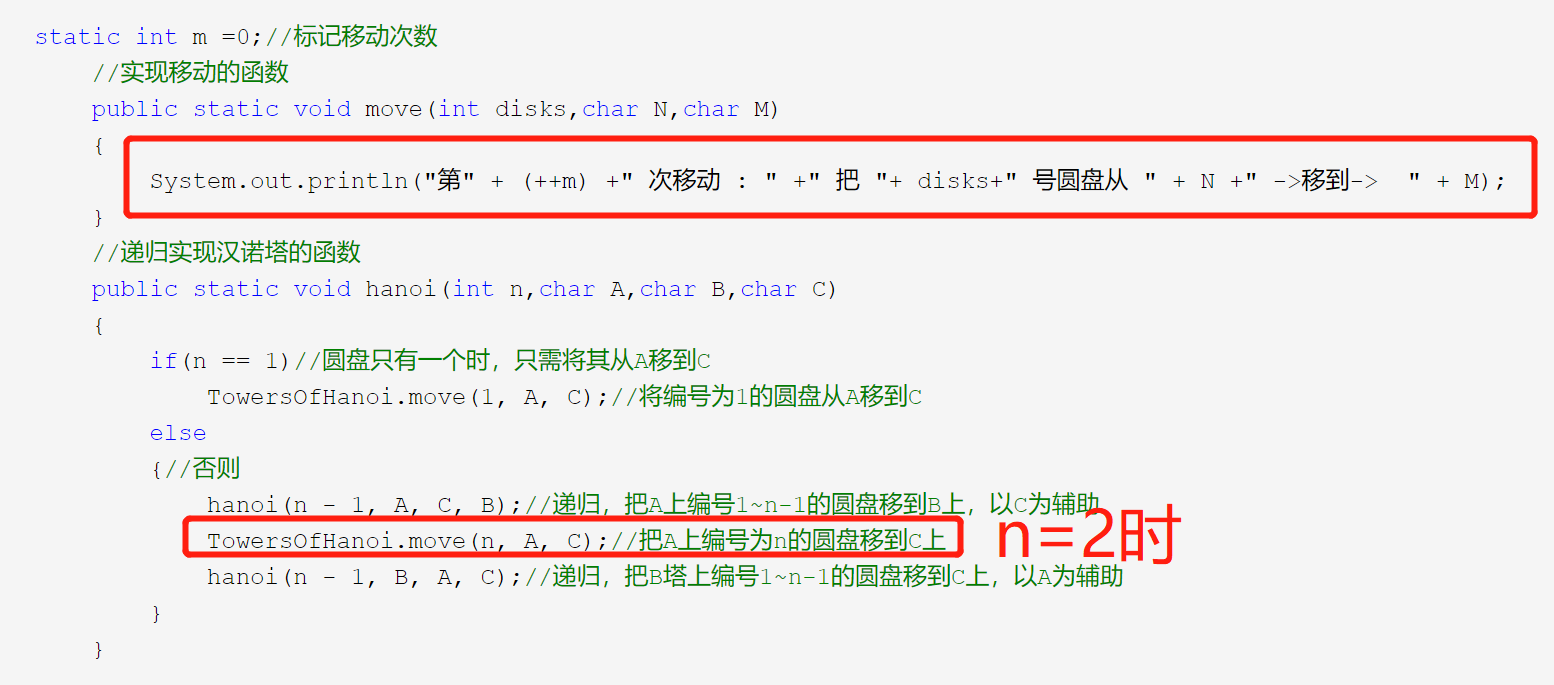
static int m =0;//标记移动次数
    //实现移动的函数
    public static void move(int disks,char N,char M)
    {
        System.out.println("第" + (++m) +" 次移动 : " +" 把 "+ disks+" 号圆盘从 " + N +" ->移到->  " + M);
    }
    //递归实现汉诺塔的函数
    public static void hanoi(int n,char A,char B,char C)
    {
        if(n == 1)//圆盘只有一个时，只需将其从A移到C
            TowersOfHanoi.move(1, A, C);//将编号为1的圆盘从A移到C
        else
        {//否则
            hanoi(n - 1, A, C, B);//递归，把A上编号1~n-1的圆盘移到B上，以C为辅助
            TowersOfHanoi.move(n, A, C);//把A上编号为n的圆盘移到C上
            hanoi(n - 1, B, A, C);//递归，把B塔上编号1~n-1的圆盘移到C上，以A为辅助
        }
    }

思想和代码很直观，但忍不住模拟具体运行流程时，作者陷入一个误区：
　　
若要将n =1盘移动到C杆，递归return会n=2函数体又如何将n=2盘移动到C杆？

 其实这里的形参和实参并未对应：

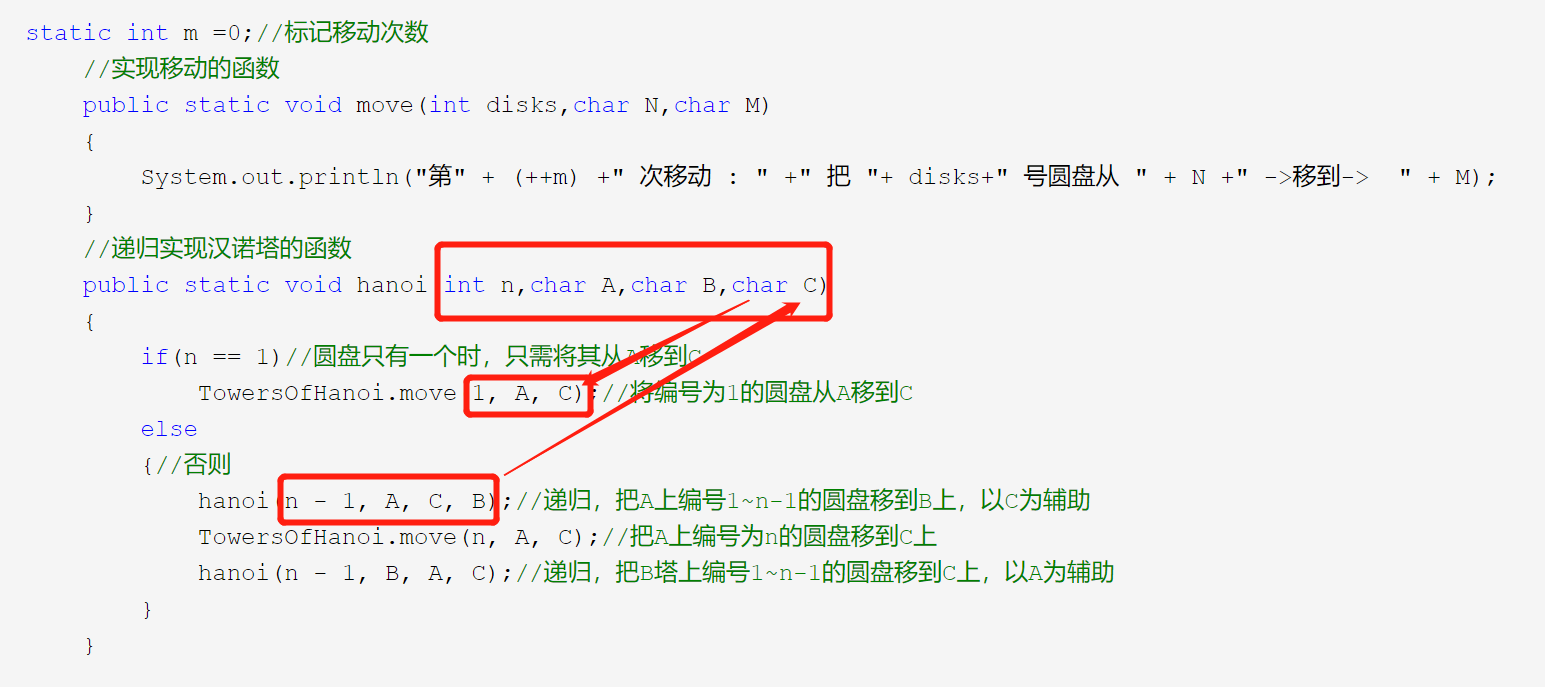
 若递归到n=2盘时目标杆是C杆，即要把n=2盘移动到C杆，递归调用函数传参时目标杆是B杆，即下一次函数调用，目标杆是B杆，即是将n=1盘移动到B杆。

 

 n=1盘并不一定是移动到C杆，有可能是移动到B杆，取决于n=2盘要移动到的目标杆是B还是C，这又由n=3盘的目标杆决定，依次往下直到n盘。

 

可以看到每个盘移动到的目标杆是交叉的，模拟一下就是：

（仅是算法流程的第一步）

n盘→C杆

则：

n-1盘→B杆

n-2盘→C杆

...

直到确定n=1盘第一步是到B还是C杆。

 

 

尝试用人脑模拟递归流程一不小心就出错...