Kruskal重构树学习笔记

算法基本概念

\(Kruskal\) 重构树是一种巧妙处理图上边权限制的算法，用某种方法建立出一颗具有特殊性质的树，通过树上的一些操作巧妙处理图上的限制，用起来感觉真的挺妙的，把二者很完美地结合了起来。

主要思想基于 \(kruskal\) 求最小生成树的方法，二者的构建过程是比较相似的，一般地，我们按以下步骤来对一个图构建 \(kruskal\) 重构树。

先按照边权从小到大排序，用并查集维护连通性，若当前的边 \(u->v\) 边权是 \(w\) ，且 \(u,v\) 不属于同一联通块，就新建一个结点 \(cnt\) ，由 \(cnt\) 向 \(u,v\) 当前并查集维护的根节点连一条边，新建的节点作为新的联通块中的根节点，按照这个过程考虑完所有的边之后，得到的就是原图的 \(kruskal\) 重构树了。

以上大概是一些算法概念和定义的介绍，如果读者感觉不知所云或者不知道怎么运用，请继续看下去，下面我们通过一些例题来感受重构树的精妙所在。

里面用到的结论，笔者也会进行一些感性的证明，让读者可以更好地理解。

[LOJ137] 最小瓶颈路 加强版

给定一个 \(n\) 个点 \(m\) 条边的无向连通图，编号为 \(1\) 到 \(n\) ，没有自环，可能有重边，每一条边有一个正权值 \(w\) 。

给出 \(q\) 个询问，每次给出两个不同的点 \(u\) 和 \(v\) ，求一条从 \(u\) 到 \(v\) 的路径上边权的最大值最小是多少。

\(1\le n,m \le 1e5\) , \(1\le q \le 1e7\)

在没有学习本算法之前，一个比较自然的想法是，考虑贪心，开始所有点不连通，我们由小到大对边进行枚举，枚举到一条边后联通它所连接的两个节点，并查集维护一下连通性，枚举到某条边后 \(𝑢,𝑣\) 联通，那么这条边便是它的瓶颈路。

证明：其实此结论比较显然，考虑当前这条边，是第一次使得 \(u,v\) 两点联通，且按照边权排序，一定不会比之前的边权小，也不会比之后的边权大。那这条边当然是使得两点联通的一条合法路径上的最大值，之后的路径也不会比这个值更小，所以第一次使得两点连通的边就是这两个点的路径上最大值的最小值。

证毕。

上面这个过程就是我们使用 \(kruskal\) 算法求最小生成树的过程，于是可以得出，瓶颈路(即某两点路径中最大边权的最小值)一定在原图的最小生成树上，那我们可以直接找出最小生成树，然后倍增查询两个点的简单路径上边权最大的一条边。

时间复杂度 \(O((n+q)logn)\) ，如果 \(1\le q\le 1e5\) ，那么可过。

但是本题不可过，于是考虑重构树优化，现在我们考虑重构树的一些性质。

这是一棵二叉树。

叶子节点代表原图的点,非叶子节点表示原图的一条边。

对于所有非叶子节点,其点权小于父亲节点的点权(可以理解为一个小根堆)。

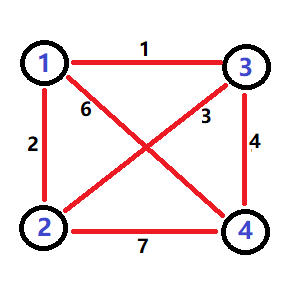
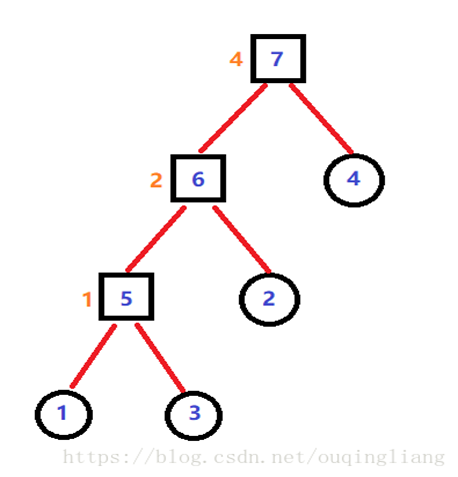
(图是我盗的(doge))

这样做的话， \(u,v\) 两点间路径的最大边权最小值即为 \(LCA(u,v)\) 点权。

证明：易得所有点权都是最小生成树的边权(根据求解过程，显然)，此处运用上文已经证明的结论，当按照从小到大顺序加入边使得 \(u,v\) 刚好连通时，此边为瓶颈路，当加入 \(LCA(u,v)\) 这个点时， \(u,v\) 确实是首次连通的，于是结论成立。

证毕。

利用树的欧拉序加上 \(ST\) 表维护深度，但是注意系统自带的求 \(log\) 的函数不是严格 \(O(1)\) ，是常数时间，需要预处理，可以做到 O(1) 查询 \(LCA\) ，这个算法很简单，网上也有很多讲解，故在此不作赘述。

于是时间复杂度变成 \(O(q+nlogn)\) ，可以通过本题。

[NOI2018]归程

笔者注：这道题揭示了重构树处理图限制的一个常用模型，算是一个不太模板的模板题。

一个 \(𝑛\) 个节点，\(𝑚\) 条边的无向连通图(节点的编号从 \(1\) 至 \(𝑛\) )，我们依次用 \(𝑙,𝑎\) 描述一条边的长度，海拔，所有海拔不超过水位线的边都是有积水的，有 \(𝑄\) 天,每一天知道出发点 \(𝑣\) ,以及当天的水位线 \(𝑝\) 。

\(1\le n\le 2e5\) ，\(1\le m,q\le 4e5\)

每一天，出发点都拥有一辆车。这辆车由于一些故障不能经过有积水的边。可以在任意节点下车，步行经过有积水的边。但车会被留在下车的节点并不会再被使用。

每一天车会在新的出发点被准备好,不能利用之前在某处停放的车，每天操作独立。在完成回家这一目标的同时，最小化步行经过的边的总长度。

我们思考，题面有限制允许走的边权大小，那么看到这个限制，我们自然想到用重构树去优化。

我们按照边权从大到小排序，建立 \(kruskal\) 重构树，考虑一个点 \(u\) ，这个点的海拔是在水位线以上的，那么该点的子树内，所有的叶子节点都可以互相开车到达。

证明：按边权从大到小建树，于是点权随着树深度递增而递增，由上文已经证明的结论，每两点的 \(LCA\) 处点值是两点的路径的最小边权最大值，也就是说在 \(u\) 的子树内，任意点都存在一条路径，这条路径上的最小边权都高于 \(u\) 点的值，亦即，高于水位线，故可以开车(没有代价)到达。

证毕。

于是，我们只要找到一个点 \(x\) ，这个点的海拔刚好高于水位线，但它的父亲节点海拔低于水位线，此时这个点的子树叶子节点互相可以开车到达，且和另外任何一个重构树的叶子不可开车到达。

形式化地，\(height[x]>p\) 且 \(height[father[x]] \le p\) 。

这个点显然可以直接倍增向上找，因为值是单调的。

然后，我们最终要求的是到 \(1\) 号节点的最小值，我们已经知道了从起点开始可以开车到哪些结点，只需求出每个起点可以开车到达的点到 \(1\) 号节点的最短路即可，在这些点中选出到终点最短路最小的即可，这个可以用 \(Dijkstra\) 算法和堆优化，在 \(O(nlogn)\) 时间内预处理。

有 \(T\) 次询问，最后的时间复杂度是 \(O(Tnlogn)\) 的。

[2020FZ校测]神奇的花园

给定一张 \(n\) 个点， \(m\) 条边的无向图，每个点有 \(c_i\) 种类的花无限朵。

有 \(q\) 次询问，每次询问给定 \(a_i，b_i\) ，表示从点 \(a_i\) 开始，只能走边权不超过 \(b_i\) 的边，此时在可以走到的所有点采一朵花，求采到的花里数量最多的是哪种。

看到这个边权不超过 \(b_i\) 的限制，发现和上一题的条件十分相似，考虑重构树。

于是按边权从小到大建树，从起点开始向上倍增找到最上面的合法节点，于是可以走到的点为这颗子树内的叶子。

把子树的 \(DFS\) 序求出来，转换为区间上的问题，等价于求区间众数即可，可以分块求出，具体在此不作赘述。

参考文献

西南大学附属中学.冯嘉一.《 \(kruskal\) 重构树与可持久化 \(kruskal\) 》