二分查找与二分答案
二分查找
也叫做折半查找,要求查找的数据结构必须是线性的,并且是有序的
二分查找的时间复杂度: \(\log_2n\)
推导:
因为二分查找每次排除掉一半的不适合值,所以对于个元素的情况:
一次二分剩下:n/2
两次二分剩下:n/4
m次二分剩下:n/(\(2^m\))
在最坏情况下是在m次二分排除到只剩下最后一个值之后得到结果,即
n/\(2^m\)=1
所以由上式可得:\(2^m=n\)
进而可求出时间复杂度为:
\(\log_2n\)
模板
左闭右闭写法
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6+10;
int n,x,l,r,mid;
int a[maxn];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
scanf("%d",&x);
//Binary Search
l=1;r=n;
//如果区间内有值
while(l<=r)
{
mid=(l+r)/2;
if(a[mid]>x) r=mid-1;
if(a[mid]<x) l=mid+1;
if(a[mid]==x)
{
printf("%d\n",mid);
return 0;
}
}
printf("-1\n");
return 0;
}
左闭右开写法
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6+10;
int n,x,l,r,mid;
int a[maxn];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
scanf("%d",&x);
//Binary Search
//左闭右开的核心理念就是右边是取不到的 即r的下标是不在讨论范围内的
l=1;r=n+1;
//如果区间内有值
while(l<r)
{
mid=(l+r)/2;
if(a[mid]>x) r=mid;
if(a[mid]<x) l=mid+1;
if(a[mid]==x)
{
printf("%d\n",mid);
return 0;
}
}
printf("-1\n");
return 0;
}
关于mid的三种写法
- mid=(l+r)/2
- mid=(l+r)>>1
- mid=l+(r-l)/2
查找左边界
- 如果a[mid]==x 还要向左边继续查找 看左边是否还有x
- 找左边界的本质:找数组中第一个>=x的位置
- 找到l的下标之后,要判断a[l]==x(如果有负数,找0,要判断l是否还在数组的下标范围之内 否则会把找出数组范围的0当成要查找的0)
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+10;
int n,q,a[maxn],x,l,r,mid;
int find()
{
l = 1,r = n;
while(l<=r)
{
mid = l+r>>1;
//这个if可以和最后一个if合并起来写
if(a[mid]>x) r=mid-1;
if(a[mid]<x) l=mid+1;
//相等之后 还要继续往左边寻找
if(a[mid]==x) r=mid-1;
}
if(a[l]==x && l>=1 && l<=n) return l;
return -1;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
scanf("%d",&q);
while(q--)
{
scanf("%d",&x);
printf("%d ",find());
}
return 0;
}
查找右边界
例:https://oj.czos.cn/p/1895
思路和查找左边界类似 只不过讨论的是r而不是l
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+10;
int n,q,a[maxn],x,l,r,mid;
int find()
{
int l=1,r=n;
while(l<=r)
{
mid = l+r>>1;
if(x<a[mid]) r=mid-1;
if(x>a[mid]) l=mid+1;
if(x==a[mid]) l=mid+1;
}
if(a[r]==x && r>=1 && r<=n) return r;
return -1;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
scanf("%d",&q);
while(q--)
{
scanf("%d",&x);
cout<<find()<<" ";
}
return 0;
}
查找左右边界例题:https://oj.czos.cn/p/2078
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+10;
int n,q,a[maxn],x,l,r,mid;
int l_find()
{
l=1,r=n;
while(l<=r)
{
mid=l+r>>1;
if(x<a[mid]) r=mid-1;
if(x>a[mid]) l=mid+1;
if(x==a[mid]) r=mid-1;
}
if(l>=1 && l<=n && a[l]==x) return l;
return -1;
}
int r_find()
{
l=1,r=n;
while(l<=r)
{
mid=l+r>>1;
if(x<a[mid]) r=mid-1;
if(x>a[mid]) l=mid+1;
if(x==a[mid]) l=mid+1;
}
if(r>=1 && r<=n && a[r]==x) return r;
return -1;
}
int main()
{
scanf("%d %d",&n,&q);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
while(q--)
{
scanf("%d",&x);
printf("%d %d\n",l_find(),r_find());
}
return 0;
}
例题
在两组数据当中同时出现的数:https://oj.czos.cn/p/1898
思路:由于题目需要从小到大排序,所以我们的思路就是先将两组数据排序,然后依次进行二分即可
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+10;
int n,m,a[maxn],b[maxn],l,r,mid;
int find(int x)
{
l=1,r=n;
while(l<=r)
{
mid=l+r>>1;
if(x<a[mid]) r=mid-1;
if(x>a[mid]) l=mid+1;
if(x==a[mid]) return true;
}
return false;
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=m;i++) scanf("%d",&b[i]);
sort(a+1,a+n+1);
sort(b+1,b+m+1);
for(int i=1;i<=m;i++)
{
if(find(b[i]))
{
cout<<b[i]<<" ";
}
}
return 0;
}
大学估分方案:https://oj.czos.cn/p/1899
思路:讨论L,左边界的查找结果L返回的是左边第一个>=x的数 右边界的查找结果L返回的是左边第一个>x的数,并且无论是左边界还是右边界,找到L之后都需要往L的左边去看,才可以找到分差更小的
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+10;
int n,m,l,r,mid,ans=0,x;
int a[maxn];
int main()
{
scanf("%d %d",&m,&n);
for(int i=1;i<=m;i++) scanf("%d",&a[i]);
//二分之前需要排序
sort(a+1,a+m+1);
while(n--)
{
scanf("%d",&x);
//二分特判
if(x<=a[1]) ans+=a[1]-x;
else if(x>=a[m]) ans+=x-a[m];
else{
//二分查找左边界
l=1,r=m;
while(l<=r)
{
mid=l+r>>1;
if(x<=a[mid]) r=mid-1;
if(x>a[mid]) l=mid+1;
}
//已经找到了l
ans += min(a[l]-x,x-a[l-1]);
}
}
printf("%d",ans);
return 0;
}
小X算排名 https://oj.czos.cn/p/1542
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+10;
int n;
int a[maxn],b[maxn];
bool cmp(int x,int y)
{
return x>y;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
b[i] = a[i];
}
sort(a+1,a+n+1,cmp);
//二分查找
for(int i=1;i<=n;i++)
{
int * p = lower_bound(a+1,a+n+1,b[i],cmp);
printf("%d\n",p-a);
}
return 0;
}
最长上升子序列(LIS) https://oj.czos.cn/p/1893
思路:
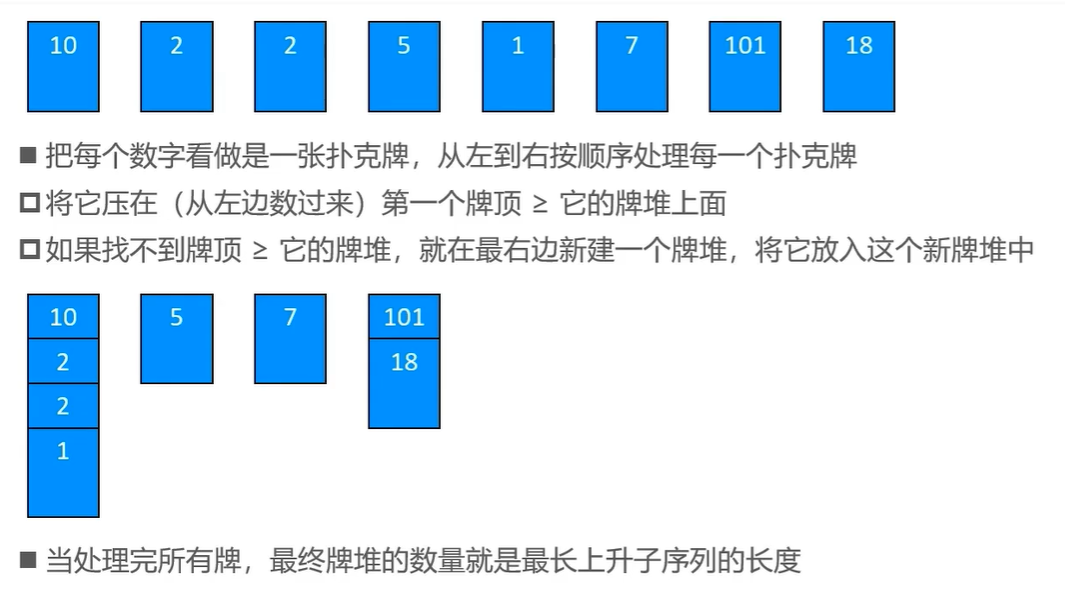
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+10;
int n,cnt;
int a[maxn],b[maxn];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
}
//二分搜索
b[++cnt] = a[1];
for(int i=2;i<=n;i++)
{
int p =lower_bound(b+1,b+cnt+1,a[i])-b;
//如果找到了
if(p!=cnt+1)
{
*lower_bound(b+1,b+cnt+1,a[i]) = a[i];
}else{
b[++cnt] = a[i];
}
}
printf("%d\n",cnt);
return 0;
}
最少的修改次数 https://oj.czos.cn/p/1902
思路:其实不难发现,要求最少的修改次数,其实就要先求出最长上升子序列,并且需要修改的个数其实就是总个数减去最长上升子序列的长度
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+10;
int n,cnt;
int a[maxn],b[maxn];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
}
//LIS
b[++cnt] = a[1];
for(int i=2;i<=n;i++)
{
//找牌顶
int p = lower_bound(b+1,b+cnt+1,a[i])-b;
//如果找到了 替换
if(p!=cnt+1)
{
*lower_bound(b+1,b+cnt+1,a[i]) = a[i];
}else{
b[++cnt] = a[i]; //没找到 放入牌中
}
}
printf("%d\n",n-cnt);
return 0;
}
二分答案
二分答案,指的是对于某些特定的问题,其答案往往具有单调性,分布在一个单调的区间内,我们可以通过使用二分算法来更快得到答案。
二分答案经常用来处理最值中的最值问题
伐木工 https://oj.czos.cn/p/1908
对于高度为mid,可以得到>=m的木材,那么我们就可以继续升高mid,所以我们应该二分的是右边界
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6+10;
long long a[maxn],n,m,l=1,r=INT_MIN,mid;
bool check()
{
long long s = 0;
for(int i=1;i<=n;i++)
{
if(mid<a[i]) s+=a[i]-mid;
if(s>=m) return true;
}
return false;
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
r=max(r,a[i]);
}
//二分答案 右边界
while(l<=r)
{
mid = l+r>>1;
if(check()) l=mid+1;
else r=mid-1;
}
printf("%d\n",r);
return 0;
}
防御迷阵 https://oj.czos.cn/p/1916
思路:对于本题的数据范围而言,如果使用DFS回溯搜索路径的话,那么会超过时间复杂度限制,因为伤害值的范围在一个a[min,max]的范围内单调递增,所以我们可以考虑二分伤害最小值,然后利用广搜,从1,1点出发,如果能够走到迷阵最后一行,那么该答案可行,继续二分更小的结果,本质就是二分左边界
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e3+10;
int n,m,l=INT_MAX,r=INT_MIN,mid,head,tail;
int a[maxn][maxn],q[1000100][3],vis[maxn][maxn];
int dx[5] = {0,0,1,0,-1};
int dy[5] = {0,1,0,-1,0};
bool check(int v)
{
//初始化
memset(vis,false,sizeof(vis));
q[1][1] = 1;
q[1][2] = 1;
vis[1][1] = true;
head=1,tail=1;
int tx,ty;
//bfs广搜
while(head<=tail)
{
for(int i=1;i<=4;i++)
{
tx=q[head][1]+dx[i];
ty=q[head][2]+dy[i];
if(tx>=1&&tx<=n&&ty>=1&&ty<=m&&!vis[tx][ty]&&a[tx][ty]<=v)
{
tail++;
q[tail][1] = tx;
q[tail][2] = ty;
vis[tx][ty] = true;
if(tx==n)
{
return true;
}
}
}
head++;
}
return false;
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
scanf("%d",&a[i][j]);
if(i!=1 && i!=n)
{
l=min(l,a[i][j]);
r=max(r,a[i][j]);
}
}
}
//二分答案
while(l<=r)
{
mid=l+r>>1;
if(check(mid)) r=mid-1;
else l=mid+1;
}
//左边界
printf("%d\n",l);
return 0;
}
跳石头 https://oj.czos.cn/p/1909
思路:
二分答案:要求的是最小跳跃距离的最大值
边界:右边界
二分对象:最小跳跃距离 范围[1,l]
check函数:检查跳跃距离为mid的时候,需要搬走的
石块的数量c
- 如果c<=m的话,l=mid+1
- 如果c>m的话,r=mid-1
#include <iostream>
using namespace std;
const int N = 5e4+10;
int l,n,m,L,R,mid;
int a[N];
bool check(int v)
{
//判断最小距离为v的时候 能够搬走的石头的数量
int c = 0; //搬走的数量
int p = 0; //人的位置
for(int i=1;i<=n;i++)
{
if(a[i]-p<v)
{
c++;
}else{
p=a[i];
}
}
//特判 最后一块石头搬走之后c的值与m的关系
if(l-p<v) c++;
return c<=m; //返回结果
}
int main()
{
scanf("%d %d %d",&l,&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
//二分右边界
L=1,R=l;
while(L<=R)
{
mid=L+R>>1;
if(check(mid)) L=mid+1;
else R=mid-1;
}
printf("%d\n",R);
return 0;
}
进击的奶牛 https://oj.czos.cn/p/1910
思路:
二分对象:最近距离[1,max]
求最大值 右边界
对于一个最近距离mid
check(mid)函数:
对于一个最近距离mid 判断是否能够安排c头牛
判断能否满足 将数组排序之后
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
int n,c,l,r=INT_MIN,mid;
int a[N];
bool check(int v)
{
int p = 0;//表示当前牛的位置
int tot = 0;//表示安排了多少只牛
//初始化
p = a[1];
tot = 1;
//安排
for(int i=2;i<=n;i++)
{
//实时更新牛的位置
if(a[i]-p>=v) p=a[i],tot++;
}
//返回结果
return tot>=c;
}
int main()
{
scanf("%d %d",&n,&c);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
r=max(r,a[i]);
}
sort(a+1,a+n+1);
//二分答案
l=1;
while(l<=r)
{
mid=l+r>>1;
if(check(mid)) l=mid+1;
else r=mid-1;
}
printf("%d\n",r);
return 0;
}
最小的空旷指数 https://oj.czos.cn/p/1912
思路:
二分答案
二分对象:相邻路标的最大距离
二分范围:[1,n]
求最小值 左边界
分析check(mid)函数:
对于一个最大距离mid 如果出现两个路标之间的距离比mid还大 分割它们(即安排路标)
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
int l,n,k,L,R,mid;
int a[N];
/*
*/
bool check(int v)
{
int c=0;//安排的路标数量
//安排路标
for(int i=2;i<=n;i++)
{
if(a[i]-a[i-1]>=v)
{
c+=(a[i]-a[i-1])/v;
if((a[i]-a[i-1])%v==0)
{
c--;
}
}
}
//返回结果
return c<=k;
}
int main()
{
scanf("%d %d %d",&l,&n,&k);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
sort(a+1,a+n+1);
L=1,R=l;
while(L<=R)
{
mid=L+R>>1;
if(check(mid)) R=mid-1;
else L=mid+1;
}
printf("%d",L);
return 0;
}
买木头 https://oj.czos.cn/p/1561
二分答案 寻找右边界
二分对象:最长木头长度 范围是[1,max]
check(mid) 对于木头长度为mid 计算木头数量c 如果c>=m 继续二分
#include <bits/stdc++.h>
using namespace std;
const int N = 1e4+10;
int n,m,L,R,mid;
int l[N];
int s[N];
//检查长度为v时能否得到m根木头
bool check(int v)
{
int c = 0;
for(int i=1;i<=n;i++) c+=(l[i]/v)*s[i];
return c>=m;
}
int main()
{
//生成数据
scanf("%d %d %d %d",&n,&m,&l[1],&s[1]);
R=l[1];
for(int i=2;i<=n;i++)
{
l[i] = ((l[i-1]*37011+10193)%10000)+1;
s[i] = ((s[i-1]*73011+24793)%100)+1;
R=max(R,l[i]);
}
//二分
L=1;
while(L<=R)
{
mid=L+R>>1;
if(check(mid)) L=mid+1;
else R=mid-1;
}
printf("%d\n",R);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号