从数学概念到图像识别，再到 CNN 的联系

在矩阵论和信号处理中，奇异值分解（Singular Value Decomposition, SVD） 是一个极其重要的工具。它不仅是一个数学分解公式，更是连接数据压缩、特征提取和深度学习优化的桥梁 。

矩阵与奇异值的定义

  • 对任意矩阵 \(A \in \mathbb{R}^{m \times n}\)，其奇异值分解为：

    \[A = U\,\Sigma\,V^{\mathsf T} \]

  • 其中：
    • \(U \in \mathbb{R}^{m \times m}\)：左奇异向量矩阵（正交基，描述输出方向）；
    • \(\Sigma \in \mathbb{R}^{m \times n}\)：奇异值对角矩阵（非负实数，按大小排序）；
    • \(V \in \mathbb{R}^{n \times n}\)：右奇异向量矩阵（正交基，描述输入方向）。

奇异值的物理/几何意义

  • 几何解释：矩阵 \(A\) 作用在单位圆（球）上，会把它拉伸成椭圆（椭球）。椭圆的长短轴长度就是奇异值 \(\sigma_1,\sigma_2,\dots\)，轴的方向由 \(U, V\) 决定。
  • 能量解释：奇异值的平方 \(\sigma_i^2\) 表示对应模态（方向）的能量贡献。
  • 工程意义：奇异值按从大到小排序，体现矩阵的重要模式——大的对应主体结构，小的多为细节或噪声。

我们可以借助代码理解对描述图像的张量进行解释，看看图像是如何被压缩的。

import os, glob, math
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
import pandas as pd

# ========== 1) 查找当前目录中的苹果图片 ==========
def find_apple_image():
  patterns = [
      "apple.*", "Apple.*", "*apple*.*", "*Apple*.*",
      "apples.*", "*apples*.*"
  ]
  exts = (".png", ".jpg", ".jpeg", ".bmp", ".tif", ".tiff", ".webp")

  candidates = []
  for pat in patterns:
      candidates += glob.glob(pat)
  candidates = [p for p in candidates if os.path.splitext(p)[1].lower() in exts]

  if not candidates:
      candidates = [p for p in os.listdir(".") if os.path.splitext(p)[1].lower() in exts]
  if not candidates:
      raise FileNotFoundError("No image file found in current directory. "
                              "Place an apple image here or pass image_path manually.")
  candidates.sort(key=lambda x: (len(x), x))
  return candidates[0]

# ========== 2) 读为灰度矩阵 ==========
def load_gray_image(image_path):
  img = Image.open(image_path).convert("L")      # 灰度
  A = np.asarray(img, dtype=np.float64)          # 0..255
  return A, img

# ========== 3) SVD 与重建 ==========
def svd_decompose(A):
  U, s, Vt = np.linalg.svd(A, full_matrices=False)  # A = U @ diag(s) @ Vt
  return U, s, Vt

def reconstruct_topk(U, s, Vt, k):
  k = max(1, min(k, len(s)))
  Ak = (U[:, :k] * s[:k]) @ Vt[:k, :]
  return np.clip(Ak, 0, 255)

# ========== 4) 指标 ==========
def compression_ratio(m, n, k):
  # 原 ~ m*n；SVD top-k ~ k*(m + n + 1)
  return (m * n) / (k * (m + n + 1))

def mse(a, b):
  return float(np.mean((a - b) ** 2))

# ========== 5) 小尺寸网格展示（1 行或 2 行） ==========
def show_comparisons(A, reconstructions, k_values, rows=1, dpi=150):
  """
  rows: 1 或 2（推荐 1 行或 2 行展示）
  dpi: 控制整体清晰度（配合 figsize）
  """
  panels = [(A, "Original")] + list(zip(reconstructions, [f"K={k}" for k in k_values]))
  total = len(panels)
  rows = 1 if rows <= 1 else 2
  cols = math.ceil(total / rows)

  # 每个小图 2.6~3.0 英寸宽比较紧凑
  fig, axes = plt.subplots(rows, cols, figsize=(2.8*cols, 2.8*rows), dpi=dpi)
  if rows == 1:
      axes = np.array(axes).reshape(1, -1)
  axes_flat = axes.ravel()

  for i, (img, title) in enumerate(panels):
      ax = axes_flat[i]
      ax.imshow(img, cmap="gray", vmin=0, vmax=255)
      ax.set_title(title, fontsize=10)
      ax.axis("off")

  # 多余的子图隐藏
  for j in range(len(panels), len(axes_flat)):
      axes_flat[j].axis("off")

  plt.tight_layout()
  plt.show()

# ========== 6) 主流程 ==========
def svd_compress_compare(
  image_path=None,
  k_values=(5, 10, 20, 50, 100),
  save_prefix="svd_apple",
  grid_rows=1    # 改成 2 即两行展示
):
  if image_path is None:
      image_path = find_apple_image()
  print(f"[INFO] Using image: {image_path}")

  A, _ = load_gray_image(image_path)
  m, n = A.shape
  print(f"[INFO] Image shape: {m}x{n}")

  U, s, Vt = svd_decompose(A)

  # 保存奇异值与左右系数（便于复查）
  top = min(50, len(s))
  pd.DataFrame({"index": np.arange(1, top+1), "sigma": s[:top]}).to_csv(
      f"{save_prefix}_sigma_top{top}.csv", index=False
  )
  pd.DataFrame(U[:, :10]).to_csv(
      f"{save_prefix}_U_first10_cols.csv", index=False,
      header=[f"u{i+1}" for i in range(min(10, U.shape[1]))]
  )
  pd.DataFrame(Vt[:10, :]).to_csv(
      f"{save_prefix}_Vt_first10_rows.csv", index=False,
      header=[f"v_coord{j+1}" for j in range(Vt.shape[1])]
  )

  # 奇异值衰减曲线
  plt.figure(figsize=(6,4))
  plt.semilogy(s[:min(200, len(s))])
  plt.title("Singular Value Decay")
  plt.xlabel("Index")
  plt.ylabel("Sigma (log scale)")
  plt.tight_layout()
  plt.savefig(f"{save_prefix}_sigma_decay.png", dpi=150)
  plt.show()

  # 原图保存
  Image.fromarray(A.astype(np.uint8)).save(f"{save_prefix}_original.png")

  # 重建
  reconstructions = []
  rows_table = []
  for k in k_values:
      Ak = reconstruct_topk(U, s, Vt, k)
      reconstructions.append(Ak)
      cr = compression_ratio(m, n, k)
      e  = mse(A, Ak)
      out_path = f"{save_prefix}_k{k}.png"
      Image.fromarray(Ak.astype(np.uint8)).save(out_path)
      rows_table.append({"K": k, "Compression_Ratio(≈)": f"{cr:.1f}:1", "MSE": e, "Output": out_path})

  # 控制在一行或两行展示
  show_comparisons(A, reconstructions, k_values, rows=grid_rows, dpi=150)

  # 控制台指标总结
  df = pd.DataFrame(rows_table)
  print("\n=== Compression Comparison ===")
  print(df.to_string(index=False))

  # Rank-1 组件可视化（对比看主成分结构）
  rank1 = np.outer(U[:, 0], Vt[0, :]) * s[0]
  mn, mx = rank1.min(), rank1.max()
  rank1_vis = (rank1 - mn) / (mx - mn + 1e-12) * 255
  Image.fromarray(rank1_vis.astype(np.uint8)).save(f"{save_prefix}_rank1_component_vis.png")

  print("\nFiles saved:")
  print(f" - {save_prefix}_original.png")
  print(f" - {save_prefix}_sigma_decay.png")
  for r in rows_table:
      print(f" - {r['Output']}")
  print(f" - {save_prefix}_sigma_top{top}.csv")
  print(f" - {save_prefix}_U_first10_cols.csv (left factors)")
  print(f" - {save_prefix}_Vt_first10_rows.csv (right factors)")
  print(f" - {save_prefix}_rank1_component_vis.png (visualized σ1·u1·v1ᵀ)")

# ========== 运行 ==========
if __name__ == "__main__":
  svd_compress_compare(k_values=[5, 10, 20, 50, 100], grid_rows=1)

通过代码把一张苹果的图片读取成向量然后把这个彩色的图片只保留了灰色的通道，通过U, s, Vt = np.linalg.svd(A, full_matrices=False) 读取图片数据的奇异值，然后画图查看这个奇异值变化的规则
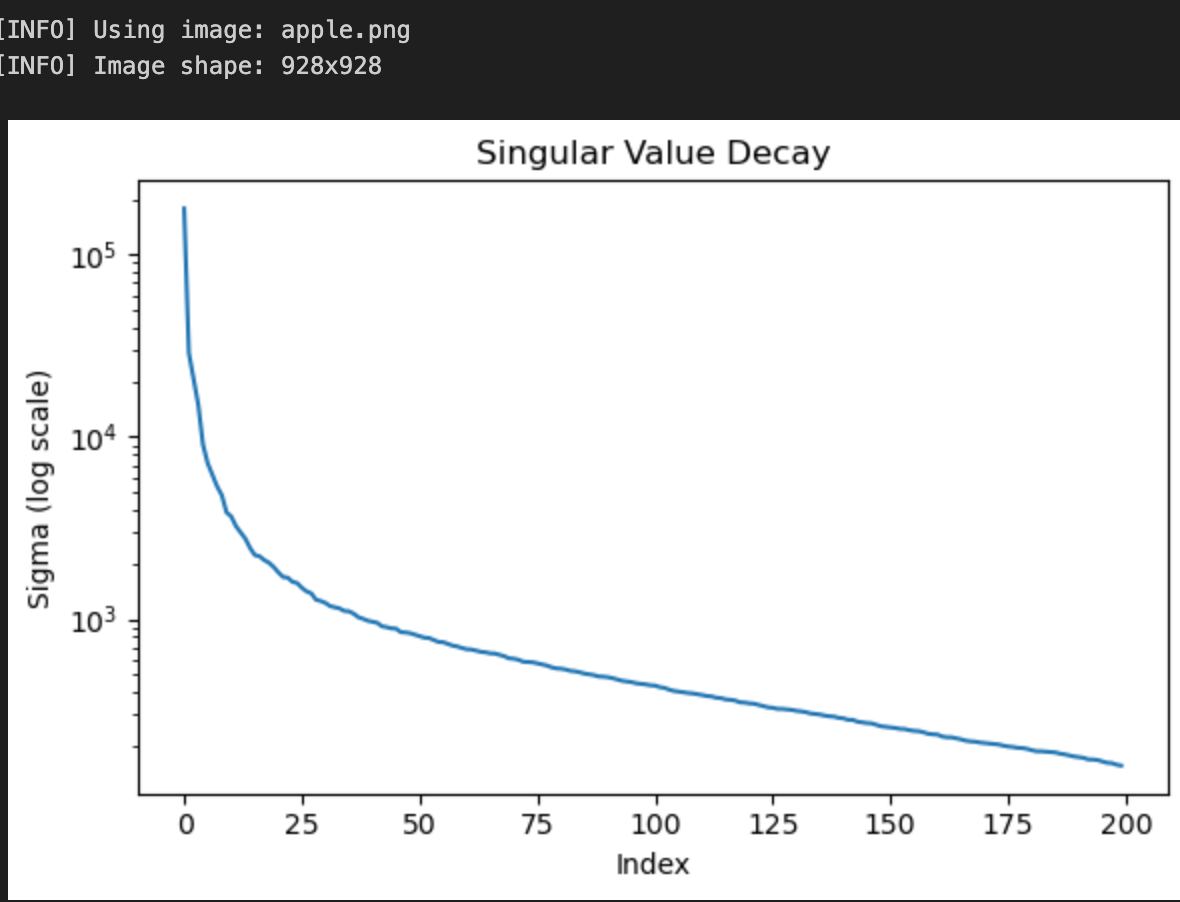
image
随着我们对奇异值 k_values=(5, 10, 20, 50, 100) 取前五 10 和 500 和100 保持其余的左右系数不变，可以画图查看图盘分辨率的变化
image

奇异值在 CNN 训练中与 BN 的关联

1) 没有 BN 时：奇异值带来的两类问题

(a) 前向激活的幅度失衡（Internal Covariate Shift）

设一层的线性变换为 \(z = W x + b\)。若权重矩阵 \(W\) 的谱分布很“尖锐”（少数奇异值 \(\sigma_i\) 很大，其余很小），则有

\[\|z\| \approx \|W\|_2 \cdot \|x\| \]

即沿最大奇异向量的方向被强放大，导致部分通道/方向的激活方差远大于其它方向，分布漂移严重，使 ReLU/SiLU 等非线性层的工作区间失衡。

(b) 反向传播的梯度爆炸/消失（Jacobian 条件数）

该层的雅可比为

\[J = \frac{\partial z}{\partial x} = W, \]

其条件数

\[\kappa(W) = \frac{\sigma_{\max}(W)}{\sigma_{\min}(W)} \]

若很大，则为病态：梯度沿大奇异向量方向被放大、沿小奇异向量方向衰减；跨层相乘后，梯度范数极不稳定（爆炸或消失）。

2) BN 做了什么：把“非线性之前”的尺度标准化

(a) 消去线性尺度（对 \(W\) 的“尺度不变性”）

若将权重等比例缩放为 \(cW\)：

\[z' = cW x + b, \]

经过 BN：

\[\hat z' = \frac{z' - \mu'}{\sqrt{(\sigma')^2 + \varepsilon}} \approx \hat z, \]

即均值/方差的缩放被抵消。
结论： BN 使网络对权重的整体缩放近似不敏感（scale-invariant），把“有效谱尺度”的可调性交给可学习参数 \(\gamma\)。

(b) 统一每个通道的方差（归一化激活能量）

BN 使每个通道满足

\[\mathrm{Var}[\hat z_j] \approx 1, \]

将前向能量在通道上“拉平”，避免“某些方向能量过强、另一些方向几乎没有”的极端现象。

3) 从奇异值视角看 BN 的效果

  1. 压制 \(\sigma_{\max}(W)\) 的直接影响
    即使 \(W\) 的最大奇异值很大，BN 将进入非线性前的尺度拉回到可控范围。

  2. 改善层雅可比的条件数
    在统计意义上让不同通道方差接近，使雅可比谱分布更集中，减少梯度爆炸/消失的连乘效应。

  3. 把“谱尺度调节”交给 \(\gamma\)
    训练中 \(\gamma\) 学习“哪些方向需要更大有效增益”，等价于在归一化的底座上进行受控的方向性放大。

直观比喻： BN 先把“地面找平”（统一方差），再由 \(\gamma\) 在需要的位置“加台阶”；比在凹凸不平的地面上修台阶（无 BN）更稳定。

4) 对训练动力学的具体好处（用奇异值语言）

  • 更稳定的学习率： 对 \(W\) 的等比例缩放不敏感，参数范数变化不再直接导致前向/反向幅度的剧烈波动，允许更大的全局学习率。
  • 优化景观更平滑： 归一化降低了损失对尺度方向的敏感性，缓解“尖锐极小值/病态峡谷”，收敛更快。
  • 跨层梯度范数可控： 层雅可奇异值集中在较窄区间，避免层间相乘引发的指数级爆炸/衰减。

奇异值： 大/小奇异值的不均衡会放大训练的不稳定；BN 的核心贡献是标准化非线性前的尺度，使“有效雅可比”的谱更集中，再由可学习的 \(\gamma\) 做精细放大，从而获得稳定梯度与更快收敛。

posted @ 2025-10-19 15:20  方子敬  阅读(16)  评论(0)    收藏  举报