感知机与线性分类器（线性模型的起点）

1：感知机本质上是一个线性二分类器。
\(y = f(w^{\mathsf{T}} x + b)\)

其中：
• x：输入向量（例如图像拉直后的像素向量）
• w：权重向量
• b：偏置项
激活函数：

\[f(z)= \begin{cases} +1, & z \ge 0 \\ -1, & z < 0 \end{cases} \]

线性判别式：

\[y = f(\mathbf{w}^{\mathsf{T}}\mathbf{x} + b) \]

换句话说，感知机就是用一条“直线”（二维）、“平面”（三维）、或“超平面”（高维）来划分不同类别。

⸻

学习规则（Rosenblatt）：

\[\begin{aligned} \mathbf{w} &\leftarrow \mathbf{w} + \eta\,(y_{\text{true}} - y_{\text{pred}})\,\mathbf{x} \\ b &\leftarrow b + \eta\,(y_{\text{true}} - y_{\text{pred}}) \end{aligned} \]

\[\mathbf{w} \leftarrow \mathbf{w} + \eta\,y_{\text{true}}\,\mathbf{x},\qquad b \leftarrow b + \eta\,y_{\text{true}} \quad\text{(当且仅当误分类时)} \]

核心思想：
• 预测正确 → 不更新
• 预测错误 → 推动 w, b，让边界往正确方向移动

⸻

4. 代码实验

我们通过一个二维点的例子来演示感知机如何学会分类。

import numpy as np
import matplotlib.pyplot as plt

# 数据：二维点
X = np.array([[2,3],[4,5],[3,3],[1,-1],[2,-2],[3,-1]])
y = np.array([1,1,1,-1,-1,-1])  # 标签

# 初始化参数
w = np.zeros(2)
b = 0
eta = 0.1  # 学习率

# 训练
for epoch in range(20):
    for i in range(len(X)):
        x_i, y_true = X[i], y[i]
        y_pred = 1 if np.dot(w, x_i) + b >= 0 else -1
        if y_true != y_pred:
            w += eta * y_true * x_i
            b += eta * y_true

print("训练后的权重:", w)
print("训练后的偏置:", b)

# 可视化
x1 = np.linspace(-3, 6, 100)
x2 = -(w[0]*x1 + b) / w[1]

plt.scatter(X[y==1][:,0], X[y==1][:,1], color='blue', marker='o', label='Class A')
plt.scatter(X[y==-1][:,0], X[y==-1][:,1], color='red', marker='x', label='Class B')
plt.plot(x1, x2, 'k-')
plt.legend()
plt.title("感知机分类边界")
plt.show()

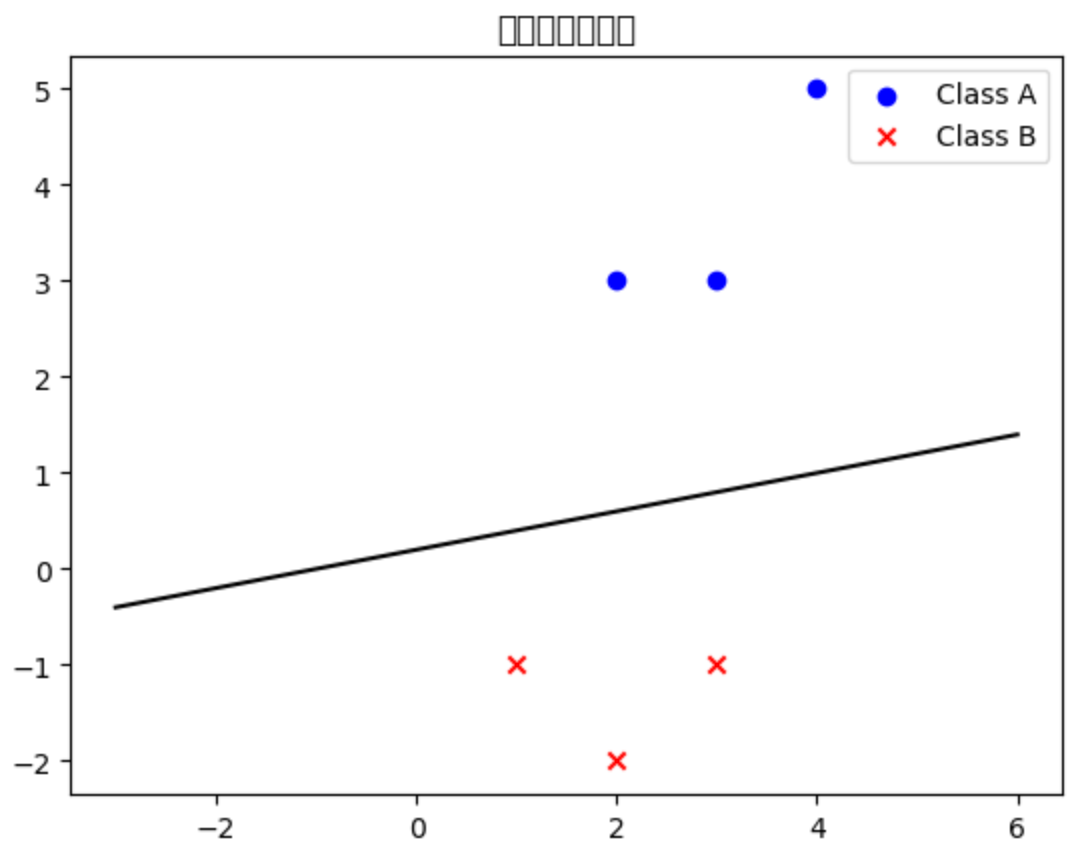
运行结果：
• 蓝色圆点：类别 A
• 红色叉号：类别 B
• 黑色直线：感知机学到的分类边界

⸻

小结
• 感知机的本质：通过一个超平面分割数据。
• 学习规则：仅在预测错误时调整参数。
• 高维推广：从二维直线到三维平面，再到高维超平面。
• 核心思想：通过权重和偏置的学习，我们逐渐逼近数据的特征表达，得到可以区分类别的决策函数。