【第17期Datawhale | 零基础入门金融风控-贷款违约预测】Task01打卡：赛题理解、常见分类指标评价计算示例

零基础入门金融风控-贷款违约预测 Task01

参赛链接 https://tianchi.aliyun.com/competition/entrance/531830/information

Task01 赛题理解

md

零基础入门金融风控-贷款违约预测

目的: 根据贷款申请人的数据信息预测其是否有违约的可能，以此判断是否通过此项贷款，这是一个典型的分类问题

导包

import os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import datetime

公共变量

file_path = 'E:\\阿里云开发者-天池比赛\\02_零基础入门金融风控_贷款违约预测\\'
train_file_path = file_path+'train.csv'
testA_file_path = file_path+'testA.csv'
now = datetime.datetime.now().strftime('%Y-%m-%d_%H:%M:%S')

#%% 1.6.1 数据读取pandas

train = pd.read_csv(train_file_path)
testA = pd.read_csv(testA_file_path)
print('Train Data shape 行*列:',train.shape)
print('TestA Data shape 行*列:',testA.shape)
print('train 所有列: \n', train.columns.values)
print('testA 所有列: \n', testA.columns.values)
print('结果列  isDefault'
      'testA相较于train多出两列: \'n2.2\' \'n2.3\' ')

输出

Train Data shape 行列: (800000, 47)
TestA Data shape 行列: (200000, 48)
train 所有列:

 ['id' 'loanAmnt' 'term' 'interestRate' 'installment' 'grade' 'subGrade' 'employmentTitle' 'employmentLength' 'homeOwnership' 'annualIncome'
 'verificationStatus' 'issueDate' 'isDefault' 'purpose' 'postCode' 'regionCode' 'dti' 'delinquency_2years' 'ficoRangeLow' 'ficoRangeHigh'
 'openAcc' 'pubRec' 'pubRecBankruptcies' 'revolBal' 'revolUtil' 'totalAcc' 'initialListStatus' 'applicationType' 'earliesCreditLine' 'title'
 'policyCode' 'n0' 'n1' 'n2' 'n2.1' 'n4' 'n5' 'n6' 'n7' 'n8' 'n9' 'n10' 'n11' 'n12' 'n13' 'n14']

testA 所有列:

 ['id' 'loanAmnt' 'term' 'interestRate' 'installment' 'grade' 'subGrade' 'employmentTitle' 'employmentLength' 'homeOwnership' 'annualIncome'
 'verificationStatus' 'issueDate' 'purpose' 'postCode' 'regionCode' 'dti' 'delinquency_2years' 'ficoRangeLow' 'ficoRangeHigh' 'openAcc' 'pubRec'
 'pubRecBankruptcies' 'revolBal' 'revolUtil' 'totalAcc' 'initialListStatus' 'applicationType' 'earliesCreditLine' 'title'
 'policyCode' 'n0' 'n1' 'n2' 'n2.1' 'n2.2' 'n2.3' 'n4' 'n5' 'n6' 'n7' 'n8' 'n9' 'n10' 'n11' 'n12' 'n13' 'n14']

易得

结果列 isDefault， testA 相较于train多出两列: 'n2.2' 'n2.3'

---

分类指标评价计算示例

混淆矩阵: 精度评价的一种标准格式，用n行n列的矩阵形式来表示实际:预测的映射数目

import numpy as np
from sklearn.metrics import confusion_matrix
y_true = [0, 1, 2, 0] # 真实值
y_pred = [0, 1, 0, 1] # 预测值
print('混淆矩阵:(1真,0假),每一行代表了数据的真实归属类别,每一列代表了预测类别,矩阵中的大小代表出现次数个数\n',
      confusion_matrix(y_true, y_pred))

输出

混淆矩阵:(1真,0假)
 [[1 1 0]
 [0 1 0]
 [1 0 0]]

accuracy 准确率

from sklearn.metrics import accuracy_score
y_pred = [0, 1, 1, 1]
y_true = [0, 1, 1, 0]
print('ACC:',accuracy_score(y_true, y_pred))

输出

ACC: 0.75

Precision,Recall,F1-score

from sklearn import metrics
y_pred = [0, 1, 1, 1]
y_true = [0, 1, 1, 0]
#（1）若一个实例是正类，并且被预测为正类，即为真正类TP(True Positive )
#（2）若一个实例是正类，但是被预测为负类，即为假负类FN(False Negative )
#（3）若一个实例是负类，但是被预测为正类，即为假正类FP(False Positive )
#（4）若一个实例是负类，并且被预测为负类，即为真负类TN(True Negative )
print('Precision 精确率，正确预测为正样本（TP）占预测为正样本(TP+FP)的百分比:\n',metrics.precision_score(y_true, y_pred))
print('Recall 召回率、查全率, 预测为正样本(TP)的数目占真实的正样本(TP+FN)的百分比\n',metrics.recall_score(y_true, y_pred))
print('F1-score 兼顾上述两者= 1/（1/Precision + 1/Recall）:\n',metrics.f1_score(y_true, y_pred))

输出

Precision 精确率，正确预测为正样本（TP）占预测为正样本(TP+FP)的百分比:
 0.6666666666666666
Recall 召回率、查全率, 预测为正样本(TP)的数目占真实的正样本(TP+FN)的百分比
 1.0
F1-score 兼顾上述两者= 1/（1/Precision + 1/Recall）:
 0.8

P-R曲线

import matplotlib.pyplot as plt
from sklearn.metrics import precision_recall_curve
y_pred = [0, 1, 1, 0, 1, 1, 0, 1, 1, 1]
y_true = [0, 1, 1, 0, 1, 0, 1, 1, 0, 1]
precision, recall, thresholds = precision_recall_curve(y_true, y_pred)
# 以下绘图
plt.rcParams['font.sans-serif'] = ['SimHei']  # 显示中文标签
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(8, 4))
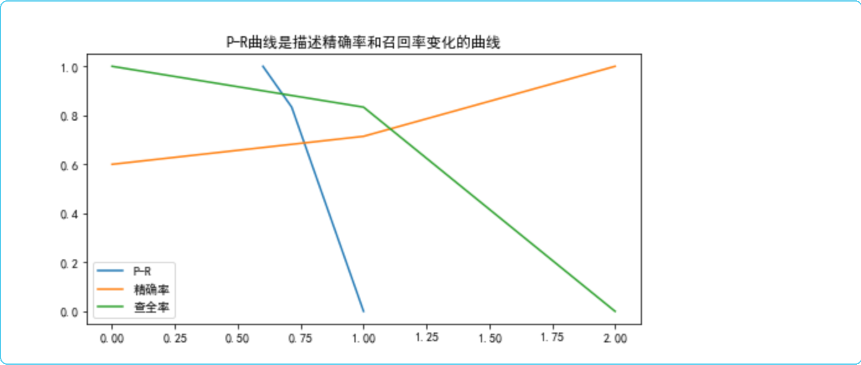
plt.title('P-R曲线是描述精确率和召回率变化的曲线')
plt.plot(precision, recall, label='P-R')
plt.plot(precision,label='精确率')
plt.plot(recall, label='查全率')
plt.legend(loc='best')
plt.show()

输出

ROC曲线

"""
ROC（Receiver Operating Characteristic）
1. ROC空间将假正例率（FPR）定义为 X 轴，真正例率（TPR）定义为 Y 轴。
TPR：在所有实际为正例的样本中，被正确地判断为正例之比率。
FPR：在所有实际为负例的样本中，被错误地判断为正例之比率。
"""
from sklearn.metrics import roc_curve
y_pred = [0, 1, 1, 0, 1, 1, 0, 1, 1, 1]
y_true = [0, 1, 1, 0, 1, 0, 1, 1, 0, 1]
FPR,TPR,thresholds=roc_curve(y_true, y_pred)
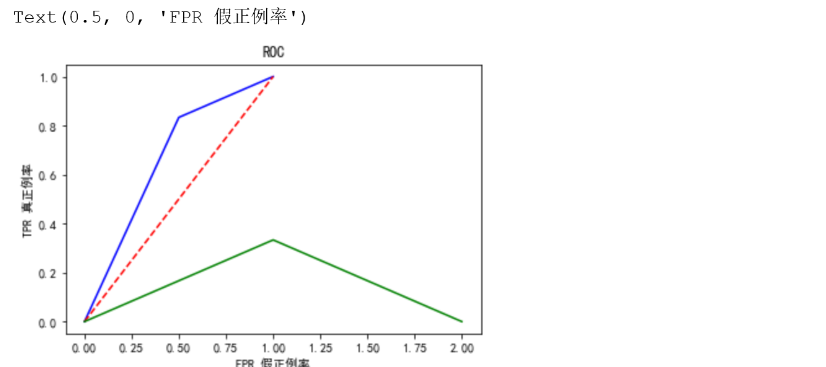
plt.title('ROC')
plt.plot(FPR, TPR,'b')
plt.plot([0,1],[0,1],'r--')
plt.plot(abs(FPR-TPR),'g--')
plt.ylabel('TPR 真正例率')
plt.xlabel('FPR 假正例率')

输出

AUC : ROC曲线下面积

"""
AUC（Area Under Curve）被定义为 ROC曲线 下与坐标轴围成的面积，显然这个面积的数值不会大于1。
又由于ROC曲线一般都处于y=x这条直线的上方，所以AUC的取值范围在0.5和1之间。
AUC越接近1.0，检测方法真实性越高;等于0.5时，则真实性最低，无应用价值
"""
from sklearn.metrics import roc_auc_score
y_true = np.array([0, 0, 1, 1])
y_scores = np.array([0.1, 0.4, 0.35, 0.8])
print('AUC socre:',roc_auc_score(y_true, y_scores))

输出

AUC socre: 0.75

金融风控预测类常见的评估指标 之K-S曲线

"""
 K-S曲线将真正例率和假正例率都作为纵轴，横轴则由选定的阈值来充当。
公式如下：
KS = abs(FPR-TPR).max()
KS不同代表的不同情况，一般情况KS值越大，模型的区分能力越强，但是也不是越大模型效果就越好，如果
KS过大，模型可能存在异常，所以当KS值过高可能需要检查模型是否过拟合。以下为KS值对应的模型情况，
但此对应不是唯一的，只代表大致趋势。
3. KS值<0.2,一般认为模型没有区分能力。
4. KS值[0.2,0.3],模型具有一定区分能力，勉强可以接受
5. KS值[0.3,0.5],模型具有较强的区分能力。<<<<<<<<<<<<<<<<<<
6. KS值大于0.75，往往表示模型有异常。
"""

KS值 在实际操作时往往使用ROC曲线配合求出KS值 实现简易函数

KS=abs(FPR-TPR).max()
# 实现简易函数
print('KS值：',KS)
if KS<0.2:
    print(' KS<0.2 一般认为模型没有区分能力。')
elif KS >= 0.2 and KS <=0.3:
    print(' KS值[0.2,0.3],模型具有一定区分能力，勉强可以接受')
elif KS >= 0.3 and KS <=0.5:
    print(' KS值[0.3,0.5],模型具有较强的区分能力。<<<<<<<<<<<<<<<<<<')
elif KS >= 0.5 and KS <=0.75:
    print(' KS值[0.5,0.75]，模型介于较强的区分能力或者异常之间')
else:
    print(' KS值大于0.75，往往表示模型有异常。')

输出

KS值： 0.33333333333333337
KS值[0.3,0.5],模型具有较强的区分能力。<<<<<<<<<<<<<<<<<<