2127D-Root was Built by Love, Broken by Destiny

题目

Heartfall河横贯Destinyland，将其分为南北两岸。

工程师Root想沿河建造\(n\)栋房子，编号从1到\(n\)。所有北岸的房子和所有南岸的房子必须沿与Heartfall河平行的直线排列。

共有\(m\)座桥，第\(i\)座桥连接房子\(u_i\)和房子\(v_i\)（\(u_i \ne v_i\)）。保证所有\(n\)栋房子都通过这些桥相连，即，可以通过桥从任意一栋房子到达另一栋房子。另外，没有两座桥连接同一对房子。

Root想知道，有多少种方式能沿河排列这\(n\)栋房子（对结果取模\(10^9 + 7\)），使得对于计划中的\(m\)座桥满足以下条件：

• 每座桥连接的两栋房子分别位于河的两岸；
• 当桥被画为连接房子的直线时，这些桥不会相互交叉。
  

（图片说明：当\(n=5\)时房子的一种可能排列）

两种排列如果满足以下至少一条，则视为不同：

• 有一栋房子在两种排列中位于不同的河岸；
• 存在两栋房子\(a\)和\(b\)，它们在两种排列中位于同一河岸，但在一种排列中\(a\)排在\(b\)前面，而另一种排列中\(b\)排在\(a\)前面。

由于Root被他的前任分心（命运将他们分开），他请求你计算沿河排列房子的方式数，对结果取模\(10^9 + 7\)。

思路

首先判断怎样的图是合法的

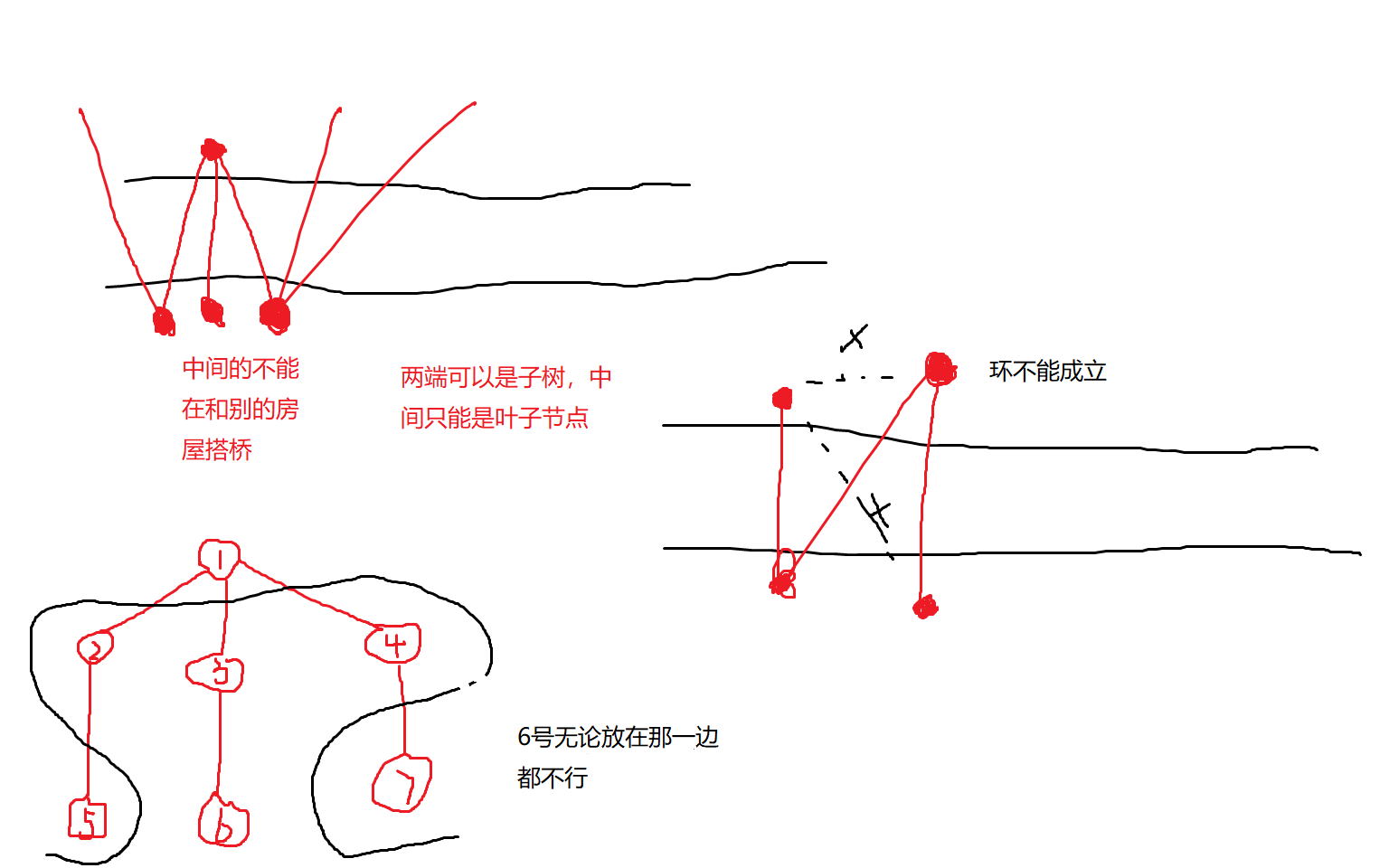
• 图必须是无环的，如果有环，那么必然会有桥搭在陆地上或者两座桥相交
  
• 同时，我们可以发现跟一个节点\(u\)相连的节点\(v_i\),都在节点\(u\)的对面，而只有在最外端的两个节点可以连别的点，中间只能是叶子节点，否则就会产生交叉

\[所以，可以得出结论，如果一个图没有环，并且每个点的非叶子节点最多只有两个，那么它是合法的 \]

如何计数

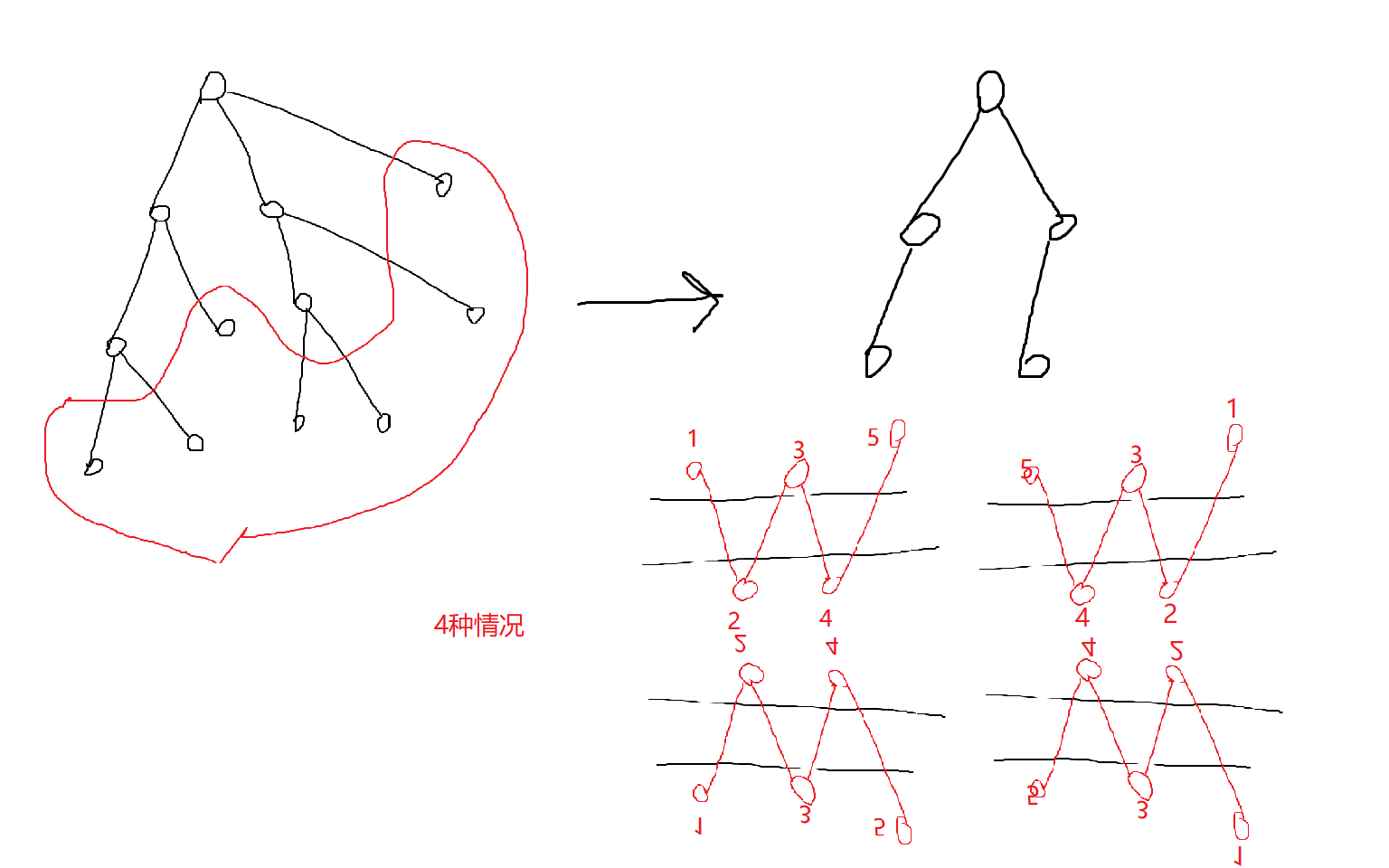
• 我们可以先把叶子节点去掉，（因为这样并不影响图的联通性）然后发现去掉叶子节点的图变成了一条链。因为假设一个点有\(2\)个子树，由它连接的下一个点的子树就是它，所以下一个点至多还可以连一个子树，下下个点同理\(...\)

• 分类讨论：
  1.去掉叶子节点后图空了，原图只有两个点，\(ans = 2\)
  2.只剩一个点，原图是星形图，考虑中心点在那一边，剩下的叶子节点全排列，\(ans = 2 * (n-1)!\)
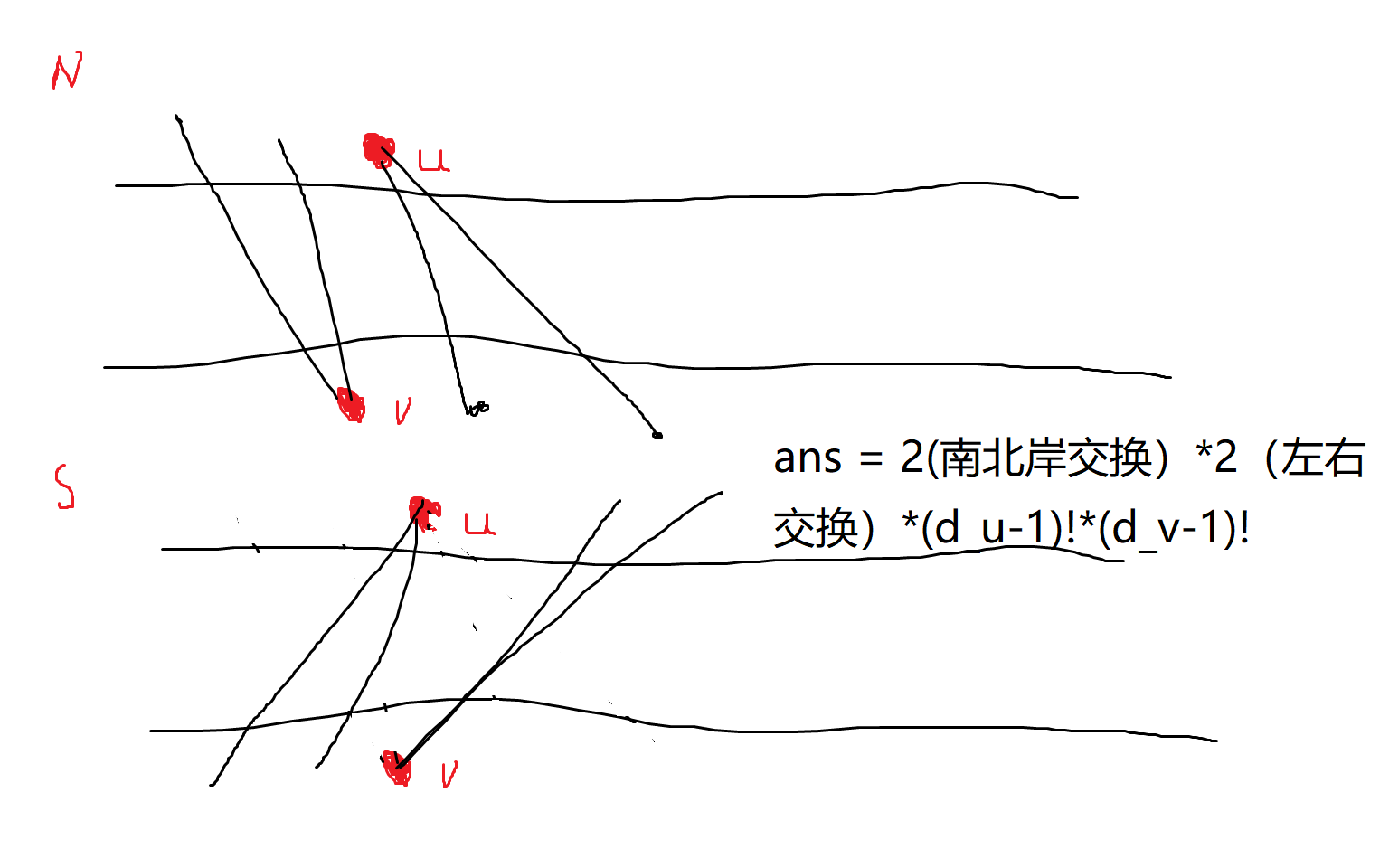
  3.剩两个点，
  
  4.剩三个点及以上
  $ans = 4 * $每个节点的叶子节点数的阶乘

code

#include <bits/stdc++.h>
using namespace std;
#define sz(x) int(x.size())

long long t, n, m, ans, tl;
vector <long long> g[200005];
long long fac[200005];
const long long MOD = 1e9 + 7;

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	fac[0] = 1;
	for(long long i = 1;i <= 200000;i++) fac[i] = fac[i - 1] * i % MOD;
	cin >> t;
	while(t--){
		ans = 2;
		tl = 0;
		cin >> n >> m;
		for(int i = 1;i <= n;i++) g[i].clear();
		for(int i = 1;i <= m;i++){
			int a, b;
			cin >> a >> b;
			g[a].push_back(b);
			g[b].push_back(a);
		}
		if(m >= n) ans = 0;
		for(int i = 1;i <= n;i++){
			if(sz(g[i]) > 1){
				int cnt = 0;
				for(int j = 0;j < sz(g[i]);j++){
					int v = g[i][j];
					if(sz(g[v]) == 1) cnt++;
				}
				if(sz(g[i]) - cnt <= 2) ans = ans * fac[cnt] % MOD;
				else ans = 0;
			}
			else tl++;
		}
		if(tl < n - 1) tl = 2;
		else tl = 1;
		cout<<ans * tl % MOD<<'\n';
	}
	return 0;
}

注意

#define int long long
#define sz(x) int(x.size())

会报错，
还要注意有符号整数溢出，特别是\(for\)循环里的\(i\)