2130C-Double Perspective

题目

对于一组对 $ S = {(a_1, b_1), (a_2, b_2), \ldots, (a_m, b_m)}$，其中对所有 \(1 \leq i \leq m\) 有 \(a_i < b_i\)，我们定义 \(f(S)\) 和 \(g(S)\) 如下：

• 将每个 \((a_i, b_i)\) 视为数轴上的一个线段，\(f(S)\) 是它们的并集长度。形式上，\(f(S)\) 是满足存在一个 \(i\)（\(1 \leq i \leq m\)）使得区间 \([x, x+1] \subseteq [a_i, b_i]\) 的整数 \(x\) 的数量。

• 将每个 \((a_i, b_i)\) 视为图中的无向边，\(g(S)\) 是至少存在一个包含至少3条边的简单环的节点数。形式上，\(g(S)\) 是满足存在路径 \(x_1 \to x_2 \to \cdots \to x_k \to x_1\)，其中 \(k \geq 3\)，且所有 \(x_1, x_2, \ldots, x_k\) 互不相同的节点 \(x_1\) 的数量。

例如，设 $ S = {(1,2), (2,4), (1,4), (4,5), (6,7)}$，则有 \(f(S) = 5\) 且 \(g(S) = 3\)。

给定 \(n\) 个不同的对。你的任务是从这些对中选择一个子集 \(S'\)，使得 \(f(S') - g(S')\) 最大化。你需要输出所选对的索引。

输入
每个测试包含多个测试用例。第一行包含测试用例数量 $ t$（\(1 \leq t \leq 10^4\)）。
测试用例描述如下。

每个测试用例的第一行包含一个整数 \(n\)（\(1 \leq n \leq 3 \cdot 10^3\)）。
接下来 \(n\) 行，每行包含两个整数 \(a_i\) 和 \(b_i\)（\(1 \leq a_i < b_i \leq 2n\)），表示一对。

保证每个测试用例中所有对都是不同的。
保证所有测试用例中 \(n^2\) 的总和不超过 \(9 \cdot 10^6\)。

输出
对于每个测试用例，第一行输出一个整数 \(k\)（\(0 \leq k \leq n\)）——选中子集 \(S'\) 的大小。
第二行输出 \(k\) 个整数 \(i_1, i_2, \ldots, i_k\)（\(1 \leq i_j \leq n\)），表示所选对的索引（索引必须不同）。

思路

想要\(f(s)-g(s)\)尽可能大，就要使\(f(s)\)大，给g(s)小。
假设\(g(s)\)为\(0\)时，图中无环，答案就是并集的大小，那答案一定是在\(g(s)=0\)时最大吗？


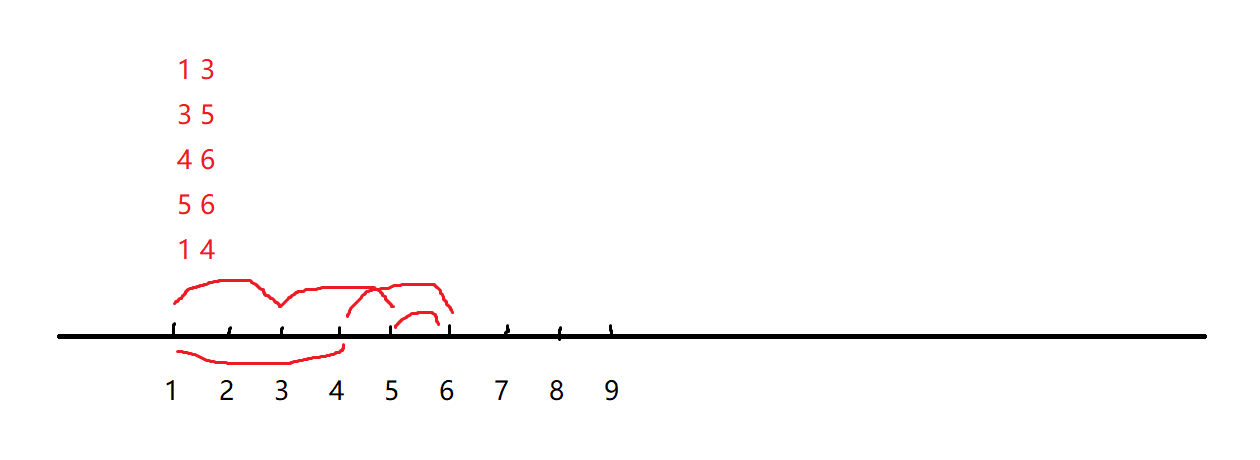
如果所选子集有环，那么在去掉一条边后，无环，且并集的大小不变，所以答案在\(g(s)=0\)时最大。

接下来要解决的问题是尽可能选更多的子集使并集更大，同时避免形成环。

观察一下形成环的特征是相邻两条边有共同的端点，例如上图的\((1，3)，(1，4)\),那么必有一条线段包含于另一条线段，再考虑必要性，如果有一条边被完全包围，那么就不选这一条边，就可以使图无环，时间复杂度\(O(n^2)\)