2119B - Line Segments

题目

你给定了两个点 \((p_x, p_y)\) 和 \((q_x, q_y)\) 在欧几里得平面上。

你从起点 \((p_x, p_y)\) 开始，将执行 \(n\) 次操作。在第 \(i\) 次操作中，你必须选择一个点，使得从你当前的位置到该点的欧几里得距离恰好为 \(a_i\)，然后移动到那个点。

确定在执行完所有操作后，是否可以到达终点 \((q_x, q_y)\)。

欧几里得距离 在两个点 \((x_1, y_1)\) 和 \((x_2, y_2)\) 之间的计算方法为
\( \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} \)

输入

每个测试包含多个测试用例。第一行包含测试用例的数量 \(t\) （\(1 \leq t \leq 10^4\)）。接下来的行描述测试用例。

每个测试用例的第一行包含一个整数 \(n\) （\(1 \leq n \leq 10^3\)）——序列 \(a\) 的长度。

每个测试用例的第二行包含四个整数 \(p_x, p_y, q_x, q_y\) （\(1 \leq p_x, p_y, q_x, q_y \leq 10^7\)）——起点和终点的坐标。

每个测试用例的第三行包含 \(n\) 个整数 \(a_1, a_2, \ldots, a_n\) （\(1 \leq a_i \leq 10^4\)）——每次操作的移动距离。

保证所有测试用例中 \(n\) 的总和不超过 \(2 \cdot 10^5\)。

输出

对于每个测试用例，如果在所有操作后能够到达终点 \((q_x, q_y)\)，则输出 "Yes"；否则输出 "No"。

你可以以任何形式输出答案（大小写均可）。例如，字符串 "yEs"、"yes"、"Yes" 都会被视为积极响应。

思路

将起点和终点看作一条边，这样一共就有\((++n)\)条边，询问是否可以围成一个多边形，可退化。

然后可以分类讨论：

\(1.\) \(if\) \(n \leq 3\),那么只要最长的边不大于其他边的长度和就可成立。

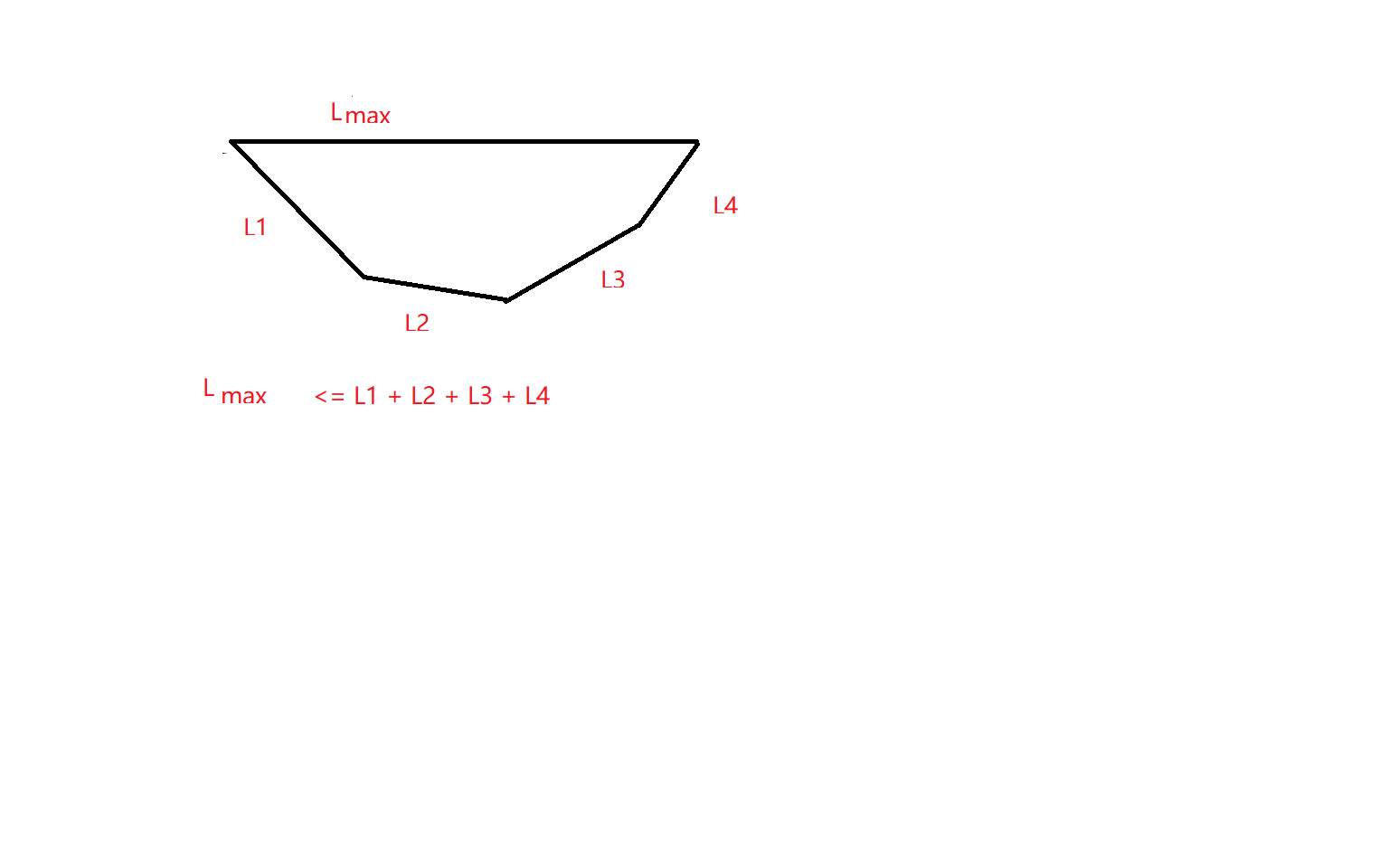
\(2.\) \(if\) \(n = 2\),那么只有两条边相等才可成立。

code

#include <bits/stdc++.h>
using namespace std;
#define int long long

int t;

void solve(){
	int n, px, py, qx, qy;
	double a, c[1005], maxn, sum;
	cin >> n;
	cin >> px >> py >> qx >> qy;
	n++;
	a = sqrt((double)(px - qx) * (px - qx) + (py - qy) * (py - qy));
	c[1] = a;
	maxn = a;
	sum = a;
	for(int i = 2;i <= n;i++){
		cin >> c[i];
		maxn = max(maxn, c[i]);
		sum += c[i];
	}
	if(maxn > sum - maxn){
		cout << "No" <<"\n";
		return;
	}
	if(n == 2){
		if(c[1] == c[2]) cout<<"Yes"<<"\n";
		else cout << "No" <<"\n";
	}
	else cout<<"Yes"<<"\n";
}

signed main(){
	cin >> t;
	while(t--){
		solve();
	}
	return 0;
}