深入理解傅里叶变换
1 基础概念
1.1 傅里叶级数
1 周期函数
若函数f(x)满足:存在非零常数T,对任意x有f(x+T) = f(x),则称f(x)为周期函数,T为其周期;最小正周期称为基本周期(记为T0)。傅里叶级数中,最常用以2π为周期的函数(T=2π),其他周期的函数可通过变量替换转化为2π周期,因此核心研究2π周期函数。
2 三角函数系的正交性
傅里叶级数的本质是在三角函数系中对周期函数做正交分解,类似平面向量在x、y轴上的分解,三角函数系就是周期函数空间的一组正交基。
(1)标准正交三角函数系(2π周期)
{1,cosx,sinx,cos2x,sin2x,…,cosnx,sinnx,…}
对上述三角函数系中任意两个不同的函数φm(x)和φn(x),满足:
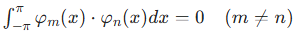
对同一个函数,积分结果非零:
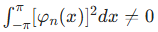
(3)核心正交积分公式
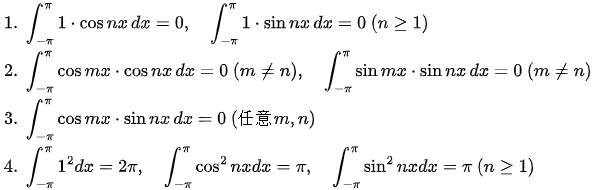
正交性的意义:三角函数系中的各个基函数“互不干扰”,分解后的每个正余弦项的系数可独立计算,这是傅里叶级数能求解的关键。
3 傅里叶级数
法国数学家傅里叶认为,任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示(选择正弦函数与余弦函数作为基函数是因为它们是正交的),后世称傅里叶级数为一种特殊的三角级数,根据欧拉公式,三角函数又能化成指数形式,也称傅立叶级数为一种指数级数。在数学中,三角级数是任何具有下述形式的级数:
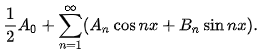
当An和Bn具有以下形式时,该级数称为傅立叶级数:
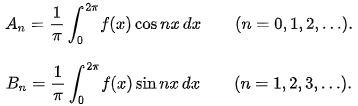
其中f(x)是可积函数。下面给出2π周期函数的傅里叶级数定义:
设f(x)是以2π为周期的函数,且在[-π, π]上可积,则其傅里叶级数为:
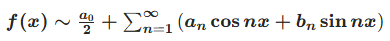
符号说明:
~:表示“展开为傅里叶级数”,而非严格相等(需满足收敛条件才相等);
a0/2:直流分量/零频项,是函数f(x)在一个周期内的平均值;
ancos nx:余弦项/偶次谐波,对应周期函数的偶函数分量;
bnsin nx:正弦项/奇次谐波,对应周期函数的奇函数分量;
a0, an, bn:傅里叶系数,是唯一确定的常数,有f(x)决定。
1.2 傅里叶变换
1 欧拉公式(Euler’s formula)
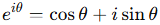
其中:e是自然常数,约等于2.71828,i是虚数单位满足i2=-1,θ是复指数的辐角∈R,对应复平面上的旋转角度。对于该公式当θ=π时,有eiπ + 1 = 0,这个公式在傅里叶变换中起到关键作用。
2 傅里叶变换(Fourier Transform, FT)
傅里叶变换是将时域的连续函数映射到频域连续函数的数学变换,是调和分析的核心工具,揭示了“任意连续周期/非周期函数均可分解为不同频率的正弦/余弦函数叠加”的本质。现给出连续傅里叶变换(Continuous Fourier Transform, CFT)相关定义,适用于定义域为全体实数R、满足狄利克雷条件(Dirichlet)的连续函数f(t),其中t为时域自变量(通常表示时间),变换后得到频域函数F(ω),ω为角频率(rad/s)。
(1)正变换(时域→频域)
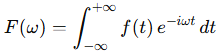
积分区间(−∞,+∞)对应非周期函数的时域是无限的,需对全体实数域积分,变换本质是:用所有频率的复指数函数作为“基函数”,对f(t)做投影。
(2)逆变换(频域→时域)
傅里叶变换是可逆变换,从频域函数F(ω)还原时域f(t)的公式为:
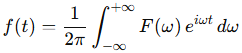
关键系数1/2π:该系数是为了满足“正逆变换的归一性”,也有教材将系数拆分为1/sqrt(2π)分别放在正、逆变换中(数学上更对称),两种形式等价。
3 离散傅里叶变换(Discrete Fourier Transform,DFT)
DFT是一种线性变换,把一个有限长的离散序列,从“时间/系数域”变换到“频率/点值域”。其数学定义为给定长度为n的复数序列:x=(x0, x1, ..., xn-1),令:ω = e-2πi/n,定义其离散傅里叶变换(DFT)为序列:
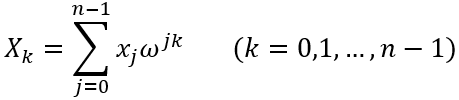
xj是输入序列(时域信号),Xk是输出序列(频域信号),通过将时域信号与一系列不同频率的复指数函数进行内积,得到每个频率分量在原始信号中的“含量”。DFT是一个线性变换,本质是X = F*x,其中F是一个范德蒙德(Vandermonde)矩阵,即从线性代数角度看:DFT = Vandermonde变换。从矩阵运算可以看出,要得到每个频率分量,需要进行n次乘法和n-1次加法运算,完成整个变换需要n2次乘法和n(n-1)次加法运算,所以完整变换的复杂度是O(n2),当序列长度n较大时,计算量会变得极其庞大,限制了DFT在实际应用中的效率。
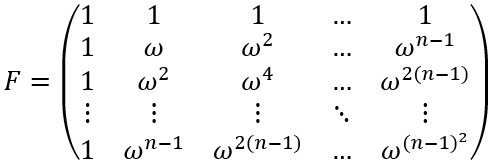
以多项式A(x)=a0+a1x+a2x2+...+an-1xn-1为例,则上述离散序列可以看作是多项式系数表示法(coefficient form)中的系数,即x = a = (a0, a1, ..., an-1),选择特殊的“点”——n次单位根:ω = e2πi/n,它满足:
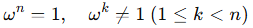
以n=11为例,图中所有ωi都是11次单位根:
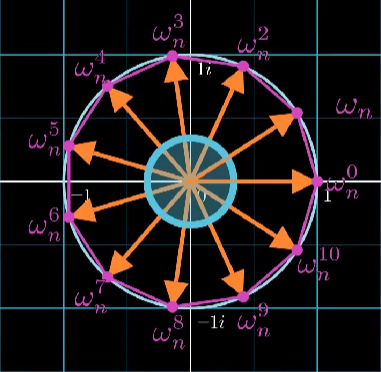
考虑n个互不相同的点:1, ω, ω2, ..., ωn-1,将其代入A(x)多项式,则有:
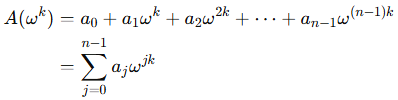
可见Xk = A(ω-k),即DFT的计算结果,恰好等价于在单位根上的多项式求值(对应多项式的点值表示法)。
逆离散傅里叶变换(IDFT)由以下公式给出:
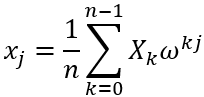
傅里叶级数、傅里叶变换和DFT区别由下表给出:

4 快速傅里叶变换(Fast Fourier Transform,FFT)
1965年,J.W.库利和T.W.图基提出了著名的Cooley-Tukey算法,即快速傅里叶变换(FFT)。FFT算法的核心是利用旋转因子的周期性、对称性和可约性,将长序列的DFT分解为短序列的DFT,从而大幅减少计算量。首先给出单位根的三个引理:
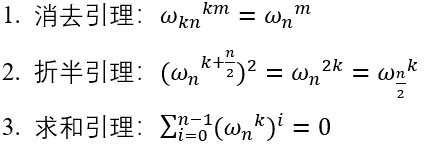
一句话概括FFT:利用n次单位根的周期性与对称性,把一个规模为n的DFT,拆成两个规模为N/2的DFT。在经典FFT算法(Cooley-Tukey算法)中假设n=2m,把序列拆成“偶数项+奇数项”:
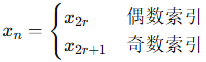
则可以将DFT拆开:
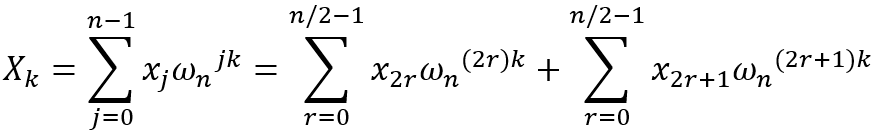
利用折半引理可将上式简化为:
![]()
其中:
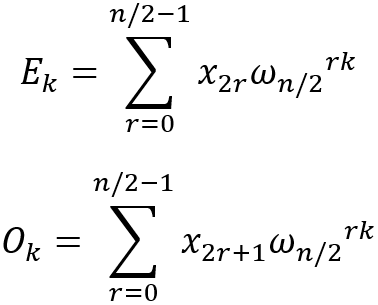
以上将1个包含n次乘法的DFT分成两个n/2次乘法的DFT,另外由ωnn/2+k = -ωnk可以进一步得到迭代公式(1):
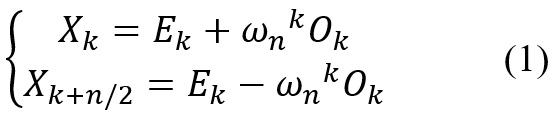
以上就是所谓的蝶形运算(butterfly),一次算出两个输出。可见一个长度为n的DFT被拆成两个长度是n/2的DFT和n/2次蝶形合并,所以时间复杂度为:
![]()
这里2T(n/2)表示:要解决一个规模为n的问题,需要“调用两次”规模为n/2的同类问题,每一次的代价是T(n/2);cn表示:当前这一层,为了把两个子FFT的结果“合并”所做的计算量。一个标准的radix-2蝶形:
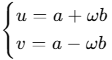
需要:1次复数乘法ωb和2次复数加减法,都是常数级操作可记为O(1),对于长度为n的FFT每一层有n/2个蝶形,所以每层蝶形计算量是n/2xO(1)=O(n),可以记为cn,这里的c就是一个蝶形需要多少个“基础运算”的常数因子。所以随着层数递增有以下时间复杂度推导:
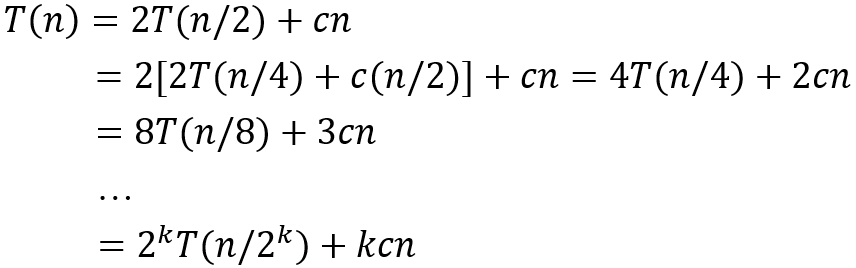
递归终止条件是当:n/2k=1,这时k=log2n,上述推导最终结果为:T(n)=n*T(1)+cnlog2n,忽略常数得最终复杂度公式T(n)=O(nlog2n)。
以上给出了快速傅里叶变换,快速傅里叶逆变换(IFFT,Inverse FFT)定义及分析过程与正变换类似,为了公式简洁正变换分析过程取ω = e-2πi/n,实际上在严格的数学定义中一般取ω = e2πi/n(正向单位根),此时正变换和逆变换定义如下:
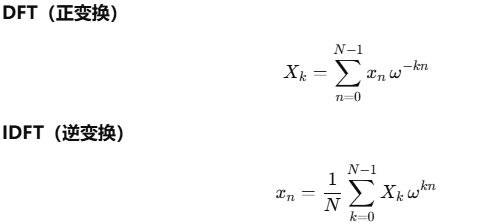
正变换用于拆解信号,获取在正交基上的投影,逆变换用于合成信号,完成正交基投影的叠加。
1.3 NTT(Number Theoretic Transform)
NTT = 在有限域/模整数环中进行的FFT,即NTT是把FFT中的“复数单位根”换成了“模意义下的单位根”,结构完全一致,只是“数域”不同。FFT主要存在3方面问题:用的是复数、有浮点误差、在密码学/大整数/精确多项式运算中不可接受,而NTT正好可以解决这些问题。NTT工作空间是有限域,通常选Fp,p是素数,所有运算都基于mod p,在NTT中,需要找ω(模p下的n次原始单位根),它满足:
![]()
设模数p,n|(p-1),ω是n次原始单位根,NTT相关定义如下:
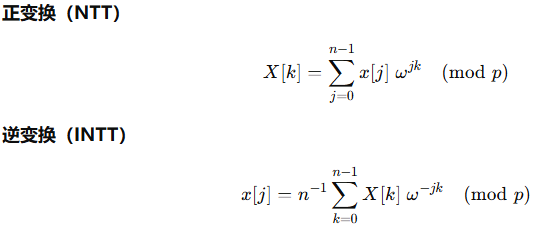
和FFT相关对比如下:
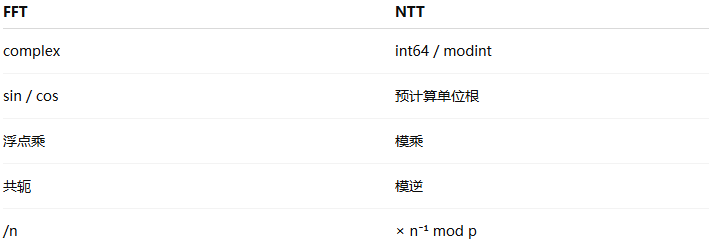
2 算法实现
理解了FFT的数学原理后,我们需要将其转化为可执行的代码。FFT算法有多种实现方式,包括递归实现、迭代实现和基于特定平台的优化实现。
2.1 递归实现FFT
递归实现是最直观的FFT实现方式,它直接对应Cooley-Tukey算法的分治思想。递归算法不断将问题分解为更小的子问题,直到达到基本情况(2点或1点DFT)。

import numpy as np import matplotlib.pyplot as plt # 设置字体,确保中文显示 plt.rcParams['font.sans-serif'] = ['SimHei'] plt.rcParams['axes.unicode_minus'] = False def fft_recursive(x): """ 递归实现快速傅里叶变换 注意:输入向量x的长度必须是2的幂次 """ n = len(x) if n == 1: return x # 分别计算偶数索引和奇数索引元素的FFT even_fft = fft_recursive(x[0::2]) # 偶数索引 odd_fft = fft_recursive(x[1::2]) # 奇数索引 # 计算旋转因子 w = [np.exp(-2j * np.pi * k / n) for k in range(n//2)] # 组合结果 result = np.zeros(n, dtype=complex) for k in range(n//2): term = w[k] * odd_fft[k] result[k] = even_fft[k] + term result[k + n//2] = even_fft[k] - term return result # 测试递归FFT def test_fft_recursive(): # 生成测试信号:50Hz和120Hz正弦波的叠加 fs = 1000 # 采样频率1000Hz t = np.linspace(0, 1, 1024) # 1秒时间,1024个点 signal = np.sin(2 * np.pi * 50 * t) + 0.5 * np.sin(2 * np.pi * 120 * t) # 计算FFT fft_result = fft_recursive(signal) # 计算频率轴 freqs = np.fft.fftfreq(len(signal), 1/fs) print(len(freqs)) # 绘制结果 plt.figure(figsize=(12, 4)) plt.subplot(1, 2, 1) plt.plot(t, signal) plt.title('原始信号') plt.xlabel('时间 (s)') plt.ylabel('幅度') plt.subplot(1, 2, 2) plt.plot(freqs[:len(freqs)//2], np.abs(fft_result[:len(fft_result)//2])) plt.title('频谱图') plt.xlabel('频率 (Hz)') plt.ylabel('幅度') plt.xlim(0, 200) plt.tight_layout() plt.show() if __name__ == "__main__": test_fft_recursive()
程序中以50Hz和120Hz正弦波叠加产生测试信号,通过FFT变换可以这两个信号快速的过滤出来:
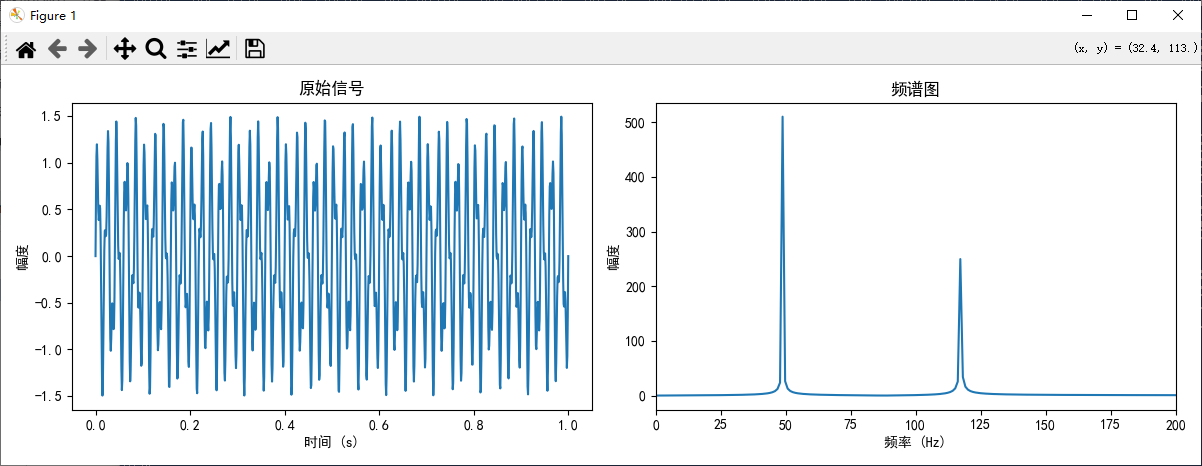
递归实现虽然直观,但存在一些缺点:
1. 递归调用会产生额外的函数调用开销
2. 需要不断创建新的子数组,内存使用不够高效
3. 对于大数组,可能导致递归深度过大
因此,在实际应用中,迭代实现通常更受青睐。
2.2 迭代实现FFT
迭代FFT算法通过循环而非递归实现计算,效率更高。迭代算法的核心是首先对输入数组进行位反序排列,然后通过多层循环实现蝶形运算。首先以n=8为例,看下X0的重排序,由于ω0=1则根据DFT公式可知:
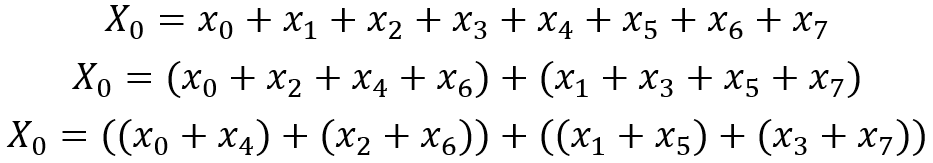
观察以下二进制下标,可知重排序后的二进制下标正是正序下标二进制的逆序,把这种序列叫做逆二进制序:
0 4 2 6 1 5 3 7
000 100 010 110 001 101 011 111
000 001 010 011 100 101 110 111
0 1 2 3 4 5 6 7
同理可以给出X1及X4=X0+8/2的迭代计算过程:
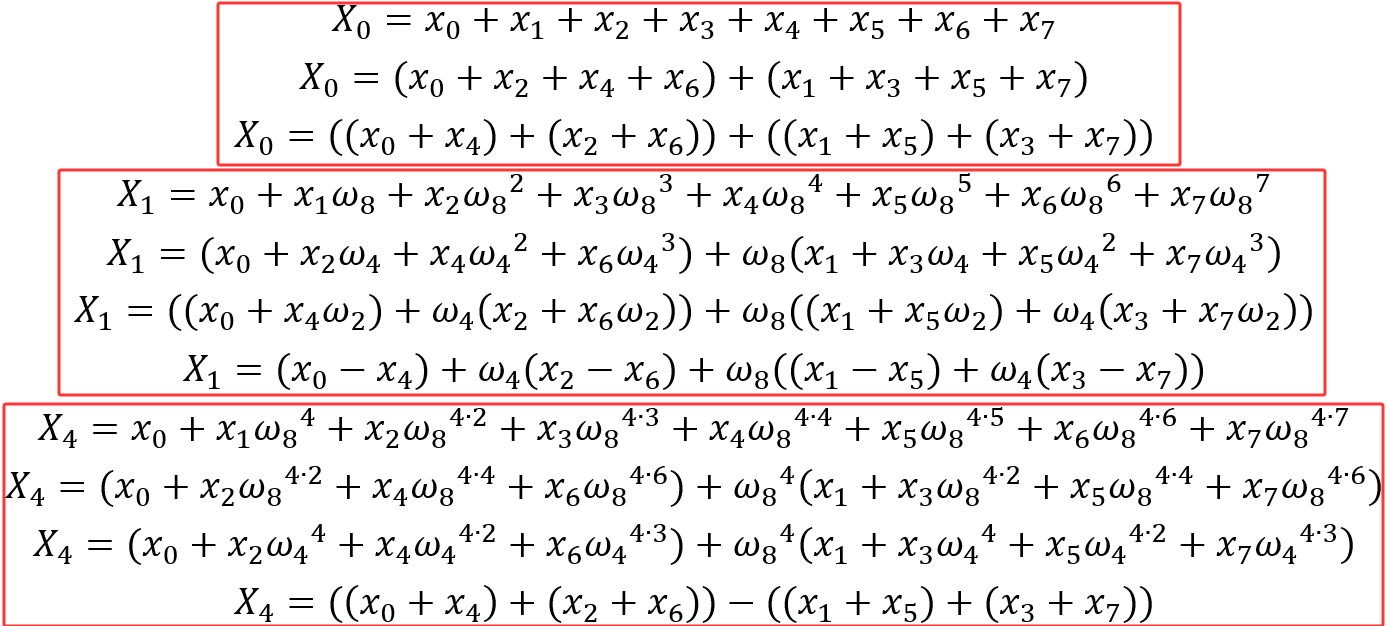
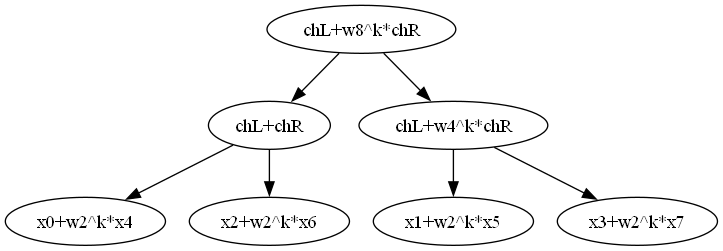
X0和X4完全对应迭代公式(1),实际上所有Xk计算过程可以由以下二叉树给出:

1 import numpy as np 2 import matplotlib.pyplot as plt 3 4 # 设置字体,确保中文显示 5 plt.rcParams['font.sans-serif'] = ['SimHei'] 6 plt.rcParams['axes.unicode_minus'] = False 7 8 def bit_reverse(n, num_bits): 9 """将n的二进制表示进行位反序""" 10 reversed_n = 0 11 for i in range(num_bits): 12 if n & (1 << i): 13 reversed_n |= (1 << (num_bits - 1 - i)) 14 return reversed_n 15 16 def fft_iterative(x): 17 """ 18 迭代实现快速傅里叶变换 19 输入x的长度必须是2的幂次 20 """ 21 n = len(x) 22 num_bits = int(np.log2(n)) 23 24 # 位反序排列 25 reversed_index = [bit_reverse(i, num_bits) for i in range(n)] 26 data = x[reversed_index].astype(complex) 27 28 # 迭代计算FFT 29 size = 2 30 while size <= n: 31 half_size = size // 2 32 # 计算旋转因子 33 w_m = np.exp(-2j * np.pi / size) 34 35 for k in range(0, n, size): 36 w = 1 37 for j in range(half_size): 38 t = w * data[k + j + half_size] 39 u = data[k + j] 40 data[k + j] = u + t 41 data[k + j + half_size] = u - t 42 w *= w_m 43 size *= 2 44 45 return data 46 47 # 测试迭代FFT 48 def test_fft_iterative(): 49 # 生成测试信号 50 n = 256 # 数据点个数,必须是2的幂次 51 fs = 1000 # 采样频率 52 53 t = np.linspace(0, 1, n) 54 # 生成包含多个频率成分的信号 55 signal = (np.sin(2 * np.pi * 50 * t) + 56 0.5 * np.sin(2 * np.pi * 120 * t) + 57 0.3 * np.sin(2 * np.pi * 200 * t)) 58 59 # 添加噪声 60 noise = 0.2 * np.random.normal(size=n) 61 signal += noise 62 63 # 计算FFT 64 fft_result = fft_iterative(signal) 65 freqs = np.fft.fftfreq(n, 1/fs) 66 67 # 与NumPy内置FFT对比 68 np_fft = np.fft.fft(signal) 69 70 # 绘制结果 71 plt.figure(figsize=(15, 5)) 72 73 plt.subplot(1, 3, 1) 74 plt.plot(t, signal) 75 plt.title('原始信号 (含噪声)') 76 plt.xlabel('时间 (s)') 77 plt.ylabel('幅度') 78 79 plt.subplot(1, 3, 2) 80 plt.plot(freqs[:n//2], np.abs(fft_result[:n//2]), label='自定义FFT') 81 plt.title('自定义FFT频谱') 82 plt.xlabel('频率 (Hz)') 83 plt.ylabel('幅度') 84 plt.xlim(0, 300) 85 86 plt.subplot(1, 3, 3) 87 plt.plot(freqs[:n//2], np.abs(np_fft[:n//2]), label='NumPy FFT', color='orange') 88 plt.title('NumPy FFT频谱') 89 plt.xlabel('频率 (Hz)') 90 plt.ylabel('幅度') 91 plt.xlim(0, 300) 92 93 plt.tight_layout() 94 plt.show() 95 96 # 计算误差 97 error = np.max(np.abs(fft_result - np_fft)) 98 print(f"与NumPy FT的最大误差: {error}") 99 100 if __name__ == "__main__": 101 test_fft_iterative()
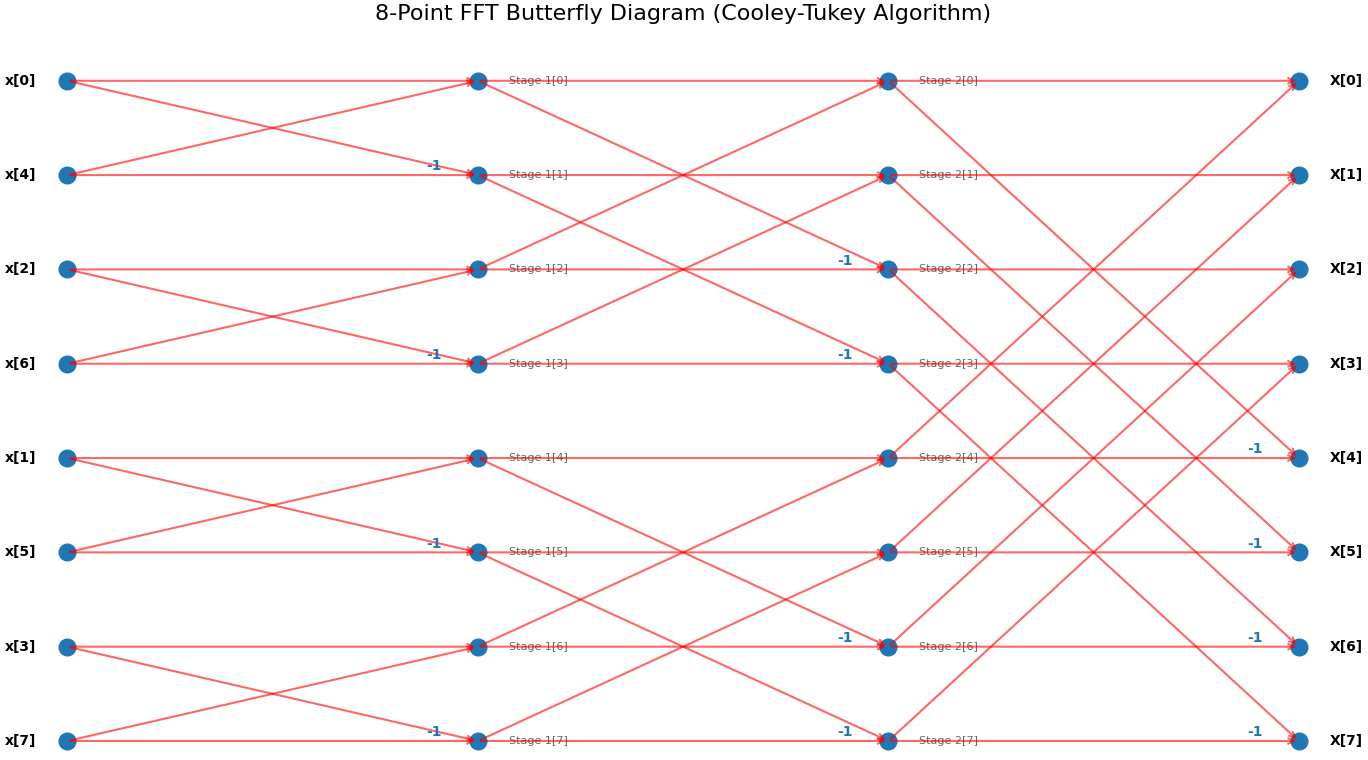
仍以n=8为例,迭代算法中首先对输入进行二进制的逆序,然后进行3个阶段的蝶形计算,第1个阶段由相邻点产生下一级的输出,第2个阶段由间隔一个点的输入产生输出,第3个阶段由间隔两个点的输出产生输出,蝴蝶由瘦变胖,如下图所示:
3 应用实例
3.1 音频处理中的应用
FFT(快速傅里叶变换)是音频领域的核心数字信号处理工具,本质是将音频的时域信号(随时间变化的声波振幅)转换为频域信号(不同频率的声音分量占比),而人耳对声音的感知本身就是基于频率的(如音调、音色),这使得 FFT 成为音频采集、分析、处理、合成全链路的基础。
1 音频基础分析
所有音频智能分析的前提,核心是将不可直接解读的时域波形,转换为可量化的频率特征。
核心逻辑
(1)音频在计算机中是采样率固定的时域离散数据(如44.1kHz采样率 = 1秒采集44100个振幅值),波形仅能反映声音的强弱变化,无法直接得到音调、音色等关键信息;
(2)对时域音频段执行一维 FFT,得到频谱(横坐标为频率,纵坐标为对应频率的振幅/能量),频谱直接反映 “哪些频率的声音构成了当前音频”;
(3)针对非平稳音频(声音频率随时间变化,如说话、唱歌、乐器演奏),采用STFT(短时傅里叶变换):将音频切分为连续的短帧(如20ms/帧),对每帧独立做FFT,最终得到时频图(横轴时间,纵轴频率,颜色 / 亮度表示能量),实现 “时间-频率” 的二维分析。
典型应用
音频软件的频谱分析仪(如 Audition、Cool Edit):实时显示音频的频率分布,帮助调音师判断声音的频率缺陷;
基础音频特征提取:通过 FFT 计算基频(Fundamental Frequency,F0)(声音的基础音调,如男声基频 80-200Hz,女声 200-500Hz)、谐波(基频的整数倍频率,决定音色)、频谱能量(决定声音响度)。
2 音调检测与音高识别(Pitch Detection)
音调是音频最核心的感知特征之一,FFT是实现音高识别的经典算法基础,广泛用于K歌评分、乐器校音、语音识别。
核心逻辑
(1)纯音(如钢琴单键)的时域波形是周期性的,其频域频谱中能量最高的频率即为基频(F0),对应听觉上的音调;
(2)对乐器/人声的混合音频,通过FFT得到频谱后,筛选出基频峰(主峰值)和其谐波峰,通过峰值检测算法确定实际音高;
(3)工程中会结合自相关法优化FFT的基频检测,解决低信噪比、谐波干扰下的检测误差问题。
典型应用
(1)乐器校音软件(如吉他校音器、钢琴校音器):实时采集乐器声音,通过FFT检测基频,对比标准音高(如 A4=440Hz)给出校音提示;
(2)K歌APP的音高评分(如唱吧、全民K歌):实时分析演唱声音的基频,与原唱基频对比,判断音准并打分;
(3)音乐乐谱自动转写:将演奏音频转换为五线谱,核心是通过 FFT 逐帧检测音高并匹配对应音符。
3 音频滤波:精准去除噪声/保留目标频率
音频滤波是FFT最常用的处理类应用,相比传统的模拟滤波,基于FFT的频域滤波更灵活、精准,可实现任意自定义的频率筛选,核心是 “频域修改,时域重构”。
核心逻辑(与图像 FFT 压缩原理同源)
(1)时域→频域:对音频帧执行 FFT,得到频域系数;
(2)频域滤波:根据需求生成频率掩码,对频域系数做修改:
低通滤波:保留低频系数,置零高频系数(如去除音频中的高频嘶嘶噪声);
高通滤波:保留高频系数,置零低频系数(如去除音频中的低频底噪、电流声);
带通滤波:仅保留指定频率区间的系数(如提取人声音频,保留 300-3400Hz 的人声核心频率);
带阻滤波 / 陷波滤波:置零指定频率区间的系数(如去除 50Hz/60Hz 的市电工频噪声);
(3)频域→时域:对滤波后的频域系数执行逆 FFT(IFFT),转换回时域音频,得到滤波后的声音。
典型应用
(1)语音降噪(如会议录音、麦克风降噪):通过FFT去除背景中的低频底噪、高频环境噪声,保留人声;
(2)音乐制作中的均衡器(EQ):对音乐的低频、中频、高频分别做增益 / 衰减(本质是修改FFT后的频域系数振幅),调整音乐的音色层次;
(3)广播/直播的音频处理:过滤掉人声外的无效频率,提升声音的清晰度。
4 声音合成与音色模拟(加法合成 / 调频合成)
声音的音色由“基频+谐波的频率分布比例”决定,FFT为音色的量化和合成提供了基础,是电子音乐、语音合成的核心技术之一。
核心逻辑
(1)音色的频域本质:不同乐器的同一音调(基频相同),音色不同的原因是谐波的数量、振幅占比不同(如钢琴的谐波丰富且高频衰减快,小提琴的高频谐波更突出);
(2)加法合成:通过 FFT 分析目标乐器的频谱(基频 + 各谐波的能量比例),然后用多个正弦波(对应基频和各谐波)按该比例叠加,合成出与目标乐器相似的音色;
(3)语音合成(TTS):对真人语音做 FFT 分析,得到不同音节的频谱特征,合成时通过调整基频和频谱分布,生成自然的人工语音。
典型应用
(1)电子音乐合成器(如FL Studio、Ableton Live):基于 FFT 的频谱分析,模拟钢琴、吉他、弦乐等传统乐器的音色,或制作自定义的电子音色;
(2)语音合成引擎(如讯飞TTS、百度TTS):通过 FFT 提取语音的频谱特征,提升合成语音的自然度;
(3)声音特效制作:如将人声转换为机器人声(通过FFT修改频谱,压制谐波,保留基频)。
5 音频特征提取与智能分析(AI / 机器学习基础)
当下的音频智能应用(如语音识别、声纹识别、音频分类),其核心特征均基于 FFT 的频域分析,FFT 是连接原始音频数据和 AI 模型的桥梁。
核心逻辑
(1)原始时域音频数据维度高、冗余大,无法直接输入AI模型;
(2)通过 FFT/STFT 将音频转换为频域特征,再进一步提取梅尔频谱(Mel Spectrogram)、梅尔频率倒谱系数(MFCC) 等工程化特征:
梅尔频谱:将 FFT 得到的线性频谱转换为符合人耳听觉特性的梅尔刻度频谱(人耳对低频更敏感,对高频更迟钝);
MFCC:对梅尔频谱做离散余弦变换(DCT),提取的低维系数,是语音识别、声纹识别的经典核心特征;
(3)这些频域特征维度低、辨识度高,是语音识别、音频分类模型的标准输入。
典型应用
(1)语音识别(ASR):如微信语音转文字、讯飞听见,核心特征是MFCC,其提取基础是FFT/STFT;
(2)声纹识别:如手机声纹解锁、银行语音验证,通过 FFT 分析不同人的语音频谱特征(声纹),实现身份识别;
(3)音频分类:如短视频的背景音乐识别、环境声检测(如哭声、玻璃破碎声、汽车鸣笛声),基于梅尔频谱做模型训练,而梅尔频谱的基础是FFT;
(4)音乐推荐:通过FFT分析歌曲的频谱特征(如低频能量占比、节奏对应的频率变化),对歌曲做分类,实现个性化推荐。
6 音频同步与匹配(如音频指纹、音视频同步)
(1)音频指纹(Audio Fingerprint)
核心是通过FFT对音频的时频特征做提取,生成唯一的 “音频指纹”,实现音乐识别、音频查重。如摇一摇识曲(QQ音乐、网易云音乐),通过FFT提取待识别音频的时频特征,与服务器中的音频指纹库匹配,快速识别歌曲名称。
(2)音视频同步
视频的画面帧与音频的时间轴易出现错位,通过FFT分析音频的频谱特征变化,与视频的画面特征变化做时间对齐,实现音视频同步校正。
3.2 图像处理中的应用
FFT在图像处理中主要用于频域滤波、图像压缩、纹理分析等。接下来以图像压缩为例进行说明。
图像在计算机中以像素矩阵存储,这是空间域表示:每个数值代表对应位置的亮度/颜色,直观描述图像的空间分布,但数据冗余度高。频域是通过傅里叶变换得到的另一种表示形式,将图像分解为不同频率的正弦/余弦波叠加,频率描述的是像素值的变化快慢:
低频分量:像素值变化缓慢,对应图像的整体轮廓、大面积平滑区域、主体结构(如人脸轮廓、天空背景);
高频分量:像素值变化剧烈,对应图像的细节纹理、边缘、噪声、微小瑕疵(如发丝、文字边缘、噪点)。
人眼的视觉特性与图像频域特性高度匹配:
人眼对整体轮廓、大面积区域(低频信息)高度敏感,是识别图像的核心依据;
人眼对精细纹理、微小噪声(高频信息)敏感度较低,适度舍弃后,肉眼难以察觉明显失真;
结合这一特性,FFT 压缩可以在保证主观视觉质量的前提下,实现可观的数据压缩。举个例子:一张风景照,蓝天、山脉轮廓是低频核心信息,树叶纹理、水面波纹是高频信息,舍弃 80% 高频系数后,图像依然可清晰识别,仅会轻微模糊。
图像是二维信号,需要使用二维离散傅里叶变换(2D-DFT)完成空间域到频域的转换,FFT图像压缩的本质是利用频域能量分布的不对称性,实现有损数据压缩,完整逻辑分为4个核心步骤:
步骤 1:空间域 → 频域转换(FFT)
对图像(或图像分块)执行二维FFT,将像素值转换为频域系数(复数形式,包含幅度和相位信息)。变换后,默认低频系数分布在频域矩阵的四角,高频在中心;通过fftshift中心化后,低频集中在矩阵中心,高频分布在四周,方便筛选处理。
步骤 2:频域系数量化与截断(核心压缩操作)
基于能量集中特性执行压缩操作:
(1)保留携带绝大部分图像能量的低频系数;
(2)直接舍弃/置零仅携带少量细节、噪声的高频系数;
(3)舍弃的高频信息越多,压缩率越高,图像失真越明显。
一般通过计算频域点到中心的欧式距离筛选低频系数,距离中心越近,频率越低,这是最常用的低频筛选方式。
步骤 3:逆变换重构图像(逆 FFT)
对处理后的频域系数执行逆移位(ifftshift)+ 逆FFT(ifft2),将频域信号转换回空间域,得到压缩重构后的图像。由于逆 FFT 结果会存在微小虚部(浮点计算误差),只需提取实部即可得到有效像素值。
步骤 4:数据存储优化
原始图像存储每个像素的空间域数据,而压缩后仅需存储少量保留的低频系数,大幅减少数据量,实现存储/传输的压缩效果。
以下是源码:

import numpy as np import matplotlib.pyplot as plt import matplotlib.image as mpimg import os from math import log10, sqrt from PIL import Image # 新增:用PIL保存图像,兼容所有版本 # 设置中文显示 plt.rcParams['font.sans-serif'] = ['SimHei'] plt.rcParams['axes.unicode_minus'] = False def psnr(original, compressed): """计算峰值信噪比(PSNR),兼容彩色/灰度图""" # 若原始图像是彩色图,先转为灰度图再计算PSNR if len(original.shape) == 3: original_gray = np.mean(original, axis=2).astype(np.uint8) else: original_gray = original.astype(np.uint8) # 确保压缩后图像是uint8类型 compressed = compressed.astype(np.uint8) # 计算MSE(均方误差) mse = np.mean((original_gray - compressed) ** 2) if mse == 0: # 无误差 return float('inf') max_pixel = 255.0 psnr_value = 20 * log10(max_pixel / sqrt(mse)) return psnr_value def fft_image_compress(image, block_size=8, keep_ratio=0.1): """基于FFT的图像压缩(自动处理彩色/灰度图)""" # 1. 彩色图转灰度图(压缩只处理灰度,保留核心逻辑) if len(image.shape) == 3: image_gray = np.mean(image, axis=2).astype(np.uint8) else: image_gray = image.astype(np.uint8) h, w = image_gray.shape # 2. 补零使图像尺寸为block_size的整数倍 pad_h = (block_size - h % block_size) % block_size pad_w = (block_size - w % block_size) % block_size print("h {} w {} pad_h {} pad_w {}".format(h, w, pad_h, pad_w)) image_padded = np.pad(image_gray, ((0, pad_h), (0, pad_w)), mode='constant') h_pad, w_pad = image_padded.shape # 3. 初始化压缩后的频域数组 fft_compressed = np.zeros_like(image_padded, dtype=np.complex128) # 4. 分块FFT+高频截断 for i in range(0, h_pad, block_size): for j in range(0, w_pad, block_size): block = image_padded[i:i+block_size, j:j+block_size] # 2D-FFT:空间域→频域(中心化,低频移到中心) fft_block = np.fft.fft2(block) # 对图像块做二维 FFT,将空间域的像素值转换为频域的复数系数(低频默认在四角,高频在中心 fft_block_shifted = np.fft.fftshift(fft_block) # 将频域系数 “中心化”,把低频系数移到频域矩阵的中心,高频系数分布在四周,方便后续筛选低频 # 计算需要保留的低频系数数量 total_coeffs = block_size * block_size # 单个图像块的总系数数(等于像素数) keep_coeffs = int(total_coeffs * keep_ratio) # 预设的保留比例(如0.1表示保留10%的系数) keep_coeffs = max(keep_coeffs, 1) # 防止保留系数为0,保证至少保留1个低频系数,避免重构失败 # 生成掩码:只保留低频系数,高频置0 center = block_size // 2 # 频域矩阵的中心坐标(如 block_size=8 时,center=4) y, x = np.ogrid[:block_size, :block_size] # 生成网格坐标矩阵,对应每个系数在频域中的位置 distance = np.sqrt((y - center)**2 + (x - center)**2) # 计算每个系数到中心的欧式距离(距离越小,频率越低) flat_distance = distance.flatten() # 将距离矩阵展平为一维数组,方便排序 idx = np.argsort(flat_distance)[:keep_coeffs] # 对距离从小到大排序,取前keep_coeffs个索引(对应距离中心最近的低频系数) mask_flat = np.zeros(total_coeffs, dtype=bool) # 生成布尔掩码mask:维度与图像块一致 mask_flat[idx] = True # mask中True的位置对应保留的低频系数,False对应舍弃的高频系数 mask = mask_flat.reshape((block_size, block_size)) # 应用掩码:高频系数置零 fft_block_shifted[~mask] = 0 # ~mask:取掩码的反(False变True,True变False),即高频系数的位置。 # 将频域矩阵中高频系数的位置置为 0,只保留低频系数,实现 “压缩”(丢弃高频信息) # 逆移位+逆FFT:频域→空间域 fft_block = np.fft.ifftshift(fft_block_shifted) # 逆中心化,将频域系数恢复到 FFT 后的原始位置(低频回到四角) ifft_block = np.fft.ifft2(fft_block) # 对处理后的频域系数做逆 FFT,转换回空间域(结果为复数) block_recon = np.real(ifft_block) # 取复数的实部(因舍入误差可能有微小虚部,需剔除),得到重构后的图像块像素值 # 存入压缩后数组 fft_compressed[i:i+block_size, j:j+block_size] = block_recon # 将重构后的图像块放回fft_compressed数组的对应位置,最终拼接成完整的压缩后图像 # 5. 去除补零,恢复原始尺寸 compressed_image = fft_compressed[:h, :w] # 限制像素值范围(0~255),避免溢出 compressed_image = np.clip(compressed_image, 0, 255).astype(np.uint8) # 6. 计算压缩比(频域系数层面) total_original_coeffs = h_pad * w_pad total_keep_coeffs = (h_pad * w_pad) * keep_ratio compression_ratio = total_original_coeffs / total_keep_coeffs return compressed_image, compression_ratio def save_image_with_quality(image, path, quality=95): """ 兼容所有版本的图像保存函数,支持设置JPG质量 :param image: 灰度图像数组(uint8,0~255) :param path: 保存路径(如"test.jpg") :param quality: JPG质量(0~100,值越小压缩越狠) """ # 将numpy数组转为PIL Image对象 pil_img = Image.fromarray(image) # 保存为JPG,设置质量参数 pil_img.save(path, "JPEG", quality=quality) # 主函数:测试FFT图像压缩 if __name__ == "__main__": # 1. 读取图像(替换为你的图像路径) image_path = "1.jpg" # 支持彩色/灰度图 try: original_image = mpimg.imread(image_path) # 注意:matplotlib读取的图像像素值是0~1的浮点数,需转回0~255 if original_image.dtype == np.float32: original_image = (original_image * 255).astype(np.uint8) except FileNotFoundError: print("错误:未找到图像文件,自动生成测试灰度图...") # 生成512×512渐变灰度图作为测试 original_image = np.linspace(0, 255, 512*512).reshape(512, 512).astype(np.uint8) # 2. 执行FFT压缩(调整keep_ratio控制压缩比) compressed_image, compress_ratio = fft_image_compress( original_image, block_size=8, keep_ratio=0.1 ) # 3. 计算PSNR(修复维度不匹配问题) psnr_value = psnr(original_image, compressed_image) # 4. 保存图像(改用PIL,支持quality参数,兼容所有版本) # 保存原图(转灰度后保存,统一对比基准) if len(original_image.shape) == 3: original_gray = np.mean(original_image, axis=2).astype(np.uint8) else: original_gray = original_image save_image_with_quality(original_gray, "original_gray.jpg", quality=95) # 保存压缩后图像,设置JPG质量(值越小文件越小) save_image_with_quality(compressed_image, "compressed_final.jpg", quality=50) # 5. 计算实际文件大小(KB) original_size = os.path.getsize("original_gray.jpg") / 1024 if os.path.exists("original_gray.jpg") else 0 compressed_size = os.path.getsize("compressed_final.jpg") / 1024 if os.path.exists("compressed_final.jpg") else 0 actual_compression_ratio = original_size / compressed_size if (compressed_size > 0 and original_size > 0) else 0 # 6. 显示结果 plt.figure(figsize=(12, 6)) # 原图(彩色/灰度自适应显示) plt.subplot(1, 2, 1) if len(original_image.shape) == 3: plt.imshow(original_image) else: plt.imshow(original_image, cmap='gray') plt.title(f'原始图像\n尺寸:{original_image.shape[1]}×{original_image.shape[0]}\n大小:{original_size:.2f} KB') plt.axis('off') # 压缩后图像(灰度) plt.subplot(1, 2, 2) plt.imshow(compressed_image, cmap='gray') plt.title(f'FFT压缩后图像\n理论压缩比:{compress_ratio:.1f}:1\n实际文件压缩比:{actual_compression_ratio:.1f}:1\nPSNR:{psnr_value:.2f} dB') plt.axis('off') plt.tight_layout() plt.show() # 打印详细信息 print(f"=== 压缩结果 ===") print(f"理论频域压缩比:{compress_ratio:.1f}:1") print(f"实际文件压缩比:{actual_compression_ratio:.1f}:1") print(f"原始文件大小:{original_size:.2f} KB") print(f"压缩后文件大小:{compressed_size:.2f} KB") print(f"PSNR(图像质量):{psnr_value:.2f} dB")
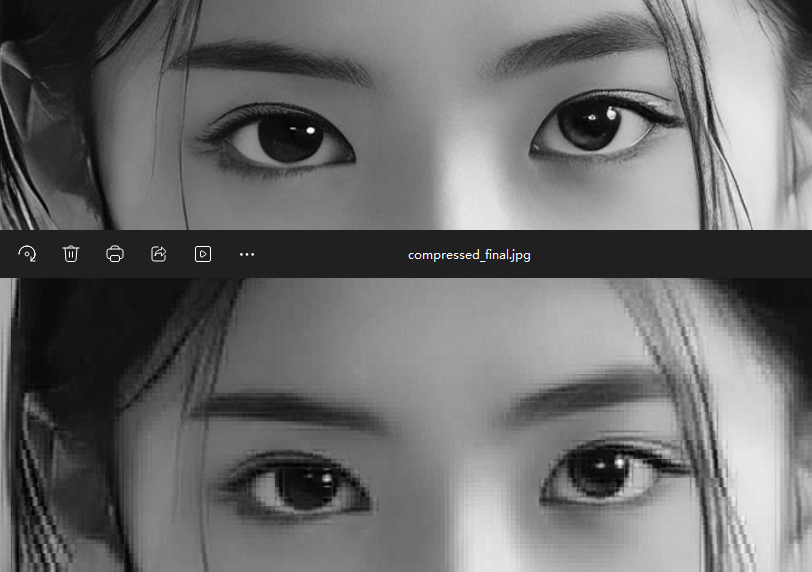
程序运行效果如下:

因为运行结果显示分辨率不高,看起来压缩后的图片和原图并没有太大的不同,但是将图片放大以后还是可以明显看出压缩后图片的失真:
参考:
1 https://zhuanlan.zhihu.com/p/19763358
2 https://www.cnblogs.com/xxeray/p/fast-fourier-transform.html
3 https://blog.csdn.net/qq_42212808/article/details/156030009



 浙公网安备 33010602011771号
浙公网安备 33010602011771号