SEAL全同态加密BFV方案入门详解

Microsoft SEAL（Simple Encrypted Arithmetic Library）是微软开源的轻量级、高性能全同态加密（FHE）库，专为整数/浮点数的密文运算设计，支持BFV、CKKS、BGV等主流FHE方案，广泛应用于隐私计算、联邦学习、数据加密等场景，源码：https://github.com/microsoft/SEAL。

1 数学基础

1.1 多项式环

SEAL使用的基础环是：

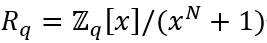
BFV的所有运算都在这个多项式环中进行，符号含义如下：

Z_q：系数域，即多项式的所有系数都取自“模q的整数集合”，q称为系数模数（一个大素数或多个素数的乘积），决定密文的噪声容忍度和运算深度。

x^N+1：多项式模，要求N是2的整数幂（如4096、8192），满足x^N≡-1 (mod x^N+1)，这意味着所有多项式的次数都不会超过N-1（超过的项可通过x^N = -1降次）。

R_q元素形式：任意元素是一个次数≤ N - 1的多项式，形如：

 

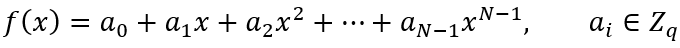
1.2 明文空间

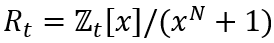
明文（待加密的整数）会被编码为R_t中的多项式，t满足t≡1 (mod 2N)，这是批量加密的硬性要求，明文在进行加密前要进行编码，有两种编码方式：

单整数编码：将单个整数m编码为常数多项式f(x)=m，即所有高次项系数为0。

批量编码：将N个小整数[m₀,m₁,...,m_N-1]直接做为多项式的系数，编码为：

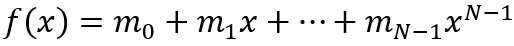
1.3 RLWE问题

BFV的安全性基于RLWE问题（Ring Learning With Errors）的计算困难性，简单描述为：

给定多项式R_q，选择一个秘密多项式s(x)∈R_q（系数为0/1的短多项式），以及大量的“噪声多项式对”（a_i(x), b_i(x)），其中a_i(x)是随机生成的，b_i(x)=-a_i(x)s(x)+e_i(x) (mod q)是通过秘密多项式s(x)计算得到的“响应多项式”，加入噪声e_i(x)是为了让b_i(x)看起来像一个完全随机的多项式，从而隐藏s(x)的存在，而在计算上无法从这些多项式对中恢复出秘密多项式s(x)。对于b_i(x)其生成时每一部分的作用如下：

a_i(x)：从多项式环R_q中均匀随机生成的多项式，相当于“公共输入”，可以公开。

s(x)：秘密多项式（系数仅为0或1），是整个RLWE问题的核心，必须严格保密。

e_i(x)：小系数噪声多项式（系数仅为-1、0、1），是“隐藏秘密”的关键。

b_i(x)：由a_i(x)s(x)加上噪声得到的结果，与ai(x)一起构成公开的“多项式对”。

如果没有噪声e_i(x)，即e_i(x)=0，那么b_i(x)=-a_i(x)s(x) (mod q)，此时攻击者可以通过多组(a_i(x), b_i(x))构建线性方程组，直接解密出秘密多项式s(x)，这就完全失去了安全性。而加入小噪声e_i(x)后：

b_i(x)不再是a_i(x)s(x)的精确结果，而是一个“近似值”；

这个近似值的误差被控制在很小的范围内（由e_i(x)的系数大小决定）；

从计算角度，目前没有任何算法（包括量子算法）能高效地从这些带噪声的近似结果中恢复出s(x)，这正是RLWE问题的“计算困难性”来源，也是BFV适合后量子秘密场景的原因。

1.4 缩放因子

在BFV同态加密方案中，缩放因子（Scaling Factor）是连接明文空间（Z_t）和密文空间（Z_q）的核心系数，本质是为了让明文多项式能“适配”系数模数q的范围，同时保证解密时可以精确还原明文。BFV的明文模数t远小于系数模数q（t<<q)，比如t=65537，q=2⁶⁰量级。

明文多项式m(x)∈R_t的系数范围是[0, t-1]，而密文多项式c(x)∈R_q的系数范围是[0, q-1]，如果直接将明文m(x)放入密文公式，由于t太小，明文信息会被噪声和掩码完全淹没，无法解密。因此需要一个缩放因子，将明文系数放大到q的量级，再参与密文计算。缩放因子贯穿加密和解密两个核心步骤，是明文和密文的“桥梁”。

（1）加密时：明文放大

在加密步骤中，明文多项式m(x)不会直接代入密文公式，而是先乘于缩放因子Δ，再放入到公式：

 

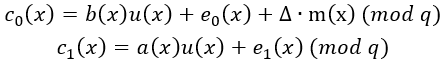
作用：将明文系数从[0, t-1]放大到[0, Δ*(t-1)]，这个范围在q的量级内，能避免明文被噪声覆盖。

（2）解密时：明文缩小

解密的核心步骤是先计算聚合多项式D(ct)，代入加密公式后可得：

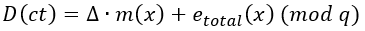
此时需要反向缩放来还原明文：

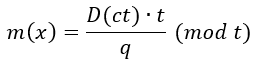
概括来说，缩放因子不会直接参与运算，但会间接影响噪声的增长速度：

1) 加法运算：密文加法是系数直接相加，噪声线性叠加，缩放因子不影响噪声增长；

2) 乘法运算：密文乘法是多项式乘法，噪声会平方增长，而缩放因子Δ越大，噪声的规模也会越大，导致运算深度降低。

因此，在参数配置时，需要在“明文范围（t大小）”和“运算深度（q大小）”之间做权衡：

若t增大→Δ减小→噪声容忍度提升→运算深度增加；

若t减小→Δ增大→噪声容忍度降低→运算深度减小。

所以t与Δ成反比，需根据业务需求平衡明文范围和运算深度。

2 BFV核心流程

2.1 参数配置

参数配置决定方案的性能与安全性，BFV核心参数有4个，需严格满足数学约束：

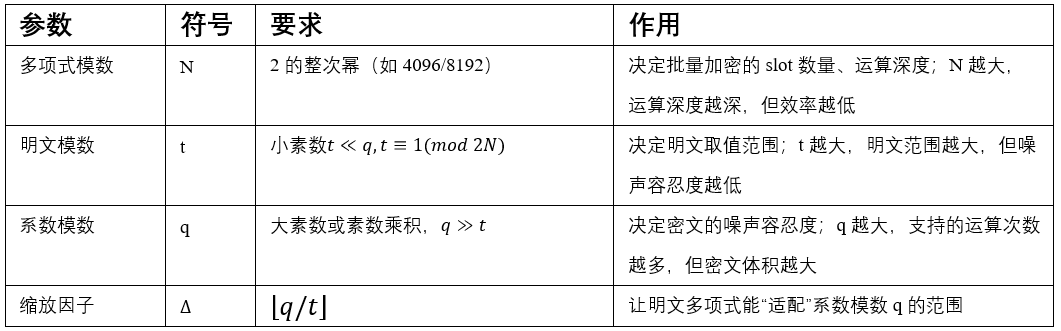
参数约束：需满足q>t*(2N)^d*B（d是目标运算深度，B是噪声上限），否则运算过程中噪声会“爆炸”导致解密失败。

2.2 密钥生成

基于RLWE问题生成私钥、公钥、重线性化密钥3中密钥，核心是构造含噪声的多项式对。

（1）私钥（sk）

随机生成一个短多项式s(x)∈R_q，系数仅为0或1（如s(x) = 1 + x² + x⁵），私钥就是s(x)。

（2）公钥（pk）

随机生成多项式a(x)∈R_q，生成小希数噪声多项式e(x)∈R_q，计算b(x) = -a(x)s(x) + e(x) (mod q)，公钥是多项式对pk = (b(x), a(x))，可公开传播。这里的噪声e(x)让攻击者无法从公钥对中恢复私钥s(x)，目的是解决“公钥本身的安全性”。

（3）重线性化密钥（rlk）

密文乘法会导致密文从“2项多项式”膨胀为“3项多项式”，后续运算效率骤降。重线性化密钥用于将膨胀后的密文压缩回2项，生成逻辑与公钥类似，本质是一组扩展的RLWE多项式对。

2.3 加密

将明文多项式转为密文多项式，BFV的密文是R_q中的2项多项式对ct = (c₀(x), c₁(x))，加密过程分两步：

（1）明文编码：将整数明文m编码为明文多项式m(x)∈R_t；

（2）添加噪声与混淆：

随机生成两个小噪声多项式e₀(x),e₁(x)∈R_q，随机生成一个“掩码多项式”u(x)∈R_q（系数为0/1），计算密文：

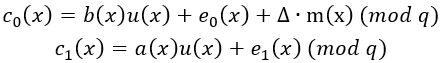
核心设计：密文中包含明文信息m(x)，但被噪声e₀/e₁和掩码u(x)混淆，只有私钥能去除混淆和噪声。该步骤中的掩码多项式u(x)和噪声多项式e₀(x),e₁(x)是两套独立的安全机制，它们解决的是完全不同的问题，不能互相替代，如下图：

u(x)通过随机缩放实现公钥和明文间的非固定线性关系，噪声通过“近似”进一步打破它们之间精确的代数关系，使得攻击者无法从近似值中还原精确明文。

2.4 同态运算

这步的核心是：密文运算=多项式环运算，BFV支持秘密&密文（Ct&Ct）和密文&明文（Ct&Pt）的加减乘运算，所有运算都在多项式环R_q中进行，且无需密钥。

运算后的密文仍然是合法的RLWE密文，可继续参与后续运算——这就是「同态性」的体现。

2.5 解密

解密是加密的逆运算，核心是去除噪声、还原明文多项式，步骤如下：

（1）密文聚合

用私钥s(x)计算聚合多项式：

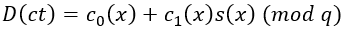
代入加密公式可推导：

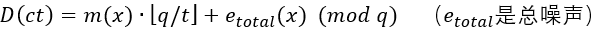
（2）噪声去除

由于总噪声e_total<q/(2t)，可通过“舍入+模运算”还原明文：

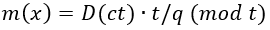（3）明文解码

将解密后的多项式m(x)转换回整数（单整数取常数项，批量加密取所有系数）。

解密成功条件：总噪声e_total<q/(2t)，若运算次数过多导致噪声爆炸，舍入后无法还原明文，则会解密失败——这是BFV“层次性”的本质，运算深度有限。

2.6 python示例

以下是一个完整的python示例程序：

import numpy as np
import random

class PolynomialRing:
    def __init__(self, n, modulus):
        self.n = n
        self.modulus = modulus
        self.phi = np.zeros(n + 1, dtype=int)
        self.phi[0] = 1
        self.phi[n] = 1

    def poly_add(self, a, b):
        result = np.zeros(self.n, dtype=int)
        for i in range(self.n):
            result[i] = (a[i] + b[i]) % self.modulus
        return result

    def poly_mul(self, a, b):
        result = np.zeros(2 * self.n - 1, dtype=int)
        for i in range(self.n):
            for j in range(self.n):
                result[i + j] = (result[i + j] + a[i] * b[j]) % self.modulus
        return self.poly_mod(result)

    def poly_mod(self, poly):
        result = poly.copy()
        for i in range(len(result) - 1, self.n - 1, -1):
            if result[i] != 0:
                coeff = result[i]
                result[i] = 0
                idx = i - self.n
                if idx < len(result):
                    result[idx] = (result[idx] - coeff) % self.modulus
        result = result[:self.n]
        return result

    def poly_sub(self, a, b):
        result = np.zeros(self.n, dtype=int)
        for i in range(self.n):
            result[i] = (a[i] - b[i]) % self.modulus
        return result

    def poly_scale(self, a, scalar):
        result = np.zeros(self.n, dtype=int)
        for i in range(self.n):
            result[i] = (a[i] * scalar) % self.modulus
        return result

    def random_poly(self):
        return np.random.randint(0, self.modulus, self.n)

    def binary_poly(self):
        return np.random.randint(0, 2, self.n)

    def small_poly(self, bound=3):
        return np.random.randint(-bound, bound + 1, self.n)

class BFV:
    def __init__(self, n=256, q=1048576, t=256):
        self.n = n
        self.q = q
        self.t = t
        self.ring = PolynomialRing(n, q)
        self.plaintext_ring = PolynomialRing(n, t)
        self.delta = q // t

    def keygen(self):
        # 产生密钥
        s = self.ring.binary_poly()
        # 挑战多项式
        a = self.ring.random_poly()
        # 随机多项式
        e = self.ring.small_poly()
        a_s = self.ring.poly_mul(a, s)
        # 响应多项式
        pk0 = self.ring.poly_sub(e, a_s)
        # 公钥
        pk = [pk0, a]
        sk = s
        return pk, sk

    # 编码明文
    def encode(self, message):
        if isinstance(message, int):
            # 单整数编码
            m = np.zeros(self.n, dtype=int)
            m[0] = message % self.t
        else:
            # 批量编码
            m = np.array(message, dtype=int) % self.t
        return m

    # 使用公钥加密
    def encrypt(self, pk, message):
        # 对明文进行编码
        m = self.encode(message)
        # 对明文编码结果进行放大
        m_scaled = self.ring.poly_scale(m, self.delta)
        #print("m_scaled: {}".format(m_scaled))
        
        # 生成掩码多项式
        u = self.ring.binary_poly()
        # 产生两个小噪声多项式
        e1 = self.ring.small_poly()
        e2 = self.ring.small_poly()
        
        pk0_u = self.ring.poly_mul(pk[0], u)
        pk1_u = self.ring.poly_mul(pk[1], u)
        
        # 生成密文c0
        c0 = self.ring.poly_add(pk0_u, e1)
        c0 = self.ring.poly_add(c0, m_scaled)
        # 生成密文c1
        c1 = self.ring.poly_add(pk1_u, e2)
        
        # 返回密文
        return [c0, c1]

    def decrypt(self, sk, ciphertext):
        c0, c1 = ciphertext
        s_c1 = self.ring.poly_mul(sk, c1)
        decrypted = self.ring.poly_add(c0, s_c1)
        
        result = np.zeros(self.n, dtype=int)
        for i in range(self.n):
            result[i] = round(decrypted[i] * self.t / self.q) % self.t
        
        return result

    def add(self, c1, c2):
        c0 = self.ring.poly_add(c1[0], c2[0])
        c1 = self.ring.poly_add(c1[1], c2[1])
        return [c0, c1]

def main():
    print("=== BFV 同态加密方案演示 ===\n")
    
    bfv = BFV(n=256, q=1048576, t=256)
    
    print(f"参数设置:")
    print(f"  多项式次数 n = {bfv.n}")
    print(f"  密文模数 q = {bfv.q}")
    print(f"  明文模数 t = {bfv.t}")
    print(f"  缩放因子 Δ = {bfv.delta}\n")
    
    pk, sk = bfv.keygen()
    print("密钥生成完成")
    print(f"私钥 s 前5个系数: {sk[:5]}...\n")
    print(sk)
    
    m1 = 42
    m2 = 17
    print(f"明文 m1 = {m1}")
    print(f"明文 m2 = {m2}\n")
    
    c1 = bfv.encrypt(pk, m1)
    c2 = bfv.encrypt(pk, m2)
    print("加密完成")
    print(f"密文 c1[0] 前5个系数: {c1[0][:5]}...")
    print(f"密文 c1[1] 前5个系数: {c1[1][:5]}...\n")
    print("密文c1 {}".format(c1))
    
    d1 = bfv.decrypt(sk, c1)
    d2 = bfv.decrypt(sk, c2)
    print("解密完成")
    print(f"解密结果 d1 = {d1[0]}")
    print(f"解密结果 d2 = {d2[0]}\n")
    
    print("=== 同态加法演示 ===")
    c_sum = bfv.add(c1, c2)
    d_sum = bfv.decrypt(sk, c_sum)
    expected_sum = (m1 + m2) % bfv.t
    print(f"密文同态加法: c1 + c2")
    print(f"解密结果: {d_sum[0]}")
    print(f"期望结果: {expected_sum}")
    print(f"验证: {'成功' if d_sum[0] == expected_sum else '失败'}\n")
    
    print("=== 多项式明文演示 ===")
    m_poly = np.array([1, 2, 3, 4, 5] + [0] * 251, dtype=int)
    c_poly = bfv.encrypt(pk, m_poly)
    d_poly = bfv.decrypt(sk, c_poly)
    print(f"多项式明文前5个系数: {m_poly[:5]}")
    print(f"解密结果前5个系数: {d_poly[:5]}")
    print(f"验证: {'成功' if np.array_equal(d_poly[:5], m_poly[:5]) else '失败'}")

if __name__ == "__main__":
    main()

3 SEAL使用

3.1 源码编译

这里仅简单介绍下Windows下使用VS2022环境进行编译，下载源码并安装cmake，运行VS2022安装菜单下的“Developer Command Prompt for VS 2022”命令行，执行命令进行配置：

cmake -S . -B build -G "Visual Studio 17 2022" -A x64 -DCMAKE_INSTALL_PREFIX=./out

这里编译的是64位版本，并将安装目录设置为当前目录下的out文件夹，配置完成后再执行以下命令进行编译

cmake --build build --config Release    #编译Release版本
cmake --build build --config Debug      #编译Debug版本

编译完成后会生成seal-4.1.lib库文件：

然后执行以下命令进行安装：

cmake --install build

out下include中是头文件，lib中是静态库文件：

3.2 示例程序

使用VS2022创建空项目，并添加demo.cpp文件，内容如下：

#include <iostream>
#include <SEAL/SEAL.h>

using namespace std;
using namespace seal;

int main() {
    // 步骤 1：配置加密参数（BFV 方案）
    EncryptionParameters parms(scheme_type::bfv);
    // 多项式模数：4096（2的幂次）
    size_t poly_modulus_degree = 4096;
    parms.set_poly_modulus_degree(poly_modulus_degree);
    // 明文模数：支持批量运算，取值范围 2^20
    parms.set_plain_modulus(PlainModulus::Batching(poly_modulus_degree, 20));
    // 系数模数：使用 BFV 默认参数
    parms.set_coeff_modulus(CoeffModulus::BFVDefault(poly_modulus_degree));

    cout << "明文模数 t = " << parms.plain_modulus().value() << endl;
    cout << "明文模数 t 比特数 = " << parms.plain_modulus().bit_count() << endl;
    cout << "t mod 2N = " << (parms.plain_modulus().value() % (2 * poly_modulus_degree)) << endl;

    vector<Modulus> coeff_mods = CoeffModulus::BFVDefault(poly_modulus_degree);

    // 3. 系数模数 q（多素数乘积）
    cout << "\n系数模数 q 的构成（素数列表）：" << endl;
    int total_bits = 0;
    for (size_t i = 0; i < coeff_mods.size(); i++) {
        cout << "第" << i + 1 << "个素数：" << coeff_mods[i].value()
            << "（比特数：" << coeff_mods[i].bit_count() << "）" << endl;
        total_bits += coeff_mods[i].bit_count();
    }
    cout << "系数模数总比特数 = " << total_bits << endl;

    // 步骤 2：创建加密上下文，验证参数合法性
    SEALContext context(parms);
    // 打印上下文信息（可选，查看参数配置）
    cout << "Context created successfully, scheme type: BFV" << endl;

    // 步骤 3：生成密钥（适配 SEAL 4.1 API，核心修改部分）
    KeyGenerator keygen(context);
    // 4.1 版本：通过 create_public_key() 生成公钥（替代原 public_key()）
    PublicKey public_key;
    keygen.create_public_key(public_key);
    // 4.1 版本：直接通过成员函数获取私钥（该接口未变更）
    SecretKey secret_key = keygen.secret_key();
    // 4.1 版本：通过 create_relin_keys() 生成评估密钥（替代原 relin_keys()）
    RelinKeys relin_keys;
    keygen.create_relin_keys(relin_keys);

    // 步骤 4：初始化加密器、解密器、评估器
    Encryptor encryptor(context, public_key);
    Decryptor decryptor(context, secret_key);
    Evaluator evaluator(context);

    // 步骤 5：明文准备（两个整数）
    Plaintext plain1("123");
    Plaintext plain2("456");
    cout << "Original plaintext 1: " << plain1.to_string() << endl;
    cout << "Original plaintext 2: " << plain2.to_string() << endl;

    // 步骤 6：加密明文为密文
    Ciphertext cipher1, cipher2;
    encryptor.encrypt(plain1, cipher1);
    encryptor.encrypt(plain2, cipher2);
    cout << "Plaintext encrypted to ciphertext successfully" << endl;

    // 步骤 7：密文同态运算（加法 + 乘法）
    // 密文加法
    Ciphertext cipher_add;
    evaluator.add(cipher1, cipher2, cipher_add);
    // 密文乘法 + 重线性化（减少密文大小）
    Ciphertext cipher_mult;
    evaluator.multiply(cipher1, cipher2, cipher_mult);
    evaluator.relinearize_inplace(cipher_mult, relin_keys);

    // 步骤 8：解密密文，验证结果
    Plaintext plain_add, plain_mult;
    decryptor.decrypt(cipher_add, plain_add);
    decryptor.decrypt(cipher_mult, plain_mult);
    cout << "Ciphertext add result: " << plain_add.to_string() << endl;
    cout << "Ciphertext multiply result: " << plain_mult.to_string() << endl;
    
    return 0;
}

将之间产生的out文件夹下的include和lib拷贝到项目文件夹下，配置项目的C/C++编译包含头文件路径，库文件路径以及输入库，即可进行编译。

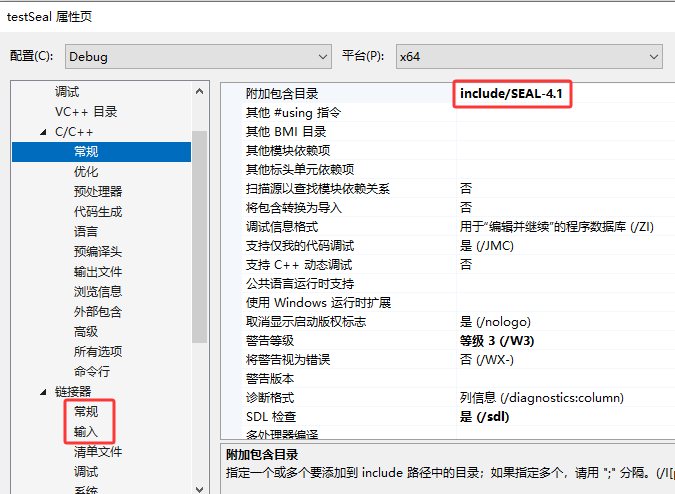
编译完成后运行程序，输出如下：

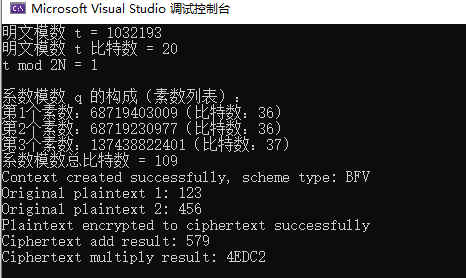
在该示例程序中，多项式模数N是4096，明文模数t是1032193，位宽为20bits，系数模数q是3个素数的乘积68719403009*68719230977*137438822401=0x1ffff4400622fecd904df7f92001，位宽是109bits，示例中演示了0x123和0x456的加法和乘法运行，可见加密运算后的解密结果和未加密运算的结果完全一致。