-
第一次作业:我采用了正则表达式来编写inputhandler,而由于正则表达式不熟练,并且此方法本身难以应对较为复杂的表达式,正则表达式在匹配括号时未采用非贪婪匹配,从而使得匹配错误,如:(...)+(...),此类括号并不会匹配前一个括号而会将整个式子全部匹配从而导致了错误。
-
第二次作业:此次作业我重构了代码,改为用递归下降来实现inputhandler,从而规避了正则表达式。
-
一开始在自定义函数的使用中未考虑到如f(y,x,z)这类参数不按xyz顺序的情况导致了错误。
-
在sum函数中对i的替换后未加上括号,使得形如i**2,等情况下,若i为负得出的结果仍然为负。
-
第三次作业:
-
对sum的start与end未能考虑到int溢出的问题,导致如果数据过大会引发溢出。
-
在互测中,有同学对于三角函数中的表达式判断有误,当三角函数内为单个因子加符号时判断为非表达式,少加了括号。
二、程序结构分析:
-
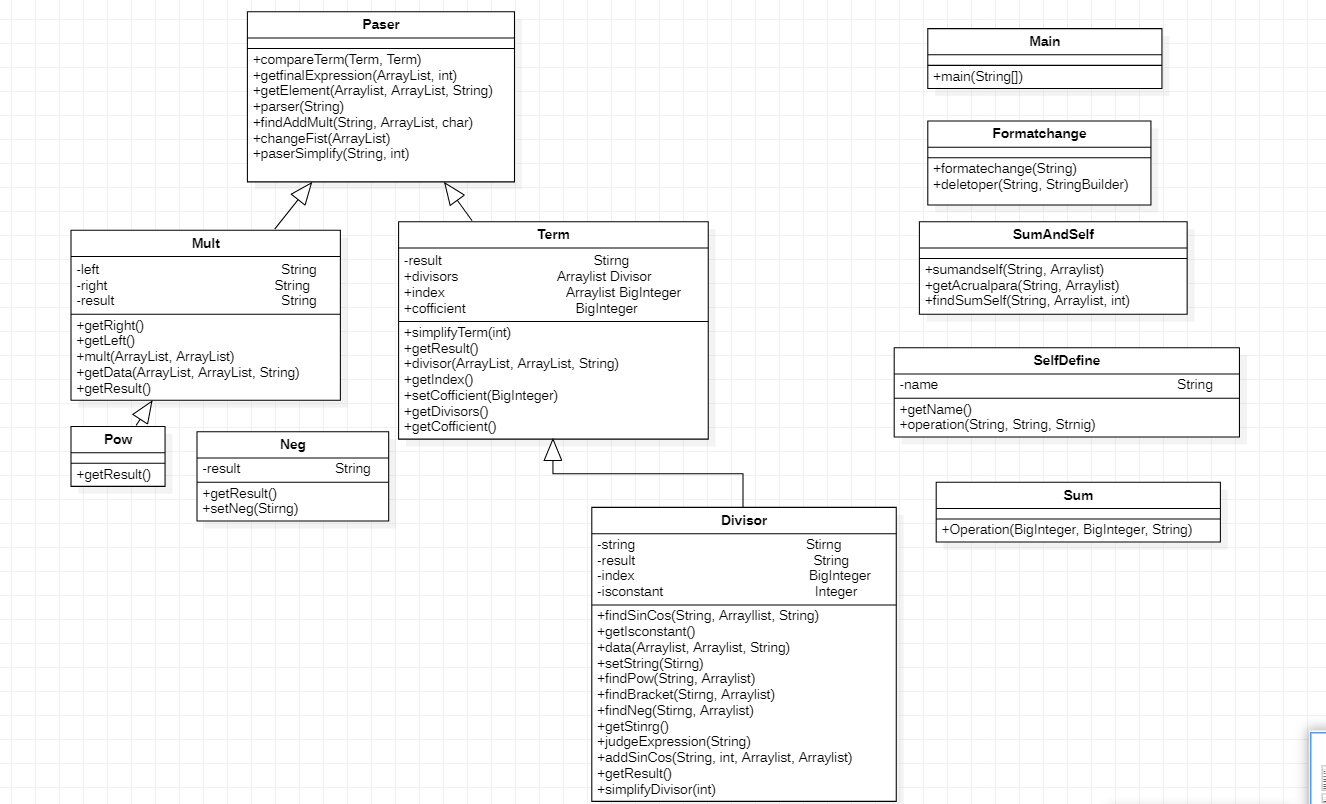
在inputhandler中一共有四个类,用来读入并且提前处理自定义函数和求和函数,这几个类之间没有继承关系只是用来将表达式标准化。
-
其中Formatechenge,SumAndSelf,Sum中只存储函数,输入字符串并且返回处理过的字符串。
-
SelfDefine则是用来存储自定义函数的定义,并且处理表达式中的自定义函数
-
主控阶段分为Paser,Term,Divisor三个类,以括号外的‘+’为界划分项,Term。以括号外‘*’为界划分因子,Divisor。在Divisor中可能出现括号中的表达式因子,此时将该表达式因子当做一个表达式通过递归下降的方法进行展开并化简,即:在重复一遍上述过程。当括号展开后,Term中将包含若干Divisor,通过比较Divisor的底数以及指数来进行合并同类项,然后在Paser中合并Term以完成化简。
在此分析代码中核心的三个类:
-
Divisor:有四个属性,十二个方法
其中分为两部分:
getResult,findNeg,fingdPow,findSinCos,findBracket,用于解析字符串去掉其中的括号。部分代码如下:
if (locatbracket.size() != 0) {
Parser parser = new Parser();
String stringinBracket = string.substring(locatbracket.get(0) + 1, locatbracket.get(1));
data = parser.parser(stringinBracket);
if (locatsin.size() != 0) {
data = "sin(" + data + ")";
}
else if (locatcos.size() != 0) {
data = "cos(" + data + ")";
}
}
else {
data = data(locatneg, locatpow, string);
}
if (locatpow.size() != 0) {
Pow pow = new Pow(data, string.substring(locatpow.get(1) + 1));
data = pow.getResult();
}
if (locatneg.size() != 0) {
Neg neg = new Neg(data);
data = neg.getResult();
}simplifyDivior,addSinCos,getIndex,getIsconstant,judgeExpression用于化简因子同时将因子抽象化为底数和指数,
private Integer isconstant;
private String string;
private BigInteger index;其中addSinCos,judgeExperssion用于判断是否三角函数中为表达式需要多加一层括号。
for (int i = 0; i < expression.length(); i++) {
m = expression.charAt(i);
if (m == '(') {
bracket++;
}
else if (m == ')') {
bracket--;
}
else if (m == '*' && expression.charAt(i - 1) != '*' &&
expression.charAt(i + 1) != '*') {
if (bracket == 0) {
return 1;
}
}
else if (m == '+' && bracket == 0) {
return 1;
}
else if (m == '-' && bracket == 0) {
boolean judge = (expression.charAt(i + 1) < '0' || expression.charAt(i + 1) > '9');
if (i > 0) {
return 1;
}
else if (judge) {
return 1;
}
}
} -
Term:有四个属性,八个方法
同样分为两部分:
getResult,以及从Paser中继承的findAddMult用于解析字符串用‘*’分解项为因子,并且调用所有因子的simplifyDivisor用于化简因子。
for (Divisor divisor : divisors) {
String adivisor = divisor.getResult();
if (flag == 0) {
data = adivisor;
}
else {
data = (new Mult(data, adivisor)).getResult();
}
flag = 1;
}simplifyTerm等方法用于化简Term,通过遍历所有抽象化后的因子,将项抽象化为系数,因子序列。
private ArrayList<Divisor> divisors = new ArrayList<>();
private ArrayList<BigInteger> index = new ArrayList<>();
private BigInteger cofficient = new BigInteger("1");同时底数相同的因子可以进行指数相加用来合并同类项。
for (int i = 0; i < divisors.size(); i++) {
divisori = divisors.get(i);
if (divisori.getIsconstant() == 1) {
cofficient = cofficient.multiply(new BigInteger(divisori.getString()));
divisors.remove(i);
index.remove(i);
i--;
}
else {
for (int j = i + 1; j < divisors.size(); j++) {
divisorj = divisors.get(j);
if (divisori.getString().equals(divisorj.getString())) {
index.set(i, index.get(i).add(index.get(j)));
divisors.remove(j);
index.remove(j);
j--;
}
}
}
} -
Paser:七个方法
分为两个部分:
parser,findAddMult,getElement,用来解析表达式,以’+‘为基准将表达式变为项,同时调用Term的去括号和化简方法。
paserSimplify,getfinalExpression,changeFirst,compareTerm用于合并相同的Term,在输出时如果遇到系数为0的Term则不输出,同时如果最终输出为空串则将输出0。
for (int i = 0; i < terms.size(); i++) {
termi = terms.get(i);
for (int j = i + 1; j < terms.size(); j++) {
termj = terms.get(j);
if (compareTerm(termi, termj)) {
BigInteger op1;
BigInteger op2;
op1 = terms.get(i).getCofficient();
op2 = terms.get(j).getCofficient();
op1 = op1.add(op2);
terms.get(i).setCofficient(op1);
terms.remove(j);
j--;
}
}
}
//输出
return getfinalExpression(terms, type); -
由于乘法在运算中相对特殊,所以乘法和乘方单独构造了一个类用以实现,同时需要用到Paser中的findAddMult方法以’+‘为基准切分表达式为项。
-
在此设计中类之间的耦合程度并不高,表达式,项,因子都相对独立,并且都基本分为去括号,化简两个阶段,只有findAddMult方法在Paser,Term,Mult类共同使用。
-
内聚性有待提高,在Paser,Term,Divisor中有较多的调用彼此的方法。
-
从整体上看,由于我采用了先去括号再化简的思路,整个处理分为两个阶段,在两个阶段中单独的代码都较为简单且易实现。但在去括号阶段仍然对于字符串的直接操作比较多,在抽象化上做的并不好。在Divisor中我只是简单的将因子抽象为底数和指数,在可扩展性中有一些不足,比如如果表达式中存在x以外的变量,那么在化简过程中可能会产生问题。
程序复杂度分析:
-
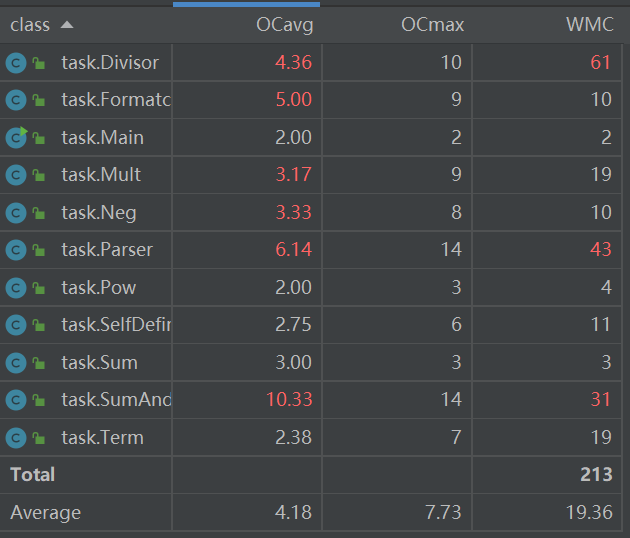
由于在字符串的解析化简的过程中使用了双重循环所以Formatechange,SumAndSelf,Mult,Neg的复杂度较高。
-
而在进行去括号并抽象化,以及进行化简的过程中,由于括号内的表达式化简以及三角函数内表达式化简使用了递归调用,所以复杂度较够,这涉及到了Divisor,Paser。
-
对于复杂度过大的问题在编写代码的过程中也有所考虑,仅仅在遇到括号时才递归。但个人没有找到不进行递归的较好思路。
三、一些bug:
-
在第一次作业中由于对形式化表达理解不够出现了*-x的结构,这样显然不符合形式化表达
-
在第三次作业对sum的start与end未能考虑到int溢出的问题,导致如果数据过大会引发溢出。
四、发现别人bug的策略:
-
将自己之前出现的bug来测试别人的代码
-
通过读他人的代码来发现bug
-
测试边界数据及特殊情况,如:sum中start>end的情况
五、架构设计体验:
在三次作业中,第一次作业对表达式的解析采用了正则表达式的方法,去括号及化解使用的是二叉树的方式,将整个表达式变成二叉树再遍历二叉树。
第二次作业因为杂度的提升,正则表达式无法进行解析,从而采用了递归下降的解析方法。
第三次作业由于多层括号可能出现,可能导致递归过深,所以修改了结构,使得解析表达式时只有遇到括号时才会递归,从而使得程序运行时间不会过长。同时由于采用先去括号再化简,可能会导致表达式过长而内存溢出,所以在每次乘法操作后进行了一次小的化简,保证不会溢出。
六、心得体会:
在这三次作业中,从第一次作业时的一头雾水,到第三次作业相对的顺利,其中经历了许多次重构,才找到一种较为合适的设计。在OO的学习中,我感觉到并没有设计的标准答案,更多的是在自己的探索中不断寻找更优解的一个过程。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号