汉诺塔问题

  通过几日的查资料，汉诺塔问题终于有了些头绪，在这里将近日的成果整理一下，也为各位朋友提供一些参考资料。

  汉诺塔问题想必大家都知道，先给出图

  

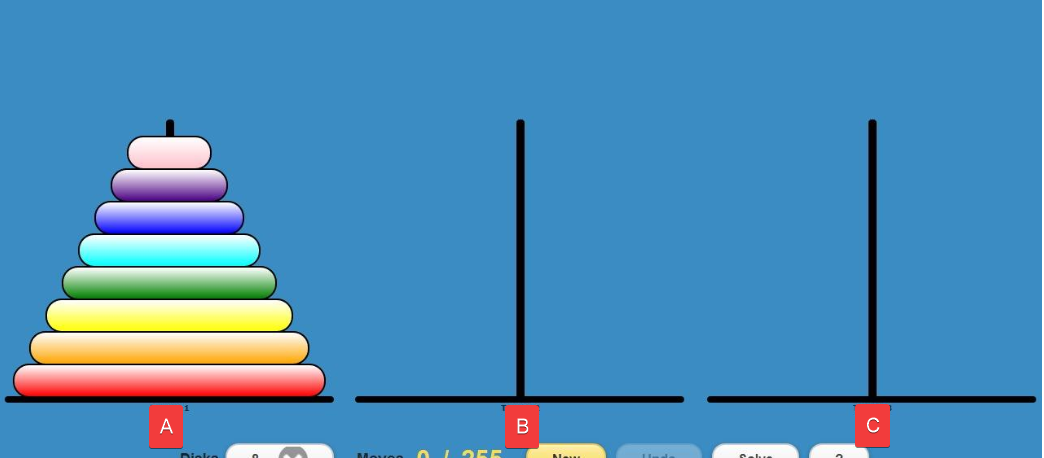
  就是将图中A柱中的圆盘，通过B柱当辅助，一次移动一个，并且时刻保持大盘在上小盘在下，全部移动到C柱。

  假设有A柱有N个圆盘，通过B柱移动到C柱。用数学中递归的思想来解决这个问题，先将N-1个移动到B柱，再将第N个移动到C柱，最后将N-1个移动到C柱。大功告成，继续，那么解决N-1个的问题，先将N-2个移动到A柱，再将第N-1个移动到C柱，最后将N-2个移动到C柱。再解决N-2个的问题，先将N-3个移动到B柱，再将第N-2个移动到C柱，最后将N-3个移动到C柱。以此往下，就可以移完，但移动的过程中有一个规律，就是在不停的变换起使柱和辅助柱，当N-1个移动到B柱时，辅助柱是C柱，当N-2个移动到A柱时辅助柱是B柱，当N-3个移动到B柱时辅助柱是C柱。通过这种规律，编写JAVA代码

public class Exercise2 {

    public static void main(String[] args) {

        char a = 'A';
        char b = 'B';
        char c = 'C';

        //从键盘输入n
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        hanoi(n, a, b, c);

    }

    public static void hanoi(int n, char a, char b, char c) {

        //如果只有一个圆盘，则直接将圆盘从A柱移动到B柱
        if(n == 1) {
            System.out.println("Disk 1 from " + a + " to " + c);

        }else {

            //先将n-1个圆盘从A柱通过C柱移动到B柱
            hanoi(n-1, a, c, b);
            System.out.println("Disk " + n + " from " + a + " to " + c);

            //再将n-1个圆盘从B柱通过A柱移动到C柱
            hanoi(n-1, b, a, c);
        }
    }

}

通过方法的自我调用，实现递归，而在JAVA代码中改变的就是起使柱和辅助柱的参数序列。

这就是我大概的解题思路了，不足指出还望各位朋友多多指正。