折半插入排序

点击查看代码

/*折半插入排序
假设待排序数组为a[len]，初始时默认a[0]为有序区，a[1]~a[len-1]为无序区
i是无序区索引，j是有序区索引，tmp暂存无序区待插入元素（避免有序区元素后移时覆盖掉）
如果要按降序排序，则将判断语句改为if (a[mid] < tmp) //大于a[mid]的关键字排在左边，小于等于的排在右边
*/
#include <iostream>
using namespace std;

/*
函数功能：折半插入排序（升序排序）
函数列表：
a[]：待排序数组
n：待排序元素个数
*/
void BinInsertSortUp(int a[], int n){
	int i, j, tmp;
	//默认a[0]为有序区，因此无序区元素范围是[1,n-1]
	for (i = 1; i < n; i++) {  		
		tmp = a[i]; //暂存无序区待插入元素（同时也是本轮排序的比较基准）
		int left = 0, right = i - 1; //折半查找范围[left,right]即有序区范围[0,i-1]

		//对有序区进行折半查找，当左或右边界超出范围时退出
		while (left <= right) {	  		
			//int mid = (left + right);//求中点mid，如果left + right相加大于int的最大值会发生溢出
			int mid = left + ((right - left) >> 1); //用right - left，然后右移1位当作除以2可以保证不溢出		
			if (a[mid] > tmp) {
				right = mid - 1; //小于a[mid]的元素插在左边，折半查找范围改为[left,mid-1]，mid已经判断，不用包含mid
			}		
			else { 
				left = mid + 1; //大于等于a[mid]的元素插在右边，折半查找范围改为[mid+1,right]。相等的元素不改变相对位置，属于稳定算法
			}
		}

		//找到插入位置left后，要先将[left, i-1]区间内的元素各后移一位，然后才能将tmp插到a[left]中
		//从后往前移可以避免覆盖前面的元素
		for (j = i - 1; j >= left; j--) {
			a[j + 1] = a[j];
		}
		a[left] = tmp; //最后将tmp插到a[left]中
	}	
}	

int main(){
	int a[] = {8,7,6,5,4,3,2,1,0};//待排序列
	int n = sizeof(a) / sizeof(a[0]);
	cout << "序列个数：" << n << endl;
	cout << "排序前：";
	for (int i = 0; i < n; i++) {
		cout << a[i] << " ";
	}
	cout << endl;
	BinInsertSortUp(a, n); //折半插入排序
	cout << "排序后：";
	for (int i = 0; i < n; i++) {
		cout << a[i] << " ";
	}
	cout << endl;
	return 0;
}

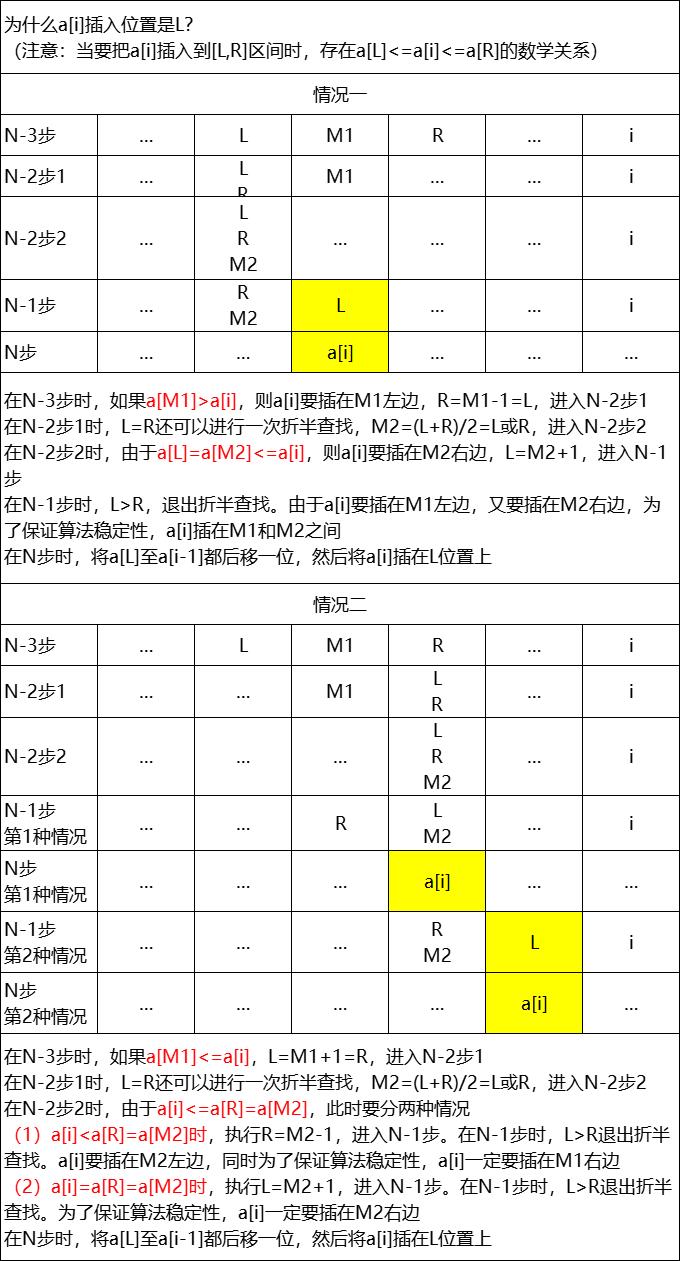
# 折半插入排序位置确定解释