AtCoder Beginner Contest 247 F - Cards

Cards

给定\(n\)张牌\((1≤N≤2×10^5)\)，其正面为数字\(P_i\)，反面为\(Q_i\)，\(1≤P_i,Q_i≤N\)，其中\(P=(P_1,\ldots,P_N)\)，\(Q=(Q_1,\ldots,Q_N)\)都是由\((1, 2, \dots, N)\)构成的序列。请问有多少种选取方式，使得正面和反面的数字包含\((1,2……,N)\)。

由于可能数量很多，所以请对\(1e9+7\)取模。

输入格式

第一行输入\(N\)。

第二行输入\(n\)个数字，为序列P；

第三行输入\(n\)个数字，为序列Q；

输出格式

输出一个数字，为对\(1e9+7\)取模后的可能数。

题目解析

问题转换：从卡牌变成环

如果将每张卡牌看做是连接\(p_i\)和\(q_i\)的边，将每个数字看作点，本题就转换为求取选取边后，包含了所有点的方法数。

由于序列\(P,Q\)包含\(1,2...N\)一次，因此每个点都有且只有一次入度、一次出度，所以最终得到的图一定可以变成若干个环（包含自环），且环的长度合为\(n\)（假设自环的长度为\(1\)）。环的长度可以用并查集、深搜所得，在这里不多加赘述。

对于每个环而言，其能贡献的答案数量只与其长度有关，而对于所有环而言，答案就是每个环贡献数量的乘积（即为乘法原理）。因此，我们假设：\(f[i]\)为长度为\(i\)的环选取若干条边能得到所有点的方法数量，下面开始探究\(f[i]\)如何得到。

环

在探究\(f[i]\)是如何结果之前，我们先再确定一下我们的目标：在有\(i\)个点的环中，选取若干条边，使得所有点都被选取的方法数量。

只有一个点的话，就只有自环，所以只能选取那一条边，\(f[1]=1\)。

如果两个点的话，看似是可以选择一条边，但是结合题意，这实际上需要两张牌，实际上有两条边，我们既可以二选一，又可以两条边都选，一共三种选取方法，\(f[2]=3\)。

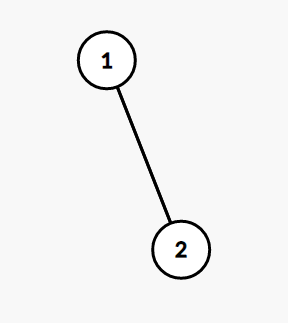
有三条点，至少选择两条边才能包含所有点，选择2条边存在3种选法，选择3条边存在1中选法，\(f[3]=4\)。

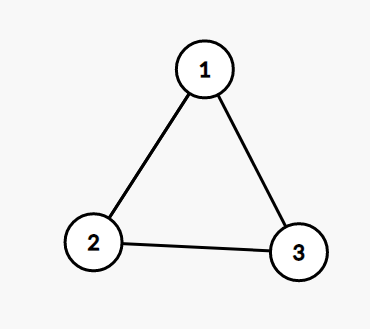
存在4个点，如果选取两条边，可以选取（1-2，3-4）、（1-4，2-3），如果选取三条边，可以选取（1-2，2-3，3-4），（1-2，2-3，4-1），（1-2，3-4，4-1），（2-3，3-4，4-1），如果选取四条边，可以选取（1-2，2-3，3-4，4-1）。一共7中选取方法，\(f[4]=7\)。

我们得到：

• \(f[1] = 1\)
• \(f[2]=3\)
• \(f[3]=4\)
• \(f[4]=7\)
• ……

到这里，我们不妨大胆的猜测，\(f[i]=f[i-1]+f[i-2],且f[0]=2,f[1]=1\)。

事实上，这确实是对的，\(f\)满足卢卡斯序列的递推性质。下面让我们想想这该如何证明。

证明：环与链

当我们想对环进行证明的时候，我们完全可以先把环退化成一条链，现在我们先把环去掉一个点进行探讨：

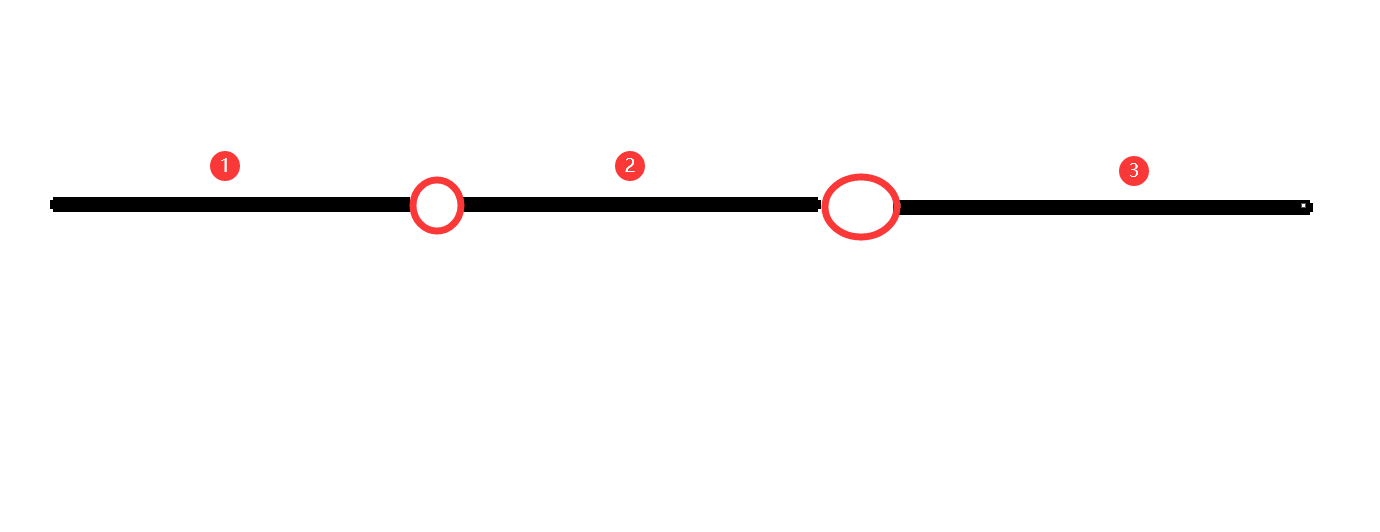
假设\(g[i]\)为长度为\(i\)的链，通过选边覆盖所有点的方法数。

为了选上所有的点，相邻的边至少要选择一条，如果选择边\(1\)的话，那么边\(2\)可以选或者不选，即为\(g[i-1]\)，如果不选择边\(1\)，则必须选择边\(2\)，即为\(g[i-2]\)。

因此可得：

\[g[i]=g[i-1]+g[i-2] \]

现在再回到链的情况，无非便是末尾加个点

如果选择边\(1\)，则剩下情况与\(g[i-1]\)一致，如果不选择边\(1\)，为了选中所有的点，我们必选与\(1\)相邻的两条边，剩下的情况与\(g[i-3]\)一致。

因此，我们可以得到：

\[f[i]=g[i-1]+g[i-3] \]

由于：

\[\begin{align*} g[i]&= g[i-1]-g[i-2]\\ \end{align*} \]

可得：

\[\begin{align*} f[i]&=g[i-1]+g[i-3]\\ &=g[i-2]+g[i-3]+g[i-4]+g[i-5]\\ &=f[i-1]+f[i-2] \end{align*} \]

AC Code

//Cards
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 7, M = 998244353;
int n, p[N], h[N], cnt, ans, l[N] = {0, 1, 3};
bool vis[N];
int dfs(int k) {
	if (l[k]) return l[k];
	return l[k] = (dfs(k-1)+dfs(k-2)) % M;
}
int main(){
	scanf ("%d", &n);
	for (int i = 1; i <= n; i++) scanf ("%d", p + i);
	for (int i = 1, x; i <= n; i++) {
		scanf ("%d", &x);
		h[p[i]] = x;
	}
	long long ans = 1;
	for (int i = 1; i <= n; ++i) {
		if (vis[i]) continue;
		int cnt = 0;
		int t = h[i];
		while (!vis[t]) vis[t] = true, t = h[t], ++cnt;
		dfs(cnt);
		ans = ans * l[cnt] % M;
	}
	printf("%lld", ans);
	return 0;
}