莫比乌斯反演
一、先补充几个常用和式规则
二、积性函数的概念
如果 \(a,b\) 互素,\(f(ab)\) = \(f(a)\) \(*\) \(f(b)\) ,就称 \(f\) 为积性函数
如果 \(p\) 为素数,并且 \(f(p^n) = f^n(p)\) 则f为完全积性函数
三、狄利克雷卷积
定义:设 \(f\), \(g\) 是算数函数,记 \(f\) 和 \(g\) 的狄利克雷卷积是 \(f * g\) , 定义为:
四、莫比乌斯函数的概念
反演原理:
证明如下:
第二个式子的证明和第一个基本一致
同时莫比乌斯函数还有另外一个性质
这个反演法则对所有满足 \(\sum_{k,d\geq1}|f(x/kd)| < \infin\)
证明如下:先假设 \(g(x)=\sum_{d\geq1}f(x/d)\) ,那么
五、整除分块(数论分块)
循环遍历求当然可以,但是如果 \(n\) 很大,并且配合其它的式子求解的话,时间复杂度就会非常高
首先我们想一下,对于每一个 \(i\) 都是 \(n/i\)的下取整,这个有什么性质呢
比如 \(n / i\)的下取整得到了一个 \(k\),那么这个 \(i\) 一定小于等于 \(n/k\), 这也就是说从 \(i\) 到 \(n/k\)得到的答案一定都是 \(k\)
代码如下:
for(int i = 1; i <= n; ) {
int r = n / (n / i);
sum2 += (n / i) * (r - i + 1);
i = r + 1;
}
六、例题
1.\(P3455 [POI2007]ZAP-Queries\)
题目描述
密码学家正在尝试破解一种叫 \(BSA\) 的密码。
他发现,在破解一条消息的同时,他还需要回答这样一种问题:
给出 \(a, b, d\),求满足 \(1 \leq x \leq a\),\(1 \leq y \leq b\)且 \(gcd(x, y) = d\) 的二元组的数量。
因为要解决的问题实在太多了,他便过来寻求你的帮助。
输入格式
输入第一行一个整数 nn,代表要回答的问题个数。
接下来 \(n\) 行,每行三个整数 \(a, b, d\)。
输出格式
对于每组询问,输出一个整数代表答案。
输入 #1
2
4 5 2
6 4 3
输出 #1
3
2
说明
对于全部的测试点,保证 \(1 \leq n \leq 5 * 10^4\), \(1 \leq d \leq a\), \(b \leq 5 * 10^4\)。
解题思路:
然后利用数论分块的知识就可以AC了
链接:https://www.luogu.com.cn/problem/P3455
AC代码
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10;
bool vis[N];
int prime[N], mu[N], cnt, sum[N];
void getMu() {
mu[1] = 1;
for(int i = 2; i < N - 1; i++) {
if(!vis[i]) {
prime[cnt++] = i;
mu[i] = -1;
}
for(int j = 0; j < cnt && i * prime[j] < N - 1; j++) {
vis[i * prime[j]] = 1;
mu[i * prime[j]] = -mu[i];
if(i % prime[j] == 0) {
mu[i * prime[j]] = 0;
break;
}
}
}
for(int i = 1; i < N - 1; i++) {
sum[i] = sum[i - 1] + mu[i];
}
}
void solve(int a, int b, int d) {
int ans = 0;
a /= d; b/= d;
int ed = min(a, b);
for(int i = 1; i <= ed; ) {
int r1 = a / (a / i);
int r2 = b / (b / i);
int r = min(r1, r2);
ans += (sum[r] - sum[i - 1]) * (a / i) * (b / i);
i = r + 1;
}
printf("%d\n", ans);
}
int main() {
getMu();
int t, a, b, d;
scanf("%d", &t);
while(t--) {
scanf("%d%d%d", &a, &b, &d);
solve(a, b, d);
}
return 0;
}
2.\(YY的GCD\)
题目描述
神犇 \(YY\) 虐完数论后给某某出了一题
给定 \(N,M\),求 \(1 \leq x \leq N, 1 \leq y \leq M\) 且 \(gcd(x,y)\) 为质数的 \((x, y)\) 有多少对。
输入格式
第一行一个整数 \(T\) 表述数据组数。
接下来 \(T\) 行,每行两个正整数 \(N, M\)。
输出格式
\(T\) 行,每行一个整数表示第 \(i\) 组数据的结果。
输入输出样例
输入#1
2
10 10
100 100
输出#1
30
2791
说明/提示
\(T = 10^4\), \(N,M \leq 10^7\)
解题思路:
如果只是化到这里,就算用数论分块也是过不了,也会t掉
仔细看下就会发现,可以令 \(T = pd\),原式就可以变为
可以看出来后面的那个和式是可以预处理的
链接:https://www.luogu.com.cn/problem/P3455
AC代码:
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 1e7 + 10;
const int maxx = 1e7 + 1;
bool vis[N];
int mu[N], prime[N], cnt, sum[N];
void getMu() {
mu[1] = 1;
for(int i = 2; i < maxx; i++) {
if(!vis[i]) {
prime[cnt++] = i;
mu[i] = -1;
}
for(int j = 0; j < cnt && i * prime[j] < maxx; j++) {
vis[i * prime[j]] = 1;
mu[i * prime[j]] = -mu[i];
if(i % prime[j] == 0) {
mu[i * prime[j]] = 0;
break;
}
}
}
for(int i = 0; i < cnt; i++) {
for(int j = 1; j * prime[i] < maxx; j++) {
sum[prime[i] * j] += mu[j];
}
}
for(int i = 1; i < maxx; i++) {
sum[i] += sum[i - 1];
}
}
void solve(int n, int m) {
long long ans = 0;
for(int i = 1; i <= min(n, m); ) {
int r = min(n / (n / i), m / (m / i));
ans += 1ll * (sum[r] - sum[i - 1]) * (n / i) * (m / i);
i = r + 1;
}
printf("%lld\n", ans);
}
int main() {
getMu();
int n, m;
int t;
scanf("%d", &t);
while(t--) {
scanf("%d%d", &n, &m);
solve(n, m);
}
return 0;
}
3.最小公倍数之和
题目描述
对于 \(A_1, A_2, ..., A_N\),求
\(\sum_{i = 1}^N\sum_{j = 1}^Nlcm(A_i,A_j)\)的值。
\(lcm(a,b)\) 表示 \(a\) 和 \(b\) 的最小公倍数
输入格式
第一行,一个整数 \(N\)。
第二行, \(N\) 个整数 \(A_1, A_2, ..., A_N\)。
输出格式
一个整数,表示所求的值。
输入输出样例
输入#1
2
2 3
输出#1
17
说明/提示
对于 \(30\%\) 的数据, \(1 \leq N \leq 1000\); \(1 \leq A_i \leq 50000\);
对于另外 \(30\%\) 的数据, \(1 \leq N \leq 50000\); \(1 \leq A_i \leq 1000\);
对于 \(100\%\) 的数据, \(1 \leq N \leq 50000\); \(1 \leq A_i \leq 50000\)。
解题思路:
写到这发现如果艾弗森表达式写成 \([gcd(A_i/k, A_j/k) == 1]\),前面的 \(i,j\)范围没办法缩,因为 \(A_i \neq i\),
所以我们转化下思路,怎么让 \(i\) 表示 \(A_i\)呢?如果我们记录 \(A_i\) 的最大值 \(n\),然后再用一个数组,比如说
\(C_i\)来记录每一个 \(A_i\) 出现的次数,然后就可以写成:
链接:https://www.luogu.com.cn/problem/P3911
AC代码:
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10;
bool vis[N];
int prime[N], cnt, mu[N], sum[N], x, maxx = 0, s[N];
void getMu() {
mu[1] = 1;
for(int i = 2; i < N; i++) {
if(!vis[i]) {
prime[cnt++] = i;
mu[i] = -1;
}
for(int j = 0; j < cnt && i * prime[j] < N; j++) {
vis[i * prime[j]] = 1;
mu[i * prime[j]] = -mu[i];
if(i % prime[j] == 0) {
mu[i * prime[j]] = 0;
break;
}
}
}
for(int i = 1; i < N; i++) {
for(int j = 1; j * i < N; j++) {
sum[i * j] += mu[i] * i;
}
}
}
void solve() {
long long ans = 0;
for(int T = 1; T <= maxx; T++) {
long long sumt = 0;
for(int i = 1; i <= maxx / T; i++) {
sumt += 1ll * i * s[i * T];
}
ans += 1ll * T * sumt * sumt * sum[T];
}
printf("%lld\n", ans);
}
.
int main() {
getMu();
int n;
scanf("%d", &n);
for(int i = 0; i < n; i++) {
scanf("%d", &x);
maxx = max(maxx, x);
s[x]++;
}
solve();
return 0;
}
4.能量采集
题目描述
栋栋有一块长方形的地,他在地上种了一种能量植物,这种植物可以采集太阳光的能量。在这些植物采集能量后,栋栋再使用一个能量汇集机器把这些植物采集到的能量汇集到一起。
栋栋的植物种得非常整齐,一共有 \(n\) 列,每列有 \(m\) 棵,植物的横竖间距都一样,因此对于每一棵植物,栋栋可以用一个坐标 \((x,y)\) 来表示,其中 xx 的范围是 \(1\) 至 \(n\) ,\(y\) 的范围是 \(1\) 至 \(m\) ,表示是在第 \(x\) 列的第 \(y\) 棵。
由于能量汇集机器较大,不便移动,栋栋将它放在了一个角上,坐标正好是 \((0,0)\)。
能量汇集机器在汇集的过程中有一定的能量损失。如果一棵植物与能量汇集机器连接而成的线段上有 \(k\) 棵植物,则能量的损失为 \(2k+1\)。例如,当能量汇集机器收集坐标为 \((2,4)\) 的植物时,由于连接线段上存在一棵植物 \((1,2)\) ,会产生 \(3\) 的能量损失。注意,如果一棵植物与能量汇集机器连接的线段上没有植物,则能量损失为 \(1\) 。现在要计算总的能量损失。
下面给出了一个能量采集的例子,其中 \(n=5\) ,\(m = 4\),一共有 \(20\) 棵植物,在每棵植物上标明了能量汇集机器收集它的能量时产生的能量损失。
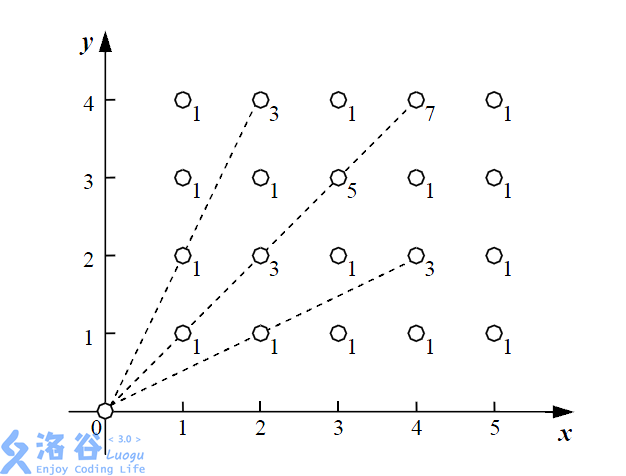
在这个例子中,总共产生了 \(36\) 的能量损失。
输入格式
一行两个整数 \(n,m\)。
输出格式
仅包含一个整数,表示总共产生的能量损失。
输入输出样例
输入#1
5 4
输出 #1
3 6
输入#2
3 4
输出#2
20
说明/提示
\(1 \leq n,m \leq 10^5\)
解题思路:
不难发现从 \((0,0)\) 到 \((x,y)\) 的一条线上不算上这两个点一共有 \(gcd(x,y) - 1\) 个点
所以可以列个式子:
所以这题就相当于求解这个和式
链接:https://www.luogu.com.cn/problem/P1447
AC代码:
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 1e6 + 10;
bool vis[N];
int prime[N], cnt, mu[N], sum[N];
void getMu() {
mu[1] = 1;
for(int i = 2; i < N; i++) {
if(!vis[i]) {
prime[cnt++] = i;
mu[i] = -1;
}
for(int j = 0; j < cnt && i * prime[j] < N; j++) {
vis[i * prime[j]] = 1;
mu[i * prime[j]] = -mu[i];
if(i % prime[j] == 0) {
mu[i * prime[j]] = 0;
break;
}
}
}
for(int i = 1; i < N; i++) {
for(int j = 1; j * i < N; j++) {
sum[i * j] += mu[j] * i;
}
}
for(int i = 1; i < N; i++) {
sum[i] += sum[i - 1];
}
}
void solve(int n, int m) {
long long ans = 0;
for(int i = 1; i <= min(n, m); ) {
int r = min(n / (n / i), m / (m / i));
ans += 1ll * (sum[r] - sum[i - 1]) * (n / i) * (m / i);
i = r + 1;
}
printf("%lld\n", 2 * ans - 1ll * n * m);
}
int main() {
getMu();
int n, m;
scanf("%d%d", &n, &m);
solve(n, m);
return 0;
}
这样处理后面那个和式是可以过的,但是这题还可以再优化一下
首先 \(\sum_{d|m} \varphi(d)=m \Leftarrow \Rightarrow \varphi(m)=\sum_{d|m}\mu(d){m \over d}\)
然后发现后面那个要预处理的和式转换一下就等于 \(\varphi(T)\) ,所以只要在素数筛里求 \(\varphi(T)\)就可以
再补充一下欧拉函数的知识(\(p\) 代表素数)
如果 \(n = p_1^{k_1}*p_2^{k_2}*...*p_m^{k_m}\) ,那么 \(\varphi(n) = \varphi(p_1^{k_1})*\varphi(p_2^{k_2})*...*\varphi(p_m^{k_m})\), 因为欧拉函数是积性函数
还有 \(\varphi(p^k) = p^k-p^{k-1}\)
所以
所以如果 \(p\) 是素数,并且 \(p\) 是 \(x\) 的因子
如果 \(p\) 不是 \(x\) 的因子, 那么 \(p\) 和 \(x\) 互素,则
AC代码:
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N = 1e6 + 10;
bool vis[N];
int prime[N], cnt, mu[N];
ll sum[N], phi[N];
void getMu() {
phi[1] = sum[1] = 1;
for(int i = 2; i < N; i++) {
if(!vis[i]) {
prime[cnt++] = i;
phi[i] = i - 1;
}
for(int j = 0; j < cnt && i * prime[j] < N; j++) {
vis[i * prime[j]] = 1;
if(i % prime[j] == 0) {
phi[prime[j] * i] = phi[i] * prime[j];
break;
}
phi[prime[j] * i] = phi[prime[j]] * phi[i];
}
sum[i] = sum[i - 1] + phi[i];
}
}
void solve(int n, int m) {
ll ans = 0;
for(int i = 1; i <= min(n, m); ) {
int r = min(n / (n / i), m / (m / i));
ans += 1ll * (sum[r] - sum[i - 1]) * (n / i) * (m / i);
i = r + 1;
}
printf("%lld\n", 2 * ans - 1ll * n * m);
}
int main() {
getMu();
int n, m;
scanf("%d%d", &n, &m);
solve(n, m);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号