2021级新生个人训练赛第11场
2021级新生个人训练赛第11场
问题 A: 水下机器人
题目描述
潜水机器人潜入水深h米的湖中进行水下作业,从它在水中的位置到水面的距离为它的水下深度。机器人最初的水下深度为s米,当它不再水面(水下深度>0)时,一个u指令可使它上浮1米;当它不再湖底(水下深度<h)时,d指令可使它下沉1米。但它在水面时,u指令时无效的;在湖底时,d指令时无效的。
现给出一个指令序列(其中包含u或d字符),请你求出执行完整个指令序列后,机器人的水下深度。
输入
第一行依次为h和s。0<=s,s<=h,但0<h<100。
第二行是一个长度不超过100的指令字符串。
输出
只有一个数, 就是机器人最后的水下深度。
样例输入
9 1
uduudd
样例输出
2
解题思路
模拟潜艇的位置s,s小于等于0了不能向上了,s大于等于深度h就不能向下了。最后输出s即可
#include<cstdio>
int main() {
int h,s;
scanf("%d%d",&h,&s);
char ch[200];
scanf("%s",ch+1);
for(int i = 1 ; ch[i] ; i++) {
switch(ch[i]){
case 'u':
if(s<=0)
continue;
s--;
break;
case 'd':
if(s>=h)
continue;
s++;
break;
}
}
printf("%d",s);
}
问题 B: 线段覆盖II
题目描述
输入n个小于10^8且互不相等的正整数,对应数轴上n个点,允许你用m条线短把所有点覆盖,求覆盖住所有点的m条线段的总长度最少是多少?请注意:仅覆盖一个点的线段的长度可看成0,线段的端点视为被覆盖。
输入
第一行依次为n和m,0<m<=n。第二行有n个小于10^8的正整数。
对于80%的数据n<5000;对于100%的数据n<500000。
输出
只有一个数,就是m条线段的最小长度和。
样例输入
3 2
5 1 8
样例输出
3
解题思路
使用贪心的思想。
-
假设我们有n段线条,那么我们所需线段和是0,即每个点都被一段线条覆盖。
-
我们每少一条线段,就需要找到一条两点之间最短的距离,然后合成一条线段。
也就是说,我们有m段线条的话,就需要计算前n-m条最短的两点距离和,现在我们面临的问题是得到排序过的两点距离:
- 在读入点的坐标之后,我们先把点进行从小到大的排序,然后计算每个点与它后面的点的距离dis(distance),得到dis数组后,再把dis进行从小到大的排序。
值得注意的是,n的取值范围为500000,如果使用冒泡排序、选择排序、插入排序这种时间复杂度为\(O(n^2)\)的排序方法,是大概率超时的,这里我们没有时间介绍快速排序方法了,所以使用algorithm库里的sort函数,其时间复杂度是\(O(nlogn)\)可以保证在时间范围内,sort函数使用方法请看这里。
在代码中,由于需要读入的数据量较大,为了提速我也写了一份快读,有兴趣的同学请看这里。
#include<cstdio>
#include<algorithm>
using namespace std;
inline int read() {
int X=0;
bool flag=1;
char ch=getchar();
while(ch<'0'||ch>'9') {
if(ch=='-') flag=0;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
X=(X<<1)+(X<<3)+ch-'0';
ch=getchar();
}
if(flag) return X;
return ~(X-1);
}
int a[550000];
int dis[550000];
int n,m;
int main() {
scanf("%d%d",&n,&m);
for(int i = 1 ; i <= n ; i++)
a[i] = read();
sort(a+1,a+n+1);
for(int i = 1 ; i < n ; i++)
dis[i] = a[i+1]-a[i];
sort(dis+1,dis+n);
long long sum = 0;
for(int i = 1 ; i <= n-m ; i++)
sum+=dis[i];
printf("%lld",sum);
}
问题 C: 上楼梯
题目描述
明明上n 级台阶可用四种步幅, 当然每种步幅花费的体力也不一样, 对应关系如下
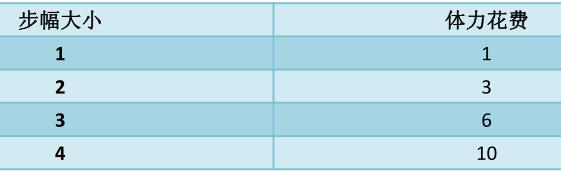
明明开始有m 个体力, 求他最少要跨多少步才能上完所有台阶?
输入
只有n和m两个正整数,中间用空格做间隔符。0<n<=m。
对于30%的数据,m<100
对于60%的数据,m<10000
对于80%的数据,m<1000000
对于100的数据,m<10^19
输出
一个整数,表示最少要跨多少步才能上完所有台阶?
样例输入
3 5
样例输出
2
解题思路
可怕的范围!当数据范围达到10^19时,一定是需要用\(O(1)\)的方法解决问题的。
如果n = 5, m = 5 那么是1 1 1 1 1(每次走一步,总共耗5体力)
如果m成为6,那么就是1 1 1 2
不难发现数对{1, 1} -> {2} 需要多花1点体力
同理 {1, 2} -> {3} 需要多花2点体力 可以推出所有的压缩方式 压缩对象的数值越大 多花费的体力越多
也就是说所需的代价越高,在这个思想下,不难发现,最佳答案是优先将所有1化为2 直到不能化了 再将2化为3
由于需要O(1)的答案,所以直接写数和判断就行了
ll T1= n;
ll T2= (n - (n % 2)) * 3 / 2 + n % 2;
ll T3= (n - (n % 3)) * 2 + n % 3;
ll T4= (n - (n % 4)) * 5 / 2 + n % 4;
T2是尽力将所有走法的全部都变成2所需的体力,最后加上n % 2便是剩下的"1"
T3,T4同理,只不过状态中余的数依然是“1”,所以在代码中需要特判
例如n % 3 = 1 则最后会剩下个1 后面压缩的时候就需要优先压缩{1, 3} -> {4}
然后再压缩{3, 3, 3, 3} -> {4, 4, 4} (也就是lcm的两个因子之间的转移)
#include <iostream>
using namespace std;
#define ll long long
ll n, m;
int main() {
cin>>n>>m;
ll T1= n;
ll temp = m;
ll T2= (n - (n % 2)) * 3 / 2 + n % 2;
ll T3= (n - (n % 3)) * 2 + n % 3;
ll T4= (n - (n % 4)) * 5 / 2 + n % 4;
if(m >= T1 && m < T2) {
temp -= n;
cout<<n - temp<<endl;
} else if(m >= T2 && m < T3) {
temp -= T2;
ll ans = n / 2 + n % 2;
if(n % 2) if(temp >= 2) {
temp -= 2;
ans--;
}
if(temp >= 3) ans -= temp / 3;
cout<<ans<<endl;
} else if(m >= T3 && m < T4) {
temp -= T3;
ll ans = n / 3 + n % 3;
if(n % 3 == 2) {
temp--;
ans--;
}
if(n % 3 == 1 && temp >= 3) {
temp -= 3;
ans--;
}
if(n % 3 == 2 && temp >= 5) {
temp -= 5;
ans--;
}
if(temp >= 6) ans -= temp / 6;
cout<<ans<<endl;
} else {
ll ans = n / 4 + n % 4;
temp -= T4;
if(n % 4 == 2 && temp >= 1) {
temp--;
ans--;
}
if(n % 4 == 3 && temp >= 1) {
temp--;
ans--;
}
if(n % 4 == 3 && temp >= 2) {
temp -= 2;
ans--;
}
cout<<ans<<endl;
}
}
问题 D: 联欢晚会时间
题目描述
A校和B校互为友好学校, 两校教师之间、学生之间常有一些互访交流和联欢活动。今B校的m名学生来到A校, 要与A校的n名学生开一个联欢晚会。会场周围从1 号座位到m+n号座位几乎排了一圈, 只是入口的大门把1 号座位和m+n 号座位隔开了。也就是说, 除了1 号和m+n 号座位外, i(1<i<m+n)号座位与1-i 号和i+1 号座位是相连的。
为增加交流和接触, B 校校方希望本校学生坐的不要过于集中, 为此特作出对B 校学生的限制性规定: 不允许k 名B 校学生座位相连。当然, B 校校方不便要求A 校学生如何坐。
请编程求出满足B 校规定的所有做法共有多少种?
这里所说的坐法对同校学生不加区别。例如当n=3、m=3、k=3 时
BBABAA BBAABA BBAAAB BABBAA
BABABA BABAAB BAABBA BAABAB
BAAABB ABBABA ABBAAB ABABBA
ABABAB ABAABB AABBAB AABABB
符合B校规定的坐法共有这16种。
输入
一行,三个整数,依次为n、m、k, 用空格做间隔符。
对于50%的数据, n、m、k 均不大于10
对于100%的数据, n、m、k 均不大于100
输出
只包含一个整数, 即符合B校规定的坐法总数。
样例输入
3 3 3
样例输出
16
解题思路
需要使用动态规划。
f[i][j][k] : 前i个同学,有j个B校的同学,当前是连续k个B校同学的情况有多少可能性。
f[i][j][0]=sum(f[i-1][j][k]) 其中k=0...K-1当然还要保证k<=j。
f[i][j][k]=f[i-1][j-1][k-1] 只有这一种情况,只需要推k!=0的情况,自然j!=0。
最后求和 sum(f[M+N][M][k])其中k=0...K-1 就是输出的结果。
注意:一定要开long long
#include<cstdio>
long long dp[210][110][110];
int main() {
int n,m,k;
scanf("%d%d%d",&n,&m,&k);
dp[0][0][0] = 1;
for(int i = 1 ; i <= n+m ; i++)
for(int j = 0 ; j <= m ; j++) {
for(int t = 0 ; t <= j && t < k; t++)
dp[i][j][0] += dp[i-1][j][t];
for(int t = 1 ; t <= j && t < k; t++)
dp[i][j][t] = dp[i-1][j-1][t-1];
}
long long ans = 0;
for(int i=0; i<k; i++)
ans+=dp[m+n][m][i];
printf("%lld",ans);
}
问题 E: 梯形面积
题目描述
最近楠楠的数学老师在教他计算梯形面积,由于测验时他不小心计算错了一道求等腰梯形面积的题目,楠楠的老师要罚他计算N道这样的题,这太痛苦了!楠楠求你编个程序来帮助他快速计算面积。
已经知道每道题给如下图形状的等腰梯形中的A,B,C三个参数,请编程计算它的面积。
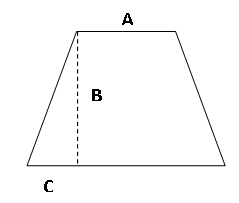
输入
一行3个正整数A,B,C,分别表示等腰梯形的上底宽、高和左边突出的长度(即下底宽为A+2C )。
输出
一行,一个整数,表示梯形的面积。
样例输入
2 3 1
样例输出
9
提示
10个数据:A,B,C的范围是[1…20]。
解题思路
面积等于上底加下底乘宽除二。
#include<cstdio>
int main() {
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
printf("%d",(a+c)*b);
}
问题 F: 网络信号
题目描述
楠楠来到科技馆参加一个网络信息探测试验活动。试验时中间有一个WiFi网络路由器,以路由器为中心半径为R的圆内(包括圆周上)的手机都可以收到网络信号,而圆外的手机就接收不到信号。楠楠拿着手机,一开始在中间,然后每次向左或向右走动一定距离,停下测试一下网络信号。问有多少次测试是可以接收到网络信号的。
例如:R=8米,楠楠一共测试了4次。第一次向左走3米;第二次向左再走4米;第三次向左再走2米;第四次向右再走12米,结果只有第3次测试楠楠是接收不到信号的,其它3次测试都可以接收到网络信号。

输入
第一行,2个正整数R和N。分别表示网络路由器的工作半径和楠楠的测试次数。
第二行,N个整数。第i个整数Di表示楠楠第i次向左或向右移动的距离,如果Di是负整数,则表示楠楠第i次测试是向左移动了|Di|米的距离。如果Di是非负整数,则表示楠楠第i次测试是向右移动了Di米距离。
输出
一个整数。表示楠楠有多少次测试是可以接收到网络信号的。
样例输入
4 5
2 2 2 -8 -8
样例输出
3
提示
第1、2、4次都半径为4的圆内,所以可以接收信号
10个数据:R,N的范围是[1…100]。每次移动距离的范围是[-100…100]。
解题思路
模拟位置即可。使用now表示现在的位置,如果现在的位置在\(|r|\)之内,答案加一,最后输出答案。
#include<cstdio>
int main() {
int r,n;
scanf("%d%d",&r,&n);
int ans = 0,t,now = 0;
for(int i = 1 ; i <= n ; i++) {
scanf("%d",&t);
now+=t;
if(now<=r&&now>=-1*r) ans++;
}
printf("%d",ans);
}
问题 G: 排队I
题目描述
楠楠最近在研究南海区5年级英语成绩的排序有关算法,如果数列中的数是从小到大排列的,则称有序的。研究中对于没有排好序的数列,要统计每个数前面有多少比它大的数字。比如有5个数的数列: 3 1 4 2 5,则第1个数3之前有0个数比它大;第2个数1之前有1个数比它大;第3个数4之前有0个数比它大;第4个数2之前有2个数比它大;第5个数5之前有0个数比它大。由于数列很长,楠楠求你编程来统计。
输入
第一行1个整数N,表示数列有N个整数。
第二行有N个非负整数,每个数表示一个分数,范围是[0…120]。
输出
一行N个非负整数(每个非负整数后面有一个空格),第i个数表示原数列中第i位前有多少比第i位数大。
样例输入
5
3 1 4 2 5
样例输出
0 1 0 2 0
提示
8个的数据: N的范围是[1…1000],每个数范围是[0…120]
2个的数据:N的范围是[1…1,00,000],每个数范围是[0…120]
解题思路
N大小范围在0到120之内,所以我们使用桶排序的思想,\(pail[i]\)表示有多少个i。每读一个数,就去查找i到120有多少个数字。
#include<cstdio>
int pail[200];
int main() {
int n;
scanf("%d",&n);
for(int i = 1 ; i <= n ; i++) {
int t;
scanf("%d",&t);
pail[t]++;
int ans = 0;
for(int j = t+1 ; j <= 120 ; j++)
ans+=pail[j];
printf("%d ",ans);
}
问题 H: 覆盖
题目描述
楠楠的学校有B个男生和G个女生都来到一个巨大的操场上,操场可以看成是N行M列的方格矩阵,如下图(1)是一个4行5列的方格矩阵。每个男生负责打扫一些连续的行,每个女生负责打扫一些连续的列。比如有两个男生,第一个男生负责第1、2两行、第二个男生负责第4行,如图(2)的蓝色。打扫的区域可能重复,比如,又有两个女生,第一个女生负责打扫第3、4两列,第二个女生负责打扫第4、5两列,如图(3)的红色。从图(3)可以容易看出,有颜色覆盖的方格数为18,即这4名学生总共打扫了18个方格。
老师要楠楠在学校给出打扫安排的数据后快速计算出这些学生总共打扫了多少方格?

输入
第一行4个正整数:N,M,B,G,N表示方阵行数,M表示方阵列数,B表示男生数,G表示女生数。
接下来B行,每行两个整数x y。表示相应某个男生负责打扫从第x行到第y行(共y-x+1行),保证1≤x≤y≤N。
再接下来G行,每行两个整数x y。表示相应某个女生负责打扫从第x列到第y列(共y-x+1列),保证1≤x≤y≤M。
输出
一个整数,表示所打扫的面积。
样例输入
4 5 2 2
1 2
4 4
3 4
4 5
样例输出
18
提示
8个的数据:N,M,B,G的范围都是[1…100]
2个的数据:N,M,B,G的范围都是[1…5,000]
解题思路
题目有可能出现重复打扫的情况,为了避免重复计算,我们使用a、b记录每一行列是否被打扫,被打扫了就记作1,这样,输入完成之后计算被打扫的行数、列数,再减去重复部分即可。
#include<cstdio>
int a[5500];//记录第i行是否被打扫
int b[5500];//记录第j列是否被打扫
int main() {
int N,M,B,G;
scanf("%d%d%d%d",&N,&M,&B,&G);
for(int i = 1 ; i <= B ; i++) {
int l,r;
scanf("%d%d",&l,&r);
for(int j = l ; j <= r ; j++)
a[j] = 1;
}
for(int i = 1 ; i <= G ; i++) {
int l,r;
scanf("%d%d",&l,&r);
for(int j = l ; j <= r ; j++)
b[j] = 1;
}
int len = 0;
for(int i = 1 ; i <= 5000;i++)
if(a[i]) len++;
int width = 0;
for(int i = 1 ; i <= 5000;i++)
if(b[i]) width++;
printf("%d",len*M+width*N-len*width);
}
问题 I: 游戏
题目描述
今天是星期天,小楠楠来找你玩“石头、剪刀、布游戏”。你正在学习信息学,所以想了一种需要编程来玩的“石头、剪刀、布游戏”。首先,用数字1,2,3分别表示出石头、剪刀、布。其次,你确定自己前N次“石头、剪刀、布”的出拳方法,下面N次再次同样出拳,…,周而复始;也要求楠楠确定他前M次的出拳方法,然后周而复始。问第K次后,你赢了几次?
例如:N=4,你的前4次出拳方式是“石头、剪刀、布、布”,用数字表示即:”1 2 3 3”。M=5,楠楠前5次出拳方式是“剪刀、石头、石头、布、布” ,用数字表示即:”2 1 1 3 3”。K=10时,情况如下表:

你共赢了5次。
输入
第一行3个整数N,M,K。分别表示你出拳方式的周期长度、楠楠出拳方式的周期长度和总共玩的次数。
第二行有N个整数,每个整数为1、2、3其中之一。
第三行有M个整数,每个整数为1、2、3其中之一。
输出
一个整数,表示K轮出拳后,你赢的次数。
样例输入
5 6 100
1 3 2 2 1
3 3 1 1 1 2
样例输出
29
提示
8个数据: N,M 的范围是[1..100],K的范围是[1…100,000]。
2个数据: N,M的范围是[1..100],K的范围是[1…1,000,000,000]
解题思路
观察到k的范围非常大,暴力算很危险,有概率超时。
由于观察到k内可能存在重复,我们需要算n、m的最小公倍数次数内的赢的次数。删去重复的再对剩余的进行计算即可得到答案。
#include<cstdio>
int gcd(int m, int n) {//辗转相除法求最大公约数
while (n != 0) {
int t = m % n;
m = n;
n = t;
}
return m;
}
int a[3][200];
int main() {
int n,m,k;
scanf("%d%d%d",&n,&m,&k);
for(int i = 1 ; i <= n ; i++)
scanf("%d",&a[0][i]);
for(int i = 1 ; i <= m ; i++)
scanf("%d",&a[1][i]);
int top = m*n/gcd(m,n);//最小公倍数公式
int ans = 0;
for(int i = 1 ; i <= top ; i++) {
int x = (i-1)%n+1,y = (i-1)%m+1;
if(a[0][x]-a[1][y]==-1||a[0][x]-a[1][y]==2)
ans++;
}
ans = k/top*ans;
k%=top;
//对于非重复的,再算一次。
for(int i = 1 ; i <= k ; i++) {
int x = (i-1)%n+1,y = (i-1)%m+1;
if(a[0][x]-a[1][y]==-1||a[0][x]-a[1][y]==2)
ans++;
}
printf("%d",ans);
}
问题 J: 差
题目描述
楠楠在网上刷题,感觉第一题:求两数的和(A+B Problem)太无聊了,于是增加了一题:A-B Problem,难倒了一群小朋友,哈哈。
题目是这样的:给出N个从小到大排好序的整数,一个差值C,要求在这N个整数中找两个数A和B,使得A-B=C,问这样的方案有多少种?
例如:N=5,C=2,5个整数是:2 2 4 8 10。答案是3。具体方案:第3个数减第1个数;第3个数减第2个数;第5个数减第4个数。
输入
第一行2个正整数:N,C。
第二行N个整数:已经有序。注意:可能有相同的。
输出
一个整数,表示该串数中包含的所有满足A-B=C的数对的方案数。
样例输入
4 1
1 1 2 2
样例输出
4
提示
5个数据:N的范围是[1…1,000]。
5个数据:N的范围是[1…100,000]。
所有数据:
C的范围是[1…1,000,000,000]。
N个整数中每个数的范围是:[0…1,000,000,000]。
解题思路
由于已经排序好,我们使用stl库提供的二分查找法:upper_bound、lower_bound计算。在这里,我介绍一下这两个函数。在之后很多题目里面,二分查找是很常用的优化方式,希望同学们掌握。
lower_bound与upper_bound
1.作用
这两个是STL中的函数,作用很相似:
假设我们查找x,那么:
lower_bound会找出序列中第一个大于等于x的数
upper_bound会找出序列中第一个大于x的数
差个等于号╮(╯▽╰)╭
2.用法
以下都以lower_bound做栗子
它们俩使用的前提是一样的:序列是有序的
对于一个数组a,在[1,n]的区间内查找大于等于x的数(假设那个数是y),函数就写成:
lower_bound(a + 1, a + 1 + n, x);
函数返回一个指向y的指针
看着是不是很熟悉?回想sort使用的时候:
sort(a, a + 1 + n, cmp);
这里a+1,a+1+n的写法是不是很像?
同样的,lower_bound和upper_bound也是可以加比较函数cmp的:
lower_bound(a + 1, a + 1 + n, x, cmp);
到这里不得不说说前面的"有序序列",这里的"有序"是对什么有序?
你可能已经猜到了,它是对于比较器有序,并且必须是升序!
一旦对降序序列使用lower_bound,就会出现神奇的错误(看这里)
3. 返回值
返回的是个指针
对于返回值我们有两种处理方式:
第一种:
许多人讨厌指针,那么我们用这个指针减去数组开头的指针(即数组名),得到两个指针的差,就是数组下标,即:
int p = lower_bound(懒得写) - a;
那么a[p]就是要找的y
(如果不知道为什么就记着好了)
第二种:
int *p = lower_bound(还是懒得写);
那么*p就是要找的y
如果需要查升序序列里一个数的数量,用upper_bound-lower_bound即可。
#include<iostream>
#include<algorithm>
using namespace std;
int a[110000];
int main() {
int n,c,ans=0;
cin >> n >> c;
for(int i = 1 ; i <= n ; i++) {
cin >> a[i];
int findNum = a[i]-c;
if(lower_bound(a+1,a+i,findNum))
ans += upper_bound(a+1,a+i,findNum) - lower_bound(a+1,a+i,findNum);
}
cout << ans;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号