剑指offer-下
丑数
把只包含质因子2、3和5的数称作丑数(Ugly Number)。例如6、8都是丑数,但14不是,因为它包含质因子7。 习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。
public int GetUglyNumber_Solution(int index) {
if(index==0)return 0;
ArrayList<Integer> list=new ArrayList<Integer>();
list.add(1);
int i2=0,i3=0,i5=0;//存放三个队列的头位置
while(list.size()<index)//循环的条件
{
int m2=list.get(i2)*2;
int m3=list.get(i3)*3;
int m5=list.get(i5)*5;
int min=Math.min(m2,Math.min(m3,m5));
list.add(min);
if(min==m2)i2++;
if(min==m3)i3++;
if(min==m5)i5++;
}
return list.get(list.size()-1);
}
第一个只出现一次的字符
public int FirstNotRepeatingChar(String str) {
int count=-1;
int index=0;
int[] chars = new int[128];
for(int i=0;i<str.length();i++){
index=(int)str.charAt(i);
if(chars[index]==0){
chars[index]=count;
count--;
}
else {chars[index]=1;count--;}
}
int max=-10001;
int min_index=0;
for(int i=0;i<128;i++){
if(chars[i]<0 && chars[i]>max){
max=chars[i];
min_index = i;
}
}
if(max==-10001) return -1;
return max*-1-1;
}
// 思路是初始的int[] 记录出现的位置(负值),再次出现后转为正值。之后就是找负值最大的就是最先出现的
数组中的逆序对
input: 1,2,3,4,5,6,7,0
output: 7
归并排序的改进,把数据分成前后两个数组(递归分到每个数组仅有一个数据项),合并数组,
合并时,出现前面的数组值array[i]大于后面数组值array[j]时;则前面数组array[i]~array[mid]都是大于array[j]的,count += mid+1 - i参考剑指Offer,但是感觉剑指Offer归并过程少了一步拷贝过程。还有就是测试用例输出结果比较大,对每次返回的count mod(1000000007)求余
public class Solution {
public int InversePairs(int [] array) {
if(array==null || array.length<=1) return 0;
int[] copy = new int[array.length];
System.arraycopy(array, 0, copy, 0, array.length);
return mergeSort(array, copy, 0, array.length-1);
}
private int mergeSort(int [] array, int [] copy, int start, int end){
if(start>=end) return 0;
int mid = (end+start)>>1;//等价于/2
int left = mergeSort(array, copy, start, mid);
int right = mergeSort(array, copy, mid+1, end);
int foreidx = mid; //前半部分指标
int backidx = end; //后半部分指标
int counts = 0; //记录本次逆序对数量
int idxcopy = end; //辅助数组的下标
while(foreidx>=start && backidx >= mid+1){
if(array[foreidx] > array[backidx]){
copy[idxcopy--] = array[foreidx--];
counts += backidx - mid;
if(counts>1000000007) counts %= 1000000007;
}
else copy[idxcopy--] = array[backidx--];
}
while(foreidx>=start){
copy[idxcopy--] = array[foreidx--];
}
while(backidx>mid){
copy[idxcopy--] = array[backidx--];
}
for(int i=start;i<=end;i++){
array[i] = copy[i];
}
return (left+right+counts)% 1000000007;
}
}
两个链表第一个公共结点
public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
ListNode p1=pHead1,p2=pHead2;
while(p1!=p2){
p1 = p1==null?pHead2:p1.next;
p2 = p2==null?pHead1:p2.next;
}
return p1;
}
统计数字出现次数
public int GetNumberOfK(int [] array , int k) {
int count=0;
char kk = (char)(k+'0');
StringBuilder sb = new StringBuilder();
for(int i=0;i<array.length;i++){
sb.append(array[i]+"");
}
for(int i=0;i<sb.length();i++){
if(sb.charAt(i)==kk) count++;
}
return count;
}
二叉树的深度
非递归解法,层次遍历求深度
/**
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
import java.util.Queue;
import java.util.LinkedList;
public class Solution {
public int TreeDepth(TreeNode pRoot) {
if(pRoot == null) return 0;
Queue<TreeNode> queue = new LinkedList<TreeNode>();
queue.add(pRoot);
int depth = 0, count = 0, nextCount = 1;
while(queue.size()!=0){
TreeNode top = queue.poll();
count++;
if(top.left != null) queue.add(top.left);
if(top.right != null) queue.add(top.right);
if(count == nextCount){
nextCount = queue.size();
count = 0;
depth++;
}
}
return depth;
}
}
递归解法
import java.lang.Math;
public class Solution {
public int TreeDepth(TreeNode pRoot) {
if(pRoot == null) return 0;
int left = TreeDepth(pRoot.left);
int right = TreeDepth(pRoot.right);
return Math.max(left, right) + 1;
}
}
数组中只出现一次的两个数
位运算中异或的性质:两个相同数字异或=0,一个数和0异或还是它本身。
将所有所有数字相异或,则最后的结果肯定是那两个只出现一次的数字异或的结果
依照这个思路,我们来看两个数(我们假设是AB)出现一次的数组。我们首先还是先异或,
剩下的数字肯定是A、B异或的结果,这个结果的二进制中的1,表现的是A和B的不同的位。
我们就取第一个1所在的位数,假设是第3位,接着把原数组分成两组,分组标准是第3位是否为1。
如此,相同的数肯定在一个组,因为相同数字所有位都相同,而不同的数,肯定不在一组。
然后把这两个组分别逐位异或,剩余的两个结果就是这两个只出现一次的数字。
//num1,num2分别为长度为1的数组。传出参数
//将num1[0],num2[0]设置为返回结果
public class Solution {
//位运算中异或的性质:两个相同数字异或=0,一个数和0异或还是它本身。
//将所有所有数字相异或,则最后的结果肯定是那两个只出现一次的数字异或的结果
/*依照这个思路,我们来看两个数(我们假设是AB)出现一次的数组。我们首先还是先异或,
剩下的数字肯定是A、B异或的结果,这个结果的二进制中的1,表现的是A和B的不同的位。
我们就取第一个1所在的位数,假设是第3位,接着把原数组分成两组,分组标准是第3位是否为1。
如此,相同的数肯定在一个组,因为相同数字所有位都相同,而不同的数,肯定不在一组。
然后把这两个组分别逐位异或,剩余的两个结果就是这两个只出现一次的数字。
*/
public void FindNumsAppearOnce(int [] array,int num1[] , int num2[]) {
if(array.length<2) return ;
int n = array.length;
int temp = array[0];
for(int i=1;i<n;i++){
temp = temp^array[i];
}
if(temp==0) return ;
int index=0;
while((temp&1)==0){
temp=temp>>1;
++index;
}
num1[0] = 0;
num2[0] = 0;
for(int i=0;i<n;i++){
if(IsBit(array[i],index)) num1[0]^=array[i];
else num2[0]^=array[i];
}
}
private boolean IsBit(int num, int index){
num = num>>index;
return ( (num&1)==1 );
}
}
和为S的正数序列
双指针技术,就是相当于有一个窗口,窗口的左右两边就是两个指针,我们根据窗口内值之和来确定窗口的位置和宽度。非常牛逼的思路,虽然双指针或者所谓的滑动窗口技巧还是蛮常见的
public ArrayList<ArrayList<Integer> > FindContinuousSequence(int sum) {
//存放结果
ArrayList<ArrayList<Integer> > result = new ArrayList<>();
//两个起点,相当于动态窗口的两边,根据其窗口内的值的和来确定窗口的位置和大小
int plow = 1,phigh = 2;
while(phigh > plow){
//由于是连续的,差为1的一个序列,那么求和公式是(a0+an)*n/2
int cur = (phigh + plow) * (phigh - plow + 1) / 2;
//相等,那么就将窗口范围的所有数添加进结果集
if(cur == sum){
ArrayList<Integer> list = new ArrayList<>();
for(int i=plow;i<=phigh;i++) list.add(i);
result.add(list);
plow++;
//如果当前窗口内的值之和小于sum,那么右边窗口右移一下
}else if(cur < sum) phigh++;
else{
//如果当前窗口内的值之和大于sum,那么左边窗口右移一下
plow++;
}
}
return result;
}
和为S的两个数字
输入一个递增排序的数组和一个数字S,在数组中查找两个数,使得他们的和正好是S,如果有多对数字的和等于S,输出两个数的乘积最小的。
和相同的情况下,外围的两个数的乘积最小,采用双指针夹逼法
public ArrayList<Integer> FindNumbersWithSum(int [] array,int sum) {
//和相同的情况下,外围的两个数的乘积最小,采用双指针夹逼法
ArrayList<Integer> list = new ArrayList<>();
if (array == null || array.length == 0)
return list;
int left = 0;
int right = array.length - 1; //和上一道题有所不同,结尾的位置在最后。但是在2也是可以的
while (left < right) {
int total = array[left] + array[right];
if (total == sum) {
list.add(array[left]);
list.add(array[right]);
return list;
} else if (total > sum) {
//大于sum,说明太大了,right左移寻找更小的数
--right;
} else {
//2.如果和小于sum,说明太小了,left右移寻找更大的数
++left;
}
}
return list;
}
左旋转字符串
对于一个给定的字符序列S,请你把其循环左移K位后的序列输出。例如,字符序列S=”abcXYZdef”,要求输出循环左移3位后的结果,即“XYZdefabc”。
方法:两次旋转法
//两次旋转法
public String LeftRotateString(String str, int n) {
char[] chars = str.toCharArray();
if(chars.length < n) return "";
reverse(chars, 0, n - 1);
reverse(chars, n, chars.length - 1);
reverse(chars, 0, chars.length - 1);
return new String(chars);
}
public void reverse(char[] chars, int start, int end) {
while (start < end) {
char temp = chars[start];
chars[start] = chars[end];
chars[end] = temp;
start++;
end--;
}
}
反转单词序列
“student. a am I”。----------》I am a student.”
public String ReverseSentence(String str) {
if(str.trim().equals("")){
return str;
}
String[] a = str.split(" ");
StringBuffer o = new StringBuffer();
int i;
for (i = a.length; i >0;i--){
o.append(a[i-1]);
if(i > 1){
o.append(" ");
}
}
return o.toString();
}
环的入口结点
public ListNode EntryNodeOfLoop(ListNode pHead)
{
if(pHead==null|| pHead.next==null|| pHead.next.next==null)return null;
ListNode fast=pHead.next.next;
ListNode slow=pHead.next;
/////先判断有没有环
while(fast!=slow){
if(fast.next!=null&& fast.next.next!=null){
fast=fast.next.next;
slow=slow.next; }
else{ //没有环,返回
return null; }
}
//循环出来的话就是有环,且此时fast==slow.
fast=pHead;
while(fast!=slow){
fast=fast.next;
slow=slow.next; }
return slow;
}
删除重复节点
public ListNode deleteDuplication(ListNode pHead)
{
if(pHead==null || pHead.next==null) return pHead;
ListNode current = null;
if(pHead.val==pHead.next.val){
current = pHead.next.next;
while(current!=null && current.val==pHead.val){// 注意判断条件的先后次序
current = current.next;
}
return deleteDuplication(current);
}
else {
current = pHead.next;
pHead.next = deleteDuplication(current);
return pHead;
}
中序遍历下一个结点
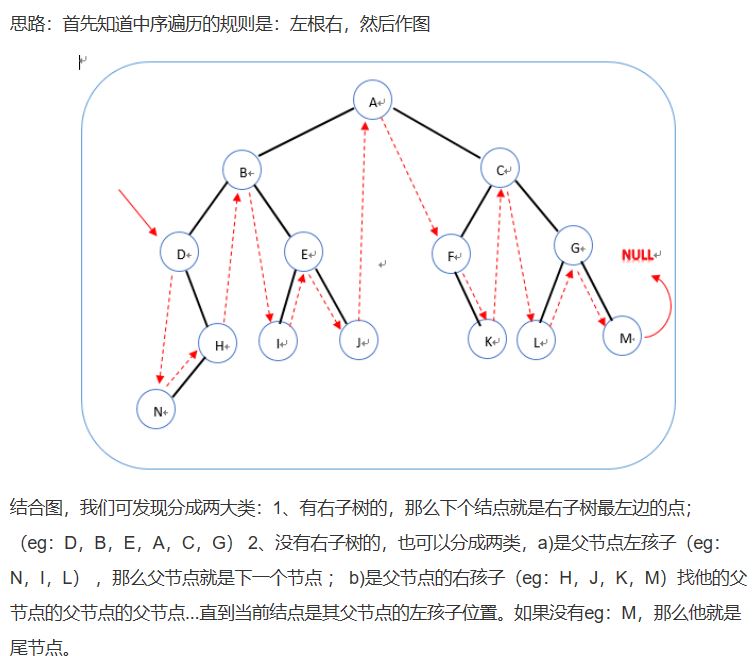
public TreeLinkNode GetNext(TreeLinkNode pNode)
{
if(pNode==null) return null;
if(pNode.right!=null){
pNode = pNode.right;
while(pNode.left!=null)
pNode = pNode.left;
return pNode;
}
while(pNode.next!=null){
TreeLinkNode proot = null;
while(pNode.next!=null){
proot = pNode.next;
if(pNode==proot.left)
return proot;
pNode = pNode.next;
}
}
return null;
}
判断镜像二叉树
boolean isSymmetrical(TreeNode pRoot)
{
if(pRoot == null) return true;
Stack<TreeNode> s = new Stack<>();
s.push(pRoot.left);
s.push(pRoot.right);
while(!s.empty()) {
TreeNode right = s.pop();//成对取出
TreeNode left = s.pop();
if(left == null && right == null) continue;
if(left == null || right == null) return false;
if(left.val != right.val) return false;
//成对插入
s.push(left.left);
s.push(right.right);
s.push(left.right);
s.push(right.left); }
return true;
}
之字形打印二叉树
public ArrayList<ArrayList<Integer>> Print(TreeNode pRoot) {
ArrayList<ArrayList<Integer>> res = new ArrayList<>();
LinkedList<TreeNode> list = new LinkedList<>();// 存储节点,每次一层
if(pRoot != null) list.add(pRoot); boolean flag = true;// true 从左到右
while (!list.isEmpty()) {
int size = list.size();
ArrayList<Integer> layer = new ArrayList<>();
if (flag)
for (int i = 0; i < size; i++) layer.add(list.get(i).val);
else
for (int i = size - 1; i >= 0; i--) layer.add(list.get(i).val);
flag = !flag;
res.add(layer);
for (int i = 0; i < size; i++) {
TreeNode node = list.poll();
if (node.left != null) list.add(node.left);
if (node.right != null) list.add(node.right);
}
}
return res;
}
逐层打印二叉树
ArrayList<ArrayList<Integer> > Print(TreeNode pRoot) {
ArrayList<ArrayList<Integer>> res = new ArrayList<>();
LinkedList<TreeNode> list = new LinkedList<>();// 存储节点,每次一层
if(pRoot != null) list.add(pRoot);
while (!list.isEmpty()) {
int size = list.size();
ArrayList<Integer> layer = new ArrayList<>();
for (int i = 0; i < size; i++) layer.add(list.get(i).val);
res.add(layer);
for (int i = 0; i < size; i++) {
TreeNode node = list.poll();
if (node.left != null) list.add(node.left);
if (node.right != null) list.add(node.right);
}
}
return res;
}
二叉搜索树第k个结点
//思路:二叉搜索树按照中序遍历的顺序打印出来正好就是排序好的顺序。
// 所以,按照中序遍历顺序找到第k个结点就是结果。
public class Solution {
int index = 0; //计数器
TreeNode KthNode(TreeNode root, int k) {
if(root != null){ //中序遍历寻找第k个
TreeNode node = KthNode(root.left,k);
if(node != null)
return node;
index ++;
if(index == k)
return root;
node = KthNode(root.right,k);
if(node != null)
return node;
}
return null;
}
}
数组中重复的数字
public boolean duplicate(int numbers[],int length,int [] duplication) {
boolean [] k = new boolean[length];
for(int i=0;i<length;i++){
if(k[numbers[i]]==true) {
duplication[0]=numbers[i];
return true;}
else k[numbers[i]]=true;
}
return false;
}
剪绳子
/** * 题目分析: * 先举几个例子,可以看出规律来。
4 : 2*2 *
5 : 2*3 *
6 : 3*3 *
7 : 2*2*3 或者4*3 *
8 : 2*3*3 *
9 : 3*3*3 *
10:2*2*3*3 或者4*3*3 *
11:2*3*3*3 *
12:3*3*3*3 *
13:2*2*3*3*3 或者4*3*3*3 * * 下面是分析:
首先判断k[0]到k[m]可能有哪些数字,实际上只可能是2或者3。
* 当然也可能有4,但是4=2*2,我们就简单些不考虑了。
* 5<2*3,6<3*3,比6更大的数字我们就更不用考虑了,肯定要继续分。
* 其次看2和3的数量,2的数量肯定小于3个,为什么呢?因为2*2*2<3*3,那么题目就简单了。
* 直接用n除以3,根据得到的余数判断是一个2还是两个2还是没有2就行了。
* 由于题目规定m>1,所以2只能是1*1,3只能是2*1,这两个特殊情况直接返回就行了。 *
* 乘方运算的复杂度为:O(log n),用动态规划来做会耗时比较多。 */
public int cutRope(int target) {
if(target<2) return target;
if(target==2) return 1;
if(target==3) return 2;
if(target==4) return 4;
int three = (int)(target/3);
int two = (int)((target-three*3)/2);
int result = (int)(Math.pow(3,three)) * (int)(Math.pow(2,two));
return result;
}
机器人的运动范围
public int movingCount(int threshold, int rows, int cols)
{
boolean [][] visited = new boolean[rows][cols];
return countingSteps(threshold,rows,cols,0,0,visited);
}
private int countingSteps(int limit,int rows,int cols,int r,int c,boolean[][] visited){
if (r < 0 || r >= rows || c < 0 || c >= cols|| visited[r][c] || bitSum(r) + bitSum(c) > limit)
return 0;
visited[r][c] = true;
return countingSteps(limit,rows,cols,r - 1,c,visited)
+ countingSteps(limit,rows,cols,r,c - 1,visited)
+ countingSteps(limit,rows,cols,r + 1,c,visited)
+ countingSteps(limit,rows,cols,r,c + 1,visited)
+ 1;
}
private int bitSum(int t){
int count = 0;
while (t != 0){
count += t % 10;
t /= 10;
}
return count;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号