竞赛191
切割后面积最大的蛋糕
矩形蛋糕的高度为 h 且宽度为 w,给你两个整数数组 horizontalCuts 和 verticalCuts,其中 horizontalCuts[i] 是从矩形蛋糕顶部到第 i 个水平切口的距离,类似地, verticalCuts[j] 是从矩形蛋糕的左侧到第 j 个竖直切口的距离。
请你按数组 horizontalCuts 和 verticalCuts 中提供的水平和竖直位置切割后,请你找出 面积最大 的那份蛋糕,并返回其 面积 。由于答案可能是一个很大的数字,因此需要将结果对 10^9 + 7 取余后返回。
示例 1:
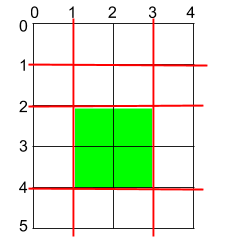
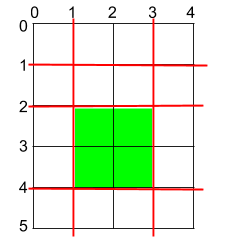
输入:h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3] 输出:4 解释:上图所示的矩阵蛋糕中,红色线表示水平和竖直方向上的切口。切割蛋糕后,绿色的那份蛋糕面积最大。
示例 2:
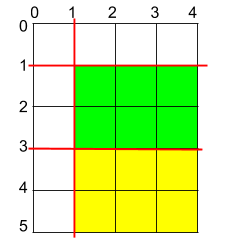
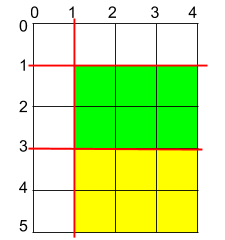
输入:h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1] 输出:6 解释:上图所示的矩阵蛋糕中,红色线表示水平和竖直方向上的切口。切割蛋糕后,绿色和黄色的两份蛋糕面积最大。
示例 3:
输入:h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3] 输出:9
提示:
2 <= h, w <= 10^91 <= horizontalCuts.length < min(h, 10^5)1 <= verticalCuts.length < min(w, 10^5)1 <= horizontalCuts[i] < h1 <= verticalCuts[i] < w- 题目数据保证
horizontalCuts中的所有元素各不相同 - 题目数据保证
verticalCuts中的所有元素各不相同
/**
* @param {number} h
* @param {number} w
* @param {number[]} horizontalCuts
* @param {number[]} verticalCuts
* @return {number}
*/
var maxArea = function(h, w, horizontalCuts, verticalCuts) {
horizontalCuts.sort((a, b)=>a-b);
horizontalCuts.unshift(0);
horizontalCuts.push(h);
verticalCuts.sort((a, b)=>a-b);
verticalCuts.unshift(0);
verticalCuts.push(w);
let mod = 10**9 + 7;
let hlen = horizontalCuts.length;
let vlen = verticalCuts.length;
let r = -Infinity;
let mh = -Infinity;
let mv = -Infinity
for(let i=1; i<hlen; i++){
let l2 = (horizontalCuts[i]-horizontalCuts[i-1])%mod;
if(l2>=mh){
mh = l2
}
}
for(let j=1; j<vlen; j++){
let l1 = (verticalCuts[j]-verticalCuts[j-1])%mod;
if(l1>=mv){
mv = l1
}
}
console.log(mv, mv)
return mh*mv%mod
// return r;
};
当时就差1分钟,甚至都不到一分钟提交通过,之前双层for循环超时间限制,后来改成上面那样,但是最后测试用例求出的值太大。脑子里有个固定思维 “中等*中等 > 最大乘*某值”,一直没发现是最终结果没取模mod, mh*mv%mod,这就是固定思维的弊端!!!!,可能就是某件事做多了,自然想到某个点,可能正确,可能不正确,本质上还是没彻底想明白这个题意。这个题里面切割蛋糕,中等值能取到最大值进行相乘,为什么不最大*最大呢。最后想到结果也要取模,结果写了2个mv,后来一看才发现应该是mv*mh。话说今天并发量太高,迟到5分钟才打开网站。
两个盒子中球的颜色数相同的概率
桌面上有 2n 个颜色不完全相同的球,球上的颜色共有 k 种。给你一个大小为 k 的整数数组 balls ,其中 balls[i] 是颜色为 i 的球的数量。
所有的球都已经 随机打乱顺序 ,前 n 个球放入第一个盒子,后 n 个球放入另一个盒子(请认真阅读示例 2 的解释部分)。
注意:这两个盒子是不同的。例如,两个球颜色分别为 a 和 b,盒子分别为 [] 和 (),那么 [a] (b) 和 [b] (a) 这两种分配方式是不同的(请认真阅读示例 1 的解释部分)。
示例 1:
输入:balls = [1,1] 输出:1.00000 解释:球平均分配的方式只有两种: - 颜色为 1 的球放入第一个盒子,颜色为 2 的球放入第二个盒子 - 颜色为 2 的球放入第一个盒子,颜色为 1 的球放入第二个盒子 这两种分配,两个盒子中球的颜色数都相同。所以概率为 2/2 = 1 。
示例 2:
输入:balls = [2,1,1] 输出:0.66667 解释:球的列表为 [1, 1, 2, 3] 随机打乱,得到 12 种等概率的不同打乱方案,每种方案概率为 1/12 : [1,1 / 2,3], [1,1 / 3,2], [1,2 / 1,3], [1,2 / 3,1], [1,3 / 1,2], [1,3 / 2,1], [2,1 / 1,3], [2,1 / 3,1], [2,3 / 1,1], [3,1 / 1,2], [3,1 / 2,1], [3,2 / 1,1] 然后,我们将前两个球放入第一个盒子,后两个球放入第二个盒子。 这 12 种可能的随机打乱方式中的 8 种满足「两个盒子中球的颜色数相同」。 概率 = 8/12 = 0.66667
示例 3:
输入:balls = [1,2,1,2] 输出:0.60000 解释:球的列表为 [1, 2, 2, 3, 4, 4]。要想显示所有 180 种随机打乱方案是很难的,但只检查「两个盒子中球的颜色数相同」的 108 种情况是比较容易的。 概率 = 108 / 180 = 0.6 。
示例 4:
输入:balls = [3,2,1] 输出:0.30000 解释:球的列表为 [1, 1, 1, 2, 2, 3]。要想显示所有 60 种随机打乱方案是很难的,但只检查「两个盒子中球的颜色数相同」的 18 种情况是比较容易的。 概率 = 18 / 60 = 0.3 。
示例 5:
输入:balls = [6,6,6,6,6,6] 输出:0.90327
提示:
1 <= balls.length <= 81 <= balls[i] <= 6sum(balls)是偶数- 答案与真实值误差在
10^-5以内,则被视为正确答案
请计算「两个盒子中球的颜色数相同」的情况的概率。
/// 这个会超出时间限制
var getProbability = function(balls) {
const dp = [];
for(let t1 = 0; t1<50; t1++){
dp[t1] = [];
for(let t2 = 0; t2<50; t2++){
dp[t1][t2] = [];
for(let t3 = 0; t3<9; t3++){
dp[t1][t2][t3] = [];
for(let t4 = 0; t4<9; t4++){
dp[t1][t2][t3][t4] = [];
for(let t5 = 0; t5<9; t5++){
dp[t1][t2][t3][t4][t5] = [];
for(let t6 = 0; t6<9; t6++){
dp[t1][t2][t3][t4][t5][t6] = 0;
}
}
}
}
}
}
let c = [];
let n = balls.length;
let tot = 0;
for(let i=0;i<n;i++){
for(let j=0;j<balls[i];j++)
c.push(i+1);
}
let N = c.length;
dp[0][0][0][0][0][0] = 1;
for(let i=0;i<N;i++){
for(let n1=0;n1<=N/2;n1++){
for(let lc1=0;lc1<=n;lc1++){
for(let lc2=0;lc2<=n;lc2++){
for(let c1=0;c1<=n;c1++){
for(let c2=0;c2<=n;c2++){
if(dp[i][n1][lc1][lc2][c1][c2]==0)continue;
let p1 = (N/2-n1)*1.0/(N-i);
let p2 = 1-p1;
if(c[i]!=lc1){
dp[i+1][n1+1][c[i]][lc2][c1+1][c2] += dp[i][n1][lc1][lc2][c1][c2]*p1;
}
else{
dp[i+1][n1+1][lc1][lc2][c1][c2] += dp[i][n1][lc1][lc2][c1][c2]*p1;
}
if(c[i]!=lc2){
dp[i+1][n1][lc1][c[i]][c1][c2+1] += dp[i][n1][lc1][lc2][c1][c2]*p2;
}
else{
dp[i+1][n1][lc1][lc2][c1][c2] += dp[i][n1][lc1][lc2][c1][c2]*p2;
}
}
}
}
}
}
}
let ans = 0;
for(let lc1=0;lc1<=n;lc1++)
for(let lc2=0;lc2<=n;lc2++)
for(let c1=0;c1<=n;c1++){
ans += dp[N][N/2][lc1][lc2][c1][c1];
}
return ans;
};


 浙公网安备 33010602011771号
浙公网安备 33010602011771号