线性代数新感悟（一）

一 线性代数

1.1       方程组的几何解释

例如：2 × 2方程组：2x – y = 0 和 -x + 2y = 3

从横向看：代表在平面xy坐标系中两条直线的交点情况。

从纵向看：x(2，-1)^T + y(-1，2)^T = (0，3)^T ，x和y为两个向量的未知系数，可以看作是等号左边两个向量进行线性组合得到等号右边向量。只有右边的向量落在左边向量组成的空间之内，方程组才有解。

方程组，一方面对应空间几何意义，一方面又有向量的线性组合关系，此之谓线性代数。

1.2       对于方程组Ax = b 以及矩阵AB = C的理解

 

 

 

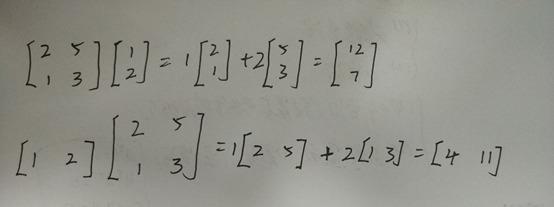
如上图所示，对一个矩阵A右乘一个列向量，相当于对矩阵A的列向量进行线性组合求得一个列向量。对矩阵A左乘一个行向量，相当于对矩阵A的行向量进行线性组合求得一个行向量。

由上述结论推理，若是对矩阵A右乘（左乘）多个列（行）向量，得到的多个列（行）向量又可以组成一个矩阵，这就是矩阵的乘法AB = C，例如：

 

 

 

当然，除此之外，矩阵的乘法运算有其计算公式。并且多个矩阵的乘法运算例如：(AB)C = A(BC)，括号的位置可以改变，但是矩阵之间相对的前后顺序是不可以改变的。

1.3       向量空间

n维向量空间Rⁿ，必须包含零向零即原点，并且在空间内可以做各种向量运算，如数乘，线性组合等等。

Rⁿ最大的子空间是其本身，最小的子空间为零向量即原点。在最大和最小之间的子空间是过原点的维数逐渐加大的各空间。

Ax = 0以及Ax = b的解集分别为A的零（子）空间和列向量（子）空间。线性代数中4个基本的子空间为：1. 列向量空间，2. 零空间， 3. 行空间（其解法可以通过将矩阵A进行转置之后进行列处理得到）， 4. A转之后的零空间（左0空间）

1.4  A_m×nx = b的解的数量

a)        r(A) < r(A, b)时，无解

b)        r(A) = r(A, b)时，有解

c)        r(A) = r(A, b) = n时，有唯一解；r(A) = r(A, b) < n时，有无穷解。

d)        对于矩阵A，若n > m ，要么无穷解，要么无解。若n < m，没啥特殊的，按上述abc分析就可。