Dijkstra算法

什么是？解决什么问题？缺点？

问题描述：在无向有权图G = （V，E）中，假设每条边E[i]的长度是w[i],找到由顶点V0到其余各点的最短路径。

Dijkstra算法是典型的单源最短路径算法，用于计算一个节点到其他节点的最短距离。主要特点是以起始点为中心向外层扩展，直到扩展到终点为止，与BFS有几分相似。Dijkstra存在局限性，即不能处理负权边。

算法描述

设G = (V,E)是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径，就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第二组为其余未确定最短路径的顶点的集合（用U表示），按最短路径长度的递增次序以此把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中个顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。

算法步骤

1、详细

• 初始时，S只包括起点v；U包含除v外的其他顶点，且U[i]表示顶点i到起点的距离。
• 从U中选出“距离起点最短的顶点a”，并将顶点k加入到S中，同时，从U中移除顶点a；
• 从顶点a出发，更新U中各个顶点到起点v的距离，dis[b] = min(dis[b], dis[a] + ab);

2、简略

• 找到当前没有访问的最短路节点；（找最小值）
• 确认这个节点的最短路就是当前大小；（确定一个解）
• 根据这个节点的最短路大小，更新其他节点的路径长度。（根据确定的解更新）

3、图片说明

 

 

 

 

 

 

 

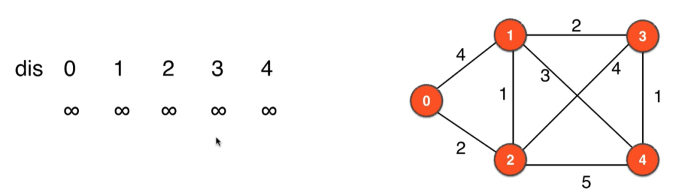
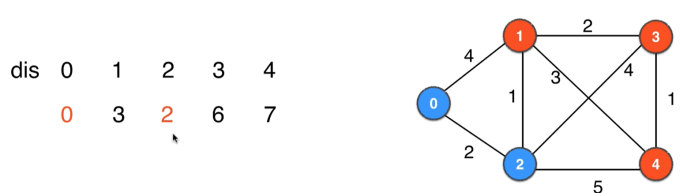
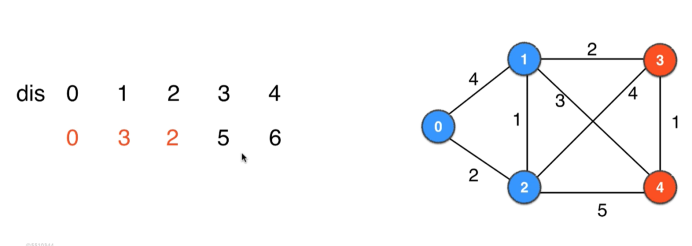
 代码（优化后的方法，与步骤不一致，所述步骤时间复杂度是O(V^2),代码的时间复杂度为O（V），差别在于使用了优先队列）

 

#include <iostream>
#include <fstream>
#include <vector>
#include <queue>
#include <bitset>

#define FIN "dijkstra.in"
#define FOUT "dijkstra.out"
#define oo ((1LL<<31) - 1)
#define MAXN 50005

using namespace std;

int nodes, edges;

vector<pair<int, int>> Graph[MAXN];
int distMin[MAXN];
struct Node{
    int point;
    int value;
    Node(int a, int b){
        point = a;
        value = b;
    }

    bool operator<(const Node &a) const{
        if(value == a.value){
            return point < a.point;
        }
        return value > a.value;
    }
};

priority_queue<Node> Queue;
bitset<MAXN> inQueue;

void readData() {
    int x, y, cost;
    ifstream fin(FIN);
    fin >> nodes >> edges;

    while (edges--) {
        fin >> x >> y >> cost;
        Graph[x].push_back({y, cost});
        Graph[y].push_back({x, cost});
    }
    fin.close();
}

void Dijkstra() {
    for (int i = 2; i <= nodes; i++)
        distMin[i] = oo;
    distMin[1] = 0;
    Queue.push(Node(1, 0));
    inQueue[1] = true;

    while (!Queue.empty()) {
        Node node = Queue.top();
        Queue.pop();
　　　　 if(inQueue[node.point]) continue;
        inQueue[node.point] = true;
        for (auto it : Graph[node.point]) {
            if(!inQueue[it.first]){
                if(distMin[it.first] > distMin[node.point] + it.second){
                    distMin[it.first] = distMin[node.point] + it.second;
                    Queue.push(Node(it.first, distMin[it.first]));
                }
            }
        }
    }
}

void writeData() {
    ofstream fout(FOUT);
    for (int i = 2; i <= nodes; ++i)
        (distMin[i] < oo) ? fout << i << ": " << distMin[i] << endl : fout << i <<": " << 0 << endl;
    fout.close();
}

int main() {
    readData();
    Dijkstra();
    writeData();
    return 0;
}

 

输入文件dijkstra.in

5 9
1 2 1
1 3 9
1 5 3
2 4 3
2 3 7
4 3 2
4 1 1
5 2 4
5 4 2

输出文件结果如下：

2: 1
3: 3
4: 1
5: 3