CF321E Ciel and Gondolas || 决策单调性 wqs二分优化DP 学习笔记

因为其他题解写的都十分模糊，所以打算自己整理一下

题目链接：
luogu
codeforces

分析题目

考虑定义二维$DP$ :$dp[i][j]$表示对于前$i$个人进入$j$个座舱其最小的总陌生值

显然可以推出转移方程：$dp[i][j]=min(dp[k][j-1]+(sum[i][i]+sum[k][k]-sum[i][k]-sum[k][i])/2)$

发现时间复杂度是$O(n^2 k)$，显然会TLE，所以要进行优化。

RT：本题使用了 决策单调性 和 wqs二分优化DP
所以要学前置知识

前置知识

决策单调性优化DP（四边形不等式优化DP）

字面意思，即用四边形不等式来判定决策单调性，通过维护决策单调性来优化DP
通常DP转移方程为

\[dp_i=min_{j=1}^i dp_j+w(j,i) \]

其中$w(j,i)$为区间$[j,i]$的权值，且恒定不变。

概念以及相关证明

决策单调性的概念
假如对于某一个dp方程，$dp(i)$的最优转移是$dp(k_i)$，那么称$k_i$为$i$的决策点。
即$dp_i=dp_{k_i}+w(k_i,i)$。
而dp方程满足决策单调性指的是，决策点$k$随着$i$的增大保持单调不减。
即$k_1\le k_2 \le k_3 \le ...\le k_n$

四边形不等式证明决策单调性

至于如何判定$w$是否满足四边形不等式？我没学会也懒，其实一般也不用严谨证明啊（场上一般是打表或者感性理解的）

以下提供几个证明的blog
link1
link2

实现方法

以下提供两种实现方式

分治

使用条件：转移与枚举顺序无关

我们有转移方程：

\[dp_i=min_{j=1}^i js_{j}+w(j,i) \]

此处$js$的数组已知。

对于区间$[l,r]$，我们钦定$mid=(l+r)/2$

对于$[1,n]$，可以通过枚举$i\in[1,n]$来找到$k_{mid}$

然后考虑分治

因为$k_1\le ... \le k_{mid} \le ...\le k_n$

所以

当 $1\le i\le mid-1$ ，有 $1\le k_i \le k_{mid}$，所以通过枚举$[1,k_{mid}]$来找到新的$k$值
当 $mid-1\le i\le n$ ，有 $k_{mid}\le k_i \le n$，所以通过枚举$[k_{mid},n]$来找到新的$k$值

所以对于区间$[l,r]$，在$[k_{l-1},k_{r+1}]$中枚举，找到$k_{mid}$( 此时 $mid=(l+r)/2$ )，然后接着向下分治。

对于初始化，$k_0=1$，$k_{n+1}=n$

对于一个一维$dp$，其时间复杂度为$O(n \log n)$

然后套入本题，只需做$k$次分治，对于第$i$次，求出$dp[i][1]$~$dp[i][k]$，大力转移即可。
tips:时间复杂度为$O(n\log n k)$，不使用快读容易TLE

代码

#include<bits/stdc++.h>
using namespace std;
int a[4010][4010];
int sum[4010][4010];
int dp[4010][810];
int pos[4010];
int n,k;
inline int read()
{
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-')f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		x=(x<<1)+(x<<3)+(ch-'0');
		ch=getchar();
	}
	return x*f;
}
inline void write(int x)
{
	if(x<0)x*=-1,putchar('-');
	if(x>9)write(x/10);
	putchar(x%10+'0');
	return;
}
int val(int x,int y)
{
    return (sum[x][x]+sum[y][y]-sum[x][y]-sum[y][x])/2;
}
void fz(int j,int l,int r)
{
    if(l>r)
    {
        return ;
    }
    int ans=1e9,pans=0;
    int mid=(l+r)>>1;
    for(int i=pos[l-1];i<=pos[r+1];i++)
    {
        if(ans>dp[i][j-1]+val(mid,i))
        {
            ans=dp[i][j-1]+val(mid,i);
            pans=j;
        }
    }
    pos[mid]=pans;
    dp[mid][j]=ans;
    fz(j,l,mid-1);
    fz(j,mid+1,r);
}
int main()
{
    n=read();
    k=read();
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            a[i][j]=read();
            sum[i][j]=a[i][j]+sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
        }
    }
    for(int i=1;i<=n;i++)
    {
        dp[i][1]=val(0,i);
    }
    for(int j=2;j<=k;j++)
    {
        pos[0]=1;
        pos[n+1]=n;
        fz(j,1,n);
    }
    write(dp[n][k]);
    return 0;
}

二分队列

二分队列虽然较分治更难写，但其普适性更良好，当转移方程需要顺序求解时，即$$dp_i=min_{j=1}^i dp_{j}+w(j,i)$$
因为分治转移是乱序的，所以不能求解这种自转移方程，此时应该使用二分队列法。

类比决策单调性的定义，我们对于决策点$k$来说：
$k$是区间$[l,r]$的决策点，即对于任意$i\in [l,r]$，都有$dp_i=dp_{k}+w(k,i)$。

即称为$k$支配$[l,r]$。

考虑维护一个~~QED~~双端队列deque，队列中的元素为一个三元组$(k,l_k,r_k)$，表示$k$支配$[l_k,r_k]$。

初始时刻队列为空，考虑从小到大枚举$i$，对于$i$来说，要求出两个东西。

问题$i$的答案，即$dp[i]$的值
只考虑决策点$[1,i]$的情况下，对于区间$[1,n]$，$i$作为决策点时支配的区间$[l_i,r_i]$，并让其入队

考虑实现这个的过程

考虑队头
如果队头元素$(k,l_k,r_k)$中的$r_k<i$，说明$k$不是$i$及$i$之后的点的决策点，所以直接弹出；
反之若$r_k\ge i$，则将$l_k$赋值为$i$。
考虑队尾
如果$i$支配的区间不为空，对于决策点$[1,i]$，则一定会出现点$pos$，使$i$支配区间$[pos,n]$。
而根据决策单调性，支配区间$[i,pos)$的所有决策点一定都小于$i$。
考虑队尾元素$(k,l_k,r_k)$，若$dp[k]+w(k,l_k)>dp[i]+w(i,l_k)$，即用$i$转移$l_k$比$k$更优，根据决策单调性，区间$[l_k,r_k]$用$i$转移都比$k$更优，所以就可以将元素$(k,l_k,r_k)$弹出队尾。重复直至队列为空或该条件不成立。
添加元素
如果队列为空，即可直接将元素$(i,i,n)$加入队尾。
否则考虑队尾元素$(k,l_k,n)$，若$dp[k]+w(k,n)>dp[i]+w(i,n)$，说明$i$支配的区间不为空，其区间$[l_k,n]$中一定存在一个位置$pos$，使$k$支配的区间为$[l_k,pos)$，$i$支配的区间为$[pos,n]$，二分求解出$pos$的值，然后将$(k,l_k,n)$改为$(k,l_k,pos-1)$，将$(i,pos,n)$加入队尾即可。

由于需要二分，对于一个一维$dp$，其时间复杂度为$O(n \log n)$

然后再次套入本题，只需做$k$次二分队列即可。

tips:时间复杂度仍为$O(n\log n k)$，不使用快读容易TLE

代码

#include<bits/stdc++.h>
using namespace std;
const int inf=1e9;
struct jade
{
    int x,l,r;
}q[4010];
int a[4010][4010];
int sum[4010][4010];
int dp[4010][810];
int n,k;
inline int read()
{
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-')f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		x=(x<<1)+(x<<3)+(ch-'0');
		ch=getchar();
	}
	return x*f;
}
inline void write(int x)
{
	if(x<0)x*=-1,putchar('-');
	if(x>9)write(x/10);
	putchar(x%10+'0');
	return;
}
int val(int x,int y)
{
    return (sum[x][x]+sum[y][y]-sum[x][y]-sum[y][x])/2;
}
bool check(int pos,int i,int x,int j)
{
    return dp[x][j-1]+val(x,pos)>dp[i][j-1]+val(i,pos);
}
void efdl(int j)
{
    dp[0][j]=0;
    int l=1,r=0;
    r++;
    q[r].x=0;
    q[r].l=1;
    q[r].r=n;
    for(int i=1;i<=n;i++)
    {
        while(l<r&&q[l].r<i)
        {
            l++;
        }
        dp[i][j]=dp[q[l].x][j-1]+val(q[l].x,i);
        if(dp[q[r].x][j-1]+val(q[r].x,n)<=dp[i][j-1]+val(i,n))
        {
            continue;
        }
        while(l<r&&dp[q[r].x][j-1]+val(q[r].x,q[r].l)>dp[i][j-1]+val(i,q[r].l))
        {
            r--;
        }
        if(r<l)
        {
            r++;
            q[r].x=i;
            q[r].l=i;
            q[r].r=n;
            continue;
        }
        else
        {
            int ll=q[r].l;
            int rr=q[r].r+1;
            while(ll<rr)
            {
                int mid=(ll+rr)>>1;
                if(check(mid,i,q[r].x,j))
                {
                    rr=mid;      
                }
                else
                {
                    ll=mid+1;
                }
            }
            q[r].r=-1;
            r++;
            q[r].x=i;
            q[r].l=rr;
            q[r].r=n;
        }
    }
}
int main()
{
    n=read();
    k=read();
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            a[i][j]=read();
            sum[i][j]=a[i][j]+sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
        }
    }
    for(int i=1;i<=n;i++)
    {
        dp[i][1]=val(0,i);
    }
    for(int j=2;j<=k;j++)
    {
        efdl(j);
    }
    write(dp[n][k]);
    return 0;
}

tips:注意判断二分边界以及队内是否有元素。

en...终于码完决策单调性了

wqs二分

首先明确一下

wqs二分解决的问题是：在$n$个物品中恰好选择$k$个，求权值的最大或者最小值。

状态转移方程形如$$dp[i][k]=min(dp[j][k-1]+w(j,i))$$

wqs二分使用的条件是：设$f(i)$为选$i$个物品的答案，将所有$(i,f(i))$的点画在坐标系中并连线，会组成一个凸壳（此时斜率为单调的）。

以下是手模样例

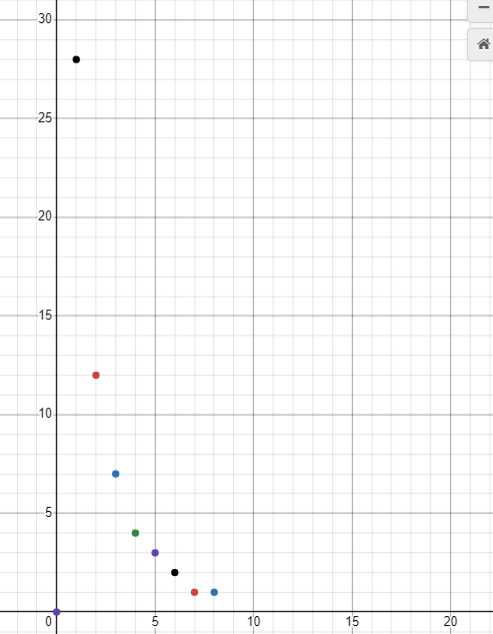
qwq它好像是个减函数？？

wqs二分解决问题的特点：如果不限制选的个数，很容易求出答案；选的物品越多。权值越大/越小。

使用过程
wqs二分，顾名思义其中一定包括二分。

让我们先不考虑$k$的限制，二分出一个$mid$表示选一次物品（即进行一次转移）的附加权值。

我们发现，选的次数越多，其附加权值越大。
对于下凸壳来说，当最优方案选的物品次数大于$k$时，就增大$mid$，否则减小$mid$。

对于上凸壳来说，当最优方案选的物品次数小于$k$时，就增大$mid$，否则减小$mid$。

最后答案去掉$mid\times 选择次数$就行。

然后是二分的$check$部分（即使用$DP$求解答案）
我们先考虑一个上凸壳（取max操作）(反之，下凸壳对应取min操作）

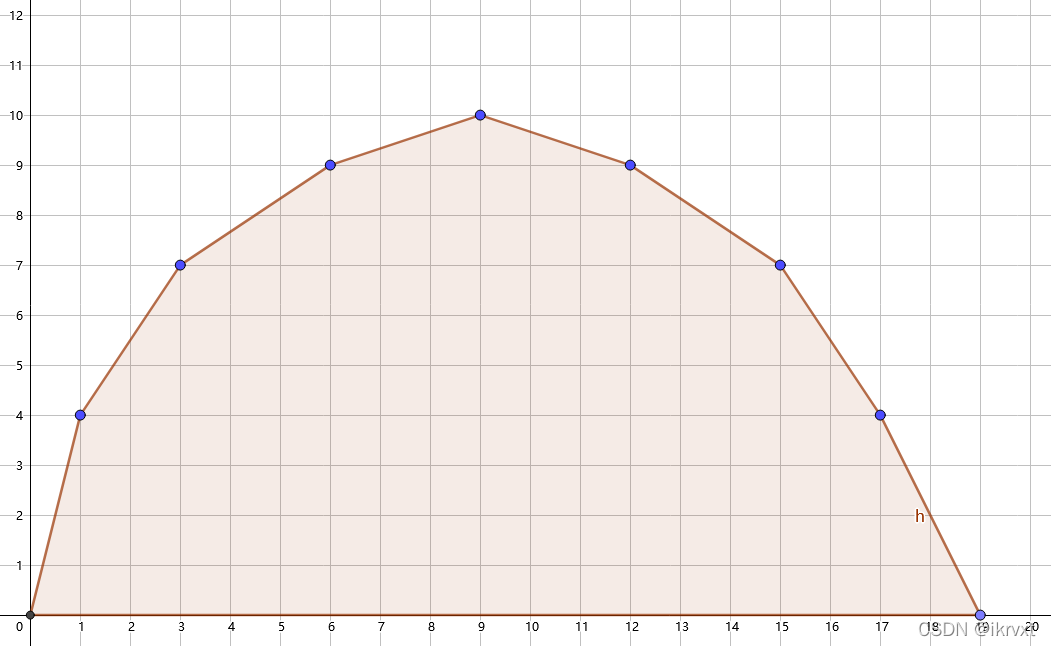
重新明确下一个点$(x,y)$的定义：$x$表示选了$x$次物品，$y$表示选择$x$得到的最优答案。

显然只需求出当$x=k$时$y$的值。
但如果朴素去做时间复杂度太劣了，所以我们利用凸壳的优良性质：斜率是单调的

即考虑使用直线去切凸壳

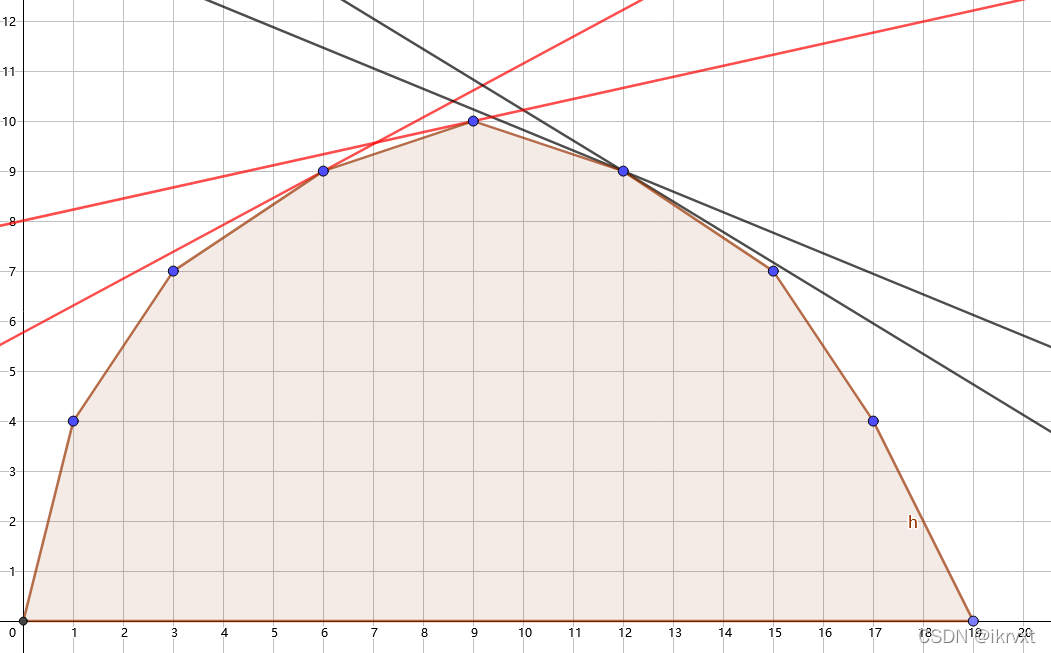
由单调性可知，我们可以通过调整直线的斜率，来改变直线截距$b$最大时切到的点，这个点可以表示选$x$次得到的答案。
对于这个上凸壳来说，当斜率越小时，切到的点越靠右。

此时我们做一个对应，发现之前二分得出的每次选择物品的附加值$mid$就是直线的斜率取反。
考虑直线$y=kx+b$，$k=-mid$是每次选择物品的附加值取反，$x$是物品的选择次数，$y$是对于选$x$次的答案。
即我们考虑，由于是求最大值，应减去额外贡献才能让分段越多代价越大（反之，如果求的是最小值，就加上额外贡献，即$k=mid$）。

（也可以通过凸壳斜率单调的这个性质考虑二分正确性）。

我们考虑$b$是什么，$b=y-kx$，即选一次物品的附加值为$-k$，选了$x$次物品，当原本的答案为$y$时，$b$就是对于附加值为$-k$来说，选择$x$次对应的答案，即规定附加值为$-k$时，做$dp$的答案。
当我们可以求出$b$时，$y$也随之出现了。

观察下图，我们发现，

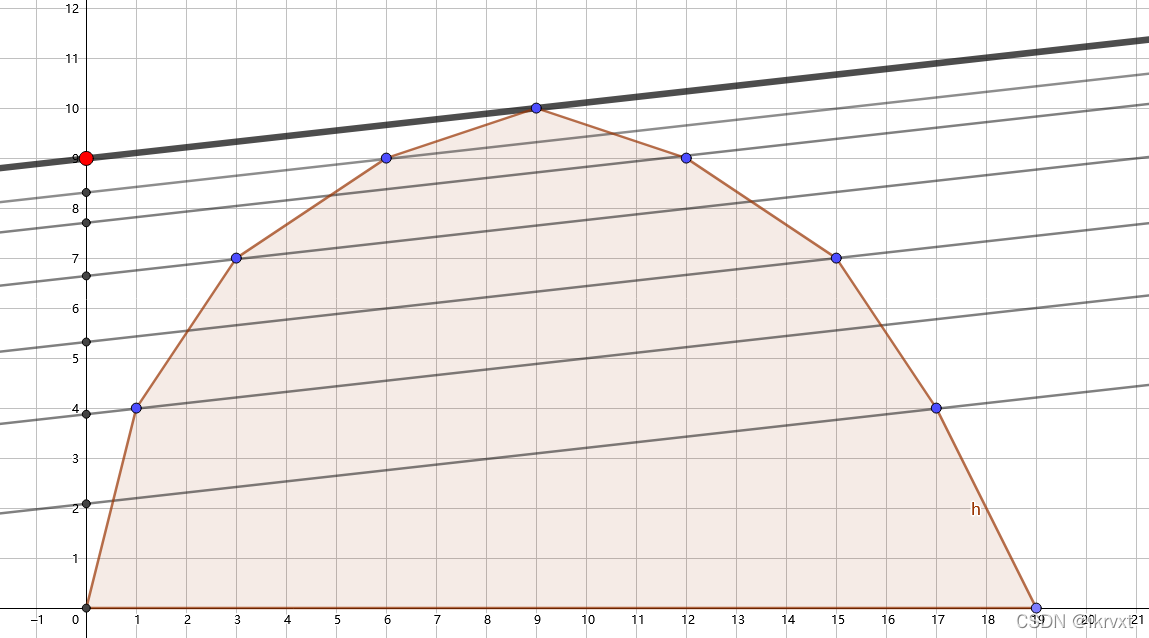
当以附加值为$-k$转移时，$dp$的答案（此时是取max）和截距$b$是一一对应的。

此时通过$dp$求出$b$的值，在过程中可以记录转移次数，然后返回判断与$k$的大小（要求次数），如果正好等于$k$，就将求出的$b$（max）转回为$y$，此时$y$就是答案。

回到开头，我们发现，我们没有考虑遍历$k$，而是使用二分替代，$dp$维数减了一维，状态转移方程变为$$dp[i]=min(dp[j]+w(j,i))$$
只需要二分附加值，做$\log值域$次$dp$。

时间复杂度为$O(n^2 \log V)$，比原复杂度$O(n^2 k)$更优。

回归题目

发现原状态转移方程是$O(n^2 k)$的，但它具有决策单调性且答案函数是一个下凸壳，可以使用wqs二分套决策单调性优化DP来优化时间复杂度。

具体的，我们先使用wqs二分去除题目中$k$个座舱的限制（即将二维DP转化为一维DP），然后内层DP（即二分的check函数）使用决策单调性优化。

需要注意的是，此时转化后的一维DP转移方程是一个自转移方程，所以只能使用二分队列法来实现

时间复杂度为优秀的$O(n \log n \log V)$，不使用快读也可以通过本题。

细节参见代码

代码实现

#include<bits/stdc++.h>
using namespace std;
const int inf=1e9;
struct jade
{
    int x,l,r;
}q[4010];
int a[4010][4010];
int sum[4010][4010];
int dp[4010];
int cnt[4010];
int n,k;
int val(int x,int y)
{
    return (sum[x][x]+sum[y][y]-sum[x][y]-sum[y][x])/2;
}
bool check(int pos,int i,int x)
{
    return dp[x]+val(x,pos)>dp[i]+val(i,pos);
}
void efdl(int fjz)
{
    dp[0]=0;
    cnt[0]=0;
    int l=1,r=0;
    r++;
    q[r].x=0;
    q[r].l=1;
    q[r].r=n;
    for(int i=1;i<=n;i++)
    {
        while(l<r&&q[l].r<i)
        {
            l++;
        }
        dp[i]=dp[q[l].x]+val(q[l].x,i)+fjz;
        cnt[i]=cnt[q[l].x]+1;
        if(dp[q[r].x]+val(q[r].x,n)<=dp[i]+val(i,n))
        {
            continue;
        }
        while(l<r&&dp[q[r].x]+val(q[r].x,q[r].l)>dp[i]+val(i,q[r].l))
        {
            r--;
        }
        if(r<l)
        {
            r++;
            q[r].x=i;
            q[r].l=i;
            q[r].r=n;
            continue;
        }
        else
        {
            int ll=q[r].l;
            int rr=q[r].r+1;
            while(ll<rr)
            {
                int mid=(ll+rr)>>1;
                if(check(mid,i,q[r].x))
                {
                    rr=mid;
                }
                else
                {
                    ll=mid+1;
                }
            }
            q[r].r=rr-1;
            r++;
            q[r].x=i;
            q[r].l=rr;
            q[r].r=n;
        }
    }
}
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin>>n>>k;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            cin>>a[i][j];
            sum[i][j]=a[i][j]+sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
        }
    }
    for(int i=1;i<=n;i++)
    {
        dp[i]=val(0,i);
    }
    int l=0,r=sum[n][n];
    while(l<r)
    {
        int mid=(l+r)>>1;
        efdl(mid);
        if(cnt[n]>k)
        {
            l=mid+1;
        }
        else
        {
            r=mid;
        }
    }
    efdl(r);
    cout<<dp[n]-r*k;
    return 0;
}

但不关流同步也会大T特T

也许是 ${\cal {The }}$ ${\cal {end. }}$

posted @ 2026-01-15 20:16 BIxuan—玉寻阅读(12) 评论(3) 收藏举报

刷新页面返回顶部

${\scr {jade }}$ ${\scr {seek }}$

一只微醺鱼鱼

CF321E Ciel and Gondolas || 决策单调性 wqs二分优化DP 学习笔记

分析题目

前置知识

决策单调性优化DP（四边形不等式优化DP）

概念以及相关证明

实现方法

分治

代码

二分队列

代码

wqs二分

回归题目

代码实现

也许是 \({\cal {The }}\) \({\cal {end. }}\)

公告

${\scr {jade }}$ ${\scr {seek }}$

一只微醺鱼鱼

CF321E Ciel and Gondolas || 决策单调性 wqs二分 优化DP 学习笔记

分析题目

前置知识

决策单调性优化DP（四边形不等式优化DP）

概念以及相关证明

实现方法

分治

代码

二分队列

代码

wqs二分

回归题目

代码实现

也许是 \({\cal {The }}\) \({\cal {end. }}\)

公告

CF321E Ciel and Gondolas || 决策单调性 wqs二分优化DP 学习笔记