CSP-S模拟36 2025.10.21（20230903炼⽯计划NOIP模拟赛1）

a o e i u ü
b p m f d t n l g k h j q x zh ch sh z c s

A. 岛屿

题面link

赛时

一眼期望概率，扔惹。

赛后&&正解

咳咳，以下思路和言论来自机房大蛇魔法少女

我只是记录一下！不是我说的！！！

考虑题目给出的第一个有用的样例
rtttttttttttttttttt:

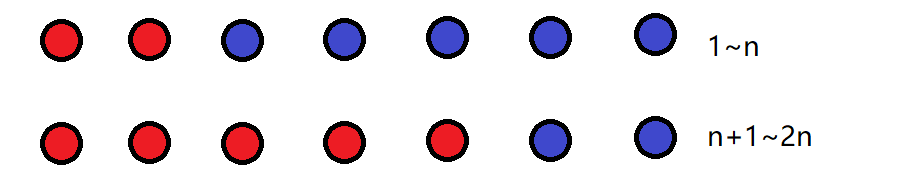
按题目方式连边：

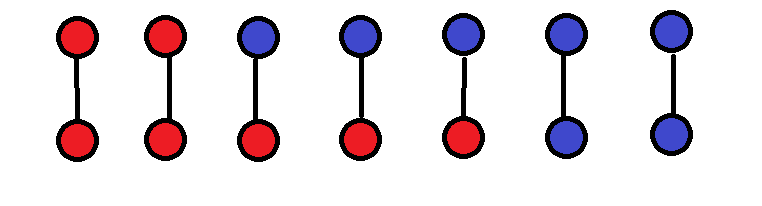
太恶心了！！移动一下它们的位置。

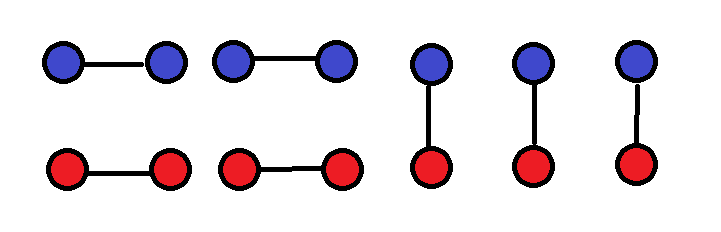
它们 ——> 他/她们
rt:
将以下结构命名为“成年人”和“儿童” (\(x\)个成年人\(y\)个儿童）

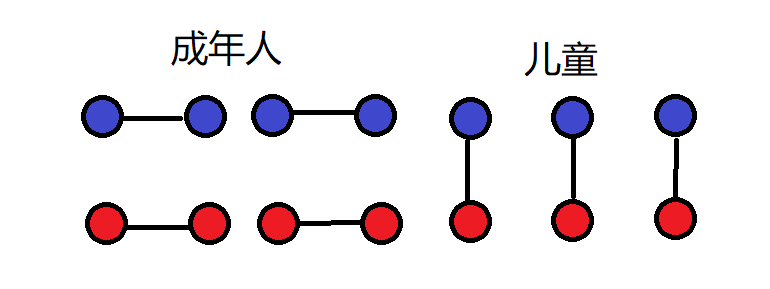
考虑先连（杀）儿童：

情况一：
自~ 己~ 连~ 自~ 己~（他管这个叫“水仙”）

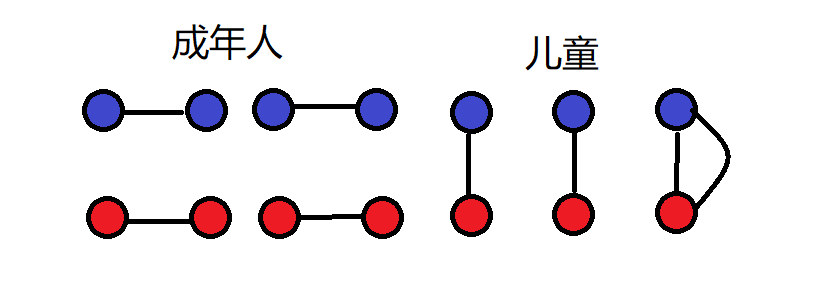
形成了一个连通块，然后他就不能连边了，他死啦~
这是有贡献的死，我们把这个叫做好死法

情况二：
自~ 己~ 连~ 儿~ 童~（他管这个叫“***”）

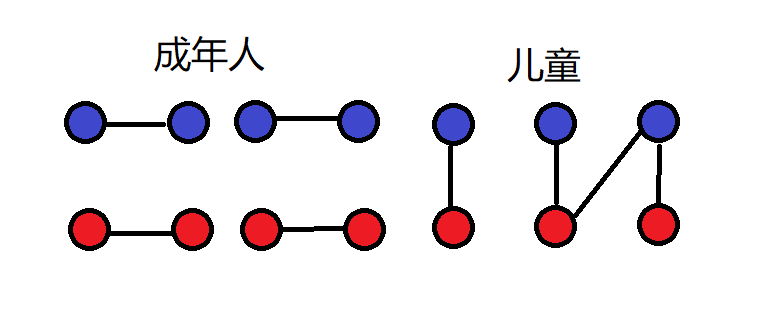
没有形成一个连通块，但他不能连边了，因为他被合并了，他死啦~
这是没有贡献的死，我们把这个叫做坏死法

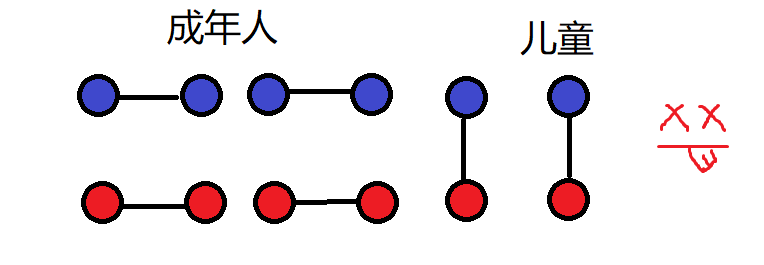
情况三：
自~ 己~ 连~ 成~ 人~（他管这个叫“***”）

同上，坏死法

所以儿童有两种死法，每次死掉一个儿童，是好死法（有贡献）的概率是：

\[\frac{1}{当前儿童数+当前成人数 \times 2} \]

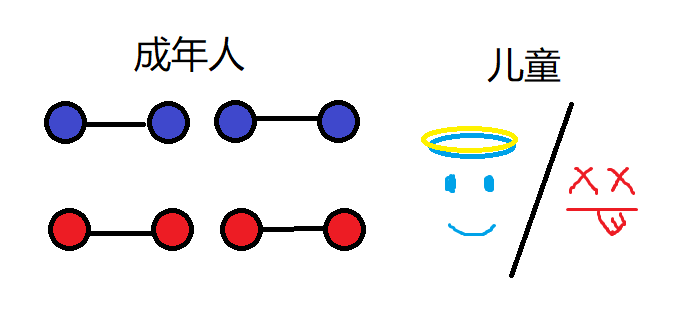
考虑再连（杀）成年人：

可以先钦定该边被连
（因为第一条边无论如何连都可以通过移动人的位置变成这样的连法）

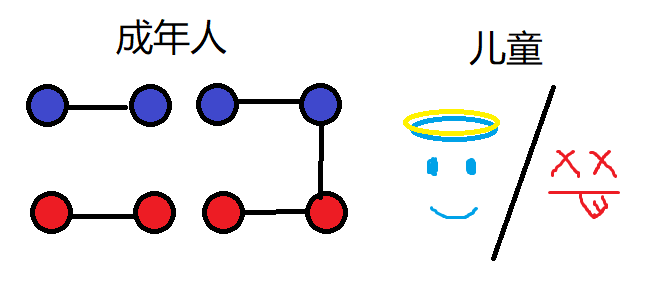
情况一：
自~ 己（的）~ 连~ 自~ 己（的）~（他管这个叫“***”）

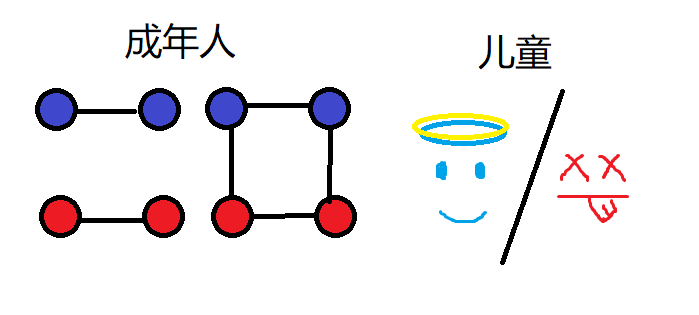
有贡献，是好死法

情况二：
自~ 己（的）~ 连~ 别~ 人（的）~（他管这个叫“***”）

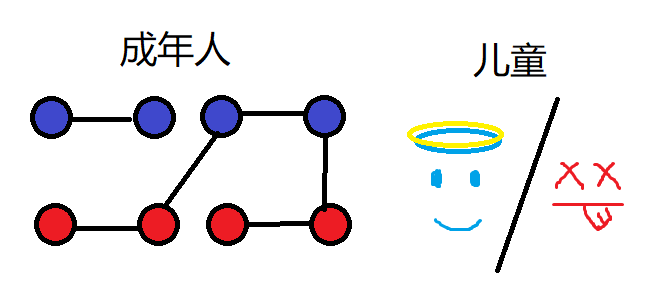
没贡献，是坏死法。

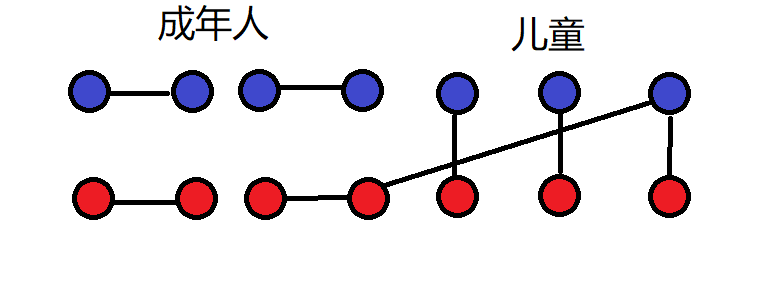
以下是另一种情况二：

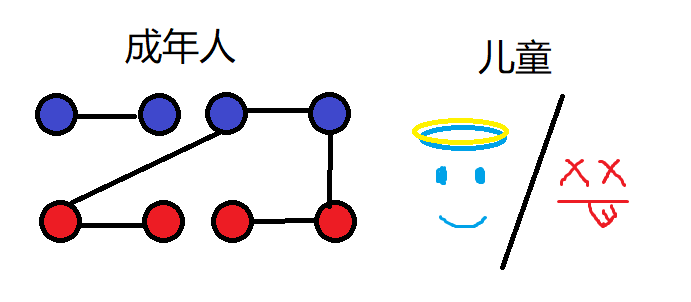
同样没贡献，是坏死法。

所以成年人有两种死法，每次死掉一个成年人，是好死法（有贡献）的概率是：

\[\frac{1}{当前成人数 \times2-1} \]

一个一个杀，就杀光啦哈哈哈哈哈哈哈哈哈哈哈

代码

#include<bits/stdc++.h>
using namespace std;
int x,y;
int tot=1; 
double ans;
int main()
{
	freopen("island.in","r",stdin);
	freopen("island.out","w",stdout);
    cin>>x>>y;
    for(int i=y;i>0;i--)
	{
		ans+=1.0/(i+x*2);
	} 
	for(int i=x;i>0;i--)
	{
		ans+=1.0/(i*2-1);
	}
	printf("%.10lf",ans);
    return 0;
}

后记

魔法少女有更为抽象的写法（我不敢血怕被ban）
挂一个链吧link(有点子雷人qwq)

B. 小朋友

题面link

赛时

DP->贪心->暴力->唐必
不想多说这是个坏死法

赛后

改改改，糖糖糖

1.0

神秘折半搜索
发现\(n \le 50\)，\(50/2=25\)，\(2 ^{25}=33554432\)
明显可过。
即枚举答案的长度，考虑对每个长度做折半搜索（一半\(s\),一半\(t\)），从\(z\)到\(a\)遍历是否可以放在这一位。
判断条件：

• 若为\(s\)那一半
  s的那一位是遍历到的字符
• 若为\(t\)那一半
  t的那一位是遍历到的字符,s的那一位是答案记录的那个字符

tips:\(t\)那一半记得判误解，即代码中的“肝·神祇变量·OIer·硬化·悲伤蛙一世”（嘻嘻嘻嘻嘻）

代码

#include<bits/stdc++.h>
using namespace std;
string s,t,ans[55];
int len,js;
string dfs1(int x,string jade)
{
    if(jade.size()>=js)
	{
        return jade;	
	}	
	for(int i=26;i>=1;i--) 
	{
		char c='a'+i-1;
		int y=s.size()-js+jade.size();
		for(int j=x;j<=y;j++)
		{
		    if(s[j]==c)
			{
			    return dfs1(j+1,jade+c);
			}	
		}
	}
} 
string dfs2(int x,string seek)
{
    if(seek.size()>=js)
	{
        return seek;	
	}
	for(int i=26;i>=1;i--) 
	{
		char c='a'+i-1;
		int y=s.size()-js+seek.size();
		for(int j=x;j<=y;j++)
		{
		    if(t[j]==c&&ans[js][seek.size()]==s[j])
			{
			    string gyh=dfs2(j+1,seek+c);
			    if(gyh!="gan_shen_qi_bian_liang_OIer_ying_hua_bei_shang_wa_yi_shi")
			    {
			    	return gyh;
				}
			}	
		}
	}
	return "gan_shen_qi_bian_liang_OIer_ying_hua_bei_shang_wa_yi_shi" ;
} 
int main()
{
	freopen("xiao.in","r",stdin);
	freopen("xiao.out","w",stdout);
	cin>>s>>t;
	int len=s.size();
	for(int i=1;i<=len;i++)
	{
		js=i;
		ans[i]=dfs1(0,"");
		ans[i]+=dfs2(0,"");
	}
	sort(ans+1,ans+1+len);
	cout<<ans[len];
	return 0;
} 

2.0

神奇的DP!
DPDPDPDPDPDPDPDPDPDPDPDPDPDPDPDPDPDPDPDPDPDPDPDPDPDPDPDPDPDPDPDPDPDPDP
设\(dp[i]\)为长度为\(i\)的字典序最大的字符串
分设\(dps\)和\(dpt\)考虑倒序刷表，外层枚举遍历到\(s\),\(t\)的哪个字符，内层枚举将这个字符放在哪个位置上，注意遍历顺序

代码

#include<bits/stdc++.h>
using namespace std;
string s,t;
string dps[55],dpt[55],ans;
int main()
{
    freopen("xiao.in","r",stdin);
	freopen("xiao.out","w",stdout);
    cin>>s>>t;
    s='0'+s;
    t='0'+t;
	for(int i=1;i<=s.size();i++)
	{
	    for(int j=i;j>=1;j--)
	    {
	    	string x=dps[j]+s[i];
	    	string y=dpt[j]+t[i];
	    	if(x>dps[j+1])
	    	{
	    		dps[j+1]=x;
	    		dpt[j+1]=y;
			}
			else if(x==dps[j+1]&&y>dpt[j+1])
			{
			    dpt[j+1]=y;
			} 
		}
	} 
	for(int i=1;i<=s.size();i++)
	{
		ans=max(ans,dps[i]+dpt[i]);
	}
	cout<<ans; 
    return 0;	
} 

等等等等等等等等没改完