（薛定谔のCSP-S）模拟35 2025.10.20

咕掉好几场墨泥塞的僵尸来颓题解惹
因为想等大 ~蛇 ~们 ~改完之后再改（根本不会）

rt：
你说这是吃薯片-S?
我还是跳楼来的比较快。
这题太**的神秘了，看上去都可做实际上（我）都写不出来。
sssssssssssssad。

A. 集合

题面link
开题！T1就是图论吗？T1就是图论吗？T1就是图论吗？T1就是图论吗？T1就是图论吗？T1就是图论吗？T1就是图论吗？

不是，T1是个结论！！！！！！

哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈

咳咳。

赛时

手玩2.5h，发现一个神秘的性质：
rt:
将1，2结盟

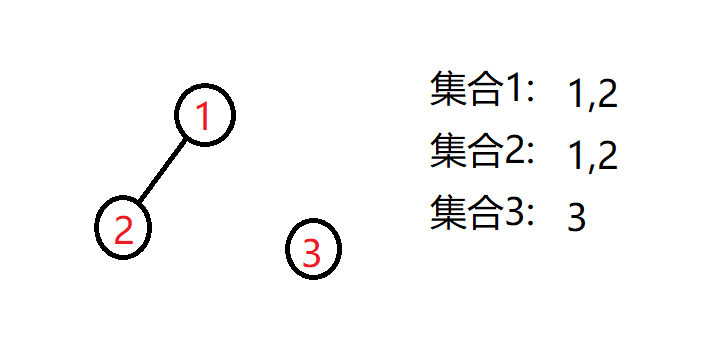
将1，3结盟

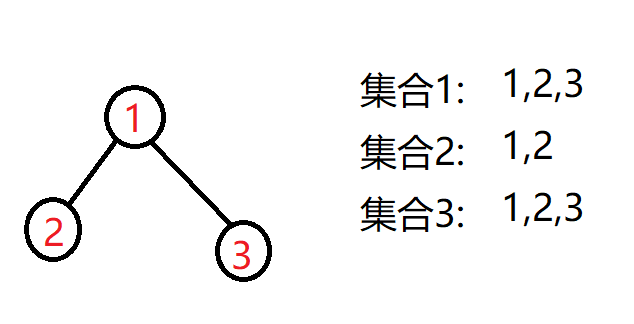
将1，2结盟

发现在$1,2,3$随意连边，发现最大的集合大小为连通块大小，然后你考虑非最大的集合，发现其可以通过过倒着遍历加边来处理集合大小。
然后。。
发现你不能合理的处理这个东西
死了。┏┛墓┗┓...(((m-__-)m

赛后

根据题解可知：
若你倒着按输入连边，可以得到 $i$ 出现在哪些集合里面（手玩一下可得)，且与集合大小是相等的，然后你打开高一数学课本，发现：

\[|S ∪ T| = |S| + |T| − |S ∩ T| \]

然后可以发现，若你连一个边，可能会有以下两种情况：

之前这条边没有被连过
那这两个集合一定没有公共元素，所以它们两个的交集大小是他们的大小之和。连完之后可得两个集合的交集大小是它们的集合大小
之前这条边有被连过
那这两个集合一定有公共元素，所以它们两个的交集大小是他们的大小之和减去他们的并集大小。
考虑他们的并集大小就是上一次连这条边得到的集合大小。

好！然后就模拟一下啊！
唔，等等

考虑如何证明一下这个东西

若你倒着按输入连边，可以得到 $i$ 出现在哪些集合里面（手玩一下可得)，且与集合大小是相等的

数学归纳法 😃(bushi)

因为你正着连边使$x,y$结盟，可以知道$x,y$这两个集合包含了哪些元素，即结盟的对方互相将元素传递过去，集合$x$是等于集合$y$的，若你再使$y,z$结盟，则集合$y$等于集合$z$，且$x\subseteq y=z$。$x$中的元素都出现在$y,z$之中。
考虑反向连边，发现$z\subseteq y=x$,即$y,z$中的元素都出现在$x$之中，传递是相反的，将做法扩展一下即可证出$x$的元素就是$x$出现在哪些集合里面。
所以$x$的集合大小就是$x$出现在了几个集合里。

不太严格，可以自己手动连边推一下。

代码

#include<bits/stdc++.h>
using namespace std;
int x[400010],y[400010];
int to[400010],siz[400010],last[400010];
bool vis[400010];
int main()
{
	freopen("set.in","r",stdin);
	freopen("set.out","w",stdout);
	int n,m;
	cin>>n>>m;
	for(int i=1;i<n;i++)
	{
	    cin>>x[i]>>y[i];	
	} 
	for(int i=1;i<=m;i++)
	{
		cin>>to[i];
	}
	for(int i=1;i<=n;i++)
	{
		siz[i]=1;
	}
	for(int i=m;i>=1;i--)
	{
		int js=to[i];
		if(vis[js]==0)
		{
			siz[x[js]]=siz[y[js]]=siz[x[js]]+siz[y[js]];
			last[js]=siz[x[js]];
		}
		else
		{
			siz[x[js]]=siz[y[js]]=siz[x[js]]+siz[y[js]]-last[js];
			last[js]=siz[x[js]];
		}
		vis[js]=1;
	}
	for(int i=1;i<=n;i++)
	{
		cout<<siz[i]<<" ";
	}
	return 0;
}

B. 存钱

题面link
大大大大大大大大工程！

赛时

观察题面，发现$k$有两个取值：$k=n-1$,$k=n-2$。
考虑数据点分治（大雾）
遇到这种疑似可能也许是猜结论题怎么办？
让我们！
手玩一组样例；
rt:

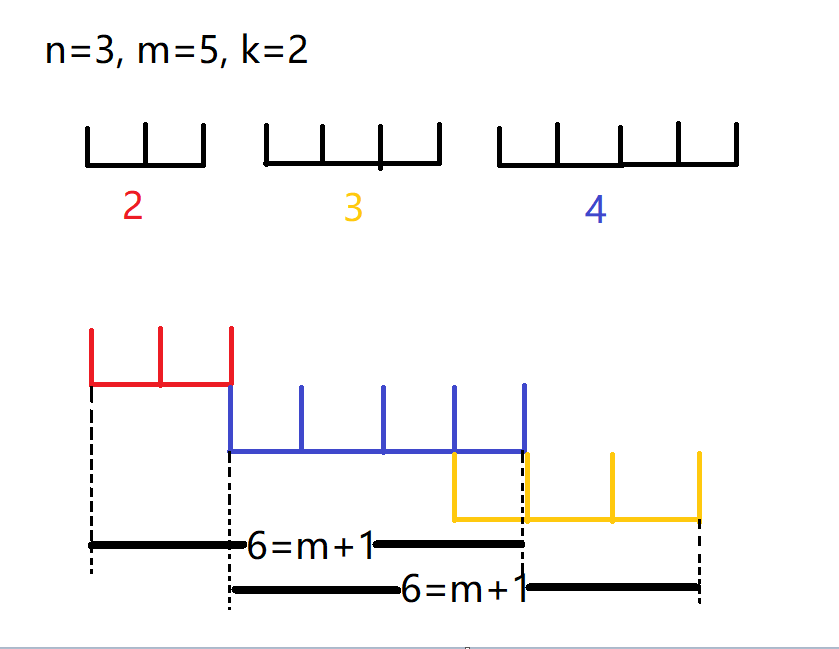
发现若$k=n-1$：

则题意可以转化为给你$n$条线段，将其拼起来，可以重叠，但每两条拼在一起的线段的长度要大于$m$(即满足任意一个长为 $m$ 的区间都最多只包含一个完整线段)，最小化线段拼接起来的总长度。

简单题，发现两条拼在一起的线段的长度为$m+1$是最优的，设其一条线段的长度是$x$,另一条线段的长度是$y$，则其重叠部分的的长度是$x+y-m-1$。

对于$n$段线段相接来说，若要最小化其长度，就要使重叠部分最长，即最大化$\sum x+y-m-1$。

发现对于$n$条线段拼接起来，其重叠部分有$n-1$段，考虑$n$条线段的贡献，发现除第$1$条和第$n$条有一次贡献外，其余的都对重叠部分的长度有两次贡献。

因为$m+1$是一个定值，所以要最大化$\sum x+y$。

将线段长度排序，将最短的两条线段放在两端，然后计算答案即可。

$k=n-2$死活不知怎么做。

赛后

呃呃呃呃呃呃呃呃呃呃呃呃呃神秘做法啊哈哈哈哈哈哈哈哈哈

😦 它把$k=n-2$拆成两个了？？？
好像这辈子也想不出。。

即将$n$条线段化分为两个部分，分别做 $k = n − 1$ 的部分，最后将线段拼起来。这样做一定满足任意一个长为 $m$ 的区间都最多只包含两个完整线段，因为两部分每个部分都最多只包含一个完整线段。

不知如何证明其正确性，直接粘题解：

以下引自题解

假如我们定好了一个合法方案中每个区间的覆盖范围。
如果两个区间会被一个长为 $m$ 的区间同时包含，我们就在这两个区间之间连一条边。
显然图不可能出现大小大于等于 $3$ 的环，否则就能找到区间同时包含这些区间。
那么原图一定可以被二染色。
也就是分成两个点集，每个点集内部没边。
这样就一定对应了两个 $k = n − 1$ 的问题。
也就是说，上面的做法是充要的。

好的好的好的。

以下是做法：

首先去掉长度最小的四个线段，它们一定会被放在首尾无贡献。

那我们假设全集是 $U$，我们将区间划分为集合 S 和集合 $U − S$，令 $b_i = m + 1 − a_i$，那么答案就是 $m + 1 + max(∑_{x∈S}b_x,∑_{x∈/S}b_x)$

考虑将 $b$ 从小到大排序，找到最后一个位置 $pos$ 使得 $∑^{pos}_{i=1}b_i ≤\frac{sum}{2}$ 。

先选上所有 $pos$ 之前的元素，此时的总和与$\frac{sum}{2}$差值不超过 $m$。

如果我们此时进行调整，在总和比 $\frac{sum}{2}$ 大时去掉 $pos$ 之前选的某个值，在总和比 $\frac{sum}{2}$ 小的时候加入 $pos$ 之后的某个值，那么我们调整过程中出现的值与 $\frac{sum}{2}$差值都不会超过$ m$。

我们从 $pos$ 到 $n$ 进行调整，加入当前的值或者删除 $pos$ 之前的值。

考虑一个 $dp$，设 $f[i][j]$ 表示调整到 $i$，要想凑出来 $j +\frac{sum}{2}$，左端点至少在哪里（也就是删除的数都在 $f[i][j]$ 右边）。
没有就是 $0$。

根据上文有 $−m ≤ j ≤ m$。转移枚举当前值是否加入，在考虑 $pos$ 左侧新增的能删值是否删除。

可以滚动数组。

代码

#include<bits/stdc++.h>
using namespace std;
int n,m,k,maxx,a[20005],b[20005],js[20005];
int f[20005],g[20005],res;
void solve()
{
	memset(f,0,sizeof(f));
	memset(g,0,sizeof(g));
	cin>>n>>m>>k;
	int nn=n;
	for(int i=1;i<=n;i++)
	{
    	cin>>a[i];	
	}
	sort(a+1,a+1+n);
	maxx=a[n];
	while(n&&a[n]>m)
	{
	    n--;	
	}
	if(k==nn-1)
	{
		int ans=m+1;
		for(int i=3;i<=n;i++)
		{
			ans+=m+1-a[i];
		}
		cout<<max(ans,maxx)<<endl;
		return ;
	}
	if(n<=2)
	{
	    cout<<maxx<<endl;
		return;
	}
	if(n<=4)
	{
	    cout<<max(maxx,m+1)<<endl;
		return;
	}
	int tot=0;
	for(int i=5;i<=n;i++)
	{
        tot++;
	    js[tot]=m+1-a[i];
	}
	n=tot;
	sort(js+1,js+1+n);
	int sum=0;
	for(int i=1;i<=n;i++)
	{
		sum+=js[i];
	}
	int pos=1,ans=0;
	while(pos<=n&&ans+js[pos]<=sum/2)
	{
		ans+=js[pos];
		pos++;
	}
	g[ans-sum/2+10000]=pos;
	for(int i=pos;i<=n;i++)
	{
		memcpy(f,g,sizeof(f));
		for(int j=0;j<=9999;j++)
		{
			f[j+js[i]]=max(f[j+js[i]],g[j]);
		}
		for(int j=20000;j>=10001;j--)
		{
			for(int kk=g[j];kk<f[j];kk++)
			{
				f[j-js[kk]]=max(f[j-js[kk]],kk);
			}
		}
		memcpy(g,f,sizeof(g));
	}
	for(int i=10000;i>=0;i--)
	{
		if(f[i])
		{
		    res=sum/2-10000+i;
		    break;
		}
	}
	cout<<max(maxx,m+1+sum-res)<<endl;
}
int main()
{
	freopen("money.in","r",stdin);
	freopen("money.out","w",stdout);
	int T;
	cin>>T;
	while(T--)
	{
	    solve();	
	}
	return 0; 
}

等等等等等等等等我没改完

posted @ 2025-10-20 18:54 BIxuan—玉寻阅读(23) 评论(5) 收藏举报

刷新页面返回顶部

${\scr {jade }}$ ${\scr {seek }}$

一只微醺鱼鱼

（薛定谔のCSP-S）模拟35 2025.10.20

A. 集合

赛时

赛后

代码

B. 存钱

赛时

赛后

代码

等等等等等等等等我没改完

公告