2025多校冲刺CSP模拟赛2 2025.10.4 模拟炸

rt:炸了

T1 查询

题面

赛时

疯狂排序！！疯狂贪心！！疯狂分讨！！疯狂星期四六！！（大雾）
无果。死了。
打了暴力32pts遗憾离场

正解

二分答案！闪亮登场！
考虑比较元素为\(a_i+b_i*c_j\)形如一次函数\(y=kx+b\),
即设\(k=b_i,b=a_i,x=c_j\),则对\(y\)进行查找。
rt:

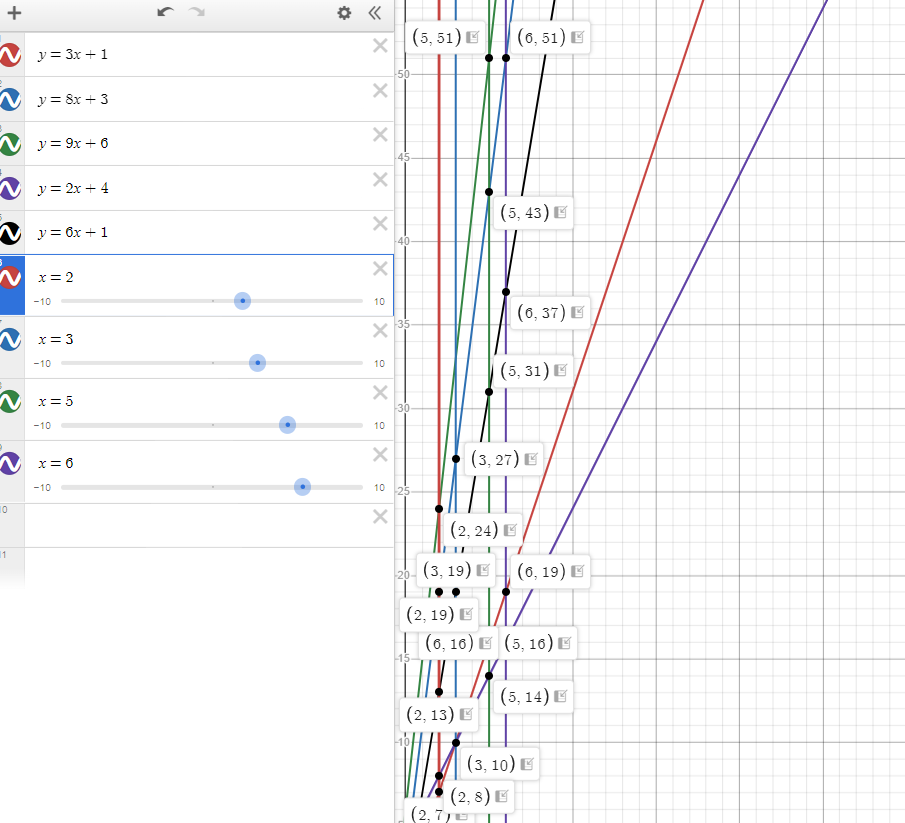
发现：若\(k=b_i,b=a_i\)为定值，则\(x=c_j\)越大，\(y\)越大。

观察数据范围，考虑对答案二分（即第\(k\)大的数为\(js\)），check是否有\(k\)个数小于\(js\)。

如何check?
根据上面的发现，对\(c\)数组进行排序，使其具有单调性，再次进行二分答案，对于每个\(a_i，b_i\)，二分答案（可调upper_bound）有多少个\(c_j\)使\(a_i+b_i*c_j \le js\),然后累加比较是否大于等于\(k\)。
时间复杂度：\(O(n \log n \log V)\)。

代码：

#include<bits/stdc++.h>
using namespace std;
long long a[100010],b[100010],c[100010];
int n;
long long k;
bool check(long long js)
{
	long long res=0;
    for(int i=1;i<=n;i++)
	{
	    long long dk=(upper_bound(c+1,c+n+1,(js-a[i])/b[i])-c-1);
		res+=dk;	
		if(res>=k)
		{
		    return 1;
		}	
	} 
	if(res>=k)
	{
	    return 1;
	}
	return 0;
}
int main()
{
	ios::sync_with_stdio(false);
	freopen("query.in","r",stdin);
	freopen("query.out","w",stdout);
    cin>>n;
    for(int i=1;i<=n;i++)
	{
		cin>>a[i];
    }
	for(int i=1;i<=n;i++)
	{
	    cin>>b[i];	
	} 
	for(int i=1;i<=n;i++)
	{
		cin>>c[i];
	}
	cin>>k; 
    sort(c+1,c+1+n);
	long long l=0,r=1e18,mid;
    while(l<r)
	{
	    mid=(l+r)>>1;
	    if(check(mid))
	    {
	    	r=mid;
		}
		else
		{
			l=mid+1;
		}
	} 
	cout<<r;
	return 0;
} 

T2 参加

题面

赛时

10min烧烤性质！！20min证明性质！！疯狂证明！！疯狂证明！！疯狂证明！！

5min写出代码！！计算时间复杂度！！疯狂TLE！！疯狂TLE！！疯狂TLE！！

评价：不如暴力

打了不如暴力25pts遗憾离场
（其实应该是40pts，但唐必僵尸没开long long,且极大值调用的INT_MAX导致挂掉15pts）

40pts

思考：
以\(k\)的左边部分为例，发现若相邻两个数之间不满足严格递增（即\(a_i \ge a_{i+1}\)）
其一定会有\(x\)次操作\([l,r]\),不同时包含\(a_i,a_{i+1}\)(即\(l \le i \le r <i+1\))
此时\(x=a_i-a_{i+1}+1\),\(x\)即为对答案的贡献。
做法：
枚举分界点\(k\),将序列分为两部分
左边严格上升，右边严格下降
两部分分别遍历,对于相邻数字\(a_i,a_{i+1}\)，若其不符合它所处部分的规则，它对答案的贡献为两数差值加一（因为是严格上升或下降)
最终答案是对于一个\(k\),其两部分的贡献取较大值,然后对于每个k取较小值。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
long long a[200010];
int main()
{
	ios::sync_with_stdio(false);
	freopen("attend.in","r",stdin);
	freopen("attend.out","w",stdout);
	long long n;
	cin>>n;
	for(long long i=1;i<=n;i++)
	{
	    cin>>a[i];	
	}	
	long long res=99999999999999; 
    for(long long k=1;k<=n;k++)
	{
		long long ans1=0,ans2=0;
	    for(long long i=1;i<k;i++)
		{
		    if(a[i]>=a[i+1])
			{
			    ans1+=a[i]-a[i+1]+1; 
			}	
		}  
		for(long long j=n;j>k;j--)
		{
		    if(a[j]>=a[j-1])
			{
			    ans2+=a[j]-a[j-1]+1; 
			}	
		} 
		res=min(res,max(ans1,ans2));
		if(res==0)
		{
		    cout<<0;
			return 0;	
		} 
	}
	cout<<res;
	return 0;
}

正解

发现其性质是优的，只是会TLE

我们考虑优化：
发现对于每次枚举\(k\)为分界点时，都计算了相邻数字\(a_i,a_{i+1}\)对答案的贡献，有许多冗杂计算浪费时间。

如何优化:
可以使用差分的方法
用一个差分数组\(cf\)记录相邻数字\(a_i,a_{i+1}\)的差
再用前缀和数组\(prv\)和后缀和数组\(nxt\)还原答案
最后再枚举分界点，找出答案。

代码

#include<bits/stdc++.h>
using namespace std;
long long a[200010],cf[200010];
long long prv[200010],nxt[200010];
long long ans=1e18;
int n;
int main()
{
	ios::sync_with_stdio(false);
	freopen("attend.in","r",stdin);
	freopen("attend.out","w",stdout);
    cin>>n;
	for(int i=1;i<=n;i++)
	{
	    cin>>a[i];
		cf[i]=a[i]-a[i-1];	
	} 
	for(int i=1;i<=n;i++)
	{
	    prv[i]=prv[i-1]+max(0ll,1-cf[i]);
	} 
	for(int i=n;i>=1;i--)
	{
		nxt[i]=nxt[i+1]+max(0ll,1+cf[i]);
	}
	for(int i=0;i<=n;i++)
	{
		ans=min(ans,max(prv[i],nxt[i+1]));
	}
	cout<<ans;
    return 0;	
} 

T3 决斗

题面

正在施工中...

T4 回文串问题

题面

正在施工中...