网络流——OI复健

鱼鱼在军训7天后(变炭烧鱼鱼了)彻底忘了如何打OI，但距 CSP-J/S2025 第一轮 还有 11 天，距 CSP-J/S2025 第二轮 还有 53 天，祂还有时间吗？

网络流

概念

贺自OI Wiki

其中\(f(u, v) = −f(v, u)\)也称为斜对称性。
在任意时刻，网络中所有节点以及剩余容量大于0的边构成的子图被称为残量网络

最大流

令 G=(V,E) 是一个有源汇点的网络，我们希望在 \(G\) 上指定合适的流 \(f\)，以最大化整个网络的流量 \(|f|\)（即 \(\sum_{x \in V} f(s, x) - \sum_{x \in V} f(x, s)\)），这一问题被称作最大流问题。通俗来讲，即求 \(s\) 到 \(t\) 的最大流量。
不会讲qwq
来看DALAO的博客（link1,link2）

例题

P3376 【模板】网络最大流

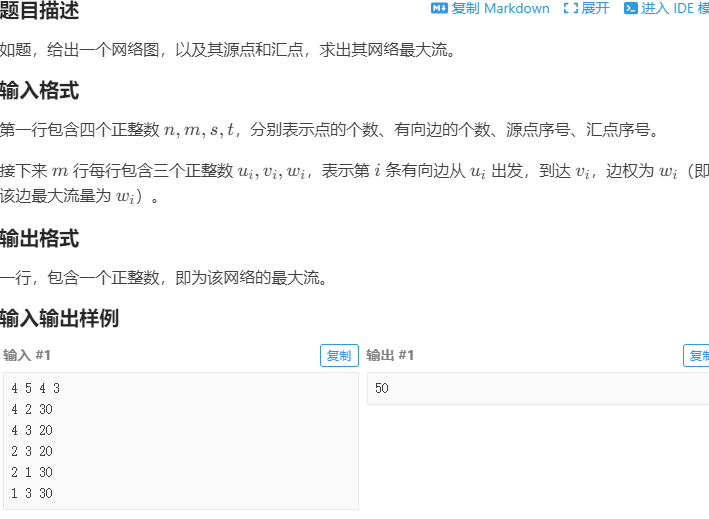
代码

#include<bits/stdc++.h>
using namespace std;
const int inf=INT_MAX;
int n,m,s,t;
int h[5010],to[10010],nxt[10010];
long long v[10010];
int now_cur[5010];//当前弧优化
long long dis[10010];
int tot=1;
void add(int x,int y,long long val)
{
    tot++;
	to[tot]=y;
	v[tot]=val;
	nxt[tot]=h[x];
	h[x]=tot;	
}
bool bfs()//在残量网络中构造分层图 
{
	memset(dis,0,sizeof(dis));
	queue <int> q;
	q.push(s);
	dis[s]=1;
	while(!q.empty())
	{
		int x=q.front();
		q.pop();
		for(int i=h[x];i;i=nxt[i])
		{
			int y=to[i];
			if(!dis[y]&&v[i])
			{
				dis[y]=dis[x]+1;
				q.push(y);
			}
		}
	}
	if(dis[t]==0)
	{
		return 0;
	}
	else
	{
		return 1;
	}
}
long long dfs(int x,long long sum)//sum是整条增广路对最大流的贡献
{
	if(x==t)
	{
		return sum;
	}
	long long res=0;
	/*
        对于一个节点x，当它在DFS中走到了第i条弧时，
	前i-1条弧到汇点的流一定已经被流满而没有可行的路线了
	因为我们每次向某条边的方向推流的时候, 肯定要么把推送量用完了, 要么是把这个方向的容量榨干了 
	那么当下一次再访问x节点时，前i-1条弧就没有任何意义了
	所以我们可以在每次枚举节点x所连的弧时，改变枚举的起点，
	这样就可以删除起点以前的所有弧，来达到优化剪枝的效果
        */ 
	for(int &i=now_cur[x];i&&sum;i=nxt[i])
	{
	    int y=to[i];
	    if(dis[x]+1==dis[y]&&v[i])
	    {
	    	long long k=dfs(y,min(sum,v[i]));//k是当前最小的剩余容量
	    	if(k==0)//剪枝，去掉增广完毕的点
	    	{
	    		dis[y]=0;
			}
			res+=k;//res表示经过该点的所有流量之和（相当于流出的总量）
			sum-=k;//sum表示经过该点的剩余流量 
			v[i]-=k;
			v[i^1]+=k;
			if(sum<=0)
			{
				return res;
			}
		}
	} 
	if(!res)
	{
		dis[x]=0;
	}
	return res;
}
long long dinic()
{
    long long ans=0;
	while(bfs())
	{
	    memcpy(now_cur,h,sizeof(now_cur));
	    ans+=dfs(s,inf);			
	}
	return ans;	
}
int main()
{
	cin>>n>>m>>s>>t;
	for(int i=1;i<=m;i++)
    {
	    int x,y;
		long long val;
	    cin>>x>>y>>val;
	    add(x,y,val);
		add(y,x,0); 
	} 
	cout<<dinic();
    return 0; 
} 

最小割

贺自OI Wiki

最大流最小割定理：

对于任意网络 \(G = (V, E)\)，其上的最大流 \(f\) 和最小割 \(\{S, T\}\) 总是满足$ |f| = ||S, T||$，即在任意网络中，可行流的最大流值等于最小割的容量。

经典问题

最小费用最大流

贺自OI Wiki

例题

P3381 【模板】最小费用最大流

代码

#include<bits/stdc++.h>
using namespace std;
long long mf,mc;
int s,t,m,n;
bool vis[5010];
int h[5010],to[100010],nxt[100010];
long long v[100010],vv[100010];
int tot=1;
int nc[5010];
const long long inf=0x3f3f3f3f3f3f3f3f; 
long long dis[5010];
void add(int x,int y,int val,int vval)
{
	tot++;
	to[tot]=y;
	nxt[tot]=h[x];
	v[tot]=val;
	vv[tot]=vval;
	h[x]=tot;
}
bool spfa()
{
	memset(dis,0x3f,sizeof(dis));
	memset(vis,0,sizeof(vis));
	queue <int> q;
	q.push(s);
	dis[s]=0;
	vis[s]=1;
	while(!q.empty())
	{
		int x=q.front();
		q.pop();
		vis[x]=0;
		for(int i=h[x];i;i=nxt[i])
		{
			int y=to[i];
			if(v[i]&&dis[x]+vv[i]<dis[y])
			{
				dis[y]=dis[x]+vv[i]; 
			    if(!vis[y])
			    {
			    	q.push(y);
					vis[y]=1; 
				}
			}
		}
	}
	if(dis[t]==inf)
	{
		return 0; 
	}
	else
	{
		return 1;
	}
}
int dfs(int x,long long sum)
{
	if(x==t)
	{
		return sum;
    }
    vis[x]=1;
    long long res=0;
    for(int &i=nc[x];i&&sum;i=nxt[i])
    {
    	int y=to[i];
    	if(!vis[y]&&v[i]&&dis[x]+vv[i]==dis[y])
    	{
    		int k=dfs(y,min(sum,v[i]));
    		if(!k)
    		{
    			dis[y]=inf;
			}
			v[i]-=k;
			v[i^1]+=k;
			res+=k;
			sum-=k;
			mc+=k*vv[i];
		}
	}
	vis[x]=0;
	return res; 
}
void dinic()
{
	while(spfa())
	{
		memcpy(nc,h,sizeof(nc));
		mf+=dfs(s,inf);
	}
} 
int main()
{
	cin>>n>>m>>s>>t;
	for(int i=1;i<=m;i++)
	{
		int x,y,a,b;
		cin>>x>>y>>a>>b;
		add(x,y,a,b);
		add(y,x,0,-b);
	}
    dinic();
    cout<<mf<<" "<<mc;
    return 0;
} 

最大权闭合子图

正在施工中...