笛卡尔树

笛卡尔树

定义

from:OI Wiki
笛卡尔树是一种二叉树，每一个节点由一个键值二元组 \((k,w)\) 构成。
要求 \(k\) 满足二叉搜索树的性质(即设\(root\)为根，其左子树内节点均小于\(root\)，其右子树内节点均大于\(root\))
而 \(w\) 满足堆的性质(分为大，小根堆，假设为大根堆，其\(root\)根节点大于其子节点，若为小根堆则根节点小于子节点)。
如果笛卡尔树的 \(k,w\) 键值确定，且 \(k\) 互不相同，\(w\) 也互不相同，那么这棵笛卡尔树的结构是唯一的。

如下图：

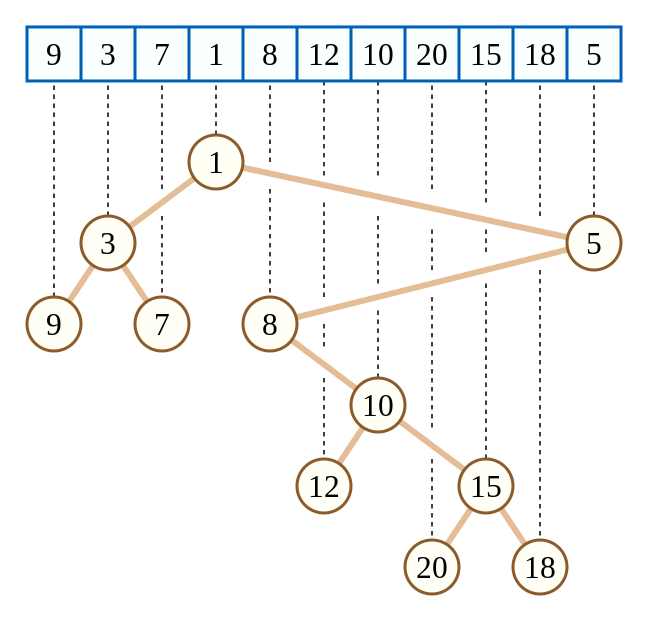
上面这棵笛卡尔树相当于把数组元素值当作键值 \(w\)，而把数组下标当作键值 \(k\)。
可以发现，这棵树的键值 \(k\) 满足二叉搜索树的性质，而键值 \(w\) 满足小根堆的性质。
同时根据二叉搜索树的性质，可以发现这种特殊的笛卡尔树满足一棵子树内的下标是一个连续区间。

笛卡尔树的构建方式

例题

洛谷 P5854 【模板】笛卡尔树

递归构建

以\(w\)满足小根堆性质为例：

1. 找到当前序列中\(w\)的最小值作为根节点。
2. 将序列划分成左子区间和右子区间。
3. 递归构建左右子树。

直接暴力时间复杂度为\(O(n^2)\),线段树优化之后为\(O(n \log n)\)

暴力代码

#include<bits/stdc++.h>
using namespace std;
struct jade
{
	int l,r;
}t[1000010];
int a[1000010];
int n;
int find_min(int l,int r)
{
	int minn=INT_MAX;
	int pos=0;
	for(int i=l;i<=r;i++)
	{
		if(a[i]<minn)
		{
			pos=i;
		    minn=a[i];	
		}
	}
	return pos;
}
void build(int root,int l,int r)
{
    if(l==r)
	{
		return ;
	}
	int pos_l=find_min(l,root-1);
	int pos_r=find_min(root+1,r);
	t[root].l=pos_l;
	t[root].r=pos_r;
	build(pos_l,l,root-1);
	build(pos_r,root+1,r);
}
int main()
{
	ios::sync_with_stdio(false);
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	int x=find_min(1,n);
	build(x,1,n);
	long long ans1=0,ans2=0;
	for(int i=1;i<=n;i++)
	{
		ans1^=(i*(t[i].l+1ll));
		ans2^=(i*(t[i].r+1ll));
	}
	cout<<ans1<<" "<<ans2;
	return 0;
}

线段树优化代码

#include<bits/stdc++.h>
using namespace std;
#define ls (ro<<1)
#define rs (ro<<1|1) 
int n;
struct jade
{
	int l,r;
}dkr[100010];
struct seek
{
	int l,r,minn,pos; 
}t[400010];
int a[100010];
void t_build(int ro,int l,int r)
{
	t[ro].l=l;
	t[ro].r=r;
	if(l==r)
	{
		t[ro].minn=a[l];
		t[ro].pos=l;
		return ;
	}
	int mid=(l+r)>>1;
	t_build(ls,l,mid);
	t_build(rs,mid+1,r);
	if(t[ls].minn<t[rs].minn)
	{
		t[ro].minn=t[ls].minn;
		t[ro].pos=t[ls].pos;
	}
	else
	{
		t[ro].minn=t[rs].minn;
		t[ro].pos=t[rs].pos;
	}
}
seek query(int ro,int l,int r)
{
	if(l<=t[ro].l&&r>=t[ro].r)
	{
		return t[ro];
	}
	int mid=(t[ro].l+t[ro].r)>>1;
	int minn=INT_MAX,pos=0;
	if(l<=mid)
	{
		seek ll=query(ls,l,r);
	    if(ll.minn<minn)
	    {
	    	minn=ll.minn;
	    	pos=ll.pos;
		}
	}
	if(r>mid)
	{
		seek rr=query(rs,l,r);
		if(rr.minn<minn)
		{
			minn=rr.minn;
			pos=rr.pos;
		}
	} 
	return {0,0,minn,pos};
}
void build(int ro,int l,int r)
{
	if(l==r)
	{
		return ;
	}
	int pos_l=query(1,l,ro-1).pos;
	int pos_r=query(1,ro+1,r).pos;
	dkr[ro].l=pos_l;
	dkr[ro].r=pos_r;
	build(pos_l,l,ro-1);
	build(pos_r,ro+1,r); 
}
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	t_build(1,1,n);
	int x=query(1,1,n).pos;
	build(x,1,n);
	long long ans1=0,ans2=0;
	for(int i=1;i<=n;i++)
	{
		ans1^=(i*(dkr[i].l+1ll));
		ans2^=(i*(dkr[i].r+1ll));
	}
	cout<<ans1<<" "<<ans2;
	return 0;
}

but!!不要直接贺这两段代码，它们的时复和空复都不足以通过本题，让我们来学习优秀的线性做法。

单调栈构建

以\(w\)满足小根堆性质为例:

1. 按照\(k\)的顺序依次插入节点。
2. 使用单调栈维护当前树的右链（从根节点到最右节点的路径）。
3. 每次插入时，调整栈顶元素以满足堆的性质,即从下往上比较右链节点与当前节点 \(x\) 的 \(w\)，如果找到了一个右链上的节点 \(y\) 满足 \(w_y<w_x\)，就把 \(x\) 接到 \(y\) 的右儿子上，而 \(y\) 原本的右子树就变成 \(x\) 的左子树。

图中红框部分就是我们始终维护的右链(即单调栈）：

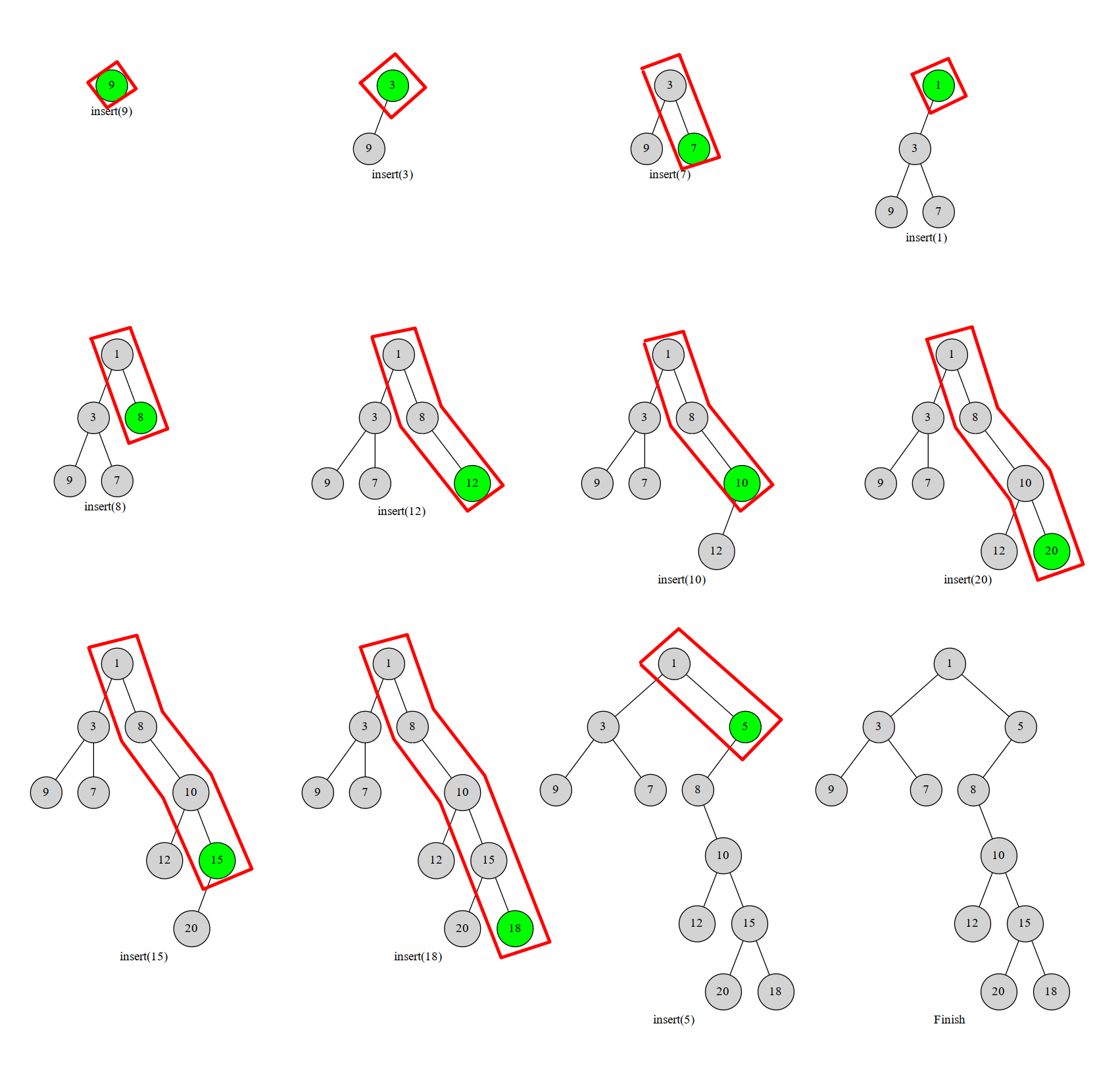
时间复杂度为\(O(n)\)

代码

#include<bits/stdc++.h>
using namespace std;
int a[10000010];
struct jade
{
	int l,r;
}dkr[10000010];
int stackk[10000010];
int top=1,n;
void build()
{
	stackk[1]=1;
	for(int i=2;i<=n;i++)
	{
		while(a[stackk[top]]>a[i])
		{
			top--;
		}
		 // 如果右链中没有一个比它大的元素，它就成了右链的链顶并且原来的链顶就是它的左儿子
		if(!top)
		{
			dkr[i].l=stackk[top+1];
		}
		// 把点 i 插入到某个点的下方，原本那个点的右儿子要变成 i 的左儿子，然后 i 来当右儿子
		else
		{
			dkr[i].l=dkr[stackk[top]].r;
			dkr[stackk[top]].r=i;
		}
		top++;
		stackk[top]=i;
	}
}
int main()
{
	ios::sync_with_stdio(false);
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	build();
	long long ans1=0,ans2=0;
	for(int i=1;i<=n;i++)
	{
		ans1^=(i*(dkr[i].l+1ll));
		ans2^=(i*(dkr[i].r+1ll));
	}
	cout<<ans1<<" "<<ans2;
	return 0;
}

记得开读入优化和long long

未完待续...