点分治（淀粉质）

点分治

好久之前学的啦！不补不行惹QAQ。

定义

点分治，是一种针对可带权树上简单路径统计问题的算法，适合处理大规模的树上路径信息问题。
本质上是优化暴力+容斥（即将一棵树拆分成许多子树进行处理）

前置知识

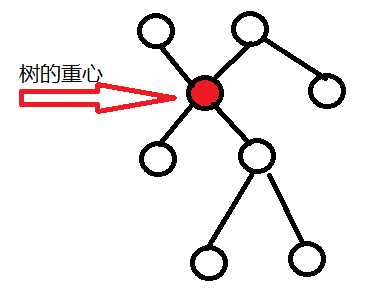
树的重心

定义

如果在树中选择某个节点并删除，这棵树将分为若干棵子树，统计子树节点数并记录最大值。取遍树上所有节点，使此最大值取到最小的节点被称为整个树的重心。

性质

• 树的重心如果不唯一，则至多有两个，且这两个重心相邻。
• 以树的重心为根时，所有子树的大小都不超过整棵树大小的一半。
• 树中所有点到某个点的距离和中，到重心的距离和是最小的；如果有两个重心，那么到它们的距离和一样。
• 把两棵树通过一条边相连得到一棵新的树，那么新的树的重心在连接原来两棵树的重心的路径上。
• 在一棵树上添加或删除一个叶子，那么它的重心最多只移动一条边的距离。

例子

实现方式/代码
求树的重心

用dfs求出sum，即以x为根的子树的大小，对于每个节点，它的\(sum_x=max(sum_y(y\in son_x),n-sum_x)\)。要与\(n-sum_x\)取max是因为把x删去后，x子树外会构成一个连通块

洛谷 U263740 树的重心（模板）

#include<bits/stdc++.h>
using namespace std;
int n;
int h[100010],to[200010],nxt[200010],tot;
int ans=100010;
bool vis[100010];
void add(int x,int y)
{
	tot++;
	to[tot]=y;
	nxt[tot]=h[x];
	h[x]=tot; 
}
int dfs(int x)
{
    int res=0,sum=1;
	vis[x]=1;
	for(int i=h[x];i;i=nxt[i])
	{
	    int y=to[i];
		if(!vis[y])
		{
		    int ysum=dfs(y);
			res=max(res,ysum);
			sum+=ysum;
		}	
	}
	res=max(res,n-sum);
	ans=min(ans,res);
	return sum;	
} 
int main()
{
    cin>>n;
    for(int i=1;i<n;i++)
    {
    	int x,y;
    	cin>>x>>y;
    	add(x,y);
    	add(y,x);
	}
	dfs(1);
	cout<<ans;
    return 0;	
} 

基本思想

在一棵有根树上，我们可以把路径分为两类；

• 经过树根的路径和不经过树根的路径。

点分治就是先计算合法的过根路径，再将根节点删去，递归分治若干子树，把不过根路径转化为子树内的过根路径。

但如果任意选取根节点来进行点分治算法，最坏情况下时间复杂度将退化为O(\(n^2\)),这是不可接受的。

那如果我们每次分治时以树的重心作为根，点分治算法的时间复杂度就平均为O(\(nlogn\)),是一个较优的复杂度。

考虑如何证明

根据树的重心的性质可知，以树的重心x为根的子树大小\(sum_x\)一定小于等于整棵树的节点数的一半，那么若每次选取树的重心作为根， 将根删除后，剩余连通块的大小皆小于等于\(n/2\)(n为整棵树的节点数）。即递归 \(logn\) 次就可以处理完整棵树。

实现方式/代码

洛谷 P2634 [国家集训队] 聪聪可可

#include<bits/stdc++.h>
using namespace std;
int n;
int h[100010],to[200010],nxt[200010],v[200010],tot;
int maxx[100010]; 
bool vis[100010];
int size[100010];
int dis[100010],t[5],now[5];
int S;//树的大小 
int root=0;//根初始为0 
int ans;
void add(int x,int y,int w)
{
	tot++;
	to[tot]=y;
	v[tot]=w;
	nxt[tot]=h[x];
	h[x]=tot; 
}
void getrt(int x,int fa)//找根（即树的重心 
{
    size[x]=1;//子数大小 
	maxx[x]=0;//比较数组 
	for(int i=h[x];i;i=nxt[i])//遍历子树 
	{
	    int y=to[i];//y为x的儿子 
		if(y==fa||vis[y])//避免重复遍历 
		{
		    continue;
		}	
		getrt(y,x);//递归 
		size[x]+=size[y];//统计子树大小 
		maxx[x]=max(maxx[x],size[y]);//比较，取最大值 
	}	
	maxx[x]=max(maxx[x],S-size[x]);//和非子树比较 
	if(maxx[x]<maxx[root])//若x比之前找到的答案更重 
	{
		root=x;//更新 
	}
} 
void getnum(int x,int fa)
{
	now[dis[x]%3]++;//统计答案 
	for(int i=h[x];i;i=nxt[i])
	{
		int y=to[i];
		if(vis[y]||fa==y)
		{
			continue;
		}
		dis[y]=dis[x]+v[i];//x->y 根到y的距离为根到x的距离+x到y的边权 
		getnum(y,x);//递归 
	}
}
void solve(int x)//对当前树统计答案 
{
	for(int i=h[x];i;i=nxt[i])//遍历 
	{
		int y=to[i];
		if(vis[y])//避免重复 
		{
		    continue;	
		} 
		memset(now,0,sizeof(now));//初始化 
		dis[y]=v[i];//x->y边权下放到儿子y 
		getnum(y,x);//求点到根的距离 
		ans+=t[0]*now[0]*2+t[1]*now[2]*2+t[2]*now[1]*2+now[0]*2;//记录答案 
		for(int j=0;j<3;j++)
		{
			t[j]+=now[j];//统计 
		}
	}
}
void Div(int x)//子树分治 
{
	vis[x]=1;//记录 
	solve(x);//以x为根对当前树统计答案 
	memset(t,0,sizeof(t));
	for(int i=h[x];i;i=nxt[i])//遍历儿子 
	{
		int y=to[i];
		if(vis[y])
		{
		    continue;
		} 
		S=size[y];//记录以x为根y的子树大小 
		root=0;//初始化 
		maxx[0]=999999999;
		getrt(y,0);//找y子树中的根 
		Div(root);//分治y子树 
	}
	return ;
}
int main()
{
    cin>>n;
    for(int i=1;i<n;i++)//输入 
    {
    	int x,y,w;
    	cin>>x>>y>>w;
    	add(x,y,w);//存图 
    	add(y,x,w);
	}
	maxx[root]=S=n;//0为根代表整棵树 
	getrt(1,0);//从1开始遍历求根 
	Div(root);//以root为根分治各个子树 
	int a=ans+n;//题目要求 
	int b=n*n;
	int c=__gcd(a,b);
	cout<<a/c<<"/"<<b/c;
    return 0;//by:jade_seek 
}
 

动态点分治

没学先鸽一鸽qwq

未完待续...