质数中的质数 2025.8.14 模拟赛

QAQ讨厌的T2挂我80分啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊

遂写一篇题解记录一下（m)

题目

样例

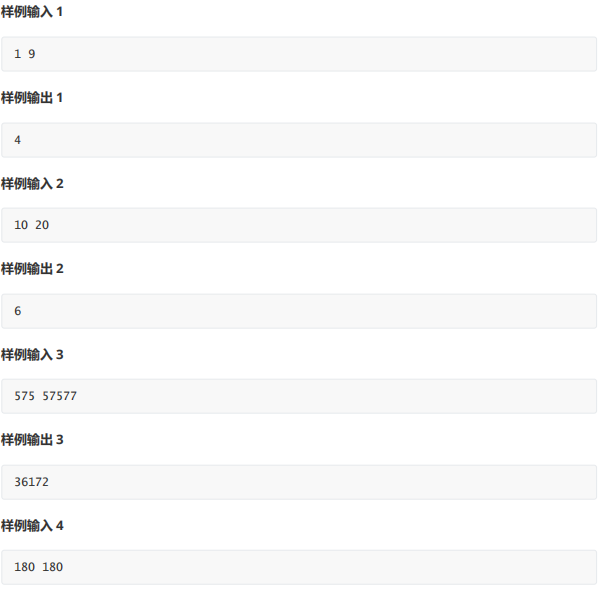
部分分80分

开题！
好！

“质数”“质因子”

欧拉筛直接薄杀了！（在筛质数的时一同将质因子个数记录下来）

• 因为欧拉筛的特性，一个合数只会被筛一次（两个数其中至少有一个质数且这两个数都被判断过）
• 开一个 sum 数组，对于 sum[i] 来说，其记录的为 i 这个数的质因子个数
• sum[i] 可由其筛它的两个数 prime[j] (第j个质数）和 k (合数）推得
• 即 sum[i]=sum[k]+1(因为质数 prime[j] 只有一个质因子即它本身)
• 判断质因子个数是否为质数也可以用 isp[质因子个数] 直接判断！

线性的时间复杂度已经很优了（才怪）
but..1e9的数据范围把我可爱的欧拉筛薄杀了QAQ
数组开不下时复也撞不过去
只能过1e7获得80分

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int prime[10000003];
bool isp[10000003];
short sum[10000003];
int tot=0;
int l,r;
void shai(int x)
{
	isp[0]=1;
	isp[1]=1;
	for(int i=2;i<=x;i++)
	{
		if(isp[i]==0)
		{
			tot++;
			prime[tot]=i;
			sum[i]=1;
		}
		for(int j=1;j<=tot&&prime[j]*i<=x;j++)
		{
			isp[prime[j]*i]=1;
			sum[prime[j]*i]=sum[i]+1;
		    if(i%prime[j]==0)
			{
				break;
			}
		}
	}
}
int main()
{
	freopen("prime.in","r",stdin);
	freopen("prime.out","w",stdout);
    cin>>l>>r;
    int ans=0;
    shai(r);
    for(int i=l;i<=r;i++)
    {
    	if(isp[sum[i]]==0)
    	{
    		ans++;
		}
	}
    cout<<ans; 
	return 0;
}

我就只能止步于此了吗？？

错！看我的(爆零)大法 hia hia hia hia hia~~

经过我一系列诡谲的计算
发现这个思路可以过1e8(万一后面两个点有1e8呢OvO)
但由于我太蒟蒻忘了计算空间复杂度(我是唐必!我要当车!!发动必死技!!!螳臂当车!!!!)
交上去直接全部RE获得了0分的好成绩！（为什么不是MLE我也不知道！）

我就只能止步于此了吗？？

对！让我（赛后）来打正解

我们注意到一个数的质因子大多很小
在1e5左右（大概也许可能）
所以可以用80分的方法先处理到1e5
剩余的数进行分解质因数
时间复杂度在1e5~9e6之间
可以通过此题
（别忘了计算空间复杂度为 3e5 QAQ）

代码

#include<bits/stdc++.h>
using namespace std;
int prime[100010];//存质数 
bool isp[100010];//判断质数 
short sum[100010];//质因数个数 
int tot=0;//质数个数 
int l,r; 
void shai(int x)//欧拉筛 
{
	isp[0]=1;//0,1不是质数 
	isp[1]=1;
	for(int i=2;i<=x;i++)
	{
		if(isp[i]==0)//i为质数 
		{
			tot++;//质数个数加一 
			prime[tot]=i;//记录 
	        sum[i]=1;//i为质数，所以质因数个数为1 
		}
		for(int j=1;j<=tot&&prime[j]*i<=x;j++)//进行筛 
		{
			isp[prime[j]*i]=1;//prime[j]*i为合数 
			sum[prime[j]*i]=sum[i]+1;//prime[j]*i的质因数个数为i的质因数个数加一（可以自己脑一下 
		    if(i%prime[j]==0)
			{
				break;
			}
		}
	}
}
int split(int x)//分解质因数 
{
	int cnt=0;//x的质因数个数 
	for(int i=1;i<=tot&&prime[i]*prime[i]<=x;i++)//分解质因数 
	{
		while(x%prime[i]==0)//prime[i]为x的因数 
		{
			x/=prime[i];
			cnt++;//个数加一 
		}
	}
	if(x>1)//剩余或x为质数 
	{
		cnt++;
	}
	return cnt; 
}
int main()
{
	freopen("prime.in","r",stdin);
	freopen("prime.out","w",stdout);
    cin>>l>>r;
    int ans=0;//质中质的个数 
    shai(1e5+5);//预处理到1e5 
    for(int i=l;i<=r;i++)
    {
    	if(i<=1e5)//预处理过O(1)求答案 
    	{
    		if(isp[sum[i]]==0)//i的质因数个数为质数 即i为质数中的质数 
    	    {
    	    	ans++;
		    }
		}
		else
		{
			if(isp[split(i)]==0)//分解i求质因数个数并进行判断 
			{
				ans++;
			}
		}
    }
    cout<<ans; //输出 
	return 0;//by: jade_seek 
}

\({\cal {The }}\) \({\cal {end. }}\)