后缀数组 子串处理

定义

• 两个字符串的大小关系为字典序大小

字典序大小简单来说就是从前往后比较，第一个不相同的位置得到的比较结果就是字典序大小

• （比如 \(abde\) < \(abea\)），空字符比所有字符小（即长度较短的字符串后面用空字符补齐，比如 \(abc\)<\(abcd\)。

一个字符串的所有子串就是这个字符串的所有后缀的所有前缀。

• 解决子串问题要先对一个字符串的所有后缀进行排序

后缀数组，实际上就是表示排完序后的后缀顺序。

• 更具体地，我们要求出数组 \(sa_i\)，表示第 i 大的前缀是从第 \(sa_i\) 个字符开始的后缀。为了方便，我们同时维护一个数组 \(rk_i\) 表示后缀 i 的排名。

倍增排序方式

• 首先将所有长度为 1 的字符串进行排序
• 然后对所有长度为 2 的字符串进行排序
• 然后再所有长度为 4 的字符串进行排序。

如果知道所有长度为 w 的字符串的排名，那么长度为 2w 的字符串就可以表示成一个二元组，表示前 w 个字符组成的字符串排名与后 w 个字符组成的字符串排名。

如图

排序过程

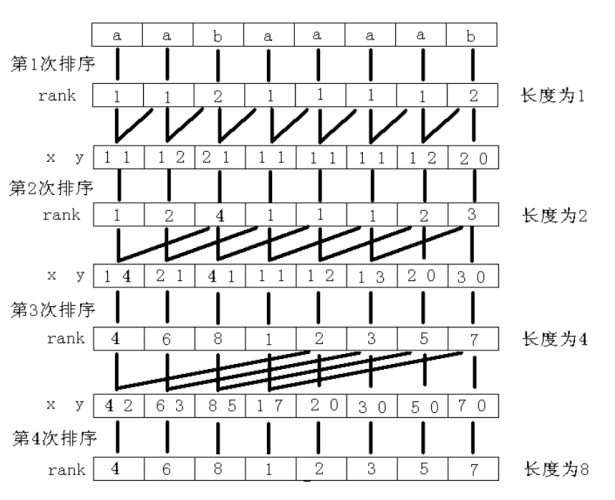
基数排序

• 我们要对二元组进行排序，所以可以直接进行基数排序。

基数排序，就是将一些数划分成一个 w 元数(w 元数的比较规则是从高位到低位比较，与字典序相同，这里划分就是将其写成某个进制的表示然后按位拆开)
例子说明
如图

• 然后从低位到高位依次进行计数排序。

计数排序就是我们记录每个元素的出现次数,后进行前缀和

• 这样每个位置 \(x\) 相当于存的是有多少数\(≤x\)，这便是 \(x\) 的排名。

我们每计算一个数的排名后需要将这个数删去,而且为了保证相同值的相对位置不变，我们需要从后往前去计算排名。

正确性证明

考虑你对最低位排序之后，再对高位排序，低位排序的顺序是不变的，这样高位相同的低位仍然是有序的，这样整个数就是有序的。复杂度就是 \(O((n + w)logw\) \(n)\)。

ps:排完序后我们需要计算新的排名。注意我们这时候得到的排名必须是经过去重的。

常数优化

• 我们实际上不需要再对第二关键字进行排序，因为当前我们已经有有序的数组了。于是我们可以利用这已经有序的数组直接将按照第二关键字排序的数组推出来，这样只需要进行一次计数排序了。
• 并不需要真的完全排序完，只要当不同的排名已经有 \(n\) 个时就可以结束了。

代码

int n,m;//n为后缀个数，m为桶的个数 
string s;
int x[2000010],y[2000010],c[2000010],sa[2000010],rk[2000010],height[2000010]; 
//桶数组x[i],辅助数组y[i],计数数组c[i] 
void get_sa()
{
	//按第一个字母排序 
	for(int i=1;i<=n;i++)
	{
		x[i]=s[i-1];
		c[x[i]]++;
	}
	for(int i=1;i<=m;i++)
	{
		c[i]+=c[i-1];
	}
	for(int i=n;i>=1;i--)
	{
		sa[c[x[i]]]=i;
		c[x[i]]--;
	}
	for(int k=1;k<=n;k<<=1)//logn次排序 
	{
		//按第一关键字排序 
		memset(c,0,sizeof(c));
		for(int i=1;i<=n;i++)
		{
			y[i]=sa[i];
		}
		for(int i=1;i<=n;i++)
		{
			c[x[y[i]+k]]++;
		}
		for(int i=1;i<=m;i++)
		{
			c[i]+=c[i-1];
		}
		for(int i=n;i>=1;i--)
		{
			sa[c[x[y[i]+k]]]=y[i];
			c[x[y[i]+k]]--;
		}
		//按第二关键字排序
		memset(c,0,sizeof(c));
		for(int i=1;i<=n;i++)
		{
			y[i]=sa[i];
		}
		for(int i=1;i<=n;i++)
		{
			c[x[y[i]]]++;
		}
		for(int i=1;i<=m;i++)
		{
			c[i]+=c[i-1];
		}
		for(int i=n;i>=1;i--)
		{
			sa[c[x[y[i]]]]=y[i];
			c[x[y[i]]]--;
		}
		//把后缀放入桶数组中 
		for(int i=1;i<=n;i++)
		{
			y[i]=x[i];
		}
		m=0;
		for(int i=1;i<=n;i++)
		{
			if(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])
			{
				x[sa[i]]=m;
			}
			else
			{
				m++;
				x[sa[i]]=m;
			}
			if(m==n)//排好 
			{
				break;
			}
		}
	}
}

朴素用法
查找子串出现位置/次数

由于后缀已经排序好了，我们可以直接在后缀数组上查找。

后缀排序重要的性质就是前缀相同的字符串出现在连续一段内，所以我们查询的字符串为开头的后缀也出现在连续一段内。

• 对于后缀数组中两个后缀 \(S[i, n]\), \(S[j, n]\)，他们中间的所有字符串的开头一定也是\(lcp(i, j)\)
  那么，如果我们求出每相邻两个后缀之间的 lcp，
  那么我们只需要区间取 min，即可得到两个后缀之间的 lcp。
• 我们设\(height_i\) = \(lcp(sa_i ,sa_i−1)\)，那么 \(lcp(i, j)\)=\(min_{i<k≤j}\) \(height_k\)。

这个可以简单使用 ST 表做到单次 O(1) 查询。

求 height 数组

引理
对于两个位置上相邻的前缀，他们的 \(height\) 最多差1,具体来说就是

\[height[rk_i] ≥ height[rk_i−1] − 1 \]

得知这点之后，我们就可以按照\(height[i]\)的性质，对字符串从前往后生成\(height\)数组的值，每次求出\(height[i-1]\),下一次求\(height[i]\)时，可以从\(height[i-1]-1\)位开始匹配\(lcp\)。
时间复杂度为 \(O(n)\) 。
代码

void get_height()
{
	for(int i=1;i<=n;i++)
	{
		rk[sa[i]]=i;
	}
	int k=0;
	for(int i=1;i<=n;i++)//枚举后缀i 
	{
		if(rk[i]==1)//第一名的height为0 
		{
			continue;
		}
		if(k)//上一个后缀的height值减一 
		{
		    k--; 
		} 
		int j=sa[rk[i]-1];//j为后缀i的前邻后缀 
		while(i+k<=n&&j+k<=n&&s[i+k-1]==s[j+k-1])
		{
			k++;
		}
		height[rk[i]]=k;
	}
}

应用

比较两个子串的大小关系
由字典序定义可以得知，两个字符串应该是前面会有共同的一段，然后有一个位置发生改变，此时可以比较大小。
前面共同的一段就是 \(lcp\)，知道它之后再比较一个字符就能得出两个子串的大小关系了，于是就能 \(O(1)\) 比较了。
不同子串的数目
一个字符串的子串就是其所有后缀的所有前缀。为了去重，我们只需要知道每个后缀的不同前缀与上一个后缀的不同前缀差多少，这个其实就是这两个后缀之间的 \(lcp\)。那么，我们只需要将这些子串减去即可，也就是说本质不同子串个数有：

\[\frac{n(n+1)}{2}-\sum_{i=1}^N height_i \]

未完待续...