manacher 马拉车算法 寻找最长回文子串

例题

洛谷 P3805 【模板】manacher

回文串的定义

回文串是字符串中常见的一种，一个字符串是回文串代表这个字符串从前往后和从后往前读是相等的，形式化定义就是一个长为 \(n\) 字符串, \(S\) 是回文的当且仅当对于任意 i，有 \(S_i = S_n−i+1\)

回文串的性质：一个回文串左右同时加一个字符，得到的仍然是回文串。

启示
可以从一个中心开始向左右拓展,添加字符，能拓展就拓展，拓展不了那么说明以这个为中心的更长的串一定也不是回文串。于是对于每一个中心点 \(c\)，我们都存在一个最长回文半径 \(r\)。

如图

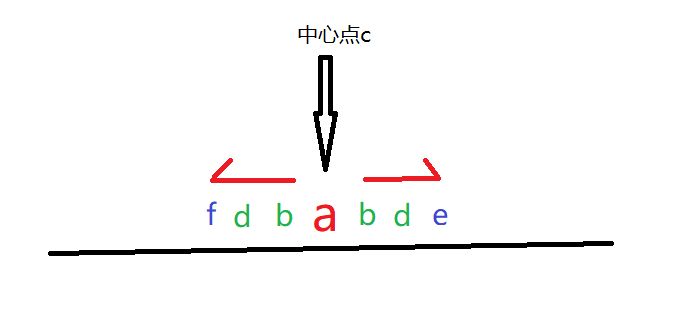
中心点为a, 最长回文半径是3，绿色为可扩展字符，蓝色为不可扩展字符

奇偶串的处理

有些串的中心在两个字符中间，而有些串的中心正好是一个字符。为了方便起见，我们可以先在每个字符中间加入一个分割符，这样原串中所有的回文串就都以一个字符为中心了。
大概就是，假如我们现在有一个字符串 \(S = racecar\)，我们就可以将它变成一个字符串 \(S = |r|a|c|e|c|a|r|\)。

答案统计

接下来只考虑以某个位置为中心的最长回文串半径 \(r_i\)（即最长回文串为 \(S[i − r_i + 1, i + r_i − 1]\)），原串的最长回文串长度就等于\(r_i − 1\)（因为中间加了分隔符），以该字符为中心的回文串有\(\llcorner r_i/2\lrcorner\) 。

算法原理

如果一个长回文串中有一个子回文串，那么这个子回文串翻转过后的位置一定也是一个回文串。
如图

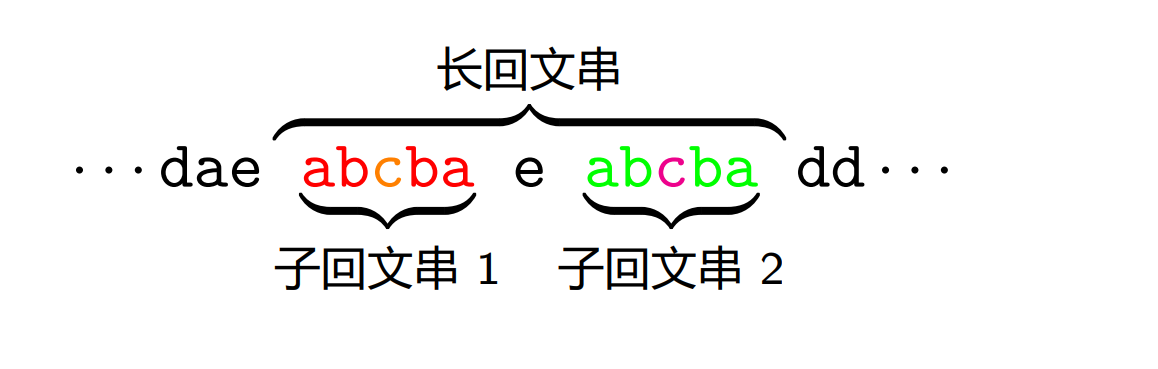
记录当前最长的一个回文串(右端点最靠右），这样当我们寻找以当前字符 \(c\) 为中心的最长回文串时，我们可以直接用 \(c'\) 为中心的最长子回文串的半径为初始值（ \(c'\) 为当前字符 \(c\) 在最长回文串的对称点），然后在这基础上再进行拓展。需要注意的是，以 \(c\) 为中心的最长回文串实际上是 \(aeabcbaea\)，是比长回文串更长的，所以我们需要把它缩减到长回文串内部再进行拓展，所以需要取一个 min。

如果当前中心已经不在最长回文串内了，那就直接从当前点 \(c\) (r为1) 开始拓展。

时间复杂度：\(O(n)\)

代码

#include<bits/stdc++.h>
using namespace std;
char t[22000010];//加了分隔符的串 
int l[22000010];//以i为中心点的回文串的半径 
int main()
{
    string s;
	cin>>s;
	t[1]='|';//分隔符，避免区分奇偶串 
	int n=s.size();
	for(int i=1;i<=n;i++)
	{
		t[2*i]=s[i-1];
		t[2*i+1]='|';
    }
    n=2*n+1;
    int c=0,r=-1;//c:最靠右的回文串的中心点，r:遍历过的串的最右右端点 
    int ans=0;//答案即最长回文串的长度 
    for(int i=1;i<=n;i++)//枚举中心点 
    {
    	if(i<=r)//中心点在之前最右回文串的右端点之前，即可以通过之前的状态进行转移 
    	{
    		l[i]=min(l[2*c-i],r-i);//以i为中心点的半径是i关于c的对称点为中心点的回文串的半径和i与r距离的较小值 
        }
		else
		{
			l[i]=1;//扩展初始值为1 
		}
		while(i-l[i]>=1&&i+l[i]<=n&&t[i+l[i]]==t[i-l[i]])//子串被包含且构成回文，利用的是回文串的性质 
		{
			l[i]++;//半径加一 
		}
		if(i+l[i]-1>r)//中心点加半径大于遍历过的串的最右右端点
		{
		    c=i;//更新中心点 
		    r=i+l[i]-1;//更新最右右端点 
		} 
		ans=max(ans,l[i]-1);//更新答案 
	}
	cout<<ans;
	return 0;
}

\({\cal {The }}\) \({\cal {end. }}\)