分块&莫队
分块
分块是一种思想,通过对原数据的适当划分,并在划分后的每一个块上预处理部分信息,从而较一般的暴力算法取得更优的时间复杂度。
优点: 分块是一种很灵活的思想,实现起来也比较简单,相较于树状数组和线段树,分块的优点是通用性更好,可以维护很多树状数组和线段树无法维护的信息。
缺点: 一般情况下时间复杂度比线段树和树状数组要高
时间复杂度:
分块的时间复杂度主要取决于分块的块长,一般可以通过均值不等式求出某个问题下的最优块长,以及相应的时间复杂度
块的大小为b,当b=\(\sqrt{n}\) 时,单次操作的时间复杂度最优,为O(\(\sqrt{n}\)) ,总时间复杂度为O(m*\(\sqrt{n}\))
例题

分析
我们将序列按每s个元素一块进行分块,并记录每块的区间和 bi。
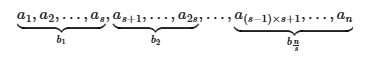
最后一个块可能是不完整的(因为n很可能不是s的倍数),但是这对于我们的讨论来说并没有太大影响。
首先看查询操作:
- 若 l 和 r 在同一个块内,直接暴力求和即可,因为块长为 s,因此最坏复杂度为 O(s)。
- 若 l 和 r 不在同一个块内,则答案由三部分组成:以 l 开头的不完整块,中间几个完整块,以 r 结尾的不完整块。对于不完整的块,仍然采用上面暴力计算的方法,对于完整块,则直接利用已经求出的 bi 求和即可。这种情况下,最坏复杂度为 O(n/s+s)。
接下来是修改操作:
- 若 l 和 r 在同一个块内,直接暴力修改即可,因为块长为 s,因此最坏复杂度为 O(s)。
- 若 l 和 r 不在同一个块内,则需要修改三部分:以 l 开头的不完整块,中间几个完整块,以 r 结尾的不完整块。对于不完整的块,仍然是暴力修改每个元素的值(别忘了更新区间和 bi),对于完整块,则直接修改 bi 即可。这种情况下,最坏复杂度和仍然为O(n/s+s)。
利用均值不等式可知,当n/s=s,即s=\(√n\) 时,单次操作的时间复杂度最优,为 O(\(√n\)).
代码
#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[100010];
int L[400],R[400],pos[100010],cnt;
//L[i]和R[i]表示第i段的左右端点,pos[i]表示a序列中的第i个位置的数位于第几段
//cnt表示分成的段数
long long sum[400],add[400];
// sum表示块内元素总和,add数组记录每个块的整体赋值情况,类似于 lazy_tag
void init()
{
cnt=sqrt(n);//即上述题解中的s, sqrt的时候时间复杂度最优
for(int i=1;i<=cnt;i++)
{
L[i]=(i-1)*cnt+1;
R[i]=i*cnt;
}
if(R[cnt]<n)//分出sqrt(n)块后,还有剩余的部分,单独再分一块
{
cnt++;
L[cnt]=R[cnt-1]+1;
R[cnt]=n;
}
//预处理pos和sum
for(int i=1;i<=cnt;i++)
{
for(int j=L[i];j<=R[i];j++)
{
pos[j]=i;
sum[i]+=a[j];
}
}
}
long long Q(int l,int r)
{
long long ans=0;
int p=pos[l];
int q=pos[r];
if(p==q)//l~r处于同一分块中
{
for(int i=l;i<=r;i++)
{
ans+=a[i];
}
ans+=(r-l+1)*add[p];
}
else
{
//先处理整块数据
for(int i=p+1;i<q;i++)
{
ans+=sum[i]+add[i]*(R[i]-L[i]+1);
}
//处理最左边块
for(int i=l;i<=R[p];i++)
{
ans+=a[i];
}
ans+=(R[p]-l+1)*add[p];
//处理最右边块
for(int i=L[q];i<=r;i++)
{
ans+=a[i];
}
ans+=(r-L[q]+1)*add[q];
}
return ans;
}
void U(int l,int r,int v)
{
int p=pos[l];
int q=pos[r];
if(p==q)//l~r处于同一分块中
{
for(int i=l;i<=r;i++)
{
a[i]+=v;
}
sum[p]+=v*(r-l+1);
}
else
{
//先处理整块数据
for(int i=p+1;i<q;i++)
{
add[i]+=v;
}
//处理最左边块
for(int i=l;i<=R[p];i++)
{
a[i]+=v;
}
sum[p]+=v*(R[p]-l+1);
//处理最右边块
for(int i=L[q];i<=r;i++)
{
a[i]+=v;
}
sum[q]+=v*(r-L[q]+1);
}
}
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
init();
while(m--)
{
string s;
cin>>s;
if(s[0]=='Q')
{
int l,r;
cin>>l>>r;
long long ans=Q(l,r);
cout<<ans<<endl;
}
else
{
int l,r,v;
cin>>l>>r>>v;
U(l,r,v);
}
}
return 0;
}
莫队
莫队算法是由莫涛提出的算法。
莫队算法可以解决一类离线区间询问问题,适用性极为广泛。同时将其加以扩展,便能轻松处理树上路径询问以及支持修改操作。
普通莫队算法
形式
假设 n=m,那么对于序列上的区间询问问题,如果从 [l,r] 的答案能够 O(1) 扩展到 [l-1,r],[l+1,r],[l,r+1],[l,r-1](即与 [l,r] 相邻的区间)的答案,那么可以在 O(mn) 的复杂度内求出所有询问的答案。
例题

暴力枚举代码
#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[50010];
int l=1,r;
int cnt[1000010];
int ans;
void add(int x)
{
if(cnt[x]==0)
{
ans++;
}
cnt[x]++;
}
void del(int x)
{
cnt[x]--;
if(cnt[x]==0)
{
ans--;
}
}
int main()
{
int x,y;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
cin>>m;
while(m--)
{
cin>>x>>y;
while(x<l)
{
l--;
add(a[l]);
}
while(y>r)
{
r++;
add(a[r]);
}
while(x>l)
{
del(a[l]);
l++;
}
while(y<r)
{
del(a[r]);
r--;
}
cout<<ans<<endl;
}
return 0;
}
优化:分块排序版
解释
离线后排序,顺序处理每个询问,暴力从上一个区间的答案转移到下一个区间答案(一步一步移动即可)。
排序方法
对于区间 [l,r], 以 l 所在块的编号为第一关键字,r 为第二关键字从小到大排序。
时间复杂度
O(n\(\sqrt{n}\))。
证明

分块排序代码
#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[50010];
int l=1,r=0;
int col[1000010],num=0,ans[200010];
int L[50010],R[50010],pos[50010],cnt=0;
struct jade
{
int x,y,id;
}q[200010];
bool cmp(jade nod1,jade nod2)
{
int p=pos[nod1.x],q=pos[nod2.x];
if(p==q)
{
return nod1.y<nod2.y;
}
return p<q;
}
void init()
{
int B=n/sqrt(m);
cnt=n/B;
for(int i=1;i<=cnt;i++)
{
L[i]=n/cnt*(i-1)+1;
R[i]=n/cnt*i;
}
if(R[cnt]<n)
{
cnt++;
L[cnt]=R[cnt-1]+1;
R[cnt]=n;
}
for(int i=1;i<=cnt;i++)
{
for(int j=L[i];j<=R[i];j++)
{
pos[j]=i;
}
}
}
void add(int x)
{
if(col[x]==0)
{
num++;
}
col[x]++;
}
void del(int x)
{
col[x]--;
if(col[x]==0)
{
num--;
}
}
int main()
{
int x,y;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
init();
cin>>m;
for(int i=1;i<=m;i++)
{
cin>>x>>y;
q[i]={x,y,i};
}
sort(q+1,q+1+m,cmp);
for(int i=1;i<=m;i++)
{
x=q[i].x;
y=q[i].y;
while(x<l)
{
l--;
add(a[l]);
}
while(y>r)
{
r++;
add(a[r]);
}
while(x>l)
{
del(a[l]);
l++;
}
while(y<r)
{
del(a[r]);
r--;
}
ans[q[i].id]=num;
}
for(int i=1;i<=m;i++)
{
cout<<ans[i]<<endl;
}
}
优化:奇偶排序版
解释:奇偶化排序即对于属于奇数块的询问,r 按从小到大排序
对于属于偶数块的排序,r 从大到小排序
这样我们的 r 指针在处理完这个奇数块的问题后,将在返回的途中处理偶数块的问题,再向 n 移动处理下一个奇数块的问题
优化了 r 指针的移动次数,一般情况下,这种优化能让程序快 30% 左右。
奇偶排序代码
#include <bits/stdc++.h>
using namespace std;
int n,m;
int a[50010];
//莫队信息
int l=1,r=0,col[1000010],num=0,ans[200010];
//分块信息
int L[50010],R[50010],pos[50010],cnt;
struct node
{
int x, y, id;
}q[200010];
//奇偶排序
//左端点按所在块,由小到大排序
//奇数块时右端点由小到大,偶数块右端点由大到小
//奇偶排序可以做到上一块r由1~n,该块r由n~1
bool cmp(node &nod1, node &nod2)
{
int p=pos[nod1.x];
int q=pos[nod2.x];
if(p!=q)
{
return p < q;
}
if(p&1==1)
{
return nod1.y<nod2.y;
}
else
{
return nod1.y>nod2.y;
}
}
void init()
{
//当块的大小取n/sqrt(m)时,时间复杂度可以达到最优
int B=n/sqrt(m);
cnt=n/B;
for(int i=1;i<=cnt;i++)
{
L[i]=B*(i-1)+1;
R[i]=B*i;
}
if(R[cnt]<n)
{
cnt++;
L[cnt]=R[cnt-1]+1;
R[cnt]=n;
}
for(int i=1;i<=cnt;i++)
{
for(int j=L[i];j<=R[i];j++)
{
pos[j]=i;
}
}
}
void add(int x)
{
if(col[x]==0)
{
num++;
}
col[x]++;
}
void del(int x)
{
col[x]--;
if(col[x]==0)
{
num--;
}
}
int main()
{
int x,y;
cin>>n;
for(int i=1; i<=n; i++)
{
cin>>a[i];
}
//分块
cin>>m;
init();
for(int i=1;i<=m;i++)
{
cin>>x>>y;
q[i]={x,y,i};
}
sort(q+1,q+1+m,cmp);
for(int i=1;i<=m;i++)
{
x=q[i].x;
y=q[i].y;
while(x<l)
{
l--;
add(a[l]);
}
while(y>r)
{
r++;
add(a[r]);
}
while(x>l)
{
del(a[l]);
l++;
}
while(y<r)
{
del(a[r]);
r--;
}
ans[q[i].id]=num;
}
for(int i=1;i<=m;i++)
{
cout<<ans[i]<<endl;
}
}
带修莫队
带修莫队是一种支持单点修改的莫队算法。
普通莫队是不能带修改的,我们可以强行让他可以修改,就像dp一样,可以强行加上一维时间维,表示这次操作的时间
即把询问\([l,r]\)变成\([l,r,\text{time}]\)。
那么我们的坐标也可以在时间维上移动,即 $[l,r,\text{time}] $多了一维可以移动的方向,可以变成:
这样的转移也是 O(1) 的,但是我们排序又多了一个关键字
排序的方式是以 \(n^{2/3}\) 为一块,分成了 \(n^{1/3}\) 块,第一关键字是左端点所在块,第二关键字是右端点所在块,第三关键字是时间。
时间复杂度: O(\(n^{5/3}\))
排序的方式是以 \(n^{2/3}\) 为一块,分成了 \(n^{1/3}\) 块
例题

代码
#include<bits/stdc++.h>
using namespace std;
int a[150010];
int l=1,r=0,t=0;
int col[1000010],num=0;
int ans[150010];
int L[500],R[500],pos[150010],cnt=0;
int n,m;
struct jade
{
int id,l,r,t;//t表示该询问位于第几次修改
}q[150010];
struct seek//存储修改信息
{
int x,c;
}rp[150010];
bool cmp(jade &nod1,jade &nod2)
{
//先按左端点所在块升序
//左端点块相同按右端点所在块升序
//左右端点块相同,按t升序
int p=pos[nod1.l];
int q=pos[nod2.l];
if(p!=q)
{
return p<q;
}
p=pos[nod1.r];
q=pos[nod2.r];
if(p!=q)
{
return p<q;
}
return nod1.t<nod2.t;
}
//分块
void init()
{
int B=pow(n,0.666);
cnt=n/B;
for(int i=1;i<=cnt;i++)
{
L[i]=(i-1)*B+1;
R[i]=i*B;
}
if(R[cnt]<n)
{
cnt++;
L[cnt]=R[cnt-1]+1;
R[cnt]=n;
}
for(int i=1;i<=cnt;i++)
{
for(int j=L[i];j<=R[i];j++)
{
pos[j]=i;
}
}
}
void add(int x)
{
if(col[x]==0)
{
num++;
}
col[x]++;
}
void del(int x)
{
col[x]--;
if(col[x]==0)
{
num--;
}
}
int main()
{
string s;
int x,y;
int mq=0,mr=0;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
for(int i=1;i<=m;i++)
{
cin>>s>>x>>y;
if(s[0]=='Q')//单独记录查询的信息
{
mq++;
q[mq]={mq,x,y,mr};
}
else//单独记录修改的信息
{
mr++;
rp[mr]={x,y};
}
}
init();
sort(q+1,q+1+mq,cmp);
for(int i=1;i<=mq;i++)
{
//朴素莫队操作
while(q[i].l<l)
{
l--;
add(a[l]);
}
while(q[i].l>l)
{
del(a[l]);
l++;
}
while(q[i].r<r)
{
del(a[r]);
r--;
}
while(q[i].r>r)
{
r++;
add(a[r]);
}
//在完成朴素莫队更新后,还要判断修改时间,将修改时间更新到正确位置
while(q[i].t<t)
{
if(rp[t].x>=l&&rp[t].x<=r)//修改的数据位于[l,r]之间,则需要更新,否则不需要更新
{
del(a[rp[t].x]);
add(rp[t].c);
}
swap(a[rp[t].x],rp[t].c);//注意这里是交换值,不是直接更改a数组,因为后面还要回滚
t--;
}
while(q[i].t>t)
{
t++;
if(rp[t].x>=l&&rp[t].x<=r)
{
del(a[rp[t].x]);
add(rp[t].c);
}
swap(a[rp[t].x],rp[t].c);
}
ans[q[i].id]=num;
}
for(int i=1;i<=mq;i++)
{
cout<<ans[i]<<endl;
}
return 0;
}
回滚莫队
引入:
- 有些题目在区间转移时,可能会出现增加或者删除无法实现的问题。在只有增加不可实现或者只有删除不可实现的时候,就可以使用回滚莫队在
的时间内解决问题。 - 回滚莫队分为只使用增加操作的回滚莫队和只使用删除操作的回滚莫队。
复杂度证明
假设回滚莫队的分块大小是 b:
对于左、右端点在同一个块内的询问,可以在 O(b) 时间内计算;
对于其他询问,考虑左端点在相同块内的询问,它们的右端点单调递增,移动右端点的时间复杂度是 O(n),而左端点单次询问的移动不超过 b,
因为有 \(\frac{n}{b}\) 个块,所以总复杂度是 O(mb+\(\frac{n^2}{b}\)),
取 b=\(\frac{n}{\sqrt{m}}\)最优
时间复杂度为O(\(n\sqrt{m}\))。
增加操作
例题

过程
- 对原序列进行分块,对询问按以左端点所属块编号升序为第一关键字,右端点升序为第二关键字的方式排序。
- 按顺序处理询问:
- 如果询问左端点所属块 B 和上一个询问左端点所属块的不同,那么将莫队区间的左端点初始化为 B 的右端点加 1, 将莫队区间的右端点初始化为 B 的右端点;
- 如果询问的左右端点所属的块相同,那么直接扫描区间回答询问;
- 如果询问的左右端点所属的块不同:
- 如果询问的右端点大于莫队区间的右端点,那么不断扩展右端点直至莫队区间的右端点等于询问的右端点;
- 不断扩展莫队区间的左端点直至莫队区间的左端点等于询问的左端点;
- 回答询问;
撤销莫队区间左端点的改动,使莫队区间的左端点回滚到 B 的右端点加 1。
代码
#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[50010];
int L[300],R[300];//分块信息
int pos[50010],cnt;
struct jade
{
int id,l,r;
}q[50010];
int ls[50010],rs[50010],back_ls[50010],back_rs[50010];
//ls[x]和rs[x]分别表示x点向左向右延伸距离
//back_ls, back_rs用于后面的回滚
int num,ans[50010];
bool cmp(jade nod1,jade nod2)
{
int p=pos[nod1.l];
int q=pos[nod2.l];
if(p!=q)
{
return p<q;
}
return nod1.r<nod2.r;
}
void init()
{
int B=n/sqrt(m);
cnt=n/B;
for(int i=1;i<=cnt;i++)
{
L[i]=(i-1)*B+1;
R[i]=i*B;
}
if(R[cnt]<n)
{
cnt++;
L[cnt]=R[cnt-1]+1;
R[cnt]=n;
}
for(int i=1;i<=cnt;i++)
{
for(int j=L[i];j<=R[i];j++)
{
pos[j]=i;
}
}
}
void add(int x)
{
//更新x这个点的左右延伸距离
//如果x在某个连续区间的中间位置,可能会出现左延伸或右延伸不能更新,这种情况不影响答案
//因为我们求的是最大连续区间,所以只要保证当x为连续区间边界的点时,能够更新就可以
//因此,后面我们要更新rs[x-ls[x]+1]和ls[x+rs[x]-1]的值
ls[x]=ls[x-1]+1;//左边延伸+1
rs[x]=rs[x+1]+1;//右边延伸+1;
int t=ls[x]+rs[x]-1;
//更新该连续区间左右端点的延伸距离
rs[x-ls[x]+1]=t;
ls[x+rs[x]-1]=t;
num=max(num,t);
}
int main()
{
int x,y;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
for(int i=1;i<=m;i++)
{
cin>>x>>y;
q[i]={i,x,y};
}
init();
sort(q+1,q+1+m,cmp);
for(int i=1;i<=m;)
{
int j=i;
while(j<=m&&pos[q[i].l]==pos[q[j].l])
{
j++;
}
int right=R[pos[q[i].l]];
//块内移动,直接暴力
while(i<j&&q[i].r<=right)
{
num=0;
memset(ls,0,sizeof(ls));
memset(rs,0,sizeof(rs));
int id=q[i].id;
int l=q[i].l;
int r=q[i].r;
for(int k=l;k<=r;k++)
{
add(a[k]);
}
ans[q[i].id]=num;
i++;
}
//块外移动
//r设置为q[i].l所在块终点位置,然后向右移动
//l设置为r+1,即q[i].l所在块的下一个块的起始位置,以保证初始空间为0,然后向左移动
//r的轨迹会一直往后移(前面对q的排序)
//l会在q[i].l中不断来回移动
//每次求出一个询问后,回滚到l的起始位置
num=0;
memset(ls,0,sizeof(ls));
memset(rs,0,sizeof(rs));
int r=right,l=right+1;
while(i<j)
{
//先向右扩展
while(r<q[i].r)
{
r++;
add(a[r]);
}
int backup=num;//先备份下来,以便后面回滚,然后再向左扩展
memcpy(back_ls,ls,sizeof(ls));
memcpy(back_rs,rs,sizeof(rs));
while(l>q[i].l)
{
l--;
add(a[l]);
}
ans[q[i].id]=num;//回滚
l=right+1;
num=backup;
memcpy(ls,back_ls,sizeof(ls));
memcpy(rs,back_rs,sizeof(rs));
i++;
}
num=0;
memset(ls,0,sizeof(ls));
memset(rs,0,sizeof(rs));
}
for(int i=1;i<=m;i++)
{
cout<<ans[i]<<endl;
}
return 0;
}
附录
关于四个循环位置:
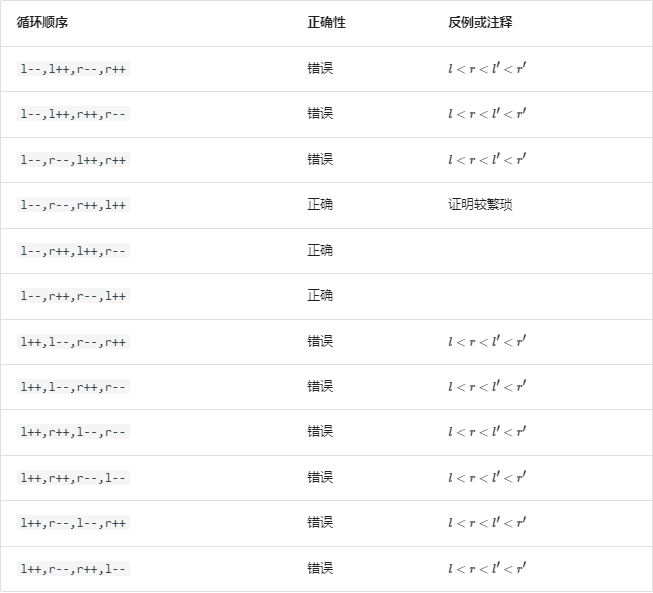
本文来自博客园,作者:BIxuan—玉寻,转载请注明原文链接:https://www.cnblogs.com/zhangyuxun100219/p/18973164



 浙公网安备 33010602011771号
浙公网安备 33010602011771号