树链剖分

如图

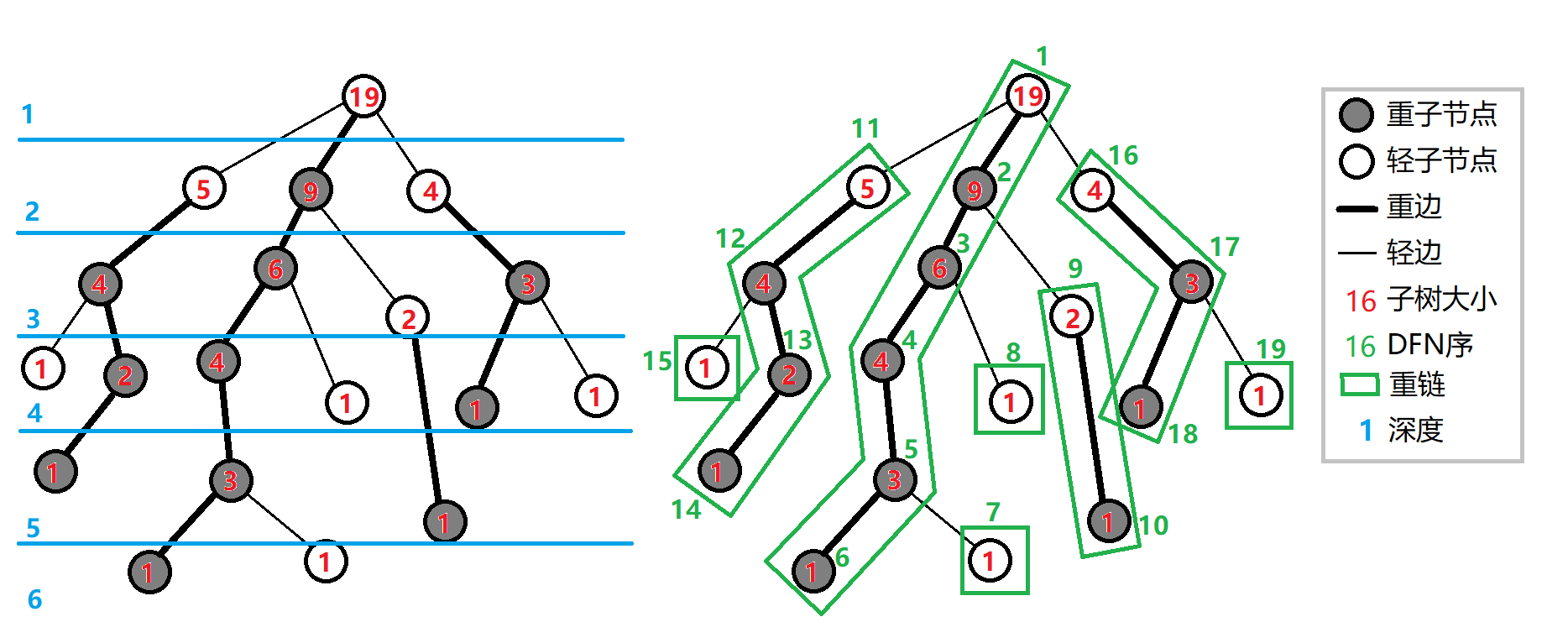
具体实现

• father[x] 表示节点x在树上的父亲

• deep[x]表示节点x在树上的深度

• size[x]表示节点x的子树的节点个数

• heavy_son[x]表示节点x的重儿子

• top[x]表示节点x所在重链的顶部节点（深度最小）

• dfn[x]表示节点x的dfs序，也是其在线段树中的编号

• rnk[x]表示dfs序所对应的节点编号，有rnk(dfn(x))=x

代码模版

#include<bits/stdc++.h>
using namespace std;
int a[100010]={};
struct xds
{
	int l,r,sum,tag; 
};
xds tree[400040];//线段树变量
int h[100010]={},nxt[200020]={},to[200020]={},tot=0;//邻接链表变量
int n=0,m=0,ro=0,p=0;//ro:根节点  p:模数
int father[100010]={},deep[100010]={},size[100010]={},heavy_son[100010]={},top[100010]={};//重链剖分变量
int dfn[100010]={},rnk[100010]={},cnt=0;//重链剖分变量 cnt 用来求dfs序
#define lson (root<<1)
#define rson (root<<1|1)
void pushup(int root)
{
	tree[root].sum=(tree[lson].sum+tree[rson].sum)%p;
}
void put_down_tag(int root)//把当前节点root的延迟标记下放到左右儿子
{
	if(tree[root].tag)
	{
		int tg=tree[root].tag;
		tree[lson].tag=(tree[lson].tag+tg)%p;
		tree[rson].tag=(tree[rson].tag+tg)%p;
		tree[lson].sum=(tree[lson].sum+tg*(tree[lson].r-tree[lson].l+1)%p)%p;
		tree[rson].sum=(tree[rson].sum+tg*(tree[rson].r-tree[rson].l+1)%p)%p;
		tree[root].tag=0;
	}
	return ;
}
//建树
//l和r对应的是dfn
void build(int root,int l,int r)
{
	tree[root].l=l;
	tree[root].r=r;
	if(l==r)
	{
		tree[root].sum=a[rnk[l]]%p;//l为dfn值，所以rnk[l]对应的是原来的点
		return ;
	}
	int mid=(l+r)>>1;
	build(lson,l,mid);
	build(rson,mid+1,r);
	pushup(root);
}
void add(int root,int l,int r,int val)
{

	if(l<=tree[root].l&&tree[root].r<=r)
	{
		tree[root].tag=(tree[root].tag+val)%p;
		tree[root].sum=(tree[root].sum+val*(tree[root].r-tree[root].l+1)%p)%p;
		return ;
	}
	put_down_tag(root);
	int mid=(tree[root].l+tree[root].r)>>1;
	if(l<=mid)
	{
		add(lson,l,r,val);
	}
	if(r>mid)
	{
		add(rson,l,r,val);
	}
	pushup(root);
	return ;
}
int find(int root,int l,int r)
{
	int res=0;
	if(l<=tree[root].l&&tree[root].r<=r)
	{
		return tree[root].sum%p;
	}
	put_down_tag(root);
	int mid = (tree[root].l+tree[root].r)>>1;
	if(l<=mid) 
	{
		res=(res+find(lson,l,r))%p;
	}
	if(r>mid)
	{
		res=(res+find(rson,l,r))%p;;
	} 
	return res;
}
void add_edge(int x,int y)
{
	tot++;
	to[tot]=y;
	nxt[tot]=h[x];
	h[x]=tot;
}
//线段树

 
//求出 father(x)，deep(x)，size(x)，heavy_son(x)
void dfs_first(int x)
{
	heavy_son[x]=-1;
	size[x]=1;
	for(int i=h[x];i;i=nxt[i])
	{
		int y=to[i];
		if(!deep[y]) 
		{
			deep[y]=deep[x]+1;
			father[y]=x;
			dfs_first(y);
			size[x]+=size[y];
			if(heavy_son[x]==-1||size[y]>size[heavy_son[x]])
			{
				heavy_son[x]=y;
			}
		}
	}
	return ;
}
//求出 top(x)，dfn(x)，rnk(x)
void dfs_second(int x,int x_top)
{
	top[x]=x_top;
	cnt++;
	dfn[x]=cnt;
	rnk[cnt]=x;
	if(heavy_son[x]==-1)//x为叶子节点
	{
		return ;
	}
	dfs_second(heavy_son[x],x_top);// 优先对重儿子进行 DFS，可以保证同一条重链上的点 DFS 序连续
	for(int i=h[x];i;i=nxt[i])
	{
		int y=to[i];
		if(y!=heavy_son[x]&&y!=father[x])	//y为轻儿子时，单独开一条链，y为链顶端点
		{
			dfs_second(y,y);
		}
	}
	return ;
}
void add_decomposition(int x,int y,int val)
{
	//跳重链
	while(top[x]!=top[y])
	{
		if(deep[top[x]]<deep[top[y]])
		{
			swap(x,y);
		}
		add(1,dfn[top[x]],dfn[x],val);
		x=father[top[x]];
	}
	//已跳到同一条重链
	if(deep[x]>deep[y])
	{
		swap(x,y);
	}
	add(1,dfn[x],dfn[y],val);
	return ;
}
int find_decomposition(int x,int y)
{
	int res=0;
	//跳重链
	while(top[x]!=top[y])
	{
		if(deep[top[x]]<deep[top[y]])
		{
			swap(x,y);
		}
		res=(res+find(1,dfn[top[x]],dfn[x]))%p;
		x=father[top[x]];
	}
	//已跳到同一条重链
	if(deep[x]>deep[y])
	{
		swap(x,y);
	}
	res=(res+find(1,dfn[x],dfn[y]))%p;
	return res;
}


//树链剖分 
int main()
{
	cin>>n>>m>>ro>>p;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	for(int i=1;i<n;i++)
	{
		int x,y;
		cin>>x>>y;
		add_edge(x,y);
		add_edge(y,x);
	}
	deep[ro]=1;
	//执行重链剖分,两遍 DFS 预处理出这些值，
	//第一次 DFS 求出 father(x)，deep(x)，size(x)，heavy_son(x) 
	dfs_first(ro);
	//第二次 DFS 求出 top(x)，dfn(x)，rnk(x)。
	dfs_second(ro,ro);
	//针对dfn序建树
	build(1,1,cnt);
	while(m--)
	{
		int way;
		cin>>way;
		if(way==1)
		{
			int x,y,z;
			cin>>x>>y>>z;
			add_decomposition(x,y,z);
		}
		if(way==2)
		{
			int x,y;
			cin>>x>>y;
			int ans=find_decomposition(x,y);
			cout<<ans<<endl; 
		}
		if(way==3)
		{
			int x,z;
			cin>>x>>z;
			add(1,dfn[x],dfn[x]+size[x]-1,z);
		}
		if(way==4)
		{
		    int x;
			cin>>x;
			int ans=find(1,dfn[x],dfn[x]+size[x]-1);
			cout<<ans<<endl;	
		}
	}
	return 0;
}

原题：洛谷P3384